6.4. Neuronske mreže#
Na kraju ovog poglavlja, pokažimo kako razne tehnike i ideje koje smo proučavali tijekom cijelog kolegija možemo upotrijebiti zajedno i njima motivirati jednu od danas najpopularnijih metoda strojnog učenja, a to su neuronske mreže.
Prisjetimo se ponovno problema prepoznavanja znamenki koji nam je poslužio kao primjer primjene problema najmanjih kvadrata. Na danoj slici razlučivosti \(P \times P\) pixela je prikazana neka dekadska znamenka, a naš zadatak je implementirati metodu koja će za takvu sliku odrediti o kojoj je znamenci riječ. Ranije smo pokazali da svaku takvu sliku možemo reprezentirati kao vektor \(x \in \R^n\), gdje je \(n = P^2\).
Promotrimo funkciju \(\Psi : \R^n \to \{0, 1, \ldots, 9\}\) koja svakoj takvoj slici pridružuje pripadnu znamenku. Ta funkcija očito postoji, no čini nam se posve nemoguće napisati matematičku formulu kojom bismo opisali takvo preslikavanje. Ono što možemo napraviti je pokušati pogoditi kojeg je oblika takva funkcija.
Pretpostavimo, na primjer, da funkcija \(\Psi\) ima vrlo jednostavni oblik:
Dakle, \(\Psi(x) = x^T \cdot \theta\), za neki nepoznati vektor \(\theta \in \R^n\).
Kako odrediti \(\theta\)? Korištenjem slika na kojima već znamo koje su znamenke na njima. Ovaj pristup zovemo nadzirano učenje (eng. supervised learning).
Dakle, imamo slike \(x_1, \ldots, x_N\) za koje znamo koje su znamenke \(y_1, \ldots, y_N\) na njima.
Takvih označenih primjera tipično imamo jako puno, tj. \(N \gg n\).
Trebalo bi vrijediti \(\Psi(x_i) = y_i\), za sve \(i=1, \ldots, N\), no zbog \(N \gg n\) i jer je naša \(\Psi\) samo aproksimacija „prave” će biti \(\Psi(x_i) \approx y_i\).
Stoga \(\theta\) određujemo tako da minimiziramo srednju kvadratnu grešku (eng. mean square error, MSE) na svim označenim primjerima (koje onda zovemo i podacima za treniranje)
\[ \min_{\theta} \frac{1}{N} \sum_{i = 1}^N (y_i - \Psi(x_i))^2. \]Stavimo \(A = \mb{c} x_1^T \\ x_2^T \\ \vdots \\ x_N^T \me\), \(b = \mb{c} y_1 \\ y_2 \\ \vdots \\ y_N \me\), \(x = \theta\).
Problem minimizacije srednje kvadratne greške se svodi na \(\min_x \|Ax - b\|\), tj. problem najmanjih kvadrata.
Upravo tako smo problem prepoznavanja znamenki riješili ranije.
Dakle, uz našu hipotezu da funkcija \(\Psi\) ima ovaj vrlo specijalni oblik, problem već znamo riješiti. Međutim, zašto bi funkcija \(\Psi\) imala taj oblik?
Mi unaprijed nemamo apsolutno nikakvu informaciju o tome kako \(\Psi(x)\) ovisi o \(x\), eventualno je razumna pretpostavka da je \(\Psi\) neprekidna ili glatka.
Funkcijama oblika \(x \mapsto x^T \cdot \theta\) ne možemo aproksimirati bilo koju neprekidnu funkciju \(\Psi\), nego samo linearne funkcije.
Stoga nam treba neki mehanizam koji nam omogućava da napravimo dobru aproksimaciju bilo koje (neprekidne?) funkcije \(\Psi\).
Rješenje će biti neuronske mreže: one će biti takvi univerzalni aproksimatori.
Univerzalna aproksimacija za \(\Psi : [a, b] \to \R\)
Uočite da u slučaju \(n=1\) i funkcija \(\Psi : [a, b] \to \R\) koje su klase \(C^1\) gornji problem možemo riješiti korištenjem npr. Čebiševljevih polinoma \(T_0, T_1, \ldots\).
Kako smo spomenuli u poglavlju o interpolaciji, svaka se funkcija \(\Psi\) klase \(C^1\) može po volji točno aproksimirati kao \(\Psi(x) \approx \sum_{i=0}^\ell \theta_i T_i(x)\) uz dovoljno veliki \(\ell\). Koeficijente \(\theta_i\) onda zaista možemo odrediti rješavanjem problema najmanjih kvadrata. No nije jasno kako ovaj pristup poopćiti na slučaj \(n > 1\).
Neuronske mreže: univerzalni aproksimatori#
Neka su \(W_0, W_1, \ldots, W_{\ell}\) matrice težina, a \(b_0, b_1, \ldots, b_{\ell}\) vektori pristranosti (eng. bias) odgovarajućih dimenzija, te neka su \(\sigma_0, \sigma_1, \ldots, \sigma_{\ell} : \R \to \R\) nelinearne aktivacijske funkcije.
Neuronska mreža \(NN\) preslikava ulazni vektor \(x\) u izlazni vektor \(y\) po sljedećoj formuli:
Aktivacijske funkcije se primjenjuju po komponentama vektora.
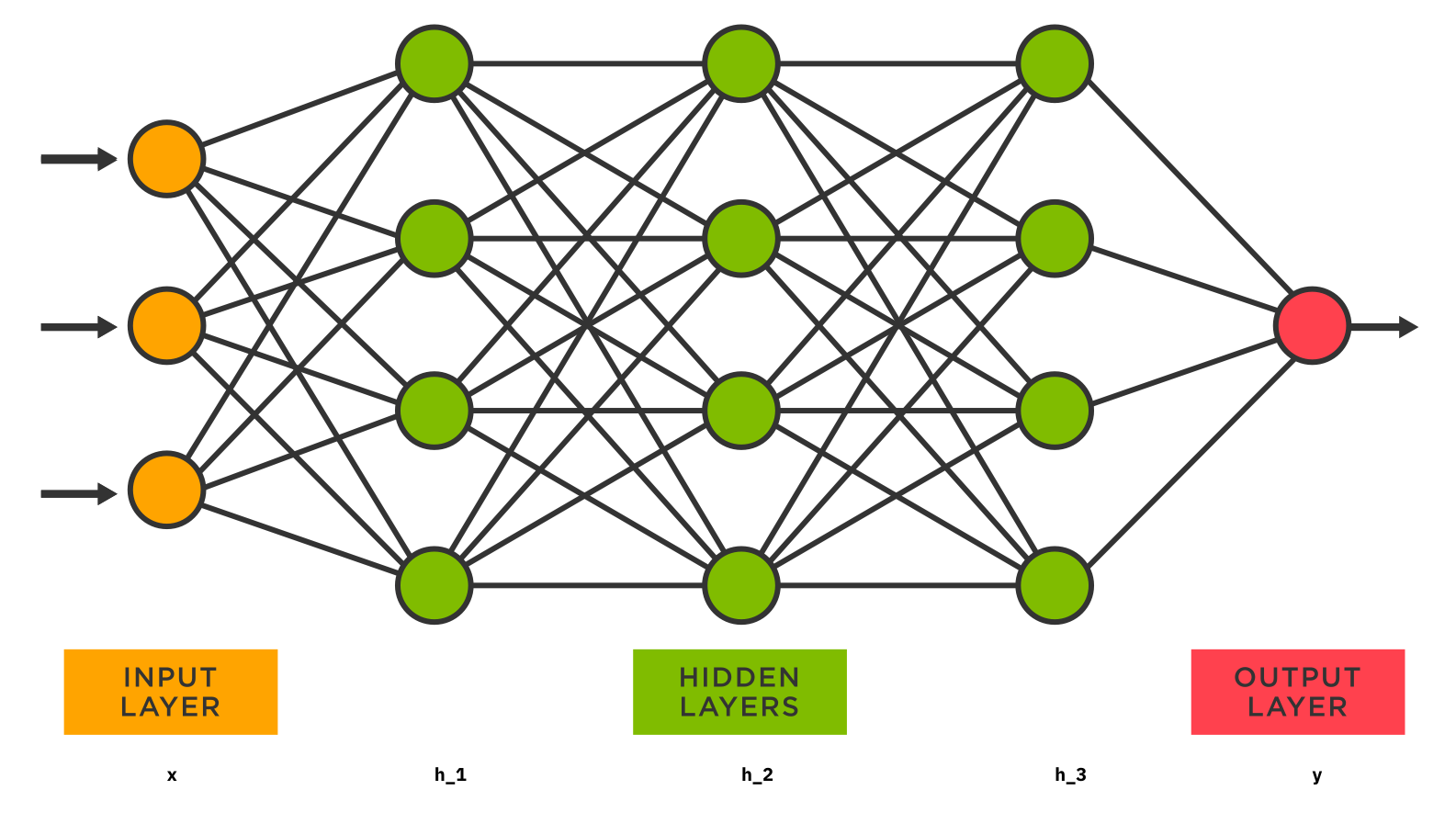
Komponente vektora \(x\) još zovemo ulazni sloj, vektora \(y\) izlazni sloj, a vektora \(h_1, \ldots, h_{\ell}\) skriveni slojevi.
Dimenziju vektora u nekom sloju nazivamo brojem neurona u tom sloju. Na slici gore, ulazni sloj ima 3 neurona, a prvi skriveni sloj 4 neurona.
Tipično, kod neuronskih mreža fiksiramo topologiju (broj slojeva, broj neurona po slojevima) i aktivacijske funkcije. Funkciju \(NN\) onda promatramo kao parametriziranu funkciju u kojoj smo slobodni odabrati matrice težina i vektore pristranosti.
Neuronska mreža je, dakle, nelinearna funkcija
Iz naše perspektive, cilj učenja neuronske mreže je odabrati parametre (matrice težina i vektore pristranosti) tako da \(NN\) bude aproksimacija neke funkcije \(\Psi : \R^n \to \R^m\).
Kao što smo raspravili ranije:
Funkcija \(\Psi\) tipično nije zadana eksplicitnom formulom.
Funkcija \(\Psi\) je tipično zadana nizom parova \((x_i, y_i)\) takvih da je \(y_i = \Psi(x_i)\) za \(i=1, 2, \ldots, N\).
Dokazano je da su neuronske mreže s dovoljno mnogo neurona univerzalni aproksimatori. Naime, vrijedi sljedeći teorem.
Neka je \(\sigma_0 : \R \to \R\) neprekidna funkcija koja nije polinom, \(K \subseteq \R^n\) kompaktan skup, te \(\Psi : K \to \R^m\) neprekidna funkcija.
Tada za svaki \(\eps > 0\) postoje \(k \in \N\), te \(W_0 \in \R^{k \times n}\), \(b_0 \in \R^k\), \(W_1 \in \R^{m \times k}\) takvi da je
pri čemu je \(NN(x) = W_1 \sigma_0 (W_0 x + b_0)\).
Drugim riječima, svaka neprekidna funkcija se po volji točno može aproksimirati neuronskom mrežom s jednim skrivenim slojem.
Postoje i druge varijante teorema koje npr. ograničavaju maksimalni broj neurona u slojevima na \(\max\{n+1, m\}\).
Radi jednostavnosti, u ovoj cjelini promatramo samo neuronske mreže s tzv. potpuno povezanim slojevima (eng. fully connected layers ili linear layers). Postoji i cijeli raspon drugih mogućnosti kojima se definira koji neuroni iz nekog sloja su povezani s kojim neuronima iz idućeg (ili čak nekog posve drugog) sloja.
Primjer: Prepoznavanje znamenki#
Vratimo se na problem prepoznavanja znamenki i riješimo ga korištenjem neuronske mreže. Ovog puta ćemo koristiti znamenke iz kolekcije MNIST. Svaka takva znamenka je spremljena u slici, odnosno, matrici dimenzija \(28 \times 28\). U kolekciji postoji \(60000\) označenih znamenki za treniranje i još \(10000\) za testiranje. Mi ćemo, radi kraćeg trajanja optimizacije, izdvojiti samo prvih \(4096\) znamenki za treniranje. Istreniranu mrežu ćemo provjeriti na prvih \(16\) testnih primjera.
import numpy as np;
import matplotlib.pyplot as plt;
# Podaci se nalaze u sklopu biblioteke tensorflow.
from tensorflow.keras.datasets import mnist;
from tensorflow.keras.utils import to_categorical;
# Učitamo cijelu kolekciju za treniranje i testiranje.
(x_train, y_train), (x_test, y_test) = mnist.load_data();
# Izdvojimo prvih 4096 podataka za treniranje i 16 za testiranje.
x_train = x_train[:4096]; y_train = y_train[:4096];
x_test = x_test[:16]; y_test = y_test[:16];
# Skaliramo slike tako da su u njima brojevi između 0 i 1.
x_train = x_train /255.0; x_test = x_test / 255.0;
# Nacrtajmo npr. 125. sliku iz podataka za treniranje.
# U y_train piše koja je to znamenka.
plt.imshow( x_train[125], cmap=plt.get_cmap('gray') );
plt.title( f'Na slici je znamenka {y_train[125]}' );
plt.show();
2025-03-02 19:35:02.809731: I tensorflow/core/util/port.cc:113] oneDNN custom operations are on. You may see slightly different numerical results due to floating-point round-off errors from different computation orders. To turn them off, set the environment variable `TF_ENABLE_ONEDNN_OPTS=0`.
2025-03-02 19:35:02.809943: I external/local_tsl/tsl/cuda/cudart_stub.cc:32] Could not find cuda drivers on your machine, GPU will not be used.
2025-03-02 19:35:02.812324: I external/local_tsl/tsl/cuda/cudart_stub.cc:32] Could not find cuda drivers on your machine, GPU will not be used.
2025-03-02 19:35:02.842293: I tensorflow/core/platform/cpu_feature_guard.cc:210] This TensorFlow binary is optimized to use available CPU instructions in performance-critical operations.
To enable the following instructions: AVX2 AVX512F AVX512_VNNI FMA, in other operations, rebuild TensorFlow with the appropriate compiler flags.
2025-03-02 19:35:03.363203: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Could not find TensorRT
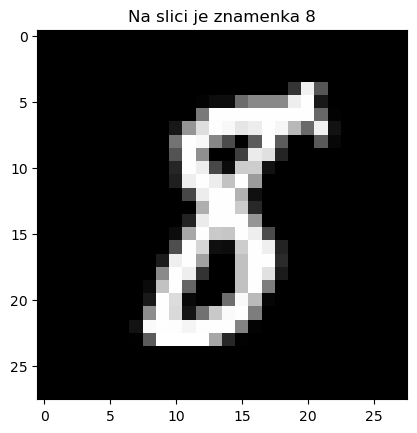
Svaka slika je matrica dimenzija \(28 \times 28\). Razmotajmo svaku tu matricu u vektor duljine \(28^2 = 784\). Spremimo sve podatke za treniranje u jednu matricu kojoj je svaki stupac jedan podatak, tj. svaki stupac te matrice predstavlja jednu sliku.
# x_train[i] je PxP matrica (P=28). Konvertiramo ih u vektore duljine n=P^2.
P = x_train[0].shape[0];
n = P*P;
# Razmotamo matrice u vektore.
x_train = x_train.reshape(-1, n);
x_test = x_test.reshape(-1, n);
# Još treba transponirati matricu (u kolekciji je svaki primjer jedan redak).
x_train = x_train.T;
x_test = x_test.T;
# Sada je svaka slika spremljena kao jedan stupac matrica x_train, x_test.
print( f'Dimenzije matrice x_train: {x_train.shape}' );
print( f'Dimenzije matrice x_test: {x_test.shape}' );
Dimenzije matrice x_train: (784, 4096)
Dimenzije matrice x_test: (784, 16)
Sada prelazimo na definiranje neuronske mreže. Umjesto da nastojimo aproksimirati funkciju \(\Sigma : \R^{784} \to \R\) koja slici znamenke pridružuje jedan broj (tu znamenku), logičnije je pokušati aproksimirati funkciju \(\Psi : \R^{784} \to \R^{10}\) koja slici znamenke pridružuje vektor \(p \in \R^{10}\).
Ideja je da \(p_i\) daje vjerojatnost da se na slici nalazi znamenka \(i\).
Često je slučaj da su npr. slike znamenki \(3\) i \(8\) relativno slične. Na primjer, malom promjenom slike na kojoj je znamenka \(3\) možemo dobiti sliku na kojoj je znamenka \(8\).
Vidimo da stoga ne možemo očekivati da je funkcija \(\Sigma\) neprekidna.
S druge strane, posve je prirodno očekivati da je funkcija \(\Psi\) neprekidna: za slike na kojima je očito znamenka \(3\) će biti \(p_3 \approx 1\), za one na kojima je očito znamenka \(8\) će biti \(p_8 \approx 1\), a za one za koje nismo sigurni će biti \(p_3 \approx p_8 \approx 0.5\).
Pretvorimo polja y_train i y_test u kojima piše koja je znamenka na slici u vektore iz \(\R^{10}\). Na primjer, za znamenku \(8\) ćemo napraviti vektor \((0, 0, 0, 0, 0, 0, 0, 0, 1, 0)\) (prva komponenta vektora odgovara vjerojatnosti da je na slici znamenka \(0\)).
# y_train[i] je znamenka. Konvertiramo ju u vektor duljine 10,
# oblika [0, 0, 0, 0, 0, 0, 0, 1, 0, 0].
# U tensorflow-u postoji funkcija koja će to napraviti za nas.
y_train = to_categorical(y_train);
y_test = to_categorical(y_test);
# y_train i y_test su sada matrice. Opet ih treba transponirati da je
# jedan primjer = jedan stupac (a ne jedan redak).
y_train = y_train.T;
y_test = y_test.T;
# 125. znamenka u trening podacima je bila znamenka 8:
print( y_train[:, 125] );
[0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]
Sada ćemo definirati neuronsku mrežu \(NN : \R^{784} \to \R^{10}\) kojom ćemo htjeti postići \(NN(x) \approx \Psi(x)\). Naša neuronska mreža će imati samo jedan skriveni sloj sa \(128\) neurona. Aktivacijska funkcija nakon svakog sloja će biti tzv. sigmoid:
Dakle, preslikavanje \(NN\) će biti definirano sa
Uočite da je slika funkcije \(\sigma\) skup \(\langle 0, 1 \rangle\), pa će u tom skupu biti i sve komponente izlaznog vektora \(NN(x)\).
Parametri koje trebamo odrediti su elementi matrica težina \(W_1 \in \R^{128 \times 784}\) i \(W_2 \in \R^{10 \times 128}\), te elementi vektora pristranosti \(b_1 \in \R^{128}\) i \(b_2 \in \R^{10}\).
Dakle, funkcija \(NN\) ovisi o ukupno \(128 \cdot 784 + 10 \cdot 128 + 128 + 10 = 101770\) parametara čije vrijednosti trebamo odabrati.
Postavimo na početku te vrijednosti (manje-više) slučajno.
Kasnije ćemo minimizirati neku funkciju po svim mogućim izborima tih parametara, pa u skladu s notacijom iz prethodne cjeline o optimizaciji, sve te parametre zajedno označimo sa \(\theta\). Dakle, možemo zamišljati da je \(\theta \in \R^{101770}\).
def sigmoid( x ):
# Aktivacijska funkcija.
return 1 / (1 + np.exp(-x));
def NN( W1, b1, W2, b2, x ):
# Neuronska mreža s jednim skrivenim slojem.
x = sigmoid( W1 @ x + b1 );
x = sigmoid( W2 @ x + b2 );
return x;
# Početne, slučajne vrijednosti parametara W1, b1, W2, b2.
# Inicijalni parametri naše neuronske mreže s jednim skrivenim slojem od 128 neurona.
# Ranije smo već postavili n = 784.
W1 = np.random.randn(128, n) / np.sqrt(n/2); # Slučajna matrica dimenzija 128 x 784.
b1 = np.zeros((128, 1)); # Nul-vektor dimenzije 128.
W2 = np.random.randn(10, 128) / np.sqrt(128/2); # Slučajna matrica dimenzija 10 x 128.
b2 = np.zeros((10, 1)); # Nul-vektor dimenzije 10.
Provjerimo kako neuronska mreža predviđa koje se znamenke nalaze na testnim slikama prije treniranja. Možda imamo jako puno sreće i uopće ne treba trenirati mrežu i prilagođavati parametre :)
# Pogledajmo svih 16 slika iz testnog skupa i što NN kaže da je na njima.
y_NN = NN( W1, b1, W2, b2, x_test );
# Ispišimo vektor "vjerojatnosti" samo za prvu sliku.
print( 'Vektor vjerojatnosti za prvi testni primjer: ' );
print( y_NN[:, 0] );
print( '' );
# NN kaže da je na slici ona znamenka za koju je najveća "vjerojatnost".
znamenka_NN = np.argmax( y_NN[:, 0] );
print( f'NN predviđa da je na slici znamenka: {znamenka_NN}' )
# Zapravo je na slici ona znamenka gdje piše 1 u vektoru y_test.
znamenka_zapravo = np.argmax( y_test[:, 0] );
print( f'Zapravo je na slici znamenka: {znamenka_zapravo}' )
Vektor vjerojatnosti za prvi testni primjer:
[0.47588787 0.62811438 0.56604272 0.53980161 0.52412345 0.50055091
0.68787484 0.44174841 0.44224856 0.52644696]
NN predviđa da je na slici znamenka: 6
Zapravo je na slici znamenka: 7
Vidimo da je mreža vrlo „nesigurna” oko toga koja bi znamenka mogla biti na slici; u vektoru vjerojatnosti na svim indexima piše dosta velik broj, zapravo posve slučajno određen.
Sada prelazimo na treniranje neuronske mreže. Želimo odrediti parametre \(W_1\), \(b_1\), \(W_2\), \(b_2\) tako da za trening podatke x_train mreža na izlazu daje vektore y_train. To možemo formulirati kao problem minimizacije funkcije
gdje su \((x_i, y_i)\), \(i=1, \ldots, N\) podaci iz trening seta (\(N=4096\)), a \(\theta\) parametri neuronske mreže. Ovaj problem se čini nevjerojatno težak: moramo pronaći optimalni vektor \(\theta_{\ast}\) iz prostora dimenzije čak \(101770\)! Pokušajmo primijeniti metode optimizacije koje smo naučili u prethodnoj cjelini.
Implementirajmo u Pythonu prvo funkciju \(f\) koju želimo optimizirati. Funkcija osim parametara po kojima treba raditi minimizaciju prima matricu x čiji su stupci podaci za treniranje, te matricu y čiji stupci su željeni izlazi (\(y_i = \Psi(x_i)\)).
def f( W1, b1, W2, b2, x, y ):
N = x.shape[1];
greske = y - NN( W1, b1, W2, b2, x );
norme_gresaka = np.linalg.norm( greske, axis=0 );
kvadrati_normi_gresaka = norme_gresaka ** 2;
srednja_kvadratna_greska = np.sum( kvadrati_normi_gresaka ) / N;
return srednja_kvadratna_greska;
Funkciju ćemo minimizirati korištenjem metode stohastičkog gradijentnog spusta s grupama. Za tu metodu nam treba gradijent funkcije \(f\) po svim parametrima optimizacije. Drugim riječima, moramo naći formule za sve parcijalne derivacije
funkcije \(f\) po svakom pojedinom elementu matrica \(W_1\), \(W_2\) i vektora \(b_1\), \(b_2\). To se može napraviti relativno jednostavno korištenjem pravila za derivaciju kompozicije, no nećemo ulaziti u objašnjenje. Zadatak za naprednije studente: pokušajte sami izvesti formule za ove derivacije ili dokazati da funkcija grad_f implementirana ispod to radi ispravno; pogledajte i članak o tzv. propagaciji unatrag.
def d_sigmoid( x ):
# Derivacija funkcije sigmoid u točki x.
sig_x = sigmoid(x);
return sig_x * (1.0 - sig_x);
def grad_f( W1, b1, W2, b2, x, y ):
# Vraća gradijent funkcije f po parametrima W1, b1, W2, b2 za svaki sloj.
# Na izlazu, u (grad_W1)_ij piše parcijalna derivacija funkcije f po elementu (W1)_ij.
# Analogno za grad_b1, grad_W2, grad_b2.
# Pokušajte dokazati da donji kod zaista ispravno izračuna gradijente!
# Zamislite za početak da matrice x i y imaju samo 1 stupac, tj. N = 1.
# x -> l1=W1*x+b1 -> l2=sigmoid(l1) -> l3=W2*l2+b2 -> l4=sigmoid(l3) -> g=||l4-y||^2.
l1 = W1 @ x + b1; # 128 x N
l2 = sigmoid( l1 ); # 128 x N
l3 = W2 @ l2 + b2; # 10 x N
l4 = sigmoid( l3 ); # 10 x N
# grad_var = gradijent funkcije g(x) = ||l4-y||^2 po varijabli var
# Koristimo formulu za derivaciju kompozicije, idemo unazad ("back propagation").
grad_l4 = 2*(l4 - y); # jer g(l4) = ||y-l4||^2 -> 10 x N (bez sumiranja!)
grad_l3 = grad_l4 * d_sigmoid(l3); # jer l4(l3) = sigmoid(l3) -> 10 x N
grad_l2 = W2.T @ grad_l3; # jer l3(l2) = W2*l2+b2 -> 128 x N
grad_l1 = grad_l2 * d_sigmoid(l1); # jer l2(l1) = sigmoid(l1) -> 128 x N
# Sada za W1, b1, W2, b2 računamo sume po svih N uzoraka.
grad_W2 = grad_l3 @ l2.T; # jer l3(W2) = W2*l2+b2 -> 10 x 128
grad_b2 = np.sum( grad_l3, axis=1, keepdims=True ); # jer l3(b2) = W2*l2+b2 -> 10 x 1; suma svih stupaca
grad_W1 = grad_l1 @ x.T; # jer l1(W1) = W1*x+b1 -> 128 x 784
grad_b1 = np.sum( grad_l1, axis=1, keepdims=True ); # jer l1(b1) = W1*x+b1 -> 128 x 1; suma svih stupaca
N = x.shape[1];
return (1.0/N * grad_W1, 1.0/N * grad_b1, 1.0/N * grad_W2, 1.0/N * grad_b2);
Sada napokon možemo prijeći na optimizaciju. Koristimo potpuno istu metodu stohastičkog gradijentnog spusta s grupama kako smo ju implementirali u prethodnoj cjelini. Jedina razlika je što su nam sada parametri optimizacije razdvojeni u 4 varijable.
Show code cell source
def stoh_grad_spust_s_grupama(
x, y, f, grad_f,
W1, b1, W2, b2,
eta, n_epoch, velicina_grupe ):
# Ulaz:
# x = polje točaka u kojima su vršena mjerenja, duljine N
# y = polje izmjerenih vrijednosti za svaku točku iz x
# f = funkcija cilja
# grad_f = gradijent funkcije cilja
# theta_W1, ..., theta_b2 = početne vrijednosti parametara
# eta = (konstantni) korak u metodi gradijentnog spusta
# n_epoch = broj epoha koje treba provesti.
# velicina_grupe = broj mjerenja koji sudjeluju u jednom koraku gradijentne metode.
# Izlaz:
# theta = vrijednost parametara nakon n_epoch epoha stoh. grad. spusta s grupama.
# hist = polje vrijednosti funkcije cilja nakon svakog koraka stog. grad. spusta s grupama. Samo za crtanje grafa.
# Broj mjerenja.
N = x.shape[1];
# Prazno polje hist.
hist = [];
# Iteracije.
for epoch in range( 0, n_epoch ):
# Napravi slučajnu permutaciju ulaznih podataka = stupaca od x i y.
perm = np.random.permutation( N );
x_perm = x[:, perm];
y_perm = y[:, perm];
for prvi_index in range( 0, N, velicina_grupe ):
# Grupa se sastoji od indexa prvi_index, prvi_index+1, ..., zadnji_index-1.
zadnji_index = min( N, prvi_index + velicina_grupe );
# Izračunaj gradijent funkcije f = 1/velicina_grupe * suma_{i u grupi} g(theta, xperm_i, yperm_i).
# Uoči: grad_f to zna napraviti i za grupu, a ne samo za sve podatka!
(grad_W1, grad_b1, grad_W2, grad_b2) = grad_f(
W1, b1, W2, b2,
x_perm[:, prvi_index:zadnji_index], y_perm[:, prvi_index:zadnji_index] );
# Zadnja grupa može biti manja.
velicina_ove_grupe = zadnji_index - prvi_index;
# Iduća iteracija parametara: stohastički gradijentni spust s grupama.
# theta = theta - eta * grad; (veličina grupe je uključena u grad)
W1 = W1 - eta * grad_W1;
b1 = b1 - eta * grad_b1;
W2 = W2 - eta * grad_W2;
b2 = b2 - eta * grad_b2;
# Spremimo trenutnu vrijednost funkcije cilja u polje hist.
hist.append( f(W1, b1, W2, b2, x, y) );
# Svakih 50 epoha ispišemo tren. vrijednost funkcije cilja.
if( epoch % 50 == 0 ):
print( f'Epoha {epoch:3d} -> f(theta) = {hist[-1]:.10f}' );
# Vratimo optimizirane vrijednosti parametara.
return (W1, b1, W2, b2, hist);
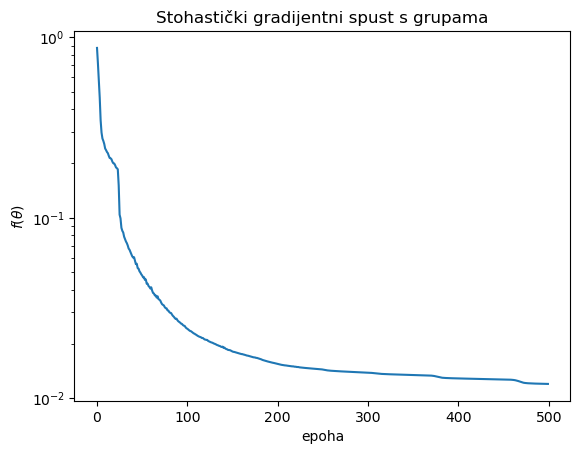
Pokrenemo optimizaciju funkcije \(f\). Koristimo korak \(\eta = 1.0\) i grupe veličine \(64\). Stajemo nakon \(500\) epoha. Ova faza može potrajati i nekoliko minuta, ovisno o brzini računala.
# Stoh. grad. spust s grupama veličine 64, eta = 1.0.
(W1, b1, W2, b2, hist) = stoh_grad_spust_s_grupama(
x_train, y_train, f, grad_f,
W1, b1, W2, b2,
1.0, 500, 64 );
Epoha 0 -> f(theta) = 0.9806168532
Epoha 50 -> f(theta) = 0.0449391656
Epoha 100 -> f(theta) = 0.0224473860
Epoha 150 -> f(theta) = 0.0161023600
Epoha 200 -> f(theta) = 0.0132895403
Epoha 250 -> f(theta) = 0.0113354620
Epoha 300 -> f(theta) = 0.0101739517
Epoha 350 -> f(theta) = 0.0091083555
Epoha 400 -> f(theta) = 0.0087355454
Epoha 450 -> f(theta) = 0.0081885188
Vidimo da je vrijednost funkcije cilja osjetno pala. Nacrtajmo i graf koji prikazuje kako se ona mijenjala kroz epohe.
plt.semilogy( hist );
plt.xlabel( 'epoha' );
plt.ylabel( '$f(\\theta)$' );
plt.title( 'Stohastički gradijentni spust s grupama' );
Pogledajmo sada može li istrenirana neuronska mreža predvidjeti znamenke s testnih slika. Uočite da te slike mreža nije vidjela prilikom treniranja.
# Pogledajmo svih 16 slika iz testnog skupa i što NN kaže da je na njima.
y_NN = NN( W1, b1, W2, b2, x_test );
# Ispišimo vektor "vjerojatnosti" samo za prvu sliku.
print( 'Vektor vjerojatnosti za prvi testni primjer: ' );
print( y_NN[:, 0] );
print( '' );
# NN kaže da je na slici ona znamenka za koju je najveća "vjerojatnost".
znamenka_NN = np.argmax( y_NN[:, 0] );
print( f'NN predviđa da je na slici znamenka: {znamenka_NN}' )
# Zapravo je na slici ona znamenka gdje piše 1 u vektoru y_test.
znamenka_zapravo = np.argmax( y_test[:, 0] );
print( f'Zapravo je na slici znamenka: {znamenka_zapravo}' )
Vektor vjerojatnosti za prvi testni primjer:
[1.10328292e-06 2.83223053e-09 4.14203754e-04 6.59650019e-04
6.84359529e-08 2.06451566e-05 5.30295194e-11 9.99772730e-01
1.19651806e-05 4.82445683e-06]
NN predviđa da je na slici znamenka: 7
Zapravo je na slici znamenka: 7
Sada su svi elementi vektora koji vrati \(NN(x)\) jako maleni, osim onog koji odgovara znamenci \(7\), a taj je vrlo blizu \(1\)! Neuronska mreža je sasvim sigurna da je na slici znamenka \(7\). Provjerimo što je i s ostalim primjerima iz testnog skupa.
Show code cell source
# Pogledajmo svih 16 slika iz testnog skupa i što NN kaže da je na njima.
y_NN = NN( W1, b1, W2, b2, x_test );
# Grafički prikaz.
fig = plt.figure(figsize=[16, 16]);
for i in range( 0, 16 ):
znamenka_NN = np.argmax( y_NN[:, i] );
znamenka_zapravo = np.argmax( y_test[:, i] );
# Nacrtaj sliku znamenke i ispiši predviđanje NN i koja je to znamenka zapravo.
ax1 = fig.add_subplot(4, 4, i+1);
ax1.title.set_text( f'NN: {znamenka_NN}, zapravo: {znamenka_zapravo}' );
ax1.imshow( x_test[:, i].reshape(28, 28), cmap='gray' );
Vidimo da je istrenirana mreža točno prepoznala sve znamenke iz testnog skupa osim jedne (za koju zapravo nije ni jasno je li na njoj \(5\) ili \(6\)). Metodom gradijentnog spusta uspjeli smo riješiti problem optimizacije u prostoru dimenzije \(101770\)!