Uvjetovanost

Sadržaj

1.4. Uvjetovanost#

Pretpostavimo ponovno da nekim algoritmom želimo izračunati \(y=f(x)\). Kao što smo vidjeli ranije:

Ako su podaci \(x\) došli nekim mjerenjem koje ima neku grešku, čak i korištenjem egzaktne aritmetike ćemo zapravo izračunati \(\tilde{y} = f(\tilde{x})\) za neki \(\tilde{x} \approx x\).
Rezultat \(\tilde{y}\) dobiven u konačnoj aritmetici računala možemo prikazati korištenjem greške unatrag: \(\tilde{y} = f(\tilde{x})\) za neki \(\tilde{x} \approx x\).

Prirodno pitanje koje se sada postavlja je sljedeće:

Uvjetovanost (intuitivno)

Ako znamo koliko su „blizu” ulazni podaci \(x\) i \(\tilde{x}\), možemo li ocijeniti koliko su „blizu” rezultati \(y=f(x)\) i \(\tilde{y}=f(\tilde{x})\)?

Ako je „udaljenost” \(f(x)\) i \(f(\tilde{x})\) puno veća nego „udaljenost” \(x\) i \(\tilde{x}\), reći ćemo da \(f\) ima veliku uvjetovanost ili da je loše uvjetovana. U protivnom je \(f\) dobro uvjetovana.

\[ \text{greška u rezultatu} \lesssim \red{\text{uvjetovanost}} \cdot \text{greška u podacima} \]

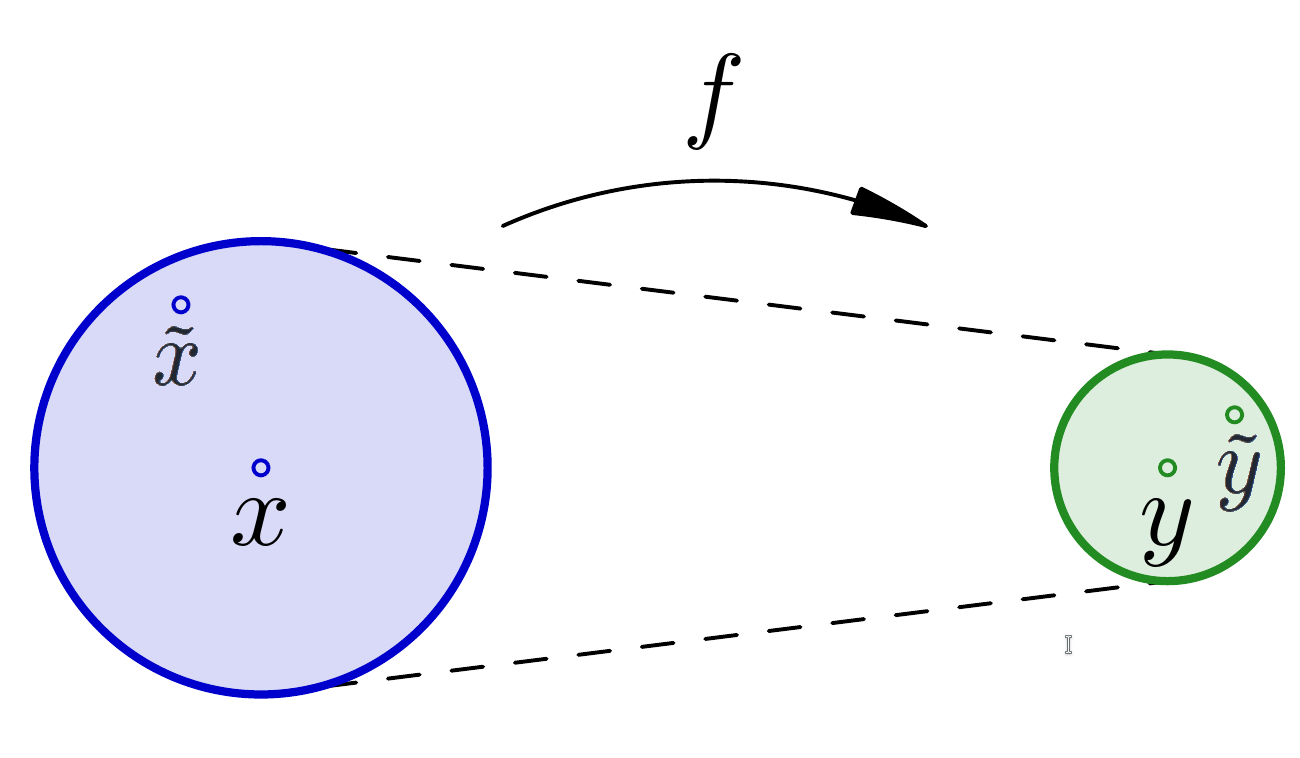
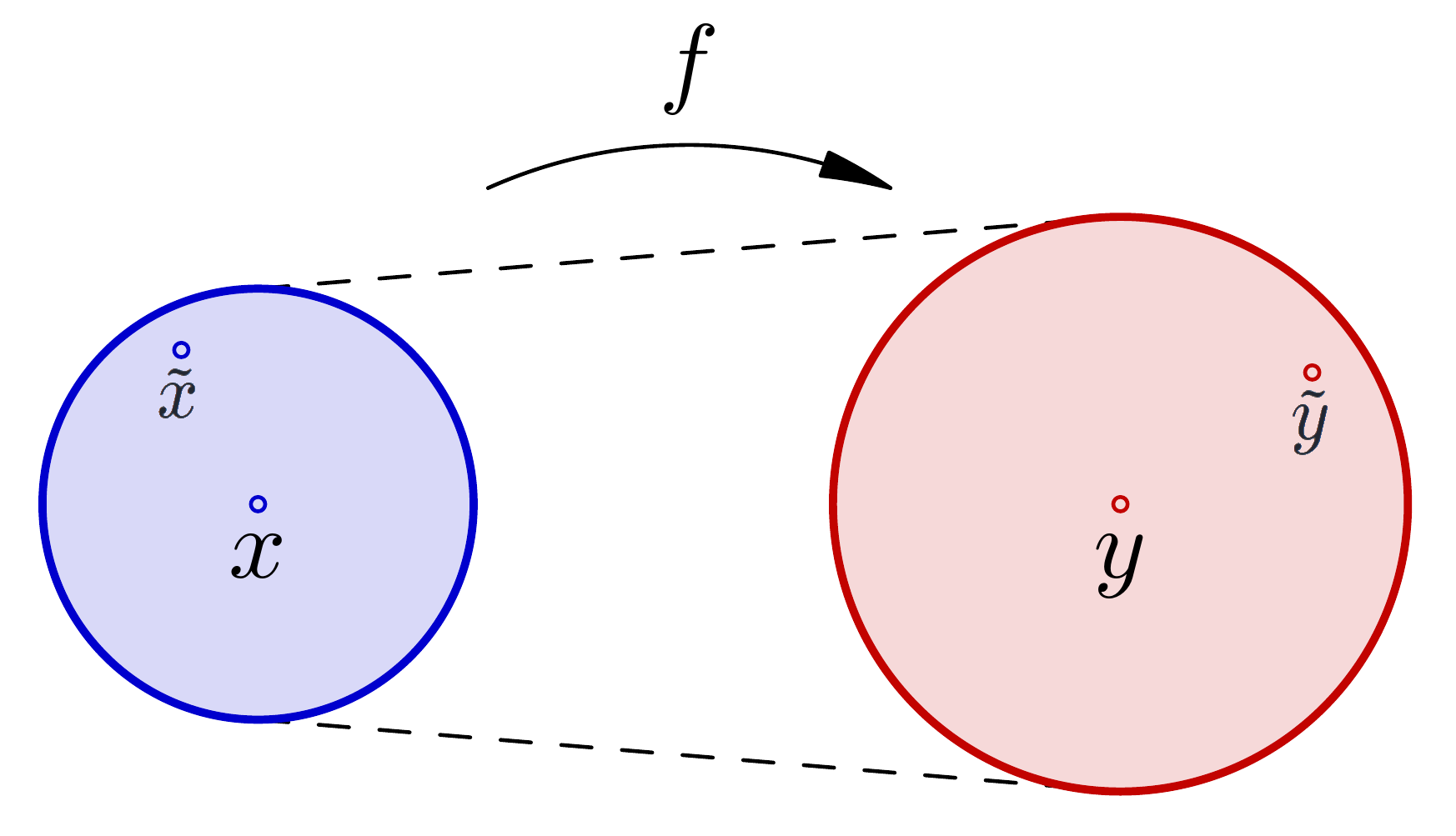
Na slici lijevo, funkcija \(f\) ima malu uvjetovanost i ona je „prigušivač” grešaka. Na slici desno, funkcija \(f\) ima veliku uvjetovanost i ona je „pojačalo” grešaka. Uvjetovanost funkcije \(f\) u točki \(x\) je omjer radijusa kruga oko \(y\) i radijusa kruga oko \(x\).

Svrha određivanja uvjetovanosti je dati odgovor na sljedeće pitanje:

Koju točnost rezultata možemo očekivati pri točnom računanju, bez grešaka zaokruživanja, s malo „pomaknutim”, netočnim podacima?

Ako za neki algoritam koji na računalu implementira funkciju \(f\) napravimo analizu grešaka unatrag (=greška u podacima) i znamo kolika je uvjetovanost funkcije \(f\), ovaj pristup nam automatski daje procjenu kolika je greška unaprijed (=greška u rezultatu)!

Uočite da pitanje uvjetovanosti ovisi isključivo o funkciji \(f\), a ne i o algoritmu koji koristimo za implementaciju \(f\). Algoritam kojim računamo \(f\) će utjecati isključivo na veličinu povratne greške (udaljenost \(x\) i \(\tilde{x}\))!

Određivanjem uvjetovanosti, tj. ovisnosti rješenja o greškama ili perturbacijama ulaznih podataka bavi se teorija perturbacija. Da bi gornja definicija postala precizna, moramo prvo objasniti kako mjeriti „udaljenost”. Ako su podaci neki realni brojevi, „udaljenost” \(x\) i \(\tilde{x}\) prirodno mjerimo apsolutnom greškom \(|x - \tilde{x}|\) ili relativnom greškom \(\frac{|x - \tilde{x}|}{|x|}\). Najčešće su podaci \(x\) ipak složeniji, na primjer, vektori ili matrice.

Napomena

Funkcije \(f\) koje ovdje promatramo mogu biti relativno komplicirane.

Na primjer, za matricu \(A\) i vektor \(b\) promatramo funkciju koja im pridružuje rješenje linearnog sustava \(Ax=b\), odnosno, \(f(A, b) = A^{-1}b\).

Ili, ako je \(A=LU\) LU-faktorizacija matrice \(A\), promatramo funkcije \(f_L(A) = L\), \(f_U(A) = U\).

Vektorske i matrične norme#

„Udaljenost” vektora i matrica prirodno je mjeriti pomoću norme njihove razlike. Podsjetimo se pojmova vektorske i matrične norme iz linearne algebre.

Definicija 1.14 (Vektorska norma)

Neka je \(V\) vektorski prostor nad poljem \(F\), gdje je \(F=\R\) ili \(F=\mathbb{C}\). Vektorska norma je funkcija \(\|\cdot\| : V \to \R\) takva da vrijedi:

\(\|x\| \geq 0\), za sve \(x \in V\), pri čemu jednakost vrijedi akko je \(x = 0\).
\(\|\alpha x\| = |\alpha| \|x\|\), za sve \(\alpha \in F\) i sve \(x \in V\).
\(\|x + y\| \leq \|x\| + \|y\|\), za sve \(x, y \in V\) (nejednakost trokuta).

Najčešće ćemo koristiti ove vektorske norme na prostorima \(V=\R^n\) ili \(V=\C^n\):

1-norma ili \(\ell_1\)-norma: \(\|x\|_1 := \sum_{i=1}^n |x_i|\).
2-norma ili \(\ell_2\)-norma ili euklidska norma: \(\|x\|_2 := \sqrt{\sum_{i=1}^n |x_i|^2}\).
\(\infty\)-norma ili \(\ell_\infty\)-norma: \(\|x\|_\infty := \max_{i=1, \ldots, n} |x_i|\).

Samo je 2-norma izvedena iz skalarnog produkta \(\langle x, y \rangle = \sum_{i=1}^n x_i \overline{y}_i\), pa je \(\|x\|_2 = \sqrt{ \langle x, x \rangle }\).

Prisjetimo se i ovog teorema iz linearne algebre.

Teorem 1.15 (Ekvivalentnost normi)

Ako je \(V\) konačno-dimenzionalan vektorski prostor, onda su sve norme na \(V\) ekvivalentne, tj. za svake dvije norme \(\|\cdot\|_a\) i \(\|\cdot\|_b\) postoje konstante \(m\) i \(M\) takve da za sve \(v \in V\) vrijedi

\[ m \|v\|_a \leq \|v\|_b \leq M \|v\|_a. \]

Na primjer, za sve \(x \in \R^n\) vrijedi:

\[ \|x\|_\infty \leq \|x\|_2 \leq \sqrt{n} \|x\|_\infty. \]

U praksi nije svejedno koju normu koristimo ako je \(n\) velik.

Zanimat će nas i prostori funkcija koji nisu konačno-dimenzionalni. Na prostoru \(C([a, b])\) svih neprekidnih funkcija \(f\) na segmentu \([a, b]\) možemo definirati ove norme:

\(L_1\)-norma: \(\|f\|_1 := \int_a^b |f(t)| dt\).
\(L_2\)-norma: \(\|f\|_2 := \left( \int_a^b |f(t)|^2 dt \right)^{1/2}\).
\(L_\infty\)-norma: \(\|f\|_\infty := \max_{t \in [a, b]} |f(t)|\).

Skup svih matrica fiksne dimenzije također čini vektorski prostor, pa se definicija matrične norme zapravo podudara s definicijom vektorske norme. Kod matričnih normi obično postavljamo i jedan dodatni zahtjev - konzistentnost.

Definicija 1.16 (Matrična norma)

Matrična norma je funkcija \(\|\cdot\| : \C^{m \times n} \to \R\) takva da vrijedi:

\(\|A\| \geq 0\), za sve \(A \in \C^{m \times n}\), pri čemu jednakost vrijedi akko je \(A = 0\).
\(\|\alpha A\| = |\alpha| \|A\|\), za sve \(\alpha \in \C\) i sve \(A \in \C^{m \times n}\).
\(\|A + B\| \leq \|A\| + \|B\|\), za sve \(A, B \in \C^{m \times n}\).

Dodatno, matrična norma je konzistentna ako vrijedi

\(\|AB\| \leq \|A\| \|B\|\), kad god je produkt \(AB\) definiran.

Ako stupce matrice reda \(m \times n\) naslažemo jedan na drugi, dobit ćemo vektor duljine \(mn\); ako promotrimo euklidsku normu tog vektora, dobivamo tzv. Frobeniusovu ili Hilbert-Schmidtovu matričnu normu:

\[ \|A\|_F = \sqrt{ \sum_{i=1}^m \sum_{j=1}^n |a_{ij}|^2} = (\text{tr}(A^\ast A))^{1/2}. \]

Drugi način kako možemo dobiti matričnu normu iz vektorske su tzv. operatorske norme: ako je \(\|\cdot\|\) vektorska norma, onda definiramo

\[ \|A\| := \max_{x \neq 0} \frac{\|Ax\|}{\|x\|} = \max_{\|x\|=1} \|Ax\|. \]

Primjeri često korištenih operatorskih normi su:

matrična 1-norma („maksimalna stupčana norma”):

\[ \|A\|_1 = \max_{j = 1, \ldots, n} \sum_{i=1}^m |a_{ij}|. \]

matrična 2-norma ili spektralna norma:

\[ \|A\|_2 = \sqrt{\lam_{\max}(A^\ast A)} = \sigma_{\max}(A).\]

Ovdje je sa \(\lam_{\max}(X)\) najveća svojstvena vrijednost matrice \(X\), a sa \(\sigma_{\max}(X)\) najveća singularna vrijednost matrice \(X\) (više o tome nešto kasnije).
matrična \(\infty\)-norma („maksimalna retčana norma”):

\[ \|A\|_\infty = \max_{i = 1, \ldots, m} \sum_{j=1}^n |a_{ij}|. \]

Napomena

Napomenimo da gornje relacije za \(\|A\|_1\), \(\|A\|_2\) i \(\|A\|_\infty\) nisu definicije tih normi. Definicija slijedi kao i definicija svih ostalih operatorskih normi (izvedene su iz odgovarajuće vektorske norme), dok su gornjim relacijama dani rezultati kako se te definicije mogu jednostavnije iskazati u tim slučajevima.

Sumirajmo neka važna svojstva matričnih normi.

Propozicija 1.17 (Svojstva matričnih normi)

Za matrične norme vrijede sljedeća svojstva:

Za svaku operatorsku normu vrijedi \(\|Ax\| \leq \|A\| \cdot \|x\|\), za sve matrice \(A\) i vektore \(x\).
Frobeniusova norma i sve operatorske norme su konzistentne.
Spektralna i Frobeniusova norma su unitarno invarijantne: za sve unitarne matrice \(U \in \C^{m \times m}\), \(V \in \C^{n \times n}\) i sve matrice \(A \in \C^{m \times n}\) vrijedi:

\[ \|UAV\|_F = \|A\|_F, \quad \|UAV\|_2 = \|A\|_2.\]

Ovo posljednje svojstvo čini Frobeniusovu i spektralnu normu posebno pogodnim za teorijsku analizu. Nažalost, spektralnu normu je dosta teško računati u praksi.

Uvjetovanost problema#

Ranije smo definirali greške samo u slučaju skalarnih funkcija, pa proširimo prvo tu definiciju i na vektorske funkcije.

Definicija 1.18 (Apsolutna i relativna greška po normi)

Neka je \(V\) vektorski prostor, te \(x, \tilde{x} \in V\).

Apsolutna greška po normi aproksimacije \(\tilde{x} = x + \Delta x\) u odnosu na egzaktnu vrijednost \(x\) je \(\|\Delta x\| = \|\tilde{x} - x\|\).

Relativna greška po normi aproksimacije \(\tilde{x} = x + \Delta x\) u odnosu na egzaktnu vrijednost \(x\) je \(\frac{\|\Delta x\|}{\|x\|} = \frac{\|\tilde{x} - x\|}{\|x\|}\).

Uvedimo sada precizno pojam uvjetovanosti. Slično kao i kod grešaka, razlikujemo apsolutnu i relativnu uvjetovanost.

Definicija 1.19 (Apsolutna i relativna uvjetovanost)

Neka su \(V\) i \(W\) vektorski prostori, \(f : V \to W\) zadana funkcija te \(x \in V\) i \(y = f(x)\).

Apsolutna uvjetovanost funkcije \(f\) u točki \(x\) je

\[ \kappa_f^{\text{abs}}(x) := \lim_{\eps \to 0} \sup_{\|\Delta x\| \leq \eps} \frac{\|f(x+\Delta x) - f(x)\|}{\|\Delta x\|}. \]

Relativna uvjetovanost funkcije \(f\) u točki \(x\) je

\[ \kappa_f^{\text{rel}}(x) := \lim_{\eps \to 0} \sup_{\|\Delta x\|\leq \eps \|x\| } \frac{\delta_y}{\delta_x}, \]

gdje smo sa \(\delta_y\) označili relativnu grešku aproksimacije \(\tilde{y} = f(x+\Delta x)\) u odnosu na \(y = f(x)\), a sa \(\delta_x\) relativnu grešku aproksimacije \(\tilde{x} = x + \Delta x\) u odnosu na \(x\):

\[ \delta_y = \frac{\|f(x+\Delta x) - f(x)\|}{\|f(x)\|}, \quad \delta_x = \frac{\|\Delta x\|}{\|x\|}. \]

Objasnimo vezu gornje definicije i intuitivnog shvaćanja pojma uvjetovanosti. Promatrajmo sve \(\tilde{x} = x + \Delta x\) iz kruga radijusa \(\eps\) oko \(x\); oni zadovoljavaju \(\|\Delta x\| \leq \eps\). Slika \(\tilde{y} = f(\tilde{x})\) je udaljena za \(\|f(\tilde{x}) - f(x)\|\) od točke \(y = f(x)\). Dakle, apsolutna greška \(\|f(\tilde{x}) - f(x)\|\) u izlaznim podacima se u odnosu na apsolutnu grešku \(\|\Delta x\|\) u ulaznim podacima povećala s faktorom

\[ \frac{\|f(x+\Delta x) - f(x)\|}{\|\Delta x\|}. \]

U najgorem slučaju među svim točkama unutar kruga radijusa \(\eps\) oko \(x\) taj faktor iznosi

\[ \sup_{\|\Delta x\| \leq \eps} \frac{\|f(x+\Delta x) - f(x)\|}{\|\Delta x\|}. \]

Zanimaju nas samo malene perturbacije ulaznih podataka, pa zato u definiciji apsolutne uvjetovanosti gledamo \(\eps \to 0\). Slično je i za relativnu uvjetovanost.

Sasvim očekivano, uvjetovanost skalarnih funkcija povezana je s derivacijom. Prije iskaza teorema, potrebna nam je definicija tzv. Landauovog simbola \(\bigO(\cdot)\).

Definicija 1.20 (Laundauov simbol \(\bigO(\cdot)\))

Neka su \(g, h : \R^m \to \R^n\) funkcije, te \(x_0 \in \R^m\) takvi da postoje konstante \(\delta\) i \(C\) sa svojstvom

\[ (\forall x \in \R^m) \; \big( \; \|x - x_0\| \leq \delta \; \Rightarrow \|g(x)\| \leq C \|h(x)\| \; \big). \]

Tada kažemo da je funkcija \(g\) reda veličine \(h\) kad \(x \to x_0\) i pišemo \(g(x) = \bigO(h(x))\) ili \(g(x) \in \bigO(h(x))\) kada \(x \to x_0\).

Oznaka \(\bigO(\cdot)\) zove se Landauov simbol.

Tako je, na primjer:

\(\sin(x) \in \bigO(x)\) kad \(x \to 0\) jer \(|\sin(x)| \leq |x|\) za svaki \(x \in \R\).
\(\sin(x) = x + \bigO(x^3)\) kad \(x \to 0\) jer

\[|\sin(x) - x| = [\text{Taylor}] = \left| \frac{-x^3}{3!} + \frac{x^5}{5!} - \ldots \right| = |x^3| \cdot \underbrace{\left|\frac{-1}{6} + \frac{x^2}{5!} - \ldots\right|}_{<1/3 \text{ za dovoljno male } |x|} \leq \frac{1}{3}|x^3|. \]
\(x^2 + 3x = \bigO(x)\) kad \(x \to 0\) jer \(|x^2+3x| = |x| \cdot |x+3| \leq 4|x|\) za \(|x| \leq 1\).
\(x^2 - x - 6 = \bigO(x-3)\) kad \(x \to 3\) jer \(|x^2-x-6| = |x-3| \cdot |x+2| \leq 6|x-3|\) za \(|x-3| \leq 1\).

Teorem 1.21 (Uvjetovanost skalarnih funkcija)

Neka je dana funkcija \(f : \R \to \R\) klase \(C^2\). Tada je njezina apsolutna uvjetovanost dana sa

\[ \kappa_f^{\text{abs}}(x) = |f'(x)|, \]

a njena relativna uvjetovanost (za \(x \neq 0\))

\[ \kappa_f^{\text{rel}}(x) = \left|\frac{xf'(x)}{f(x)}\right|. \]

Dokaz.

Fiksirajmo \(x \in \R\) i pripadni \(y = f(x)\) te promatrajmo utjecaj \(\Delta x\) na \(\Delta y\). Primijenimo Taylorov teorem o polinomu prvog stupnja za \(f(x + \Delta x)\) oko \(x\): postoji \(\xi \in [0, 1]\) takav da je

\[ \Delta y = f(x + \Delta x) - f(x) = f'(x) \Delta x + \frac{f''(x + \xi \Delta x)}{2!} (\Delta x) ^2. \]

Funkcija \(f''\) je neprekidna na \([x, x+\Delta x]\), pa je i omeđena, što znači da možemo pisati \(f''(x + \xi \Delta x) = \bigO(1)\). Slijedi

\[ \Delta y = f'(x) \Delta x + \bigO( (\Delta x)^2 ), \]

to jest,

\[ \frac{\Delta y}{\Delta x} = f'(x) + \bigO( \Delta x ). \]

Stoga postoji konstanta \(C\) takva da je

\[ |f'(x)| - C |\Delta x| \leq \frac{|\Delta y|}{|\Delta x|} = |f'(x) + \bigO(\Delta x)| \leq |f'(x)| + C |\Delta x|. \]

Ovdje smo dvaput primijenili nejednakost trokuta. Sada uzmemo \(\sup_{|\Delta x| \leq \eps}\) i pustimo \(\eps \to 0\). Lijeva i desna strana konvergiraju ka \(|f'(x)|\) jer je \(\lim_{\eps \to 0} \sup_{|\Delta x| \leq \eps} C|\Delta x| = 0\), pa imamo

\[ |f'(x)| \leq \kappa_f^{\text{abs}}(x) \leq |f'(x)|, \]

iz čega trivijalno slijedi tvrdnja.

Za relativnu uvjetovanost ide slično:

\[\begin{split} \begin{align*} \frac{\Delta y}{y} &= \frac{f'(x) \Delta x + \bigO((\Delta x)^2)}{y} \\ &= \frac{x f'(x)}{y} \cdot \frac{\Delta x}{x} + \bigO\left(\frac{(\Delta x)^2}{y}\right) \\ &= \frac{x f'(x)}{y} \cdot \frac{\Delta x}{x} + \bigO\left(\frac{x^2}{y} \cdot \left( \frac{\Delta x}{x}\right)^2 \right). \end{align*} \end{split}\]

Kako je \(\frac{x^2}{y}\) konstanta (fiksirali smo \(x\) pa onda i \(y=f(x)\)), slijedi

\[\begin{split} \begin{align*} \frac{\Delta y}{y} &= \frac{x f'(x)}{y} \cdot \frac{\Delta x}{x} + \bigO\left( \left(\frac{\Delta x}{x}\right)^2 \right) \\ \end{align*} \end{split}\]

Dakle,

\[ \frac{\delta_y}{\delta_x} = \frac{|\Delta y| / |y|}{|\Delta x| / |x|} = \left| \frac{x f'(x)}{y} + \bigO\left(\frac{\Delta x}{x} \right) \right|, \]

pa posve analogno kao kod izvoda apsolutne uvjetovanosti slijedi

\[ \kappa_f^{\text{rel}}(x) = \left|\frac{xf'(x)}{f(x)}\right|. \]

Primjer 1.22

Promotrimo funkciju \(f(x) = \ln(x)\) za \(x \in \langle 0, \infty \rangle\). Kada je \(x \neq 1\), imamo

\[ \kappa_f^{\text{rel}}(x) = \left|\frac{xf'(x)}{f(x)}\right| = \left| \frac{1}{\ln(x)} \right|. \]

Relativna uvjetovanost je stoga velika kada je \(\ln(x) \approx 0\), tj. kada je \(x \approx 1\). To je i prirodno za očekivati: u maloj okolini od \(1\) je vrijednost \(\ln(x) \approx 0\) i samo malom promjenom \(x\) se može drastično promijeniti vrijednost logaritma.

Isprobajmo ovaj primjer i u Pythonu: uzmimo \(x=1.000001\) i \(\tilde{x} = 1.000002\).

import math;

x = 1.000001;
xtilde = 1.000002;
rel_greska_xtilde = abs(x-xtilde) / abs(x);

y = math.log(x);
ytilde = math.log(xtilde);
rel_greska_ytilde = abs(y-ytilde) / abs(y);

print( f'     x={x},           y=ln(x)={y:.16f}' );
print( f'xtilde={xtilde}, ytilde=ln(xtilde)={ytilde:.16f}\n' );

print( f'Relativna greška od xtilde je: {rel_greska_xtilde:.16f}' );
print( f'Relativna greška od ytilde je: {rel_greska_ytilde:.16f}\n' );

rel_uvjetovanost = 1.0 / abs( math.log(x) );
print( f'Relativna uvjetovanost ln(x) u točki x={x} je {rel_uvjetovanost}' );

print( f'Rel. uvjetovanost * rel. greška u x = {rel_uvjetovanost * rel_greska_xtilde}' );

     x=1.000001,           y=ln(x)=0.0000009999994999
xtilde=1.000002, ytilde=ln(xtilde)=0.0000019999980001

Relativna greška od xtilde je: 0.0000009999990001
Relativna greška od ytilde je: 0.9999990002235443

Relativna uvjetovanost ln(x) u točki x=1.000001 je 1000000.5000821833
Rel. uvjetovanost * rel. greška u x = 0.9999995002224611

Relativna greška u \(\tilde{x}\) je vrlo mala: \(\delta_x \approx 10^{-6}\). No \(y=\ln(x) \approx 10^{-6}\), a \(\tilde{y} = \ln(\tilde{x}) \approx 2 \cdot 10^{-6}\) pa je relativna greška u \(\tilde{y}\) jako velika: \(\delta_y \approx 1\). Razlog tako velikoj grešci je velika uvjetovanost funkcije \(\ln\) u točki \(x\) koja iznosi \(\kappa_{\ln}^{\text{rel}}(x) \approx 10^6\). Vidimo da vrijedi

\[ \text{rel. greška u } y \approx \text{ rel. uvjetovanost} \cdot \text{rel. greška u } x, \]

što je upravo ideja uvjetovanosti: greška u \(y\) se povećala s faktorom jednakim uvjetovanosti u odnosu na grešku u \(x\).

Uvjetovanost vektorskih funkcija pomoću uvjetovanosti skalarnih

Kada imamo funkciju \(f : \R^m \to \R^n\), osim promatranja uvjetovanosti po normi kao u Definiciji 1.19, mogli bismo promatrati uvjetovanost skalarnih funkcija koje pojedinim komponentama vektora \(x \in \R^m\) pridružuju komponente vektora \(y = f(x) \in \R^n\).

Na primjer, promotrimo operaciju oduzimanja \(f : \R^2 \to \R\), \(f(x_1, x_2) = x_1 - x_2\). Fiksirajmo neke vrijednosti od \(x_1\) i \(x_2\) i promotrimo kako promjena samo jedne od njih utječe na rezultat oduzimanja. Definiramo funkcije

\[\begin{split} \begin{align*} f_{x_1}(x) &= x - x_2 \; \leadsto \; \kappa_{f_{x_1}}^{\text{rel}}(x_1) = \frac{|x_1|}{|x_1-x_2|}, \\ f_{x_2}(x) &= x_1 - x \; \leadsto \; \kappa_{f_{x_2}}^{\text{rel}}(x_2) = \frac{|x_2|}{|x_1-x_2|}. \\ \end{align*} \end{split}\]

Očekivano, uvjetovanosti su velike kada je \(x_1 \approx x_2\), kako smo i vidjeli ranije.

Ovakav pristup je u principu jako teško provesti za složenije funkcije \(f\) i praktičnije je koristiti grublji pojam uvjetovanosti po normi iz Definicije 1.19.

I za vektorske funkcije \(f : \R^m \to \R^n\) možemo izvesti formule slične onima iz Teorema 1.21. Neka je \(x=(x_1, \ldots, x_m)\) i \(y=f(x)=(f_1(x), \ldots, f_n(x))\). Taylorov razvoj funkcije \(f_k(x + \Delta x)\) oko točke \(x\) glasi

\[\begin{split} f_k(x+\Delta x) &= f_k(x) + (\Delta x)^T \cdot \nabla f_k(x) + \bigO(\|\Delta x\|^2) \\ &= f_k(x) + \sum_{\ell=1}^m \frac{\partial f_k}{\partial x_\ell} \cdot \Delta x_\ell + \bigO(\|\Delta x\|^2), \end{split}\]

pa je

\[ \Delta y_k = f_k(x+\Delta x) - f_k(x) = \sum_{\ell=1}^m \frac{\partial f_k}{\partial x_\ell} \cdot \Delta x_\ell + \bigO(\|\Delta x\|^2). \]

Stoga vektor \(\Delta y\) možemo zapisati pomoću Jacobijeve matrice:

\[\begin{split} \Delta y = \mb{c} \Delta y_1 \\ \Delta y_2 \\ \vdots \\ \Delta y_n \me = D_f(x) \Delta x + \bigO(\|\Delta x\|^2), \quad D_f(x) = \mb{ccc} \frac{\partial f_1}{\partial x_1} & \ldots & \frac{\partial f_1}{\partial x_m} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1} & \ldots & \frac{\partial f_n}{\partial x_m} \me. \end{split}\]

Uzimanjem (operatorske) norme, slijedi

pa možemo uzeti da je

(1.2)#\[ \kappa_f^{\text{abs}}(x) = \|D_f(x)\| \]

apsolutna uvjetovanost po normi. (Uočite da smo zapravo dokazali samo \(\leq\).)

Slično, za relativnu uvjetovanost imamo

\[ \frac{\|\Delta y\|}{\|y\|} \leq \frac{\|D_f(x)\| \cdot \|\Delta x\| + \bigO(\|\Delta x\|^2)}{\|f(x)\|} = \frac{\|x\| \cdot \|D_f(x)\|}{\|f(x)\|} \cdot \frac{\|\Delta x\|}{\|x\|} + \bigO \left( \left( \frac{\|\Delta x\|}{\|x\|} \right)^2 \right). \]

Sada kao i u skalarnom slučaju slijedi (ponovno smo dokazali samo \(\leq\)):

(1.3)#\[ \kappa_f^{\text{rel}}(x) = \frac{\|x\| \cdot \|D_f(x)\|}{\|f(x)\|}. \]

U slučaju \(m=n=1\), izvedeni izrazi (1.2) i (1.3) se podudaraju s onima iz Teorema 1.21.

Primjer analize uvjetovanosti: Millerov algoritam#

Sada ćemo vidjeti jedan praktični primjer u kojem uvjetovanost onog što računamo ima ključnu ulogu za (ne)uspjeh. Cilj je, za zadani \(n\), izračunati vrijednosti integrala

\[ y_n := \int_0^1 \frac{t^n}{t+5} dt. \]

Lako se vidi da vrijedi rekurzivna formula

\[\begin{split} \left\{ \; \begin{array}{l} y_k = -5 y_{k-1} + \frac{1}{k}, \quad k=1, 2, \ldots, n \\ y_0 = \ln(6/5). \end{array} \right. \end{split}\]

Implementirajmo ovo u Pythonu i usporedimo s egzaktnim vrijednostima integrala (njih nam daje funkcija quad iz biblioteke scipy.integrate).

 n           yn               egzaktni integral     rel. greška
---------------------------------------------------------------
2.8468352225249460e-02  2.8468352225126427e-02  4.3e-12
1.5367550063685786e-02  1.5367550448186112e-02  2.5e-08
1.0521935097803692e-02  1.0520733534289037e-02  1.1e-04
4.2426370449215600e-03  7.9975230282321660e-03  4.7e-01
1.1740469003112501e+01  6.4503052668652174e-03  1.8e+03
-3.6668803026134643e+04  5.4046329651406813e-03  6.8e+06
1.1459002635079944e+08  4.6506691337970529e-03  2.5e+10
-3.5809383233171075e+11  4.0812982539260995e-03  8.8e+13

Vidimo da se vrijednosti \(y_n\) drastično razlikuju od egzaktnih integrala već za \(n=20\), te da za imalo veće \(n\) izgube svaku točnost.

Da analiziramo što se dogodilo, promotrimo funkciju koja početnom članu niza \(y_0\) pridružuje \(y_n\), tj. \(f : \R \to \R\), \(f(y_0) = y_n\). Indukcijom se lako pokaže da vrijedi

\[ f(y_0) = y_n = (-5)^n y_0 + \underbrace{\sum_{k=1}^n \frac{(-5)^{n-k}}{k}}_{\text{ne ovisi o } y_0!} \]

Relativna uvjetovanost funkcije \(f\) je

\[ \kappa_f^{\text{rel}}(y_0) = \left| \frac{y_0 f'(y_0)}{f(y_0)} \right| = \left| \frac{y_0 (-5)^n}{y_n} \right|. \]

Kako očito vrijedi \(y_0 > y_1 > \ldots > y_n\), slijedi

\[ \kappa_f^{\text{rel}}(y_0) > \left| \frac{y_0 (-5)^n}{y_0} \right| = 5^n. \]

Funkcija \(f\) je vrlo loše uvjetovana za imalo veći \(n\) i stoga je ekstremno osjetljiva na male perturbacije ulaznog podatka. Na primjer, uvjetovanost za \(n=25\) je veća od \(10^{17}\). Kako početni član \(y_0 = \ln(6/5)\) na računalu spremimo u varijablu tipa binary64 s relativnom greškom \(\eps \approx 1.11 \cdot 10^{-16}\), relativna greška u izračunatoj vrijednosti od \(f(y_0)\) će biti

\[ \approx \text{ uvjetovanost od f } \cdot \text{ greška u ulaznim podacima } > 10^{17} \cdot 10^{-16} = 10^1. \]

To znači da niti jedna znamenka od \(y_{25}\) neće biti točno izračunata – i upravo to se dogodilo! U svakom koraku petlje se greška povećala s faktorom 5.

Kako popraviti izračun integrala? Odgovor je vrlo zanimljiv: napišimo rekurziju unatrag, tj. izrazimo \(y_{k-1}\) pomoću \(y_k\):

\[\begin{split} \left\{ \; \begin{array}{l} y_{k-1} = \frac{1}{5} \left(\frac{1}{k} - y_{k} \right), \quad k=N, N-1, \ldots, n+1 \\ y_N = ???. \end{array} \right. \end{split}\]

Kad bismo znali vrijednost \(y_N\) za neki \(N > n\), onda bismo gornjom rekurzijom mogli izračunati \(y_n\). Prije odgovora kako možemo znati \(y_N\), promotrimo uvjetovanost funkcije \(g : \R \to \R\) koja vrijednosti \(y_N\) pridružuje \(y_n\), tj. \(g(y_N) = y_n\). Kao i kod funkcije \(f\), imamo

\[ g(y_N) = y_n = \left( \frac{-1}{5} \right)^{N-n} y_N + \underbrace{\sum_{k=n+1}^N \frac{(-1)^{k-n-1}}{5^{k-n}k}}_{\text{ne ovisi o } y_N!} \]

Istom analizom kao prije, dobivamo da za relativnu uvjetovanost funkcije \(g\) vrijedi

\[ \kappa_g^{\text{rel}}(y_N) < \left( \frac{1}{5} \right)^{N-n} < 10^{-19} \; \text{ za } \; N=n+28. \]

Sada imamo prigušenje greške s faktorom \(\frac{1}{5}\) u svakom koraku! To znači da možemo uzeti posve pogrešnu vrijednost \(y_N\) i vrijednost \(y_n = g(y_N)\) će biti vrlo točna?! Ako stavimo \(N=n+28\), faktor prigušenja greške će biti veći od \(10^{19}\), pa će konačni rezultat biti točan na 16 znamenki čak i ako je polazna vrijednost \(y_N\) imala relativnu grešku \(1000\).

Isprobajmo ovaj algoritam u Pythonu. Uvijek ćemo početi sa \(y_N=0\) čime je napravljena relativna greška \(1\), kolika god bila stvarna vrijednost od \(y_N\).

 n           yn               egzaktni integral     rel. greška
---------------------------------------------------------------
2.8468352225126420e-02  2.8468352225126427e-02  2.4e-16
1.5367550448186114e-02  1.5367550448186112e-02  1.1e-16
1.0520733534289034e-02  1.0520733534289037e-02  3.3e-16
7.9975230282321643e-03  7.9975230282321660e-03  2.2e-16
6.4503052668652156e-03  6.4503052668652174e-03  2.7e-16
5.4046329651406795e-03  5.4046329651406813e-03  3.2e-16
4.6506691337970503e-03  4.6506691337970529e-03  5.6e-16
4.0812982539260969e-03  4.0812982539260995e-03  6.4e-16

Svi integrali su izračunati točno na 16 decimala! Ovaj trik s okretanjem rekurzije se naziva Millerov algoritam.

Uvjetovanost računanja nultočki polinoma#

Nultočke polinoma mogu biti jako osjetljive na male perturbacije koeficijenata. Klasični primjer koji to ilustrira je tzv. Wilkinsonov polinom

\[ p_{20}(x) = (x-1)(x-2) \ldots (x-20). \]

Jasno, ovaj polinom ima nultočke 1, 2, \(\ldots\), 20. Zapišimo polinom u kanonskoj bazi:

\[ p_{20}(x) = x^{20} + c_{19} x^{19} + \ldots + c_1 x + c_0. \]

Wilkinsonov polinom:

x**20 - 210*x**19 + 20615*x**18 - 1256850*x**17 + 53327946*x**16 - 1672280820*x**15 + 40171771630*x**14 - 756111184500*x**13 + 11310276995381*x**12 - 135585182899530*x**11 + 1307535010540395*x**10 - 10142299865511450*x**9 + 63030812099294896*x**8 - 311333643161390640*x**7 + 1206647803780373360*x**6 - 3599979517947607200*x**5 + 8037811822645051776*x**4 - 12870931245150988800*x**3 + 13803759753640704000*x**2 - 8752948036761600000*x + 2432902008176640000

Koeficijenti polinoma: 
c_0 = 2432902008176640000
c_1 = -8752948036761600000
c_2 = 13803759753640704000
c_3 = -12870931245150988800
c_4 = 8037811822645051776
c_5 = -3599979517947607200
c_6 = 1206647803780373360
c_7 = -311333643161390640
c_8 = 63030812099294896
c_9 = -10142299865511450
c_10 = 1307535010540395
c_11 = -135585182899530
c_12 = 11310276995381
c_13 = -756111184500
c_14 = 40171771630
c_15 = -1672280820
c_16 = 53327946
c_17 = -1256850
c_18 = 20615
c_19 = -210

Vidimo da su neki koeficijenti ekstremno veliki. Najveći čak ne stanu u punoj točnosti u tip binary64 (mi smo u Pythonu koristili simbolički račun koji daje egzaktne vrijednosti).

Promotrimo perturbirani polinom

\[ \tilde{p}_{20}(x) = p_{20}(x) - 2^{-23} x^{19}. \]

Promijenili smo samo koeficijent \(c_{19}\) i unijeli u njega relativnu grešku koja je reda veličine samo \(2^{-30}\), tj. manja od \(10^{-9}\). Svi ostali koeficijenti polinoma \(\tilde{p}_{20}\) su isti kao kod \(p_{20}\). Koliko su se promijenile nultočke polinoma?

Nultočke perturbiranog polinoma ptilde_20: 
(1+0j)
(2+0j)
(2.999999999999805+0j)
(4.000000000261023+0j)
(4.999999927551538+0j)
(6.000006943952296+0j)
(6.999697233936014+0j)
(8.007267603450376+0j)
(8.917250248517071+0j)
(20.846908101482256+0j)
(10.095266145129964+0.6435009038636036j)
(10.095266145129964-0.6435009038636036j)
(11.793633881079433-1.6523297281609324j)
(11.793633881079433+1.6523297281609324j)
(19.50243940049368+1.9403303466644795j)
(19.50243940049368-1.9403303466644795j)
(13.992358137235671+2.518830069630272j)
(13.992358137235671-2.518830069630272j)
(16.730737466090705-2.8126248942700394j)
(16.730737466090705+2.8126248942700394j)

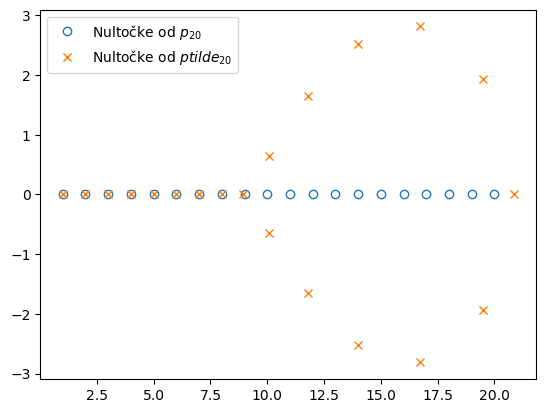
_images/b5b7f9c8f06ed79f6901dc67bb7d295282f4d598e5e18963dbe296b2e91a1dfc.png

Vidimo da su se nultočke od \(\tilde{p}_{20}\) u odnosu na nultočke od \(p_{20}\) promijenile puno više od promjene koeficijenta koja je iznosila samo \(2^{-23}\). Uvjetovanost funkcije koja prima koeficijente polinoma, a vraća njegove nultočke je ekstremno velika za koeficijente polinoma \(p_{20}\).

Ovakva potencijalno vrlo velika osjetljivost nultočki polinoma na male perturbacije njegovih koeficijenata ima za posljedicu da se svojstvene vrijednosti matrice \(A\) u praksi nikad ne računaju kao nultočke karakterističnog polinoma. Umjesto toga, postoje specijalizirane metode upravo za rješavanje svojstvenog problema. Neke od njih se rade na kolegiju Numerička analiza 1 s diplomskog studija.

Primjer: Uvjetovanost računanja sume \(n\) brojeva#

Za kraj ove cjeline, napravimo analizu računanja sume \(s = x_1 + x_2 + \ldots + x_n\) u aritmetici konačne preciznosti pomoću sljedećeg algoritma:

Algoritam 1.23

\(s = x_1\);
for \(i = 2, 3, \ldots, n\)
\(s = s + x_i\);

Ako su brojevi \(x_1, \ldots, x_n\) već spremljeni u računalu, odredimo rezultat koji uključuje greške zaokruživanja. Označimo sa \(s_i\) vrijednost varijable \(s\) nakon izvršavanja tijela petlje za index \(i\):

\[\begin{split} \begin{align*} s_2 &= \fl( x_1 + x_2 ) = x_1 (1 + \eps_1) + x_2 (1+\eps_1) \\ s_3 &= \fl( s_2 + x_3 ) = s_2 (1 + \eps_2) + x_3 (1+\eps_2) \\ &\quad\quad = x_1 (1 + \eps_1)(1 + \eps_2) + x_2 (1+\eps_1)(1 + \eps_2) + x_3 (1 + \eps_2) \\ & \vdots \\ \end{align*} \end{split}\]

i na kraju dobivamo

\[\begin{split} \begin{align*} \tilde{s} = s_n &= \fl( s_{n-1} + x_3 ) \\ &= s_{n-1} (1 + \eps_{n-1}) + x_n (1+\eps_{n-1}) \\ &= \underbrace{x_1 (1 + \eps_1)(1 + \eps_2) \ldots (1+\eps_{n-1})}_{\tilde{x}_1 = x_1 (1 + \eta_1)} + \underbrace{x_2 (1+\eps_1)(1 + \eps_2)\ldots (1+\eps_{n-1})}_{\tilde{x}_2 = x_2 (1 + \eta_2)} + \ldots \\ &\quad\quad + \underbrace{x_{n-1} (1 + \eps_{n-2})(1 + \eps_{n-1})}_{\tilde{x}_{n-1} = x_{n-1} (1 + \eta_{n-1})} + \underbrace{x_n(1+\eps_{n-1})}_{\tilde{x}_n = x_n (1 + \eta_n)}, \end{align*} \end{split}\]

gdje su \(|\eps_1|, \ldots, |\eps_{n-1}| \leq u\). Vidimo da je suma \(\tilde{s}\) dobivena na računalu jednaka egzaktnoj sumi malo perturbiranih pribrojnika \(\tilde{x}_i\). Očekujemo da vrijedi

\[ |\eta_1| \approx |\eta_2| \gtrsim |\eta_3| \gtrsim \ldots \gtrsim |\eta_{n-1}|, \]

te \(|\eta_i| \lesssim (n-i+1) \cdot u\). Relativna greška izračunatog \(\tilde{s}\) u odnosu na egazktni je

\[ \frac{|\tilde{s} - s|}{|s|} = \underbrace{\frac{|\eta_1 x_1 + \ldots + \eta_n x_n|}{|x_1 + \ldots + x_n|}}_E \leq \frac{|x_1| + \ldots + |x_n|}{|x_1 + \ldots + x_n|} \cdot \max_i |\eta_i| \leq \underbrace{\frac{|x_1| + \ldots + |x_n|}{|x_1 + \ldots + x_n|} \cdot n}_{\kappa_s} \cdot u. \]

Vidimo da broj \(\kappa_s\) prestavlja uvjetovanost gornjeg algoritma u aritmetici računala: on predstavlja faktor s kojim se rel. greška u ulaznim podacima (greška u prikazu \(x_i\) u računalu) množi da dobijemo rel. grešku u rezultatu. Uvjetovanost može biti velika ako je egzaktni rezultat blizu nule, kao i ranije kod zbrajanja dva broja.

Ako su svi brojevi \(x_i\) istog predznaka:

Uvjetovanost \(\kappa_s\) je samo \(n\).
Očekujemo da je izraz \(E\) najmanji kada je \(x_1 \leq x_2 \leq \ldots \leq x_n\).
Drugim riječima, očekujemo da je greška u zbrajanju \(n\) brojeva najmanja kada brojeve zbrajamo u uzlazno sortiranom poretku.