6.3. Uvod u optimizaciju#
Sad ćemo promatrati probleme optimizacije; dati ćemo samo pregled nekih osnovnih ideja, bez ulaženja u detalje. Kod problema optimizacije, zadana je funkcija \(f : \R^n \to \R\), koju zovemo funkcija cilja. Možemo imati jedan od dva sljedeća zadatka:
Potrebno je odrediti minimum funkcije \(f\) na cijelom \(\R^n\). U tom slučaju govorimo o problemu bezuvjetne optimizacije.
Potrebno je odrediti minimum funkcije \(f\) na nekom podskupu \(\Omega \subseteq \R^n\). Tipično je \(\Omega\) zadan ili kao skup svih \(\theta \in \R^n\) koji su rješenja neke jednadžbe \(h(\theta) = 0\) ili kao skup svih \(\theta \in \R^n\) koji su rješenja neke nejednadžbe \(h(\theta) \leq 0\), ili pak kao kombinacija takvih uvjeta. U tom slučaju govorimo o problemu uvjetne optimizacije.
Argumente \(\theta\) funkcije \(f\) obično zovemo parametrima optimizacije. U ovom kolegiju ćemo se baviti samo problemima bezuvjetne optimizacije.
Neka je dana funkcija \(f : \R^n \to \R\). Ako je \(\theta_\ast \in \R^n\) takva da vrijedi
kažemo da se u točki \(\theta_\ast\) postiže globalni minimum funkcije \(f\).
Ako postoji \(\eps > 0\) takav da vrijedi
onda kažemo da se u točki \(\theta_\ast\) postiže lokalni minimum funkcije \(f\).
U ovoj cjelini ćemo pretpostavljati da je \(f \in C^1(\R^n)\). Općenito želimo pronaći globalni minimum funkcije \(f\), no metode koje koristimo će tipično konvergirati točkama lokalnih minimuma. Na kolegijima matematičke analize smo naučili da se lokalni minimumi takvih funkcija nužno nalaze u stacionarnim točkama, odnosno, za svaki lokalni minimum \(\theta_\ast\) mora vrijediti
Kako je (6.8) jedan sustav nelinearnih jednadžbi, za njegovo rješavanje ćemo moći primijeniti neku od numeričkih metoda koje smo razvili u prethodnoj cjelini, no pokazat ćemo i neke druge ideje.
Metode spusta#
Neka je zadana funkcija \(f : \R^n \to \R\) čiji minimum želimo odrediti. Za zadanu početnu vrijednost parametara \(\theta^{(0)} \in \R^n\), promotrimo sljedeći niz:
Ovdje je \(d^{(k)} \in \R^n\) pogodno odabrani smjer, a \(\eta_k > 0\) realni broj koji zovemo veličina koraka. U kontekstu strojnog učenja, \(\eta_k\) još zovemo faktor brzine učenja (eng. learning rate). Kako nas zanima minimizacija funkcije \(f\), prirodno pitanje koje se postavlja je sljedeće:
Kako odabrati \(d^{(k)}\) tako da on bude smjer silaska? Kažemo da je \(d^{(k)}\) smjer silaska ako za svaki dovoljno mali \(\eta_k > 0\) vrijedi
\[ f(\theta^{(k)} + \eta_k \cdot d^{(k)}) < f(\theta^{(k)}), \]to jest, u idućoj iteraciji \(\theta^{(k+1)}\) se postiže manja vrijednost funkcije \(f\) nego u iteraciji \(\theta^{(k)}\).
Vektor \(d^{(k)}\) je smjer silaska ako i samo ako vrijedi
Promotrimo funkciju \(g : \R \to \R\) definiranu sa \(g(t) = f(\theta^{(k)} + t d^{(k)})\). Uočimo da je \(g(0) = f(\theta^{(k)})\). Iz uvjeta \(f(\theta^{(k)} + t \cdot d^{(k)}) < f(\theta^{(k)})\) slijedi \(g(t) < g(0)\) za \(t > 0\), tj. funkcija \(g\) je padajuća u točki \(0\). Kako je \(g \in C^1(\R)\), to je ekvivalentno sa \(g'(0) < 0\). Vrijedi
Uvrštavanjem \(t=0\) slijedi tvrdnja propozicije.
Različiti izbori \(d^{(k)}\) odgovaraju različitim metodama optimizacije. Ovdje ćemo diskutirati samo dvije takve metode.
Newtonova metoda minimizacije. Kada rješavamo sustav nelinearnih jednadžbi \(\nabla f(\theta) = 0\), Newtonova metoda generira niz aproksimacija
\[ \theta^{(k+1)} = \theta^{(k)} - J_{\nabla f}(\theta^{(k)})^{-1} \cdot \nabla f(\theta^{(k)}) = \theta^{(k)} - H_{f}(\theta^{(k)})^{-1} \cdot \nabla f(\theta^{(k)}). \]Dakle, ovdje je
\[ d^{(k)} = -H_{f}(\theta^{(k)})^{-1} \cdot \nabla f(\theta^{(k)}), \]pri čemu je \(H_{f}(\theta^{(k)})\) Hessijan funkcije \(f\) u točki \(\theta^{(k)}\). Ako je Hessijan pozitivno definitan u točki \(\theta^{(k)}\) (a to očekujemo ako je \(\theta^{(k)}\) blizu minimuma \(\theta_\ast\)!), onda će \(d^{(k)}\) biti smjer silaska, jer je tada
\[ \langle -H_{f}(\theta^{(k)})^{-1} \cdot \nabla f(\theta^{(k)}), \nabla f(\theta^{(k)}) \rangle < 0 \]za \(\nabla f(\theta^{(k)}) \neq 0\).
Metoda gradijentnog spusta ili metoda najbržeg spusta (eng. gradient descent). Stavimo jednostavno
\[ d^{(k)} = -\nabla f(\theta^{(k)}), \]tj.
\[ \theta^{(k+1)} = \theta^{(k)} - \eta_k \nabla f(\theta^{(k)}). \]Očito je \(\langle d^{(k)}, \nabla f(\theta^{(k)}) \rangle = -\|\nabla f(\theta^{(k)})\|^2 \leq 0\), pa je \(d^{(k)}\) smjer silaska ako \(\nabla f(\theta^{(k)}) \neq 0\).
Za Newtonovu minimizacijsku metodu možemo pokazati slične rezultate konvergencije kao i kod sustava nelinearnih jednadžbi: ta metoda lokalno kvadratično konvergira prema točki minimuma \(\theta_\ast\). Međutim, postoje sljedeće poteškoće:
Nije realno očekivati da je \(H_f(\theta^{(k)})\) pozitivno definitna osim kada je \(\theta^{(k)}\) u sasvim maloj okolini točke minimuma \(\theta_\ast\). Stoga već početna iteracija \(\theta^{(0)}\) mora biti dosta dobra aproksimacija od \(\theta_\ast\) kako bi smjerovi \(d^{(k)}\) bili smjerovi silaska.
Računanje matrice \(H_f(\theta^{(k)})\) i rješavanje sustava s tom matricom u svakoj iteraciji je tipično vrlo zahtjevno, pogotovo kad je broj varijabli \(n\) po kojima radimo optimizaciju velik.
Stoga se u praksi često koriste i kvazi-Newtonove metode koje umjesto egzaktnog Hessijana koriste neku njegovu numeričku aproksimaciju, poput metode BFGS. Time se nastoji riješiti druga gore navedena poteškoća. Prva poteškoća je problematična i kod drugih metoda optimizacije. Općenito, čim funkcija cilja nije konveksna (tj. Hessijan joj nije pozitivno definitan u svakoj točki domene), teško je pokazati bilo kakav rezultat o konvergenciji.
Ni pitanje izbora parametra \(\eta_k\) nije trivijalno.
Možemo uvijek uzeti dovoljno maleni, konstantni korak \(\eta_k = \eta\). Ako je korak prevelik, metoda neće konvergirati; ako je premalen, konvergirat će sporo.
Druga mogućnost je da pokušamo naći optimalni \(\eta_k\), tj. onaj koji je rješenje sljedećeg problema u jednoj dimenziji:
\[ \min_{\eta > 0} f(\theta^{(k)} + \eta \cdot d^{(k)}). \]Ovaj pristup odabiru \(\eta_k\) se iz očitih razloga zove pretraživanje po pravcu (eng. line search). Ovisno o složenosti funkcije \(f\), nalaženje ovakvog \(\eta_k\) može biti netrivijalno jer je potrebno ponovno rješavati optimizacijski problem (iako sada samo u jednoj varijabli).
Možemo koristiti razne heurističke pristupe za izbor \(\eta_k\). Na primjer, Armijov korak definira \(\eta_k\) ovako: neka su \(\alpha, \beta \in \langle 0, 1 \rangle\) neki parametri (tipično, \(\alpha = 10^{-2}\), \(\beta = \frac{1}{2}\)). Na početku odaberemo neki \(\eta_k > 0\). Sve dok uvjet
\[ f(\theta^{(k)}) - f(\theta^{(k)} + \eta_k \cdot d^{(k)}) \geq -\alpha \cdot \eta_k \cdot \nabla \langle f(\theta^{(k)}), \, d^{(k)} \rangle \]nije zadovoljen, zamijenimo \(\eta_k\) sa \(\beta \cdot \eta_k\). Nakon dovoljno mnogo ovakvih koraka, gornji uvjet će biti zadovoljen.
Mi ćemo se u nastavku više posvetiti metodi gradijentnog spusta:
Za ilustraciju, pokažimo samo najjednostavniji rezultat o konvergenciji.
Neka je \(\theta_\ast\) stacionarna točka funkcije \(f \in C^1(\R)\), tj. \(\nabla f(\theta_\ast) = 0\). Pretpostavimo da je preslikavanje
kontrakcija s faktorom \(q\). Tada gradijentni spust s konstantnim korakom \(\eta\) konvergira ka \(\theta_\ast\) za svaki početni izbor parametara \(\theta^{(0)}\).
Tvrdnja lako slijedi jer zbog
induktivnim argumentom imamo \(\|\theta^{(k)} - \theta_\ast\| \leq q^k \|\theta^{(0)} - \theta_\ast\|\), pa niz \((\theta^{(k)})_k\) linearno konvergira ka \(\theta_\ast\).
Napomena
Ako je \(f \in C^2(\R^2)\), onda zahtjev da je funkcija \(\varphi\) iz prethodne propozicije kontrakcija povlači da je funkcija \(f\) konveksna.
Zaista, za proizvoljni vektor \(h \neq 0\) i \(t \in \R\) vrijedi
a s druge strane je
gdje je \(H_f\) Hessijan. Dakle, za svaki \(h \neq 0\) je \(\|(I - \eta H_f(\theta)) h\| \leq q \|h\|\), pa je \(\|I - \eta H_f(\theta)\|_2 \leq q\). Neka su \(\lam_1, \ldots, \lam_n \in \R\) svojstvene vrijednosti simetrične matrice \(H_f(\theta)\). Tada su svojstvene vrijednosti od \(I - \eta H_f(\theta)\) jednake \(1 - \eta \lam_i\), pa je
iz čega slijedi \(\frac{1 - q}{\eta} \leq \lam_i \leq \frac{1 + q}{\eta}\). Stoga je matrica \(H_f(\theta)\) pozitivno definitna zbog \(0 < q < 1\) i \(\eta > 0\).
Koristeći Armijo korak, može se pokazati da niz iteracija gradijentnog spusta ima gomilišta u stacionarnim točkama i bez zahtjeva na konveksnost.
Neka je \(f : \R^n \to \R\) klase \(C^1\). Tada gradijentna metoda uz Armijov izbor koraka dolazi do stacionarne točke u konačno mnogo koraka ili formira niz \(\theta^{(k)}\) čije je svako gomilište stacionarna točka funkcije \(f\).
Dokaz možete pronaći u materijalima za izborni diplomski kolegij Uvod u optimizaciju.
Stohastički gradijentni spust#
Podsjetimo se problema najmanjih kvadrata; ovdje ćemo malo prilagoditi notaciju. Imali smo mjerenja \((x_i, y_i)\), \(i=1, \ldots, N\) i cilj je bio pronaći minimum funkcije
gdje su nam funkcije \(\varphi_j\) bile unaprijed zadane. Vidimo da funkcija cilja ovdje ima oblik
pri čemu funkcija \(g\) ovisi i o mjerenju. Ako ovih mjerenja ima jako puno, tj. \(N\) je velik, onda je računanje gradijenta funkcije \(f\) računski vrlo zahtjevno. Stoga u praksi, umjesto metode gradijentnog spusta koja u svakom koraku računa \(\nabla f(\theta)\), koristimo jednu od sljedećih varijacija:
Stohastički gradijentni spust.
Slučajno odaberemo neki index \(i\).
U \(k\)-tom koraku koristimo samo gradijent funkcije \(g\) izračunat za mjerenje \((x_i, y_i)\).
\[ \theta^{(k+1)} = \theta^{(k)} - \eta_k \cdot \nabla g(\theta^{(k)}; x_i, y_i). \]Postupak ponavljamo s novim, slučajno odabranim indexom.
Stohastički gradijentni spust s grupama (eng. batched stochastic gradient descent).
Slično kao i gore, skup \(G\) koji se sastoji od \(B\) slučajno odabranih indexa mjerenja.
U \(k\)-tom koraku koristimo samo gradijente za podatke s indexima iz skupa (grupe) \(G\):
\[ \theta^{(k+1)} = \theta^{(k)} - \frac{\eta_k}{B} \cdot \sum_{i \in G} \nabla g(\theta^{(k)}; x_i, y_i). \]Postupak ponavljamo s novom, slučajno odabranim grupom indexa.
Ideja stohastičkog gradijentnog spusta
Osnovna ideja stohastičkog gradijentnog spusta dolazi iz statistike. Pojmove koje koristimo u nastavku (distribucija, slučajna varijabla, očekivanje) ćete učiti na kolegiju Statistika na trećoj godini. Ovdje ih koristimo na intuitivnoj razini.
Promotrimo prvo stohastički gradijentni spust gdje slučajno (koristeći uniformnu distribuciju \(U\)) odabiremo jedan index \(i\) iz skupa \(\{1, 2, \ldots, N\}\). Koje je očekivanje slučajne varijable \(\nabla g(\theta^{(k)}; x_i, y_i)\)?
Kako je očekivanje upravo jednako željenoj vrijednosti \(\nabla f(\theta^{(k)})\), nakon puno iteracija stohastičkog gradijentnog spusta, u prosjeku smo odabirali ispravni smjer spusta. Posve analogno, nije teško pokazati da isto vrijedi i u slučaju stohastičkog gradijentnog spusta s grupama.
Stohastički gradijentni spust radi vrlo grubu aproksimaciju za \(\nabla f(\theta)\), pa očekujemo da će u praksi broj iteracija biti veći nego kod standardnog gradijentnog spusta; s druge strane, svaka iteracija je računski puno jeftinija. Korištenjem grupa radimo kompromis između kvalitete aproksimacije za \(\nabla f(\theta)\) i računske zahtjevnosti. Uvjerimo se u to jednim jednostavnim primjerom problema najmanjih kvadrata.
Primjer. Generirajmo slučajno \(N=100\) točaka oblika \(y_i = 3 \cdot x_i + 4 + 0.5\cdot\omega_i\), gdje je \(\omega_i\) slučajan broj iz normalne distribucije, a \(x_i\) je slučajan broj iz \([-5, 5]\) iz uniformne distribucije.
import numpy as np;
import matplotlib.pyplot as plt;
N = 100;
# Generiramo N slučajnih točaka xi uniformno u [-5, 5].
x = -5 + 10 * np.random.rand( N );
# Generiramo y = 3*x+4, dodamo slučajni Gaussov šum.
y = 3*x + 4 + 0.5*np.random.randn( N );
# Nacrtamo točke.
plt.scatter( x, y );
plt.xlabel( '$x_i$' );
plt.ylabel( '$y_i$' );
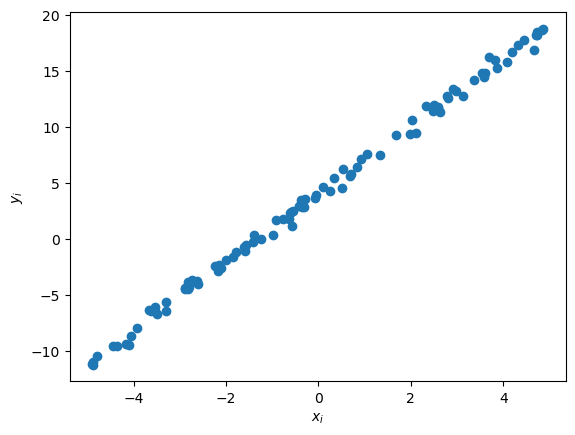
Cilj je samo na temelju podataka \((x_i, y_i)\), \(i=1, \ldots, N\), rekonstruirati optimalne koeficijente \(\theta_1^\ast = 3\) i \(\theta_2^\ast = 4\) u aproksimaciji \(y \approx \theta_1 x + \theta_2\). Promotrimo stoga funkciju cilja
gdje je \(g(\theta; x, y) = (y - \theta_1 x - \theta_2)^2\). Ranije smo pokazali kako njezin minimum egzaktno izračunati rješavanjem normalnih jednadžbi te korištenjem QR ili SVD dekompozicije. Sada ćemo minimum pronaći iterativno, korištenjem metoda gradijentnog spusta, stohastičkog gradijentnog spusta i stohastičkog gradijentnog spusta s grupama veličine \(10\). Ovaj pristup će biti općenitiji, tj. moći ćemo rješavati i druge probleme osim problema najmanjih kvadrata.
Prvo definiramo funkciju \(g\) i njezin gradijent \(\nabla g(\theta_1, \theta_2) = \mb{c} -2(y - \theta_1 x - \theta_2)x \\ -2(y - \theta_1 x - \theta_2) \me\), te funkciju cilja \(f(\theta) = \frac{1}{N} \sum_{i=1}^N g(\theta; x_i, y_i)\).
import numpy as np;
def g(theta, x, y):
# theta = [theta1, theta2]; x, y su skalari (jedno mjerenje).
return (y - theta[0]*x - theta[1])**2;
def grad_g(theta, x, y):
# theta = [theta1, theta2]; x, y su skalari (jedno mjerenje).
return np.array( [
-2*(y - theta[0]*x - theta[1])*x,
-2*(y - theta[0]*x - theta[1])
] );
def f(theta, x, y):
# Funkcija cilja.
# theta = [theta1, theta2]; x, y su polja koja sadrže sva mjerenja.
# Broj mjerenja.
N = x.shape[0];
ftheta = 0;
for i in range( 0, N ):
ftheta = ftheta + g(theta, x[i], y[i]);
return ftheta / N;
Zatim implementiramo sve tri metode. Prvo standardni gradijentni spust, uz fiksnu veličinu koraka \(\eta\). Eksperimentiramo s vrijednostima \(\eta = 0.1\), \(\eta = 0.03\) i \(\eta = 0.01\).
def grad_spust( x, y, g, grad_g, theta0, eta, n_epoch ):
# Ulaz:
# x = polje točaka u kojima su vršena mjerenja, duljine N
# y = polje izmjerenih vrijednosti za svaku točku iz x
# g = funkcije koja čini jedan pribrojnik funkcije cilja koju treba minimizirati.
# grad_g = funkcija koja računa gradijent od g
# theta0 = početne vrijednosti parametara
# eta = (konstantni) korak u metodi gradijentnog spusta
# n_epoch = broj iteracija koje treba provesti.
# Izlaz:
# theta = vrijednost parametara nakon n_epoch iteracija gradijentnog spusta
# hist = polje vrijednosti funkcije cilja nakon svakog koraka gradijentnog spusta. Samo za crtanje grafa.
# Broj mjerenja.
N = x.shape[0];
# Početna vrijednost parametara. Prazno polje hist.
theta = theta0; hist = [];
# Iteracije.
for epoch in range( 0, n_epoch ):
# Izračunaj gradijent funkcije f = 1/N * suma( g(theta, x_i, y_i) ).
grad = np.array( [0, 0] );
for i in range( 0, N ):
grad = grad + grad_g( theta, x[i], y[i] );
# Iduća iteracija parametara: gradijentni spust.
theta = theta - eta/N * grad;
# Spremimo trenutnu vrijednost funkcije cilja u polje hist.
hist.append( f(theta, x, y) );
return (theta, hist);
theta0 = np.array( [0, 0] );
# Ispobajmo različite veličine koraka.
eta_1 = 0.1; (theta_1, hist_1) = grad_spust( x, y, g, grad_g, theta0, eta_1, 50 );
eta_2 = 0.03; (theta_2, hist_2) = grad_spust( x, y, g, grad_g, theta0, eta_2, 50 );
eta_3 = 0.01; (theta_3, hist_3) = grad_spust( x, y, g, grad_g, theta0, eta_3, 50 );
print( f'Grad. spust za eta={eta_1:.3f} -> theta1 = {theta_1[0]:.8f}, theta2 = {theta_1[1]:.8f}' );
print( f'Grad. spust za eta={eta_2:.3f} -> theta1 = {theta_2[0]:.8f}, theta2 = {theta_2[1]:.8f}' );
print( f'Grad. spust za eta={eta_3:.3f} -> theta1 = {theta_3[0]:.8f}, theta2 = {theta_3[1]:.8f}' );
plt.semilogy( hist_1, label=f'$\\eta={eta_1}$' );
plt.semilogy( hist_2, label=f'$\\eta={eta_2}$' );
plt.semilogy( hist_3, label=f'$\\eta={eta_3}$' );
plt.xlabel( 'epoha' );
plt.ylabel( '$f(\\theta)$' );
plt.legend();
plt.title( 'Gradijentni spust' );
Grad. spust za eta=0.100 -> theta1 = 2.99648865, theta2 = 4.07603619
Grad. spust za eta=0.030 -> theta1 = 2.99197166, theta2 = 3.88636951
Grad. spust za eta=0.010 -> theta1 = 2.95716094, theta2 = 2.56197390
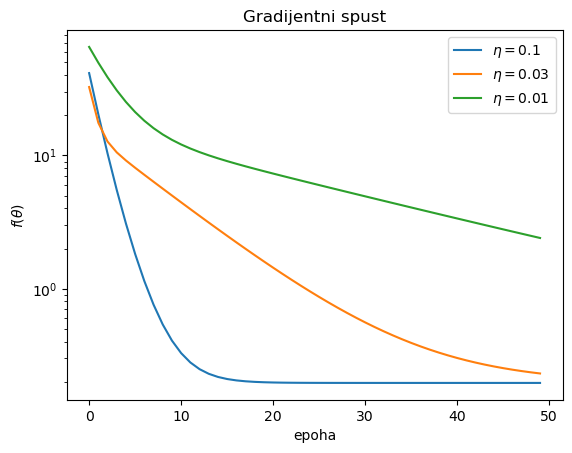
Vidimo ovisnost brzine konvergencije o veličini koraka, koju smo ovdje odabrali metodom pokušaja i pogreške. Da smo uzeli veći korak (npr. \(\eta = 0.5\), probajte!), metoda ne bi uopće konvergirala. Uz premali korak, metoda konvergira sporo. No uz malo eksperimentiranja, izbor npr. \(\eta = 0.1\) vodi do konačne aproksimacije \(\theta_1, \theta_2\) koja je jako blizu egzaktnih vrijednosti \(\theta_1^\ast = 3\), \(\theta_2^\ast = 4\).
Uočimo da ovdje u svakoj iteraciji \(N=100\) puta pozivamo grad_g, pa je ta funkcija ukupno pozvana \(5000\) puta jer računamo \(50\) iteracija, tj. epoha. (Za manji broj iteracija, aproksimacija nije tako dobra, što se ne vidi na gornjem grafu.)
Sada implementiramo stohastički gradijentni spust. Gore smo opisali metodu kod koje slučajno odabiremo index „sa vraćanjem”, tj. može se dogoditi da neki index iskoristimo više puta nego neki drugi. Donja implementacija koja odabire indexe „bez vraćanja” je češća u praksi.
def stoh_grad_spust( x, y, g, grad_g, theta0, eta, n_epoch ):
# Ulaz:
# x = polje točaka u kojima su vršena mjerenja, duljine N
# y = polje izmjerenih vrijednosti za svaku točku iz x
# g = funkcije koja čini jedan pribrojnik funkcije cilja koju treba minimizirati.
# grad_g = funkcija koja računa gradijent od g
# theta0 = početne vrijednosti parametara
# eta = (konstantni) korak u metodi gradijentnog spusta
# n_epoch = broj iteracija koje treba provesti.
# Izlaz:
# theta = vrijednost parametara nakon n_epoch epoha stoh. grad. spusta
# hist = polje vrijednosti funkcije cilja nakon svakog koraka stoh. grad. spusta. Samo za crtanje grafa.
# Broj mjerenja.
N = x.shape[0];
# Početna vrijednost parametara. Prazno polje hist.
theta = theta0; hist = [];
# Iteracije.
for epoch in range( 0, n_epoch ):
# Napravi slučajnu permutaciju ulaznih podataka.
perm = np.random.permutation( N );
x_perm = x[perm];
y_perm = y[perm];
# Protrči kroz sve podatke u permutiranom redoslijedu.
for i in range( 0, N ):
# Izračunaj gradijent funkcije f = g(theta, xperm_i, yperm_i).
grad = grad_g( theta, x_perm[i], y_perm[i] );
# Iduća iteracija parametara: stohastički gradijentni spust.
theta = theta - eta * grad;
# Spremimo trenutnu vrijednost funkcije cilja u polje hist.
hist.append( f(theta, x, y) );
return (theta, hist);
theta0 = np.array( [0, 0] );
# Ispobajmo različite veličine koraka.
eta_1 = 0.02; (theta_1, hist_1) = stoh_grad_spust( x, y, g, grad_g, theta0, eta_1, 10 );
eta_2 = 0.003; (theta_2, hist_2) = stoh_grad_spust( x, y, g, grad_g, theta0, eta_2, 10 );
eta_3 = 0.001; (theta_3, hist_3) = stoh_grad_spust( x, y, g, grad_g, theta0, eta_3, 10 );
print( f'Stoh. grad. spust za eta={eta_1:.3f} -> theta1 = {theta_1[0]:.8f}, theta2 = {theta_1[1]:.8f}' );
print( f'Stoh. grad. spust za eta={eta_2:.3f} -> theta1 = {theta_2[0]:.8f}, theta2 = {theta_2[1]:.8f}' );
print( f'Stoh. grad. spust za eta={eta_3:.3f} -> theta1 = {theta_3[0]:.8f}, theta2 = {theta_3[1]:.8f}' );
plt.semilogy( hist_1, label=f'$\\eta={eta_1}$' );
plt.semilogy( hist_2, label=f'$\\eta={eta_2}$' );
plt.semilogy( hist_3, label=f'$\\eta={eta_3}$' );
plt.xlabel( 'iteracija' );
plt.ylabel( '$f(\\theta)$' );
plt.legend();
plt.title( 'Stohastički gradijentni spust' );
Stoh. grad. spust za eta=0.020 -> theta1 = 3.01721582, theta2 = 4.13496426
Stoh. grad. spust za eta=0.003 -> theta1 = 3.01587964, theta2 = 4.06336625
Stoh. grad. spust za eta=0.001 -> theta1 = 2.97879469, theta2 = 3.52017539
I ovdje smo metodom pokušaja i pogreške odabrali veličinu koraka. Ponovno, za veće koraka metoda ne bi konvergirala. Vidimo da sada konvergencija nije monotona, jer samo jedan slučajno odabrani uzorak ne daje nužno dobru aproksimaciju za gradijent funkcije cilja. S druge strane, sada u svakoj iteraciji imamo samo po jedan poziv funkcije grad_g. Vidimo da dobru aproksimaciju optimalnih parametara \(\theta\) možemo dobiti već sa \(1000\) poziva funkcije grad_g, što je bolje no kod standardnog gradijentnog spusta.
Na kraju, implementiramo i testiramo stohastički gradijentni spust s grupama. Ponovno koristimo tehniku slučajnog izbora „bez vraćanja”.
def stoh_grad_spust_s_grupama( x, y, g, grad_g, theta0, eta, n_epoch, velicina_grupe ):
# Ulaz:
# x = polje točaka u kojima su vršena mjerenja, duljine N
# y = polje izmjerenih vrijednosti za svaku točku iz x
# g = funkcije koja čini jedan pribrojnik funkcije cilja koju treba minimizirati.
# grad_g = funkcija koja računa gradijent od g
# theta0 = početne vrijednosti parametara
# eta = (konstantni) korak u metodi gradijentnog spusta
# n_epoch = broj epoha koje treba provesti.
# velicina_grupe = broj mjerenja koji sudjeluju u jednom koraku gradijentne metode.
# Izlaz:
# theta = vrijednost parametara nakon n_epoch epoha stoh. grad. spusta s grupama.
# hist = polje vrijednosti funkcije cilja nakon svakog koraka stog. grad. spusta s grupama. Samo za crtanje grafa.
# Broj mjerenja.
N = x.shape[0];
# Početna vrijednost parametara. Prazno polje hist.
theta = theta0; hist = [];
# Iteracije.
for epoch in range( 0, n_epoch ):
# Napravi slučajnu permutaciju ulaznih podataka.
perm = np.random.permutation( N );
x_perm = x[perm];
y_perm = y[perm];
for prvi_index in range( 0, N, velicina_grupe ):
# Grupa se sastoji od indexa prvi_index, prvi_index+1, ..., zadnji_index-1.
zadnji_index = min( N, prvi_index + velicina_grupe );
# Izračunaj gradijent funkcije f = 1/velicina_grupe * suma_{i u grupi} g(theta, xperm_i, yperm_i).
grad = np.array( [0, 0] );
for i in range( prvi_index, zadnji_index ):
grad = grad + grad_g( theta, x_perm[i], y_perm[i] );
# Zadnja grupa može biti manja.
velicina_ove_grupe = zadnji_index - prvi_index;
# Iduća iteracija parametara: stohastički gradijentni spust.
theta = theta - eta/velicina_grupe * grad;
# Spremimo trenutnu vrijednost funkcije cilja u polje hist.
hist.append( f(theta, x, y) );
return (theta, hist);
theta0 = np.array( [0, 0] );
# Ispobajmo različite veličine koraka.
eta_1 = 0.1; (theta_1, hist_1) = stoh_grad_spust_s_grupama( x, y, g, grad_g, theta0, eta_1, 6, 10 );
eta_2 = 0.03; (theta_2, hist_2) = stoh_grad_spust_s_grupama( x, y, g, grad_g, theta0, eta_2, 6, 10 );
eta_3 = 0.01; (theta_3, hist_3) = stoh_grad_spust_s_grupama( x, y, g, grad_g, theta0, eta_3, 6, 10 );
print( f'Stoh. grad. spust s grupama veličine 10 za eta={eta_1:.3f} -> theta1 = {theta_1[0]:.8f}, theta2 = {theta_1[1]:.8f}' );
print( f'Stoh. grad. spust s grupama veličine 10 za eta={eta_2:.3f} -> theta1 = {theta_2[0]:.8f}, theta2 = {theta_2[1]:.8f}' );
print( f'Stoh. grad. spust s grupama veličine 10 za eta={eta_3:.3f} -> theta1 = {theta_3[0]:.8f}, theta2 = {theta_3[1]:.8f}' );
plt.semilogy( hist_1, label=f'$\\eta={eta_1}$' );
plt.semilogy( hist_2, label=f'$\\eta={eta_2}$' );
plt.semilogy( hist_3, label=f'$\\eta={eta_3}$' );
plt.xlabel( 'iteracija' );
plt.ylabel( '$f(\\theta)$' );
plt.legend();
plt.title( 'Stohastički gradijentni spust s grupama' );
Stoh. grad. spust s grupama veličine 10 za eta=0.100 -> theta1 = 2.86481456, theta2 = 4.09519100
Stoh. grad. spust s grupama veličine 10 za eta=0.030 -> theta1 = 2.98144293, theta2 = 3.97689768
Stoh. grad. spust s grupama veličine 10 za eta=0.010 -> theta1 = 2.97039296, theta2 = 2.84309984
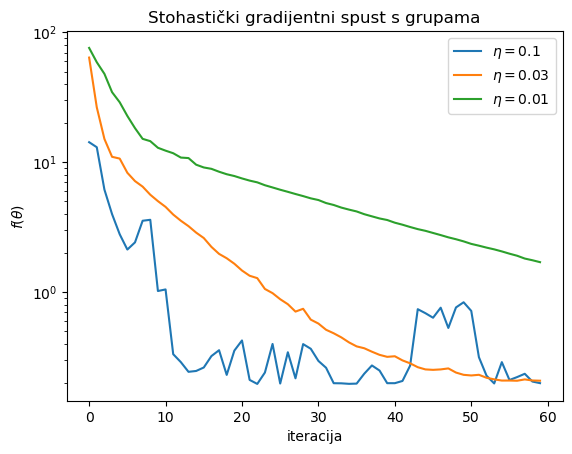
Kod ove metode, konvergencija je ponovno prilično nestabilna za preveliki korak. No za pogodno odabranu veličinu koraka, sada nam treba samo \(600\) poziva funkcije grad_g (jer ih je po \(10\) u svakoj od \(60\) iteracija) da bismo dobili dobru aproksimaciju za optimalni \(\theta\).
Napredniji algoritmi iteriranja
Kako vidimo, sve varijante stohastičkog gradijentnog spusta su dosta osjetljive na izbor veličine koraka. Stoga su razvijene naprednije metode koje taj proces pokušavaju automatizirati i osigurati, barem u praksi, bržu i sigurniju konvergenciju.
Jedna jednostavna tehnika je: ako detektiramo prevelike oscilacije vrijednosti funkcije cilja u zadnjih nekoliko iteracija, onda smanjimo korak \(\eta_k\) (na primjer, s faktorom \(2\)), a ako detektiramo stagnaciju u zadnjih nekoliko iteracija onda povećamo korak \(\eta_k\).
Naprednije tehnike uključuju korištenje tzv. momenta: novi smjer \(d^{(k)}\) osim \(\nabla f(\theta^{(k)})\) zadržava i manju komponentu u ranije korištenim smjerovima \(d^{(k-1)}\), \(d^{(k-2)}\), itd. Trenutno najpopularnija takva metoda je ADAM (Adaptive Moment Estimation). Kratki pregled takvih metoda možete vidjeti ovdje.
Detaljnije objašnjenje gore opisanih algoritama može se vidjeti npr. ovdje. Analiza konvergencije je vrlo netrivijalna i još uvijek u razvoju. Neki rezultati se mogu pronaći u Poglavlju 5 knjige Francisa Bacha Learning Theory from First Principles.