Show code cell source
import matplotlib.pyplot as plt;
import math;
%matplotlib inline
5.1. Numerička derivacija#
Opis problema. Za zadanu dovoljno glatku funkciju \(f:\langle a,b \rangle \to \R\) i točku \(x_0 \in \langle a,b \rangle\) želimo odrediti aproksimaciju prve derivacije \(f'(x_0)\), ili općenito vrijednost \(k\)-te derivacije \(f^{(k)}(x_0)\), za \(k \in \N\).
Motivirani smo slično kao u problemima interpolacije: ili je djelovanje funkcije \(f\) poznato na cijeloj svojoj domeni, no ne znamo njenu analitičku definiciju kako bismo izračunali derivaciju, ili je djelovanje funkcije \(f\) poznato samo u nekim točkama domene, pa derivaciju očito možemo samo aproksimirati.
Kada bismo sami morali aproksimirati derivaciju funkcije u nekoj točki, znajući definiciju derivacije, pokušali bismo umjesto derivacije računati neku podijeljenu razliku \(\dfrac{f(x)-f(y)}{x-y}\) za točke \(x,y \in \langle a,b \rangle\) bliske točki u kojoj derivaciju računamo. Intuicija nam je ispravna, te ćemo je potvrditi u nastavku. Također, intuicija nam kaže da što su \(x\) i \(y\) bliži točki kojoj želimo izračunati vrijednost derivacije, da će aproksimacija biti točna, što je samo djelomično točno, što ćemo vidjeti na kraju ove lekcije.
Napomenimo još da se u praksi rijetko traži račun za derivaciju za \(k\geq 4\), a ovdje ćemo prikazati neke aproksimacije prve i druge derivacije.
U prošlim poglavljima naučili smo da interpolacijski polinom dobro opisuje ponašanje neke funkcije \(f\) (znamo i ocjenu pogreške interpolacije). Zato je za očekivati da će slično biti i za derivaciju. Dakle, veliku familiju formula za numeričku derivaciju možemo dobiti derivirajući odgovarajući interpolacijski polinom za funkciju \(f\).
Uzmimo derivabilnu funkciju \(f: \langle a,b \rangle \to \R\) i dvije točke \(a<x_0<x_1<b\). Odredimo interpolacijski polinom prvog stupnja za funkciju \(f\) i točke \(x_0\) i \(x_1\), te ga iskoristimo za aproksimaciju derivacije. Interpolacijski polinom možemo naći koristeći njegov Newtonov zapis.
Interpolacijski polinom glasi
a njegova derivacija je konstanta na cijelom \(\R\) i iznosi
Dakle, za svaku točku iz \(x \in \langle a, b \rangle\) možemo aproksimirati vrijednost \(f'(x)\) vrijednošću \(\dfrac{f(x_1)-f(x_0)}{x_1-x_0}\). Taj broj zvat ćemo drugim imenom ovisno za koju točku domene to napravimo.
Za derivabilnu funkciju \(f:\langle a,b \rangle \to \R\) i dvije točke \(a<x_0<x_1<b\), aproksimacija prve derivacije
naziva se podijeljena razlika unaprijed, aproksimacija
naziva se podijeljena razlika unazad, a aproksimacija
gdje je \(x' \in \langle x_0, x_1 \rangle\), naziva se središnja podijeljena razlika.
Iako je riječ o istoj formuli primijenjenoj za različite točke domene, imena aproksimacija došle su iz činjenice da za račun derivacije u nekoj fiksnoj točki trebamo dodatnu informaciju o nekoj točki desno („unaprijed”) ili lijevo („unazad”) od te same točke, ili obje. Središnju podijeljenu razliku možemo raditi za bilo koju točku iz intervala \(\langle x_0, x_1 \rangle\), no najlogičnije ju je raditi za polovište intervala (ali i najbolje, što ćemo vidjeti u nastavku).
Uzmimo derivabilnu funkciju \(f: \langle a,b \rangle \to \R\) i tri točke \(a<x_{-1}< x_0<x_1<b\) uz \(x_1 - x_0 = x_0 - x_{-1} =: h\). Odredimo interpolacijski polinom drugog stupnja za funkciju \(f\) i točke \(x_{-1}\), \(x_0\) i \(x_1\), te ga iskoristimo za aproksimaciju derivacije. Interpolacijski polinom ponovno tražimo koristeći Newtonovu bazu.
Interpolacijski polinom glasi
a njegova derivacija
Uvrstimo u nju neke posebne vrijednosti. Za \(x=x_0\) dobivamo
što je upravo središnja podijeljena razlika (udaljenost točaka \(x_1\) i \(x_{-1}\) sada je \(2h\)). Budući da smo središnju podijeljenu razliku za \(x_0\) dobili iz aproksimacije funkcije polinomom drugim stupnjem, imamo razloga vjerovati da će se ta aproksimacija ponašati bolje, odnosno da će imati bolju ocjenu pogreške od svih ostalih aproksimacija dobivenih u prošlom primjeru.
Uvrstimo li u \(p_2'(x)\) točku \(x=x_{-1}\), dobivamo
Ovo je prva formula koja nije intuitivna. Korisna je jer je dobivena kao aproksimacija derivacije polinomom drugog stupnja (dakle, očekujemo bolju ocjenu pogreške), u slučajevima kada računamo vrijednost derivacije u točki za koju imamo dodatne podatke o vrijednosti funkcije samo s jedne strane te točke. Slično bismo dobili za \(f'(x_1)\).
Ako je funkcija \(f\) dvaput derivabilna, interpolacijski polinom \(p_2\) možemo iskoristiti za aproksimaciju druge derivacije. Za svaku točku domene \(x\) vrijedi
Usporedimo na primjeru središnju podijeljenu razliku i podijeljenu razliku unaprijed u Pythonu i potvrdimo slutnju da će se središnja podijeljena razlika ponašati bolje. Neka je \(f(x)=\log_2 x\), računajmo derivaciju te funkcije u točki \(x_0=3\) i usporedimo numeričku izračunatu vrijednost s točnom vrijednosti \(f'(x_0) = \dfrac{1}{3 \ln 2}\). Uspoređujemo vrijednosti za \(h\)-ove oblika za \(h=2^{-k}\), \(k = 1,\dots, 14\).
Show code cell source
def PrimjerNumerickeDerivacije (h_ovi, metoda = 0):
# Prima polje različitih vrijednosti od h i varijablu "metoda" kojom biramo metodu:
# - središnju podijeljenu razliku (ako metoda = 0).
# - podijeljenu razliku unaprijed (ako metoda = 1).
# Za svaki h, određuje se apsolutna greška prilikom aproksimacije derivacije funkcije
# log_2(x) odabranom metodom u x0=3 za taj h.
# Funkcija vraća polje dobivenih grešaka.
N = len(h_ovi)
greske = [0] * N
x0 = 3
prava_vrijednost = 1. / (x0 * math.log(2))
for i in range(N):
h = h_ovi[i]
if metoda == 0:
# središnja podijeljena razlika
aprox_vrijednost = (math.log(x0 + h, 2) - math.log(x0 - h, 2)) / (2 * h)
else:
# podijeljena razlika unaprijed
aprox_vrijednost = (math.log(x0 + h, 2) - math.log(x0, 2)) / h
greske[i] = abs(aprox_vrijednost - prava_vrijednost)
return greske
h_ovi = [2 ** (-broj) for broj in range(0, 14)]
greske_sred = PrimjerNumerickeDerivacije(h_ovi, 0)
greske_napr = PrimjerNumerickeDerivacije(h_ovi, 1)
fig = plt.figure(figsize=[16, 5])
ax1 = fig.add_subplot(121)
ax1.title.set_text(f'Graf greške numeričke derivacije')
ax1.plot(h_ovi, greske_sred, marker='o', color='b', label='središnja podijeljena razlika')
ax1.plot(h_ovi, greske_napr, marker='o', color='r', label='podijeljena razlika unaprijed')
plt.xlabel( 'h' )
plt.ylabel( 'greška E(h)' )
plt.legend()
ax1 = fig.add_subplot(122)
ax1.title.set_text(f'Log-log graf greške numeričke derivacije')
plt.loglog(h_ovi, greske_sred, marker='o', color='b', label='središnja podijeljena razlika')
plt.loglog(h_ovi, greske_napr, marker='o', color='r', label='podijeljena razlika unaprijed')
plt.xlabel( 'h' )
plt.ylabel( 'greška E(h)' )
plt.legend()
plt.show()
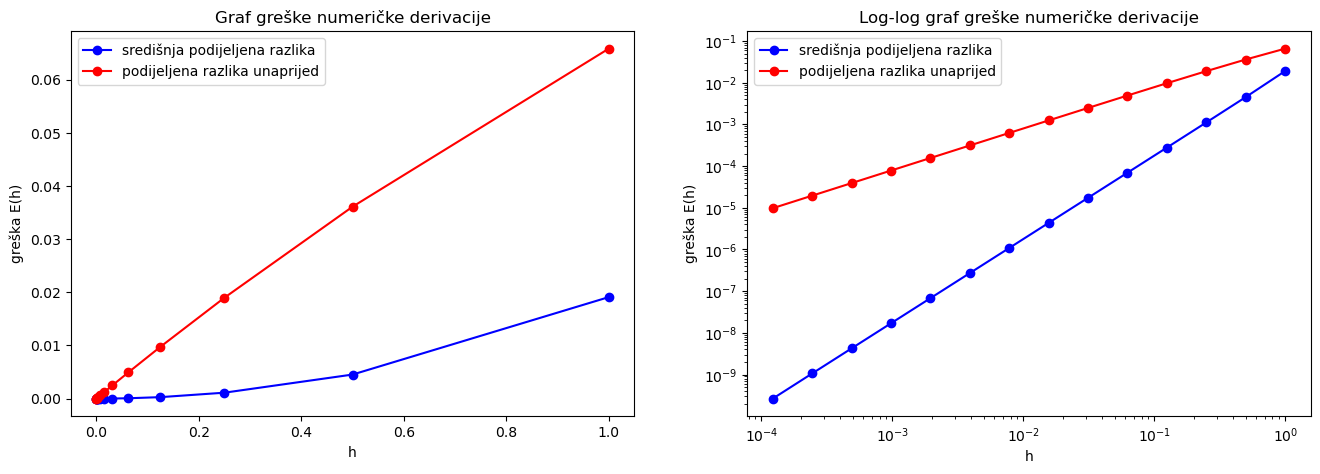
Lijevo su nacrtani grafovi grešaka za dvije metode koje smo uspoređivali. Vidimo da je plavi graf ispod crvenog, što znači da središnjom podijeljenom razlikom dobivamo manju grešku nego podijeljenom razlikom unaprijed. Međutim, za jako male \(h\) (donji lijevi kut lijevog grafa) točke su se nagurale i ne vidimo jasno što se događa na slici, primjerice, ne vidimo je li možda crveni graf pao ispod plavog. Zato se u numeričkoj matematici često crta tzv. log-log graf (desno). Na takvom grafu na \(x\)-os stavljamo logaritmirane vrijednosti domene, a na \(y\)-os logaritmirane vrijednosti kodomene (u bazi \(10\)). I dalje o konvergenciji govori ponašanje grafova kada \(x\)-ovi idu prema lijevo, i dalje je plavi graf „bolji”.
Dodatno, log-log graf je bogatiji u smislu da se s njega može vidjeti i red konvergencije. Objasnimo to detaljnije. Neka za neki \(h\) vrijednost \(E(h)\) označava apsolutnu grešku računa numeričke derivacije. Kako oba grafa na desnoj slici izgledaju kao pravci, te kako se radi o log-log grafovima, možemo reći da za svaki od njih postoje konstante \(a\) i \(b\) takve da je
Sređivanjem dobivamo
uz \(B:=10^b\). Dakle, nagib pravca \(a\) s log-log grafa zapravo je jednak eksponentu \(a\) u formuli \(E(h) \approx B \cdot h^a\), a to je upravo jednako redu konvergencije te metode. S ovog grafa možemo izmjeriti redove konvergencije i vidjeti da bi za središnju podijeljenu razliku red trebao biti jednak \(2\), a za podijeljenu razliku unaprijed red trebao biti jednak \(1\).
Ocjena pogreške za aproksimaciju derivacije#
Kako sve gornje aproksimacije derivacije proizlaze iz odgovarajućeg interpolacijskog polinoma, i ocjene pogreške dobit ćemo iz rezultata za ocjenu pogreške interpolacijskog polinoma. Imamo dva rezultata koja možemo koristiti: Teorem 3.10 ili Teorem 3.12. U oba slučaja tvrdnju teorema bismo derivirali s obje strane kako bismo na lijevoj strani dobili razliku derivacija koju možemo ocijeniti. No, u Teoremu 3.10 na desnoj strani imamo izraz koji za svaki \(x\) ovisi o nekom \(\xi\) koji ovisi o tom \(x\) na nepoznat način, te taj izraz ne možemo derivirati. Zato nužno koristimo Teorem 3.12.
Pretpostavimo:
funkcija \(f\) ima \((n+2)\)-u derivaciju na segmentu \([a, b]\);
čvorovi interpolacije \(x_0, \ldots, x_n \in [a, b]\) su međusobno različiti.
Neka je \(p_n\) interpolacijski polinom za \(f\) stupnja \(n\). Tada za svaku točku \(x \in [a, b]\), postoje \(\xi_1, \xi_2\) iz intervala \(\langle x_{min}, x_{max} \rangle\), uz
te da za grešku derivacije interpolacijskog polinoma u točki \(x\) vrijedi
Kao i u prije:
nazivamo polinom čvorova.
Primjenom Teorema 3.12 dobivamo
Derivirajmo obje strane jednakosti. Na lijevoj strani dobivamo \(e'(x)\), a na desnoj koristimo Propoziciju 3.15. Dobivamo
Koristeći za svaku podijeljenu razliku na desnoj strani jednakosti Propoziciju 3.13, dobivamo traženu tvrdnju.
Ako derivaciju aproksimiramo u nekoj od točaka interpolacije, član \(\omega(x)\) u gornjem teoremu nestaje. Kako za funkciju koja je \((n+2)\) puta derivabilna vrijedi da joj je \((n+1)\)-a derivacija neprekidna, lako dobivamo sljedeći rezultat.
Pretpostavimo:
funkcija \(f\) ima \((n+2)\)-u derivaciju na segmentu \([a, b]\);
čvorovi interpolacije \(x_0, \ldots, x_n \in [a, b]\) su međusobno različiti.
Neka je \(p_n\) interpolacijski polinom za \(f\) stupnja \(n\). Tada za grešku interpolacijskog polinoma u bilo kojoj točki \(x_i\) (\(i=0,\dots,n\)) vrijedi
gdje je \(M_{n+1} := \max_{x \in [a, b]} |f^{(n+1)}(x)|\).
Napomena
Primijetimo da u gornjem korolaru sami rezultat ne traži da funkcija \(f\) ima \((n+2)\)-u derivaciju, no ta pretpostavka je nužna jer koristimo rezultat Teorema 5.4.
Ocijenimo sada prethodno izračunate numeričke derivacije.
Neka je \(f\) triput derivabilna na \([a,b]\) i neka su dane dvije točke \(a<x_0<x_1<b\). Za pogrešku podijeljenih razlika unaprijed i unazad vrijedi
gdje je \(h:=x_1-x_0\).
Neka je \(p_1(x)\) interpolacijski polinom prvog stupnja za \(f\) kroz točke \(x_0\) i \(x_1\). Za polinom čvorova \(\omega = (x-x_0) (x-x_1)\) vrijedi
pa je \(|\omega'(x_0)| = |\omega'(x_1)| = h \). Primijenjujući Korolar 5.5 dobivamo da za podijeljene razlike unaprijed i unazad vrijedi
Neka je \(f\) četiri puta derivabilna na \([a,b]\) i neka su dane točke \(a<x_{-1}< x_0<x_1<b\) uz \(x_1 - x_0 = x_0 - x_{-1} =: h\). Za pogrešku središnje podijeljene razlike vrijedi
Ovaj i prošli korolar potvrđuju naše slutnje iz primjera u Pythonu.
Neka je \(p_2(x)\) interpolacijski polinom drugog stupnja za \(f\) kroz točke \(x_{-1}\), \(x_0\) i \(x_1\). Za polinom čvorova
vrijedi \(\omega ' (x) = 3(x-x_0)^2 - h^2\), pa je \(|\omega'(x_0)| = h^2 \). Primijenjujući Korolar 5.5 dobivamo da za središnju podijeljenu razliku vrijedi
Ocjenu pogreške za središnju podijeljenu razliku možemo dobiti i iz Teorema 5.4 ako uvrstimo točku koja nije čvor interpolacije. Na takav način možemo izvesti ocjenu pogreške za tu podijeljenu razliku za proizvoljnu točku \(x \in \langle x_{0}, x_1\rangle\), no samo za \(x=x_0\) dobili bismo ocjenu pogreške reda \(\mathcal O (h^2)\). Nadalje, isti Teorem 5.4 može se generalizirati i za više derivacije. Pokušajte dokazati da za aproksimaciju druge derivacije
vrijedi ocjena greške
Problem s malim \(h\)#
Vratimo se na primjer u Pythonu, i pokušajmo još smanjiti \(h\). Dakle, pogledajmo formule za \(h=2^{-k}\), \(k = 1,\dots, 50\) (umjesto \(14\) kao prije).
Show code cell source
h_ovi = [2 ** (-broj) for broj in range(0, 50)]
greske_sred = PrimjerNumerickeDerivacije(h_ovi, 0)
greske_napr = PrimjerNumerickeDerivacije(h_ovi, 1)
fig = plt.figure(figsize=[16, 5])
ax1 = fig.add_subplot(121)
ax1.title.set_text(f'Graf greške numeričke derivacije')
ax1.plot(h_ovi, greske_sred, marker='o', color='b', label='središnja podijeljena razlika')
ax1.plot(h_ovi, greske_napr, marker='o', color='r', label='podijeljena razlika unaprijed')
plt.xlabel( 'h' );
plt.ylabel( 'greška E(h)' );
plt.legend()
ax1 = fig.add_subplot(122)
ax1.title.set_text(f'Log-log graf greške numeričke derivacije')
plt.loglog(h_ovi, greske_sred, marker='o', color='b', label='središnja podijeljena razlika')
plt.loglog(h_ovi, greske_napr, marker='o', color='r', label='podijeljena razlika unaprijed')
plt.xlabel( 'h' );
plt.ylabel( 'greška E(h)' );
plt.legend()
plt.show()
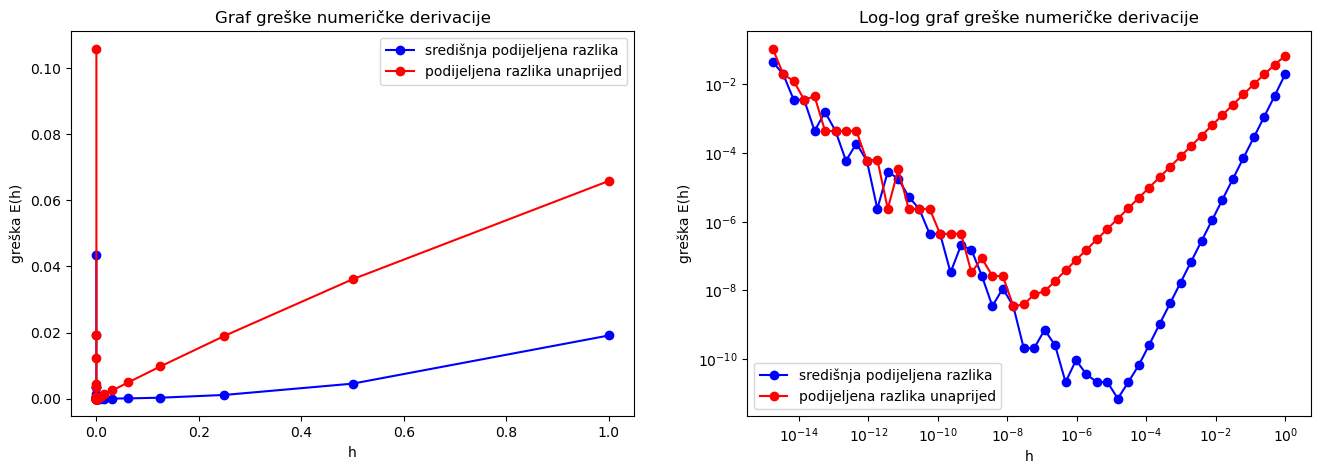
Intuicija, ili definicija derivacije preko limesa, ili ocjene pogreške za podijeljene razlike, sve to govori nam da što je manji \(h\) svaka od podijeljenih razlika treba biti bolja aproksimacija za samu derivaciju, no iz gornjih računa vidimo da to nije tako. Razlog leži u grešci zaokruživanja. Naime, što je razlika točaka \(x\) i \(y\) manja, u brojniku izraza
nalazi se razlika sve bližih brojeva (nužno razlika tih brojeva ide k nuli zbog neprekidnosti funkcije \(f\)), što znači da dolazi do opasnog kraćenja.
Provedimo detaljniju analizu na primjeru središnje podijeljene razlike. Pretpostavimo da se prilikom izračuna vrijednosti \(f(x_{-1})\) i \(f(x_1)\) dogodila (apsolutna) greška zaokruživanja \(\varepsilon_{-1}\) i \(\varepsilon_{1}\) redom, uz \(|\varepsilon_{-1}|,|\varepsilon_{1}| \leq \varepsilon\), odnosno da su u računalu pohranjene vrijednosti
Stoga je greška u aproksimaciji derivacije izračunate na računalu umjesto \(f'(x_0) - \frac{f(x_{-1}) - f(x_{1})}{2h}\) zapravo jednaka
Radi jednostavnosti, pretpostavimo dodatno da je greška dijeljenja u kvocijentu \(\dfrac{\hat{f}_{-1}-\hat{f}_{1}}{2h}\) zanemariva, te da svi brojevi (uključujući i \(h\)) prikazivi u računalu. Grešci sada doprinose član \(e'(x_0)\), koji smo ocijenili s \(\dfrac{h^2}{6} M_{3}\), te član \(\dfrac{\varepsilon_{-1} - \varepsilon_1}{2h}\), koji možemo ocijeniti kao
Dakle, dobili smo da je greška u aproksimaciji derivacije izračunate na računalu ocijenjena s
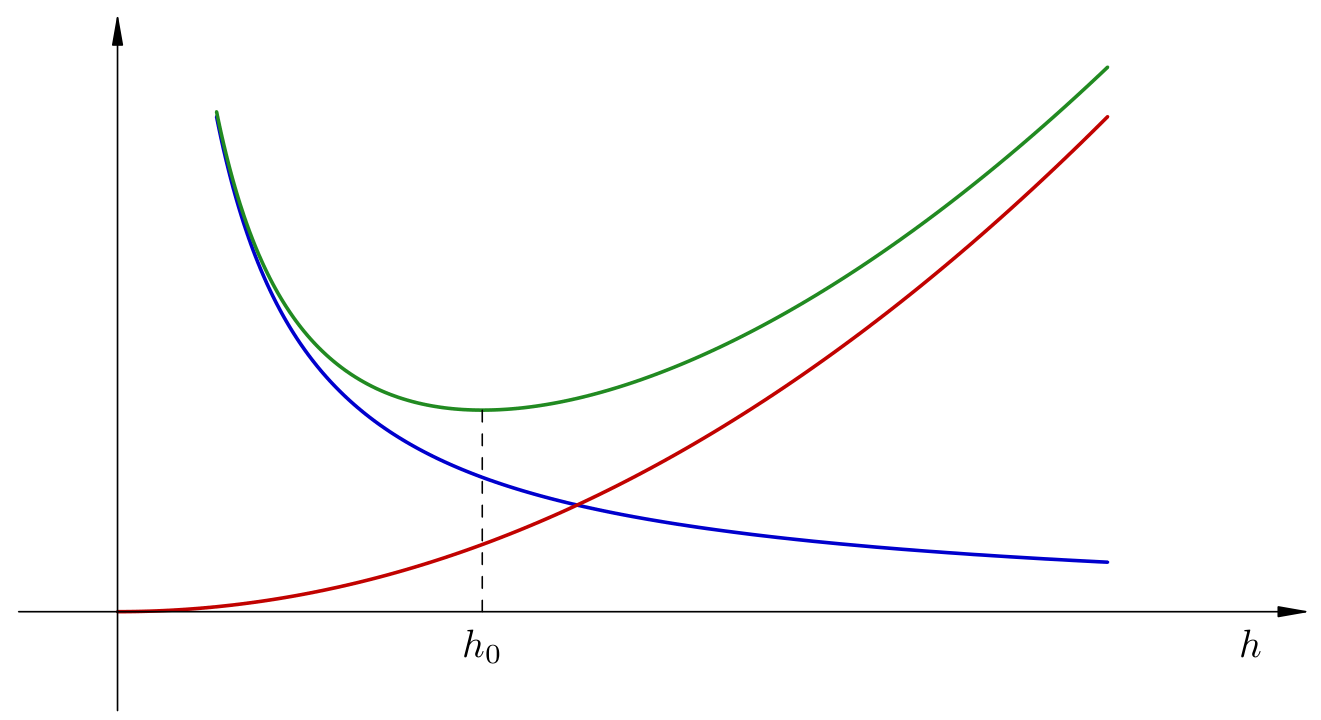
Sjetimo se, ovdje utječemo samo na vrijednost varijable \(h\), broj \(\varepsilon\) je fiksan. Problem koji smo vidjeli u praksi sada vidimo i analitički: kada \(h\) teži k nuli, prvi član teži k nuli, no drugi teži u beskonačnost. Zato \(h\) ne smije biti premalen. S druge strane, ne smije biti ni prevelik, jer ćemo dobiti preveliku grešku u prvom članu. Ovu pogrešku možemo i skicirati (ispod). Crvenom bojom nacrtan je graf \(h\mapsto \dfrac{h^2}{6} M_{3}\) koji dolazi zbog greške numeričke derivacije, plavom bojom označen je graf funkcije \(h \mapsto \dfrac{\varepsilon}{h}\) koji dolazi zbog greške u aritmetici računala, a zelenom bojom je zbroj tih funkcija. Sa slike vidimo da za račun numeričke derivacije postoji optimalan \(h_0\) za koji je račun numeričke derivacije najtočniji, ali da ne postoji način da ta greška konvergira u nulu na neki način kada mijenjamo \(h\), odnosno da veću točnost ne možemo u pravilu postići.
Lako je odrediti minimum funkcije \(h \mapsto \dfrac{h^2}{6} M_{3} + \dfrac{\varepsilon}{h}\); on se postiže za \(h_0 = \sqrt[3]{\frac{3\eps}{M_3}}\). I zaista, u praksi se u slučaju središnje podijeljene razlike tipično uzima \(h \sim \sqrt[3]{u}\), gdje je \(u\) jedinična greška zaokruživanja. Za podijeljene razlike unaprijed ili unazad se uzima \(h \sim \sqrt{u}\). (Optimalna vrijednost naravno ovisi i o funkciji \(f\); ovo je u slučaju da nemamo dodatne informacije o \(f\).)
Iz tog razloga je račun numeričke derivacije u praksi netrivijalan problem, te je zato u kompleksnijim problemima koji traže deriviranje bolje izbjeći numeričko deriviranje.
Automatsko diferenciranje
U nekim situacijama, na računalu je moguće provesti egzaktno računanje derivacija ili gradijenata proizvoljno složenih funkcija. Na primjer, u Pythonu napišemo bilo kakvu funkciju \(f\) koja kao argument prima vektor realnih brojeva \(x\); unutar \(f\) možemo imati for-petlje, grananje, bilo kakve matematičke operacije nad \(x\). Postoje specijalne biblioteke za tzv. automatsko diferenciranje koje su u stanju izračunati egzaktni gradijent \(\nabla f(x_0)\) u bilo kojoj točki \(x_0\). To je posebno važno kod strojnog učenja i neuronskih mreža, kod kojih je (automatsko) deriviranje ključna faza u procesu minimizacije funkcije cilja. Primjeri takvih biblioteka su JAX ili autograd unutar PyTorch-a.
No numerička derivacija i dalje ima vrlo važnu ulogu, između ostalog i kao alat pomoću kojeg izvodimo metode za rješavanje diferencijalnih jednadžbi, kao što ćemo uskoro vidjeti.