Numerička integracija

Sadržaj

5.2. Numerička integracija#

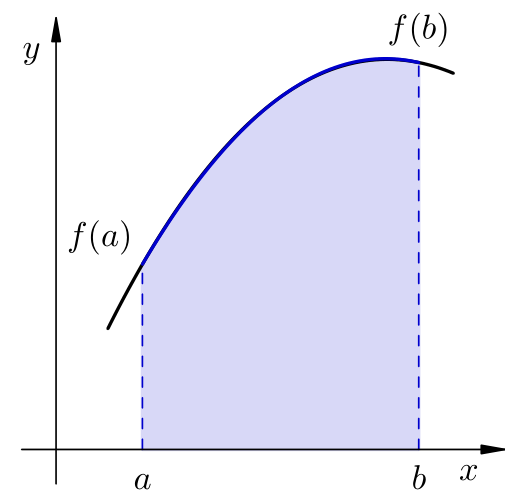
Opis problema. Za zadanu neprekidnu funkciju \(f:[a,b] \to \R \) cilj je numerički odrediti određeni integral \(\displaystyle \int_a^b f(x) dx\).

Motivirani smo slično kao u prošlim lekcijama: ili je funkcija \(f\) dana kao rezultat mjerenja u diskretno mnogo točaka, pa je integral nemoguće odrediti analitički, ili je funkcija \(f\) dana analitičkom fomulom i to u svakoj točki domene \([a,b]\), ali ne postoji zatvorena formula za taj određeni integral, što znači da ovaj rezultat možemo samo aproksimirati.

I ovdje koristimo interpolacijski polinom kao alat: željenu funkciju \(f\) pod integralom možemo zamijeniti odgovarajućim interpolacijskim polinomom, te se nadamo da je integral tog interpolacijskog polinoma (koji znamo izračunati eksplicitno) dovoljno blizu vrijednosti koje želimo aproksimirati.

Pokazat ćemo dvije familije integralnih formula. Kod prvih će mreža točaka u domeni u kojima izvrednjavamo funkciju \(f\) biti uniformno distribuirana, dok u drugim formulama sami biramo mrežu točaka u domeni, nadajući se da ćemo time popraviti točnost formula.

Newton-Cotesove formule#

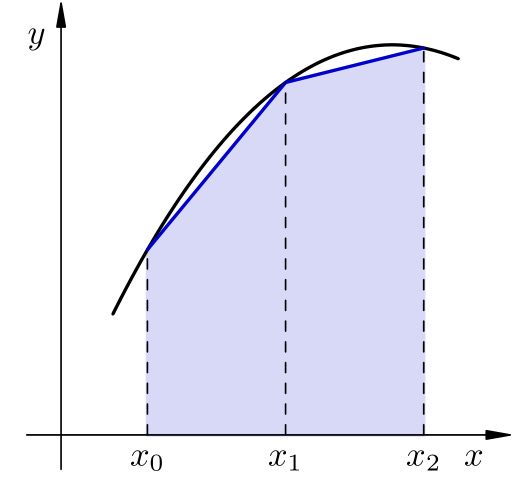
Neka je zadan prirodan broj \(n\) i subdivizija domene \(a=x_0 < x_1< \dots < x_n = b\) uz \(x_{i+1} - x_{i} = h = \frac{b-a}{n}\). Integral funkcije \(f:[a,b] \to \R\) zamijenit ćemo integralom interpolacijskog polinoma \(p_n\) stupnja \(n\) na toj mreži.

Koristeći Lagrangeovu bazu polinoma \(\{\ell_0, \dots, \ell_n \}\),

\[\ell_k(x) = \frac{(x-x_0)(x-x_1)\cdots (x-x_{k-1})(x-x_{k+1}) \cdots (x-x_n)}{(x_k-x_0)(x_k-x_1)\cdots (x_k-x_{k-1})(x_k-x_{k+1}) \cdots (x_k-x_n)} =: \frac{\omega_k(x)}{\omega_k(x_k)}\]

i svojstvo te baze da se interpolacijski polinom \(p_n\) za čvorove \((x_i,f(x_i))\), \(i=0,1,\dots,n\) može zapisati kao

\[p_n(x) = \sum_{i=0}^n f(x_i) \ell_i(x),\]

slijedi

\[\int_a^b f(x) dx \approx \int_a^b p_n(x) dx = \int_a^b \sum_{i=0}^n f(x_i) \ell_i(x) dx = \sum_{i=0}^n f(x_i) \int_a^b \ell_i(x) dx.\]

Dakle, dobili smo integracijsku formulu oblika

\[\int_a^b f(x) dx \approx \sum_{i=0}^n w_i f(x_i) dx,\]

gdje su

\[w_i := \int_a^b \ell_i(x) dx, \quad i=0,1,\dots,n \]

težine integracijske formule, a \(x_0, x_1, \ldots, x_n\) čvorovi integracijske formule. Za pojedini \(n\in \N\) preostalo je izračunati te težine prema gornjoj formuli. To ćemo napraviti za \(n=0,1,2\).

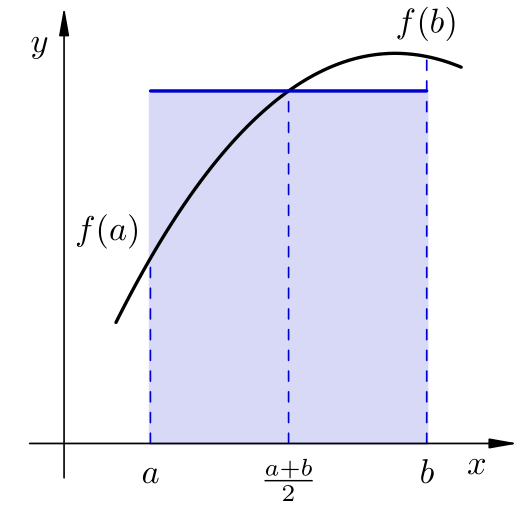
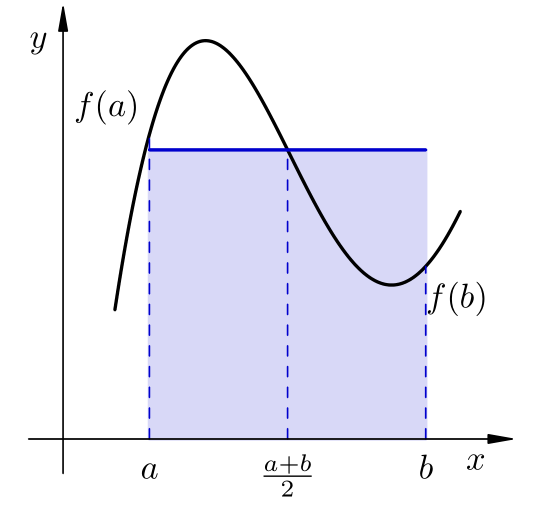
Za \(n=0\), jedini polinom Lagrangeove baze je \(\ell_0 (x) = 1\), pa je \(w_0 = h\). Ako za jedinu točku mreže uzmemo polovište segmenta \([a,b]\), tj. stavimo \(x_0 = \frac{a+b}{2}\), dobivamo sljedeću definiciju.

Definicija 5.8 (Formula srednje točke)

Formula

\[\int_a^b f(x) \ dx \approx I_0(f) := h f\left( \dfrac {a+b}{2} \right)\]

naziva se formula srednje točke (eng. midpoint formula).

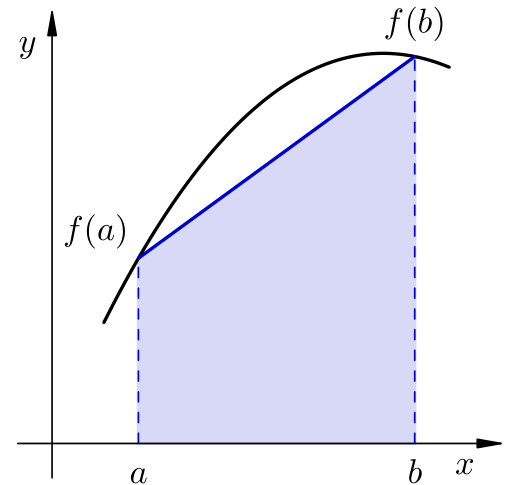
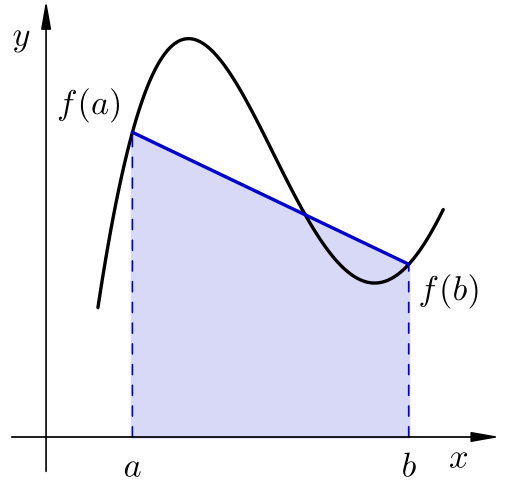
Za \(n=1\), čvorovi su \(x_0=a\) i \(x_1=b\), a polinomi Lagrangeove baze su \(\ell_0(x) = \dfrac{x-b}{h}\), \(\ell_1(x) = \dfrac{a-x}{h}\). Za težinu \(w_0\) vrijedi

\[w_0 = \int_a^b \ell_0 (x) dx = \left( \frac{(x-b)^2}{2h} \right)\Bigg|_{a}^b = \frac{h}{2},\]

a zbog simetrije isti rezultat vrijedi i za \(w_1\). Dobili smo sljedeću formulu:

Definicija 5.9 (Trapezna formula)

Formula

\[\int_a^b f(x) \ dx \approx I_1(f) := \frac h2 \left(f(a) + f(b) \right)\]

naziva se trapezna formula.

Ime je dobila zato što integral aproksimiramo površinom trapeza s vrhovima \((a,f(a))\), \((a,0)\), \((b,0)\) i \((b,f(b))\).

Za \(n=2\) ponavljamo isti postupak koji postaje sve duži. Označimo li s \(\psi(x):=x-\frac{a+b}{2}\), elementi Lagrangeove baze su

\[\begin{split}\begin{align*} \ell_0 (x) &= \frac{\left(x-\dfrac{a+b}{2}\right)(x-b)}{\left(a-\dfrac{a+b}{2}\right)(a-b)} = \frac{2}{h^2} \left(x-\dfrac{a+b}{2}\right)\left(x-b\pm\dfrac{a+b}{2}\right) = \frac{2}{h^2}\psi(x)^2 - \frac{1}{h}\psi(x); \\ \ell_1 (x) &= \frac{\left(x-a\right)(x-b)}{\left(\dfrac{a+b}{2}-a\right)\left(\dfrac{a+b}{2}-b\right)} = -\frac{4}{h^2}\psi(x)^2 +1; \\ \ell_2 (x) &= \frac{(x-a)\left(x-\dfrac{a+b}{2}\right)}{(b-a)\left(b-\dfrac{a+b}{2}\right)} = \frac{2}{h^2}\psi(x)^2 + \frac{1}{h}\psi(x). \end{align*}\end{split}\]

Koristeći

\[\int_a^b \psi(x) \ dx =\int_a^b \left( x-\frac{a+b}{2}\right) \ dx = 0, \quad \int_a^b \psi(x)^2 \ dx= \int_a^b \left( x-\frac{a+b}{2}\right)^2\ dx = \frac{h^3}{12},\]

iz formula \(\displaystyle w_i = \int_a^b \ell_i (x) dx\) dobivamo težine \(w_0 = w_2 = \frac{h}{6}\), \(w_1 = \frac{2h}{3}\).

Definicija 5.10 (Simpsonova formula)

Formula

\[\int_a^b f(x) \ dx \approx I_2(f) := \frac h6 \left(f(a) + 4f\left(\frac {a+b}{2} \right) + f(b) \right)\]

naziva se Simpsonova formula.

Ovaj postupak možemo nastaviti i za ostale \(n\): integral od \(f\) aproksimiramo integralom interpolacijskog polinoma \(p_n\) u ekvidistantnim čvorovima na cijelom segmentu \([a,b]\). Općenito sve formule dobivene na ovaj način pripadaju familiji (zatvorenih) Newton-Cotesovih formula.

Budući da su formule nastale tako što smo integrand zamijenili odgovarajućim interpolacijskim polinomom, možemo zaključiti da je Newton-Cotesova integracijska formula reda \(n\) egzaktna na polinomima stupnja manjim ili jednakim \(n\), tj. da na toj famliji funkcija ovim formulama ne činimo grešku.

Definicija 5.11

Polinomijalni stupanj egzaktnosti integracijske formule \(I(f)\) na intervalu \([a,b]\) definira se kao najveći prirodan broj \(m\) takav da vrijedi

\[\int_a^b p(x) dx = I (p)\]

za sve polinome stupnja \(p\) stupnja manjeg ili jednakog \(m\).

Iz konstrukcije se vidi da izvedene Newton-Cotesove formule s \(n+1\) čvorom imaju stupanj egzaktnosti barem \(n\). Može se dokazati da su i jedine takve formule.

Teorem 5.12

Integracijska formula

\[\int_a^b f(x) \ dx \approx I_n(f) = \sum_{k = 0}^{n} w_k f(x_k)\]

ima polinomijalni stupanj egzaktnosti (barem) \(n\) ako i samo ako je za svaku funkciju \(f:[a,b]\to \R\)

\[I_n(f) = \int_a^b p_{n,f}(x) \ dx,\]

gdje je \(p_{n,f}\) interpolacijski polinom za funkciju \(f\) u čvorovima \(x_0,x_1,\dots,x_n\), odnosno ako i samo ako za težine \(w_0,w_1,\dots,w_n\) vrijedi

\[w_k = \int_a^b \ell_k (x) dx, \quad k=0,1,\dots,n,\]

gdje je \(\ell_k\) \(k\)-ti polinom Lagrangeove baze za čvorove \(x_0,x_1,\dots,x_n\).

Dokaz.

Potrebno je dokazati ekvivalenciju triju tvrdnji:

\[\begin{split}\begin{align*} (A)& \quad I_n(f) \text{ ima stupanj egzaktnosti barem } n;\\ (B)& \quad I_n(f) = \int_a^b p_{n,f}(x) \ dx, \quad \forall f;\\ (C)& \quad w_k = \int_a^b \ell_k (x) \ dx, \quad k=0,1,\dots,n.\\ \end{align*}\end{split}\]

Dokazat ćemo \((C) \Rightarrow (B)\), \((B) \Rightarrow (A)\) i \((A) \Rightarrow (C)\).

Korak 1. Neka su težine \(w_k\) dane kao u \((C)\) i uzmimo proizvoljnu integrabilnu funkciju \(f:[a,b]\to \R\). Kako je \(p_{n,f}\) interpolacijski polinom za \(f\), za njega vrijedi

\[ p_{n,f}(x) = \sum_{k = 0}^{n} f(x_k) \ell_k(x).\]

Koristeći definiciju integracijske formule i čvorova \(w_k\), dobivamo

\[\begin{split}\begin{align*} I_n(f) & = \sum_{k = 0}^{n} w_k f(x_k) = \sum_{k = 0}^{n} f(x_k) \int_a^b \ell_k(x) \ dx \\ & = \int_a^b \left( \sum_{k = 0}^{n} f(x_k) \ell_k(x) \right) \, dx = \int_a^b p_{n,f}(x) \ dx, \end{align*}\end{split}\]

što dokazuje \((B)\).

Korak 2. Neka za svaku funkciju \(f\) vrijedi da je \(I_n(f)\) jednako integralu njemu interpolacijskog polinoma \(p_{n,f}\) na \([a,b]\). U slučaju da je \(f \in \mathcal P_n\) vrijedi da je \(f\) sam sebi interpolacijski polinom \(p_{n,f}\) stupnja manjeg ili jednakog \(n\), pa zato vrijedi

\[I_n(f) = \int_a^b p_{n,f}(x) \ dx = \int_a^b f(x) \ dx.\]

Kako to vrijedi za sve \(f \in \mathcal P_n\), dokazali smo tvrdnju \((A)\).

Korak 3. Neka \(I_n(f)\) ima polinomijalni stupanj egzaktnosti barem \(n\). Posebno, egzaktna je na polinomima Lagrangeove baze \(\ell_0,\dots,\ell_n\). Za svaki takav polinom vrijedi

\[ \int_a^b \ell_k(x) \ dx = I_n(\ell_k) = \sum_{i = 0}^{n} w_i \ell_k (x_i) = w_k,\]

(budući da je \(\ell_k(x_i) = \delta_{k,i}\)), što dokazuje tvrdnju \((C)\).

Dakle, formula srednje točke, trapezna formula i Simpsonova formula imaju stupanj egzaktnosti barem \(0,1,2\), redom. No, dvije od tih formula imaju i veći stupanj egzaktnosti.

Formula srednje točke egzaktna je na polinomima stupnja \(0\), odnosno na konstantama. Drugim riječima, egzaktna je na vektorskom prostoru \([\{1\}]\). Pokušajmo tom formulom odrediti integral za funkciju \(f(x)=x\). S jedne strane imamo

\[\int_a^b f(x) dx = \int_a^b x dx = \left( \frac{x^2}{2} \right)\Bigg|_{a}^b = \frac{b^2-a^2}{2}. \]

S druge strane imamo

\[I_0 (f) = h f\left( \frac{a+b}{2}\right) = (b-a) \frac{a+b}{2} = \frac{b^2-a^2}{2}.\]

Dakle, formula je egzaktna i za funkciju \(f(x)=x\). Po linearnosti (i integral i svaka integracijska formula su linearni funkcionali), zaključujemo da je formula egzaktna na vektorskom prostoru \([\{1,x\}] = \mathcal P_1\). Direktnim računom može se vidjeti da polinome drugog stupnja ova formula ne integrira egzaktno. Zaključujemo da formula srednje točke ima stupanj egzaktnosti \(1\), iako je nastala egzaktnim integriranjem polinoma stupnja \(0\).

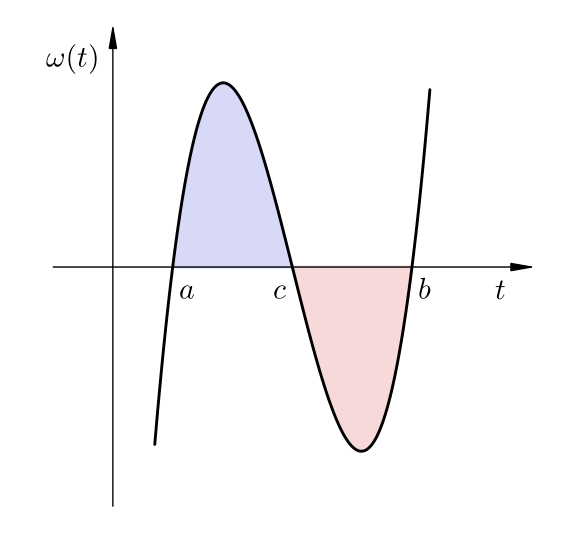
Simpsonova formula iz svoje konstrukcije egzaktna je na prostoru \(\mathcal P_2 = [\{1,x,x^2\}]\). Pogledajmo dodatno što vrijedi za polinom čvorova \(x_0 = a,x_1=\dfrac{a+b}{2},x_2=b\):

\[\omega(x)=(x-a)\left(x-\dfrac{a+b}{2}\right)(x-b).\]

U točkama \(x_0\), \(x_1\) i \(x_2\) polinom \(\omega\) jednak je nuli, pa je \(I_2(\omega) = 0\). S druge strane, direktnim računom, ili uočavanjem da je graf funkcije \(\omega\) centralno simetričan u odnosu na polovište \(c:=\dfrac{a+b}{2}\) vidimo da je i točna vrijednost integrala funkcije \(\omega\) na \([a,b]\) jednaka nuli. Dakle, Simpsonova formula egzaktna je i za funkciju \(\omega\), pa je po linearnosti egzaktna na \([\{1,x,x^2,\omega(x)\}]\). Funkcija \(\omega(x)\) polinom je trećeg stupnja, linearno je nezavisna s polinomima stupnja manjeg od \(3\), pa zajedno s \(1, x, x^2\) čini bazu za \(\mathcal P_3\). Dakle, Simpsonova formula ima stupanj egzaktnosti jednak \(3\) (ponovno se može provjeriti da ni za koji polinom četvrtog stupnja Simpsonova formula ne daje točnu vrijednost integrala).

Analogno se može pokazati da svaka Newton-Cotesova formula za \(n=2k\) ima stupanj egzaktnosti \(2k+1\).

Napomena

Spomenimo da formula srednje točke strogo formalno ne priprada familiji (zatvorenih) Newton-Cotesovih formula budući da ne postoji ekvidistantna mreža od jedne točke koja uključuje oba ruba \(a\) i \(b\), no prirodno ju je spomenuti pored trapezne i Simpsonove budući da je stvorena tako da je egzaktna na polinomima stupanja \(P_0\), na simetričnoj mreži od jedne točke na intervalu \([a,b]\).

Ocjene grešaka Newton-Cotesovih formula#

Kako podintegralnu funkciju \(f\) u integralnim formulama mijenjamo odgovarajućim interpolacijskim polinomom, ocjene za greške integralnih formula bit će izvedene ocjenama interpolacijskih polinoma, za što ćemo koristiti Teorem 3.10 ili Teorem 3.12. Nadalje, kako samo trapezna formula ima isti stupanj egzaktnosti kao i stupanj interpolacijskog polinoma kojim je izvedena, rezultate ocjene greške bit će najjednostavniji u tom slučaju.

Rezultat o formuli srednje točke bit će poseban slučaj rezultata za Gauss-Legendrove formule, pa ćemo ga dokazati kasnije. Ovdje ga radi potpunosti navodimo bez dokaza.

Teorem 5.13 (Ocjena greške formule srednje točke)

Neka je dana funkcija \(f \in C^2([a,b])\). Tada je ocjena greške formule srednje točke dana s

(5.3)#\[ \left| \int_a^b f(x)dx - I_0(f) \right| \leq \frac{(b-a)^3}{24} M_2,\]

gdje je \(M_{n} := \max_{x \in [a, b]} |f^{(n)}(x)|\).

Dokažimo sada rezultat za trapeznu formulu. Primijetimo sličnost ocjene s prethodnim rezultatom.

Teorem 5.14 (Ocjena greške trapezne formule)

Neka je dana funkcija \(f \in C^2([a,b])\). Tada je ocjena greške trapezne formule dana s

(5.4)#\[ \left| \int_a^b f(x)dx - I_1(f) \right| \leq \frac{(b-a)^3}{12} M_2.\]

Dokaz.

Neka je \(p_1\) interpolacijski polinom za funkciju \(f\) u točkama \(x_0=a\), \(x_1 = b\). Za svaku točku \(x \in \langle a,b\rangle\) primijenimo Teorem 3.10: postoji točka \(\xi_x\) koja može ovisiti o \(x\) takva da je

(5.5)#\[\left| f(x) - p_1(x) \right| = \left| \frac{\omega(x)}{2!} f''(\xi_x) \right| \leq \frac{1}{2} M_2 |\omega(x)|.\]

Tada ocjenjujemo:

\[\begin{split}\begin{align*} \left| \int_a^b f(x)dx - I_1(f) \right| &= \left| \int_a^b f(x)dx - \int_a^b p_1(x)dx \right| \\ &\leq \int_a^b \left| f(x) - p_1(x) \right|dx \\ &\leq \frac{1}{2} M_2 \int^a_b |\omega(x)| dx, \end{align*}\end{split}\]

gdje smo redom smo koristili da je trapezna formula izvedena tako da bude egzaktna na interpolacijskom polinomu prvog stupnja, pa nejednakost trokuta za integrale, te (5.5). Na kraju, kako je \(\omega (x) = (x-a)(x-b)\), vrijedi

\[\begin{split}\begin{align*} \int_a^b |\omega (x)| dx &= \int_a^b (x-a)(b-x)dx \\ &= \int_a^b (-x^2 +x (a+b) - ab) dx\\ &= \frac{a^3-b^3}{3} + \frac{b^2-a^2}{2} (a+b) - ab(b-a) \\ &= \frac{1}{6} (b-a)^3, \end{align*}\end{split}\]

odakle slijedi tvrdnja.

Dokažimo sada rezultat za Simpsonovu formulu. Ako primijenimo isti princip dokaza kao u gornjem rezultatu, dobili bismo ocjenu reda \(\mathcal O(h^4)\). No, ocjena može biti bolja.

Teorem 5.15 (Ocjena greške Simpsonove formule)

Neka je dana funkcija \(f \in C^4([a,b])\). Tada je ocjena greške Simpsonove formule dana s

(5.6)#\[ \left| \int_a^b f(x)dx - I_2(f) \right| \leq \frac{(b-a)^5}{2880} M_4.\]

Kako je dobivena ocjena bolja, i princip dokazivanja mora biti delikatniji. Ako promotrimo ponovno dokaz Teorema 5.14, član u ocjeni \((b-a)^3\) došao je integriranjem apsolutne vrijednosti funkcije \(\omega(x)\), koji je drugog stupnja, dok se član \(M_2\) pojavio zbog člana \(f''(\xi)\) iz ocjene interpolacijskog polinoma. Kako bismo za Simpsonovu formulu dobili ocjenu koja je boljeg oblika od \(C (b-a)^4 M_3\), moramo iskoristiti neki trik kako bismo \(\omega(x)\) pretvorili u neki polinom još višeg stupnja, te još jednom derivirati funkciju \(f\).

Dokaz.

Neka je \(p_2\) interpolacijski polinom za funkciju \(f\) u točkama \(x_0=a\), \(x_1 = \dfrac{a+b}{2}\), \(x_2 = b\). Za svaku točku \(x \in \langle a,b\rangle\) primijenimo Teorem 3.12:

\[f(x) - p_2(x) = \omega(x) f[x_0,x_1,x_2,x],\]

odakle integriranjem dobivamo

\[\int_a^b f(x) - p_2(x) dx = \int_a^b \omega(x) f[x_0,x_1,x_2,x] dx.\]

Cilj nam je na umnožak pod integralom s desne strane primijeniti parcijalnu integraciju. Derivaciju izraza \(f[x_0,x_1,x_2,x]\) znamo prema Propoziciji 3.15. Za \(\omega(x)\) nam je potrebna primitivna funkcija. Za svaki \(x\in [a,b]\) definirajmo

\[W(x) := \int_a^x \omega(t) dt.\]

Funkcija \(W\) primitivna je funkcija od \(\omega\) (vrijedi \(W'(x)=\omega(x))\), očito je \(W(a)=0\), a zbog \(\int_a^b \omega(x)dx = 0\) vrijedi i \(W(b) = 0\). Sada parcijalnom integracijom imamo

\[\begin{split}\begin{align*} \int_a^b f(x) - p_2(x) dx &= \int_a^b \omega(x) f[x_0,x_1,x_2,x] dx\\ &= \int_a^b W'(x) f[x_0,x_1,x_2,x] dx\\ &= -\int_a^b W(x) \frac{d}{dx} f[x_0,x_1,x_2,x] dx + \left( W(x) f[x_0,x_1,x_2,x] \right)\Big|_a^b\\ &= - \int_a^b W(x) f[x_0,x_1,x_2,x,x] dx. \end{align*}\end{split}\]

Konačno, zbog Propozicije 3.13 imamo \(f[x_0, x_1, x_2, x, x] = \frac{f^{(4)}(\xi_x)}{4!}\) za neki \(\xi_x \in [a, b]\), tj. \(|f[x_0, x_1, x_2, x, x]| \leq \frac{M_4}{24}\), pa je

\[\left| \int_a^b f(x) - p_2(x) dx \right| = \left| \int_a^b W(x) f[x_0,x_1,x_2,x,x] dx \right| \leq \frac{1}{24} M_4 \int_a^b |W(x)| dx.\]

Preostalo je izračunati \(\int_a^b |W(x)| dx\), za što još treba prije izračunati \(W(x)\).

Prvo tvrdimo da vrijedi

\[W(x) = \frac{1}{4} (x-a)^2(x-b)^2.\]

Kako postoji točno jedna primitivna funkcija funkcije \(\omega(x)\) za koju je \(W(a)= 0\), dovoljno je samo provjeriti da derivacija gornje funkcije daje \(\omega(x)\):

\[\begin{split}\begin{align*} \left( \frac{1}{4} (x-a)^2(x-b)^2 \right)' &= \frac{1}{4} \left[ 2(x-a)(x-b)^2 + (x-a)^2 2(x-b) \right] \\ &= \frac{1}{2} (x-a) (x-b) \left[ (x-b) + (x-a) \right] \\ &= (x-a)(x-b) \left(x-\frac{a+b}{2}\right) = \omega(x). \end{align*}\end{split}\]

Posebno, funkcija \(W(x)\) je nenegativna, pa je \(|W(x)| = W(x)\). Definirajmo \(h:=b-a\) i bez smanjenjenja općenitosti pretpostavimo da je \(a=0\), \(b=h\) (inače za integral možemo primijeniti zamjenu varijabli \(x \mapsto x-a\)). Konačno imamo

\[\begin{split}\begin{align*} \int_a^b |W(x)| dx &= \frac{1}{4} \int_0^h x^2 (x-h)^2 dx \\ &= \frac{1}{4} \int_0^h (x^4 - 2hx^3 + h^2 x^2 ) dx \\ &= \frac{1}{4} \left( \frac{h^5}{5} - 2h\frac{h^4}{4} + h^2 \frac{h^3}{3} \right)\\ &= \frac{1}{4} \frac{h^5}{30}. \end{align*}\end{split}\]

Kako je \(24 \cdot 4 \cdot 30 = 2880\), slijedi tvrdnja.

Produljene integracijske formule#

Pogledajmo implementaciju Newton-Cotesovih formula proizvoljnog reda u Pythonu. Aproksimiramo integral \(\displaystyle \int_{-1}^1 \frac{dx}{1+x^2}\) varirajući red \(n\) u formuli.

Integrali pomocu Newton-Cotesovih formula
  n   	   I_n(f)    	   greska
----- 	 ----------- 	 -----------
 1.00000e+00 	 5.70796e-01
 1.66667e+00 	 9.58703e-02
 1.60000e+00 	 2.92037e-02
 1.56000e+00 	 1.07963e-02
 1.56561e+00 	 5.18547e-03
 1.57304e+00 	 2.24397e-03
 1.57199e+00 	 1.19000e-03
 1.57023e+00 	 5.65888e-04
 1.57048e+00 	 3.15369e-04
 1.57096e+00 	 1.59035e-04

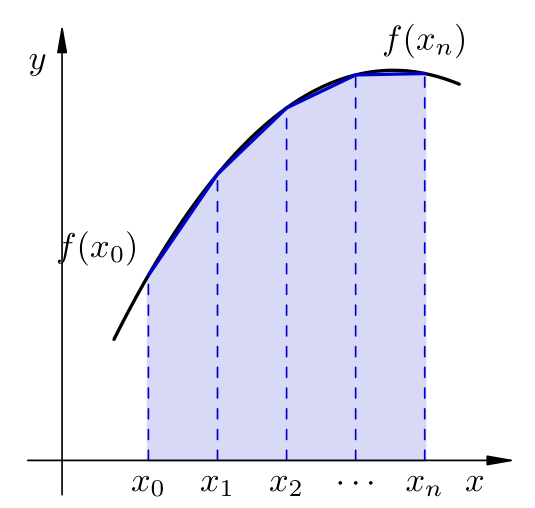
Kako bismo popravili točnost integracijskih formula, možemo povećavati \(n\) i tražiti integracijske formule koje će biti egzaktne na sve većim prostorima \(\mathcal P_n\) i za koje očekujemo sve bolju ocjenu pogreške. Drugi način, koji se u poglavlju interpolacije polinomom pokazao korisnim, je da domenu \([a,b]\) razbijemo na manje dijelove i na svakom od njih primijenimo neku od gornjih integracijskih formula (relativno niskog reda). Drugi način se u praksi pokazuje kao bolji put.

Dakle, ako su u nekom intervalu \([a,b]\) odabrane točke \(a=x_0 < x_1 < \dots < x_m = b\), integral proizvoljne funkcije na \([a,b]\) možemo aproksimirati formulom

\[\int_a^b f(x) \ dx = \sum_{i=1}^m \int_{x_{i-1}}^{x_i} f(x) \ dx \approx \sum_{i=1}^m I^{[x_{i-1},x_i]} (f) = \sum_{i=1}^m \sum_{k=0}^{n} w_k^{[x_{i-1},x_i]} f(y_k^{[x_{i-1},x_i]}),\]

gdje je

\[I^{[a,b]} (f) = \sum_{k=0}^{n} w_k^{[a,b]} f(y_k^{[a,b]})\]

neka (ne nužno Newton-Cotesova) integracijska formula na proizvoljnom intervalu \([a,b]\).

Napomena

Primijetite da težine i čvorovi moraju ovisiti o intervalu na kojem računamo integral. Međutim, tu vezu možemo izraziti eksplicitno. Označimo s \(w_k:=w_k^{[-1,1]}\) i \(y_k:=y_k^{[-1,1]}\) težine i čvorove integracijske formule \(I^{[a,b]} (f)\) na intervalu \([-1,1]\). Za račun na proizvoljnom intervalu \([a,b]\) potrebno je izvesti zamjenu varijabli funkcijom \(\varphi(y) = \frac{b-a}{2}y+\frac{b+a}{2}\). Ta funkcija bijektivno preslikava \([-1, 1]\) na \([a, b]\). Slijedi

\[\begin{split}\begin{align*} \int_a^b f(x) \ dx &= \begin{bmatrix} x = \varphi(y) = \frac{b-a}{2}y+\frac{b+a}{2} \\ dx = \varphi'(y) dy = \frac{b-a}{2} y \end{bmatrix} = \frac{b-a}{2} \int_{-1}^1 f(\varphi(y)) \ dy \\ & \approx \frac{b-a}{2} I^{[-1,1]} (f\circ \varphi) = \frac{b-a}{2} \sum_{k=0}^{m} w_k f(\varphi(y_k)) \\ &= \sum_{k=0}^{m} \frac{b-a}{2} w_k f\bigg(\frac{b-a}{2}y_k+\frac{b+a}{2}\bigg), \end{align*}\end{split}\]

odakle čitamo da je

\[w_k^{[a,b]} = \frac{b-a}{2}w_k^{[-1,1]} , \quad y_k^{[a,b]} = \frac{b-a}{2}y_k^{[-1,1]}+\frac{b+a}{2}.\]

Primijenimo ovu ideju na trapeznu i Simpsonovu integracijsku formulu. Radi jednostavnosti, pretpostavljamo da su točke \(x_i\) ekvidistantne: za sve \(i=1,\dots,n\) vrijedi \(x_{i}-x_{i-1} = h :=\frac{b-a}{n}\). U slučaju trapezne formule točke \(x_i\) kojima smo podijelili interval \([a,b]\) upravo su čvorovi integracije. Zato imamo

\[\int_a^b f(x) \ dx \approx \sum_{i=1}^n I^{[x_{i-1},x_i]}_1 (f) = \sum_{i=1}^n \frac h2 \left(f(x_{i-1}) + f(x_i) \right) = \dfrac h2 f(a) + h \sum_{i=1}^{n-1} f(x_{i}) + \dfrac h2 f(b). \]

Definicija 5.16 (Produljena trapezna formula)

Za neki \(n\in \N\) i čvorove \(x_i = a + ih\), \(i=0,1,\dots,n\) (\(h = \frac{b-a}{n}\)), integracijska formula

\[\int_a^b f(x) \ dx \approx I^{PT}_n(f) := \dfrac h2 f(a) + h \sum_{i=1}^{n-1} f(x_{i}) + \dfrac h2 f(b)\]

naziva se produljena trapezna formula.

U slučaju Simpsonove formule, nakon što interval \([a,b]\) podijelimo na \(n\) jednakih dijelova, u svakom od tih manjih intervala trebamo uzeti i polovište. Zato ćemo prilagoditi oznake: neka su točke \(a=x_0<x_1<\dots <x_{2n}=b\) ekvidistantne u intervalu \([a,b]\) uz oznaku \(h = \frac{b-a}{2n}\) (dakle \(x_{i}-x_{i-1} = h\)). Simpsonovu formulu primjenjujemo na intervalima \([x_{2i-2},x_{2i}]\) duljine \(2h\):

\[\begin{split}\begin{align*} \int_a^b f(x) \ dx &\approx \sum_{i=1}^n I^{[x_{2i-2},x_{2i}]}_2 (f) = \sum_{i=1}^n \frac h3 \left(f(x_{2i-2}) + 4f\left(x_{2i-1} \right) + f(x_{2i}) \right) \\ &= \dfrac h3 f(a) + \dfrac{4h}{3} \sum_{i=1}^{n} f(x_{2i-1}) + \dfrac{2h}{3} \sum_{i=1}^{n-1} f(x_{2i}) +\dfrac h3 f(b) \end{align*}\end{split}\]

Definicija 5.17 (Produljena Simpsonova formula)

Za neki \(n\in \N\) i čvorove \(x_i = a + ih\), \(i=0,1,\dots,2n\) (\(h = \frac{b-a}{2n}\)), integracijska formula

\[\int_a^b f(x) \ dx \approx I^{PS}_n(f) := \dfrac h3 f(a) + \dfrac{4h}{3} \sum_{i=1}^{n} f(x_{2i-1}) + \dfrac{2h}{3} \sum_{i=1}^{n-1} f(x_{2i}) +\dfrac h3 f(b)\]

naziva se produljena Simpsonova formula.

Primjenom ocjena grešaka za trapeznu i Simpsonovu formulu (Teorem 5.14 i Teorem 5.15) na svakom od intervala dobivamo ocjene grešaka za izvedene produljene formule.

Teorem 5.18 (Ocjena greške produljene trapezne formule)

Neka je dana funkcija \(f \in C^2([a,b])\). Tada je ocjena greške produljene trapezne formule dana s

\[ \left| \int_a^b f(x)dx - I_n^{PT}(f) \right| \leq \frac{(b-a)^3}{12n^2} M_2.\]

Dokaz.

Koristeći redom definiciju produljene formule (zajedno s nejednakosti trokuta) i ocjenu trapezne formule na svakom od intervala \([x_{i-1},x_{i}]\) (zajedno s \(\displaystyle \max_{x \in [x_{i-1}, x_{i}]} |f''(x)| \leq \max_{x \in [a,b]} |f''(x)| = M_2\)), dobivamo

\[\begin{split}\begin{align*} \left| \int_a^b f(x)dx - I_n^{PT}(f) \right| &\leq \sum_{i=1}^n \left| \int_{x_{i-1}}^{x_i} f(x)dx - I_1^{[x_{i-1},x_{i}]}(f) \right| \\ &\leq \sum_{i=1}^n \frac{h^3}{12} M_2 = \frac{n(b-a)^3}{12n^3} M_2 = \frac{(b-a)^3}{12n^2} M_2. \end{align*} \end{split}\]

Teorem 5.19 (Ocjena greške produljene Simpsonove formule)

Neka je dana funkcija \(f \in C^4([a,b])\). Tada je ocjena greške produljene Simpsonove formule dana s

\[ \left| \int_a^b f(x)dx - I_n^{PS}(f) \right| \leq \frac{(b-a)^5}{2880n^4} M_4.\]

Dokaz.

Dokaz je analogan prošlom, uz to što moramo paziti na to da su intervali na kojima primijenjujemo Simpsonovu formulu duljine \(2h\):

\[\begin{split}\begin{align*} \left| \int_a^b f(x)dx - I_n^{PS}(f) \right| &\leq \sum_{i=1}^n \left| \int_{x_{2i-2}}^{x_{2i}} f(x)dx - I_2^{[x_{2i-2},x_{2i}]}(f) \right| \\ &\leq \sum_{i=1}^n \frac{(2h)^5}{2880} M_4 = n\frac{(b-a)^5}{2880n^5} M_4 = \frac{(b-a)^5}{2880n^4} M_4. \end{align*} \end{split}\]

Gauss-Legendrove formule#

U pristupu za izvod Newton-Cotesovih formula krenuli smo od fiksirane mreže točaka \(x_0,x_1,\dots,x_n\) u domeni \([a,b]\). Na taj način, dobili smo integracijske formule oblika

\[\int_a^b f(x) dx \approx I(f) = \sum_{i=0}^n w_i f(x_i),\]

i koje su bile polinomijalnog stupnja egzaktnosti barem \(n\), budući da smo imali \(n+1\) parametara na raspolaganju (trebalo je za to odrediti težine \(w_i\)). Postavlja se pitanje: možemo li izabrati mrežu u domeni \([a,b]\) tako da maksimiziramo polinomijalni stupanj egzaktnosti, a time i postignemo bolje ocjene pogreške?

Radi jednostavnosti to ćemo napraviti za domenu \([-1,1]\).

Primjer 5.20

Pronađimo parametre \(w_1\), \(w_2\), \(x_1\), \(x_2\) tako da integracijska formula oblika

\[\int_{-1}^1 f(x) dx \approx I(f) = w_1 f(x_1) + w_2 f(x_2)\]

bude što većeg stupnja egzaktnosti. Po definiciji stupnja egzaktnosti, integracijska formula točno računa integrale za funkcije \(1,x,\dots,x^m\), gdje je \(m\) stupanj egzaktnosti. Kako imamo \(4\) parametra na raspolaganju, za očekivati da ćemo ih moći odrediti iz četiri jednadžbe, tj. da je formula egzaktna na polinomima \(1,x,x^2,x^3\). Uvrštavanjem dobivamo

\[\begin{split}\begin{align*} 2=\int_{-1}^1 1 dx = I(1) &= w_1 +w_2\\ 0=\int_{-1}^1 x dx = I(x) &= w_1x_1 +w_2x_2\\ \frac{2}{3}=\int_{-1}^1 x^2 dx = I(x^2) &= w_1x_1^2 +w_2x_2^2\\ 0=\int_{-1}^1 x^3 dx = I(x^3) &= w_1x_1^3 +w_2x_2^3. \end{align*}\end{split}\]

Uvrštavanjem \(w_1x_1 = -w_2x_2\) iz druge jednadžbe u četvrtu, dobivamo

\[0= w_1x_1 (x_1^2 - x_2^2),\]

odakle dobivamo \(4\) slučaja: \(w_1 = 0\), \(x_1 = 0\), \(x_1 = x_2\) ili \(x_1 = -x_2\). Direktnom provjerom može se vidjeti da samo zadnji slučaj vodi ka rješenju cijelog \(4\times 4\) sustava. Tada iz druge jednadžbe \(w_1x_1+w_2x_2 = 0\) dobivamo da je \(w_1 = w_2\), što iz prve jednadžbe znači da su te težine jednake \(1\). Konačno, treća jednadžba vodi na \(\dfrac 23 = 2x_1^2\), odakle je \(x_1 = - x_2 = \dfrac{\sqrt{3}}{3}\).

U gornjem primjeru pokazali smo kako oslobađanjem uvjeta za vrijednosti čvorova integracije možemo dobiti veći stupanj egzaktnosti nego u slučaju Newton-Cotesovih formula. Cilj nam je to napraviti za sve \(n\in \N\), na neki način koji je elegantniji od rješavanja nelinearnog sustava jednadžbi.

Oprez: Promjena notacije!

U nastavku ćemo čvorove integracije označavati sa \(x_1,x_2,\dots,x_n\) umjesto sa \(x_0, x_1, \ldots, x_n\) kao do sada. To je običaj kod Gauss-Legendreovih formula.

Koristit ćemo i Hermiteov interpolacijski polinom, koji će zbog promijenjene notacije sada biti stupnja 2n-1 (umjesto 2n+1 kao u cjelini o Hermiteovoj interpolaciji).

To ćemo napraviti koristeći Hermiteov interpolacijski polinom, za koji smo u Teoremu 3.23 našli bazu sastavljenu od polinoma \(h_{k, 0}\) i \(h_{k, 1}\), \(k=1, \ldots, n\) takvih da vrijedi:

\[\begin{split}h_{k, 0}(x_i) = \left\{\begin{array}{ll} 0, & \text{ za } i \neq k, \\ 1, & \text{ za } i = k, \\ \end{array}\right. \quad\quad h'_{k, 0}(x_i) = 0, \text{ za sve } i,\end{split}\]

\[\begin{split}h_{k, 1}(x_i) = 0, \text{ za sve } i, \quad\quad h'_{k, 1}(x_i) = \left\{\begin{array}{ll} 0, & \text{ za } i \neq k, \\ 1, & \text{ za } i = k. \\ \end{array}\right.\end{split}\]

Koristeći tu bazu i ideju raspisa kao za Newton-Cotesove formule, integral funkcije \(f\) na intervalu \([-1,1]\) aproksimiramo integralom odgovarajućeg Hermiteovog interpolacijskog polinoma i dobivamo

\[\begin{split}\begin{align*} \int_{-1}^1 f(x) dx &\approx \int_{-1}^1 h_{2n-1}(x) dx \\ &= \int_{-1}^1 \left( \sum_{i=1}^n f(x_i) h_{i,0}(x) + \sum_{i=1}^n f'(x_i) h_{i,1}(x) \right) dx \\ &= \sum_{i=1}^n f(x_i) \int_{-1}^1 h_{i,0}(x) dx + \sum_{i=1}^n f'(x_i) \int_{-1}^1 h_{i,1}(x) dx. \end{align*}\end{split}\]

Iako postoje integracijske formule koje uključuju i derivaciju funkcije \(f\), cilj nam je naći integracijsku formulu koja ne uključuje takve čvorove. Zato u gornjoj formuli biramo one čvorove za koje će težine koje stoje uz članove \(f'(x_i)\) postati nula. Dakle, za svaki \(i\) želimo postići

\[\int_{-1}^1 h_{i,1}(x) dx = 0.\]

Tada ćemo imati integracijsku formulu oblika

(5.7)#\[\int_{-1}^1 f(x) dx \approx I(f) := \sum_{i=1}^n w_i f(x_i), \quad w_i:= \int_{-1}^1 h_{i,0}(x) dx, \quad i=1,\dots,n.\]

Kako bi težine uz \(f'(x_i)\) postale nula, koristimo definiciju polinoma \(h_{i,1}\) iz Teorema 3.23:

\[ h_{i, 1}(x) = \ell_i^2(x)(x-x_i) .\]

Korištenjem i definicije polinoma \(\ell_i(x) = \dfrac{\omega_i(x)}{\omega_i(x_i)}\) iz Lagrangeove baze, dobivamo

\[\begin{split}\begin{align*} 0 = \int_{-1}^1 h_{i,1}(x)dx &= \int_{-1}^1 (\ell_i(x))^2 (x-x_i) dx \\ &= \int_{-1}^1 \ell_i(x) \frac{\omega_i(x)}{\omega_i(x_i)} (x-x_i) dx \\ &= \frac{1}{\omega_i(x_i)} \int_{-1}^1 \ell_i(x) \omega (x) dx, \quad \text{za sve } i = 1,\dots,n. \end{align*}\end{split}\]

Koristeći činjenicu da Lagrangeovi polinomi čine bazu, uzimanjem proizvoljne linearne kombinacije uvjeta takvog oblika, dobivamo da za svaki polinom \(q \in [ \left\{ \ell_1,\dots,\ell_n \right\} ] = \mathcal P_{n-1}\) vrijedi uvjet

(5.8)#\[\langle q, \omega \rangle_{L^2} = \int_{-1}^1 q(x) \omega (x) dx = 0.\]

Da bismo postigli da integracijska formula \(I(f)\) bude stupnja egzaktnosti (barem) \(2n-1\) i ne uključuje članove s derivacijom, potrebno je pronaći čvorove mreže \(x_1,x_2,\dots,x_n\) za koje polinom čvorova \(\omega(x)\) zadovoljava gornji uvjet.

Prostor \(\mathcal P_{n}\) je \((n+1)\)-dimenzionalni vektorski prostor sa skalarnim produktom \(\langle \cdot , \cdot \rangle_{L^2} \). Uvjet (5.8) sada možemo čitati ovako: \(\omega\) je neki element iz \(\mathcal P_{n}\) koji je ortogonalan na sve elemente potprostora \(\mathcal P_{n-1}\), odnosno, \(\omega\) je element ortogonalnog komplementa \(n\)-dimenzionalnog vektorskog prostora \(\mathcal P_{n-1}\). Kako je razlika u dimenzijama prostora \(\mathcal P_{n}\) i \(\mathcal P_{n-1}\) jednaka \(1\), slijedi da polinom \(\omega\) pripada točno određenom jednodimenzionalnom prostoru. Uzimajući u obzir da je vodeći koeficijent polinoma \(\omega\) jednak \(1\), dodatno zaključujemo da je taj polinom jedinstven!

Označimo s \(P_{n}\) neki polinom iz \(\mathcal P_{n}\) koji je okomit na \(\mathcal P_{n-1}\) (neki kojem vodeći koeficijent nije nužno jednak \(1\)). Definiramo li dodatno \(P_0=1\), dokažimo indukcijom da skup \(\{ P_0,P_1, \ldots, P_n\}\) čini ortogonalnu bazu za \(\mathcal P_n\). Baza indukcije je zadovoljena trivijalno za \(n=0\), pa pretpostavimo da tvrdnja vrijedi za neki \(n\). Polinom \(P_{n+1}\) nalazi se u prostoru \(\mathcal P_{n+1}\), i dodatno, okomit je na prostor

\[[\{ P_0,P_1, \ldots, P_n\}] = \mathcal P_n.\]

Odavde čitamo da je okomit i na svaki element ortogonalne baze \(\{ P_0,P_1, \ldots, P_n\}\) (ona je ortogonalna po pretpostavci indukcije). To znači da je skup \(\{ P_0,P_1, \ldots, P_n, P_{n+1}\}\) ortogonalan \((n+2)\)-člani skup \((n+2)\)-dimenzionalnog prostora \(\mathcal P_{n+1}\), što znači da je to njegova ortogonalna baza, što je trebalo dokazati indukcijom.

Niz međusobno ortogonalnih polinoma već smo susreli u cjelini o neprekidnim najmanjim kvadratima: riječ o Legendreovim polinoma (Definicija 4.14)! Dakle, dokazali smo sljedeće: kako bismo postigli što veću polinomijalnu egzaktnost integracijske formule, polinom čvorova \(\omega\) mora (do na skalar) biti jednak \(n\)-tom Legendreovom polinomu.

Teorem 5.21 (Gauss-Legendreove integracijske formule)

Za svaki \(n \in \N\) postoji integracijska formula oblika

\[\int_{-1}^1 f(x) dx \approx I^{GL}_n(f) = \sum_{i=1}^n w_i f(x_i)\]

koja je stupnja egzaktnosti barem \(2n-1\). Čvorovi \(x_1,\dots,x_n \in \langle -1,1 \rangle\) nultočke su Legendreovog polinoma \(P_{n}\). Težine u integracijskoj formuli dane su sa

\[w_i:= \int_{-1}^1 h_{i,0}(x) dx,\]

gdje su polinomi \(h_{i,0}\) dani (za \(i=1,2,\ldots,n\))

\[\begin{split}\begin{align*} h_{i, 0}(x) &= \left( 1 - 2(x-x_i) \ell_i'(x_i) \right) \ell_i^2(x), \\ \ell_i(x) &= \frac{\omega_i(x)}{\omega_i(x_i)} = \frac{(x-x_1)(x-x_2)\cdots (x-x_{i-1})(x-x_{i+1}) \cdots (x-x_n)}{(x_i-x_1)(x_i-x_2)\cdots (x_i-x_{i-1})(x_i-x_{i+1}) \cdots (x_i-x_n)} \end{align*}\end{split}\]

(kao u Teoremu 3.23).

Težine u Gauss-Legendrovim formulama

Ranije smo u Teoremu 5.12 pokazali da integracijska formula polinomijalne egaktnosti od barem \(n-1\) mora imati težine dane formulom

\[ w_i = \int_{-1}^1 \ell_{i}(x) dx, \quad i=1, \ldots, n. \]

Iz tog teorema slijedi da formula iz Teorema 5.21,

\[ w_i = \int_{-1}^1 h_{i,0}(x) dx, \quad i=1, \ldots, n, \]

mora dati isti rezultat jer i kod Gauss-Legendreovih integracijskih formula imamo takvu polinomijalnu egzaktnost (čak i veću: \(2n-1\))!

Dokažite i direktno da obje formule za težine daju isto: iskoristite formulu za \(h_{i, 0}(x)\) pomoću \(\ell_i(x)\) i činjenicu da smo odabrali čvorove za koje je \(\int_{-1}^1 h_{i, 1}(x) dx = 0\), te da vrijedi \(\ell_i(x_k) = \ell_i^2(x_k)\).

Jedino preostalo pitanje je ima li svaki Legendreov polinom \(n\)-tog stupnja \(n\) međusobno različitih realnih nultočaka unutar intervala \(\langle -1, 1 \rangle\). Odgovor je potvrdan.

Lema 5.22

Neka je \(P_n\) \(n\)-ti Legendreov polinom. Tada \(P_n\) ima \(n\) realnih nultočaka kratnosti \(1\) koje sve leže u intervalu \(\langle -1,1 \rangle\).

Dokaz.

Neka su \(y_1, y_2, \dots, y_k\) (\(k\leq n\)) one nultočke polinoma \(P_n\) koje leže u intervalu \(\langle -1,1 \rangle\) i koje su neparne kratnosti. Primijetimo da su to upravo one točke u kojima \(P_n\) mijenja predznak. Lema tvrdi da je \(k=n\) i da su \(y_1, \ldots, y_k\) sve nultočke polinoma \(P_n\).

Pretpostavimo suprotno, tj. \(k < n\). Definirajmo funkciju

\[q(x) := (x-y_1)\dots (x-y_k);\]

ako je \(k=0\), stavimo \(q(x) = 1\). To je polinom stupnja \(k < n\), pa je \(P_n\) ortogonalan na taj polinom (jer je ortogonalan na sve \(P_k\), \(k \leq n-1\), pa i na njihovu linearnu kombinaciju). Zato vrijedi

\[\int_{-1}^1 q(x) P_n(x) dx = 0.\]

S druge strane, polinom \(q(x)P_n(x)\) je fiksnog predznaka na \(\langle -1, 1 \rangle \). Naime, nultočke tog polinoma su ili van intervala \(\langle -1,1 \rangle\), ili su parne kratnosti. Stoga vrijedi ili \(q(x)P_n(x) \geq 0\) za sve \(x \in \langle -1, 1 \rangle\) ili \(q(x)P_n(x) \leq 0\) za sve \(x \in \langle -1, 1 \rangle\). Polinom \(q(x)P_n(x)\) ima stupanj \(n+k\) i nije nul-polinom.

Kako integral neprekidne funkcije koja ne mijenja predznak na \(\langle -1, 1 \rangle \) i koja je različita od nul-funkcije ne može biti jednak \(0\) (dokažite to!), dobili smo kontradikciju. Stoga je \(k=n\), pa \(P_n\) ima \(n\) različitih nultočki unutar \(\langle -1, 1 \rangle\) i one stoga sve moraju biti jednostruke kratnosti.

Pronađimo Gauss-Legendreove integracijske formule za \(n=1\) i \(n=2\).

Za \(n=1\), nultočka prvog Legendreovog polinoma \(P_1(x)=x\) je \(x_1=0\). Funkcija \(\ell_1\) je trivijalna, iznosi \(\ell_1(x) = 1\), pa je zato \(h_{1,0} (x) = 1\) te \(w_1=\int_{-1}^1 h_{1, 0}(x) dx = 2\). Tako dobivamo formulu

\[\int_{-1}^1 f(x) dx \approx I^{GL}_1(f) = w_1 f(x_1) = 2 f(0).\]

Primijetite da je to upravo formula srednje točke na intervalu \([-1,1]\).

Za \(n=2\), nultočke drugog Legendreovog polinoma \(P_2(x)=\frac 12 (3x^2-1)\) jednake su \(x_{1,2} = \pm \frac{\sqrt3}{3}\). Za težine možemo kao i u prošlom slučaju koristiti elemente Lagrangeove pa Hermiteove baze, ili možemo iskoristiti činjenicu da je formula

\[\int_{-1}^1 f(x) dx \approx I^{GL}_2(f) = w_1 f\left( -\dfrac{\sqrt{3}}{3} \right) + w_2 f\left( \dfrac{\sqrt{3}}{3} \right)\]

polinomijalnog stupnja egzaktnosti barem \(2\cdot 2 - 1 = 3\), što posebno znači da je egzaktna za \(f(x)=1\) i \(f(x)=x\). Zato je

\[\begin{split}\begin{align*} 2=\int_{-1}^1 1 dx = I^{GL}_1(1) &= w_1 +w_2\\ 0=\int_{-1}^1 x dx = I(x) &= -\dfrac{\sqrt{3}}{3} \cdot w_1 + \dfrac{\sqrt{3}}{3}w_2. \end{align*}\end{split}\]

Iz druge jednadžbe dobivamo \(w_1 = w_2\), što uvrštavanjem u prvu daje \(w_1=w_2 = 1\). Primijetite da je to upravo integracijska formula izvedena u Primjeru 5.20. Spomenimo još da za \(n=3\) se dobije integracijska formula s konstantama

\[x_1 = -\sqrt{\frac{3}{5}}, x_2 = 0, x_3 = \sqrt{\frac{3}{5}}, w_1=w_3 = \frac{5}{9}, w_2 = \frac{8}{9}.\]

Izvedimo ocjene pogreške ovih integracijskih formula.

Teorem 5.23 (Ocjena greške Gauss-Legendreovih formula)

Neka je dan \(n \in \mathbb N\) i funkcija \(f \in C^{2n}([-1,1])\). Tada je ocjena greške Gauss-Legendreove formule dana s

(5.9)#\[ \left| \int_{-1}^1 f(x)dx - I^{GL}_n(f) \right| \leq \frac{2^{2n+1}(n!)^4}{(2n+1)[(2n)!]^3} M_{2n}.\]

Dokaz.

Neka je \(h_{2n-1}\) Hermiteov interpolacijski polinom za funkciju \(f\) u točkama \(x_1,x_2,\dots,x_n\). Za svaku točku \(x \in \langle -1,1\rangle\) primijenimo Teorem 3.24: postoji točka \(\xi_x\) koja može ovisiti o \(x\) takva da je

\[\left| f(x) - h_{2n-1}(x) \right| = \left| \frac{\omega(x)^2}{(2n)!} f^{(2n)}(\xi_x) \right| \leq \frac{1}{(2n)!} M_{2n} \omega(x)^2.\]

To koristimo u ocjeni kao i prije, pa dobivamo

\[ \left| \int_{-1}^1 f(x)dx - I^{GL}_n(f) \right| \leq \frac{1}{(2n)!} M_{2n} \int_{-1}^1 \omega(x)^2 dx.\]

Preostalo je odrediti zadnji integral. U slučaju Gauss-Legendreove integracijske formule, \(\omega(x)\) upravo je jednak \(n\)-tom normiranom Legendreovom polinomu \(P_{n}\). Ako s \(A_n\) definiramo vodeći koeficijent polinoma \(P_n\), slijedi

\[\int_{-1}^1 \omega(x)^2 dx = \int_{-1}^1 \frac{P_{n}(x)^2}{A_{n}^2} dx.\]

Iz Teorema 4.15 dobivamo da je \(\displaystyle \int_{-1}^1 P_{n}(x)^2 dx = \frac{2}{2n+1}\). Dodatno, iz Definicije 4.14 možemo pokazati da vodeći koeficijenti Legendreovih polinoma zadovoljavaju rekurziju \(A_{n+1} = \dfrac{2n+1}{n+1}A_n\), \(A_0=A_1=1\), odakle (indukcijom ili teleskopiranjem) dokazujemo

\[A_{n} = \frac{(2n-1)!!}{n!} = \frac{(2n)!}{(2n)!! \cdot n!} = \frac{(2n)!}{2^{n} \cdot (n!)^2}\]

(\(m!!\) označava umnožak svih prirodnih brojeva manjih ili jednakih \(m\) iste parnosti kao \(m\); koristimo da je \(m!! \cdot (m+1)!!\) umnožak svih prirodnih brojeva manjih ili jednakih \(m+1\), te kada u izrazu \((2m)!!\) izlučimo \(2\) iz svakog faktora preostaje nam \(m!\)). Množenjem dobivenih konstanti dokazujemo tvrdnju.

Za općeniti \(n\) koristili smo tvrdnju \(\displaystyle \int_{-1}^1 P_{n}(x)^2 dx = \frac{2}{2n+1}\) koju nismo dokazali. Međutim, \(n=1\), tu tvrdnju je jednostavno za provjeriti jer uistinu vrijedi

\[\displaystyle \int_{-1}^1 P_{1}(x)^2 dx = \int_{-1}^1 x^2 dx = \frac{2}{3},\]

pa smo time u potpunosti dokazali ocjenu pogreške za formulu srednje točke (Teorem 5.13) na \([-1,1]\).

Ovime smo razvili teoriju Gauss-Legendreovih formula na intervalu \([-1,1]\). Za proizvoljan interval \([a,b]\) potrebno je napraviti transformaciju kao što smo opisali ranije. Nadalje, kako bismo efektivno koristili Gauss-Legendreovu integraciju i dodatno smanjili grešku, u praksi ponovno koristimo produljene verzije ovih formula. Za vježbu ostavljamo da se sami uvjerite u sljedeći rezultat.

Teorem 5.24 (Produljene Gauss-Legendreove formule)

Neka su dani \(n,m\in \mathbb N\), te neka su \(w_1,\dots,w_n\) i \(x_1,\dots,x_n\) težine i čvorovi Gauss-Legendreove integracijske formule \(I^{GL}_n(f)\) na intervalu \([-1,1]\). Za funkciju \(f:[a,b] \to \R\) promatramo produljenu Gauss-Legendreovu integracijsku formulu primijenjenu na svaki od \(m\) podintervala intervala \([a,b]\) duljine \(h=\frac{b-a}{m}\):

\[I^{PGL}_{m,n} (f) = \sum_{i=1}^m \sum_{k=1}^{n} \frac{h}{2} w_k f\left(\frac{h}{2} x_k + a + \frac{2i-1}{2}h \right).\]

Ako je \(f \in C^{2n}([a,b])\), tada je zadovoljena ocjena

\[ \left| \int_{a}^b f(x)dx - I^{PGL}_{m,n}(f) \right| \leq \frac{(n!)^4}{(2n+1)[(2n)!]^3} \frac{(b-a)^{2n+1}}{m^{2n}} M_{2n}.\]

Kada \(m\to \infty\) (uz fiksan \(n\)), dobivamo \(\displaystyle I^{PGL}_{m,n}(f) \to \int_{a}^b f(x)dx \).

Primijetite da u slučaju \(m=1\) dobivamo rezultat za pomaknutu neproduljenu Gauss-Legendreovu formulu.

Pokazujemo kod u Pythonu kojim računamo \(\displaystyle \int_{-1}^1 \frac{dx}{1+x^2}\) Gauss-Legendreovim formulama sve višeg reda (bez podjele).

Integrali pomocu Gauss-Legendreovih formula
  n   	    I_n(f)   	   greska
----- 	 ----------- 	 -----------
0 	 2.00000e+00 	 4.29204e-01
1 	 1.50000e+00 	 7.07963e-02
2 	 1.58333e+00 	 1.25370e-02
3 	 1.56863e+00 	 2.16888e-03
4 	 1.57117e+00 	 3.74844e-04
5 	 1.57073e+00 	 6.46195e-05
6 	 1.57081e+00 	 1.11266e-05
7 	 1.57079e+00 	 1.91425e-06
8 	 1.57080e+00 	 3.29145e-07
9 	 1.57080e+00 	 5.65716e-08

Integral pomocu funkcije quad: 1.57080e+00.
Ocjena greske: 1.74393e-14.
Prava greska: 2.22045e-16.

Napomena

Promjenom težinske funkcije pod integralom (tj. u slučaju da tražimo aproksimaciju integrala funkcije \(\int_a^b f(x)w(x) \ dx\) za neku drugu nenegativnu funkciju \(w\)), ovisno o toj težinskoj funkciji teorija će nam dati neki drugi niz ortogonalnih polinoma, a time i drugu familiju podintegralnih funkcija. Recimo, za težinsku funkciju \(w(x)=(1-x^2)^{-1/2}\) na \([-1,1]\) dobivamo niz Čebiševljevih polinoma prve vrste, pa zato pričamo o Gauss-Čebiševljevim integracijskim formulama. Teorija ortogonalnih polinoma dakle ima utjecaja i na numeričku integraciju.