Primjer jednog problema iz primijenjene matematike#
U ovoj cjelini ćemo opisati jedan tipični problem iz primijenjene matematike i postupak njegovog rješavanja. Metoda konačnih elemenata koju ćemo pri tome izvesti je posebno prikladna u ovom trenutku jer ilustrira cijeli niz tema kojima ćemo se baviti na kolegiju Numerička matematika. Ovdje nam nije prvenstveni cilj proučavati tu metodu koja služi za nalaženje približnog rješenja diferencijalnih jednadžbi, nego ju iskoristiti samo kako bismo motivirali proučavanje drugih tema na ovom kolegiju.
Opis problema#
Elastično uže, poput onog za sušenje rublja, fiksirano je s obje strane na zid. Na uže su obješeni tereti poznate mase. Potrebno je odrediti progib (otklon od horizontale) užeta u svakoj točki.
Matematički model#
Prije rješavanja, problem je prvo potrebno formulirati jezikom matematike, tj. napraviti matematički model.
Uvedimo koordinatni sustav u kojem je \(0\) označava lijevi, a \(1\) desni zid.
Sa \(f(x)\) označimo poznatu gustoću sile kojom djelujemo na uže u točki \(x \in [0, 1]\) u \(y\)-smjeru. Ukupna sila na uže je \(\displaystyle \int_0^1 f(x)dx\).
Sa \(u(x)\) označimo okomiti progib užeta u točki \(x\). Implicitno pretpostavljamo da se točka na užetu \((x,0)\) deformirala u točku \((x,u(x))\), što možemo ako pretpostavimo da je deformacija „dovoljno mala” da takvo pojednostavljenje ne dovodi do velike greške u modelu.
Uže ima poznatu elastičnost koju ovdje opisujemo koeficijentom \(a > 0\).
Za zadanu funkciju \(f\), potrebno je odrediti funkciju \(u\).
Napomena
Dolje dokazani račun nije dokaz, već samo motivacija za model koji ćemo koristiti na kraju.
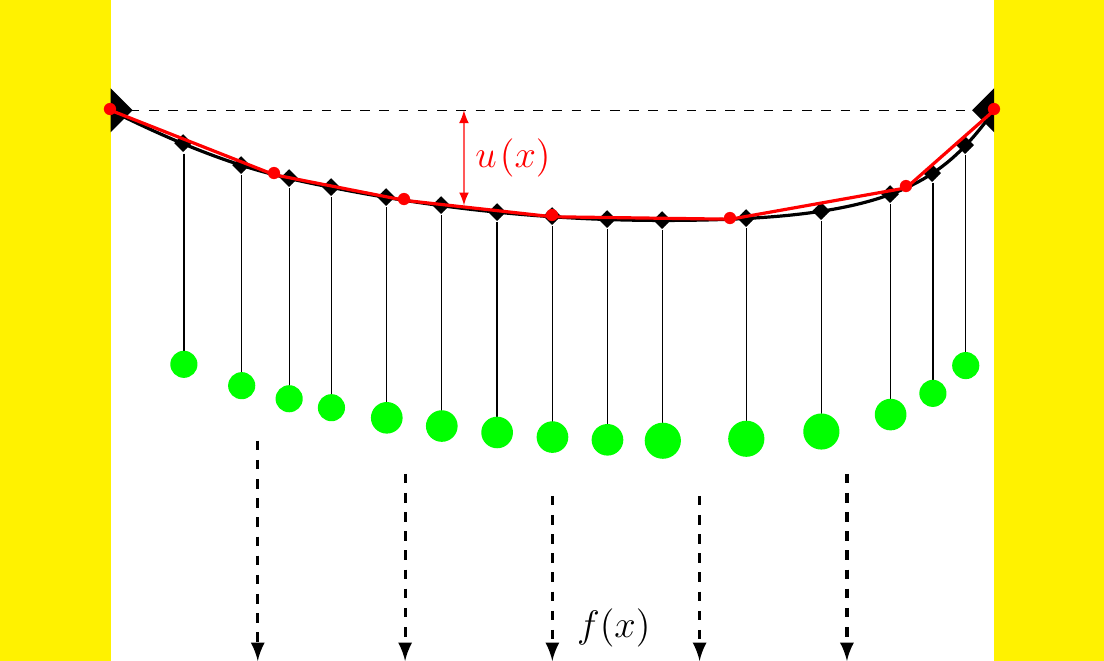
Promotrimo deformirano uže. Zamislimo da je uže zapravo sastavljeno od mnogo čvrstih valjaka visine \(h\). Promotrimo onaj kojem je centar mase u \((x,u(x))\), za neki fiksan \(x\in [0,1]\). Na njega djeluju tri sile: sila određena gustoćom \(f(x)\) i dvije sile napetosti za svaki od susjednih valjaka.
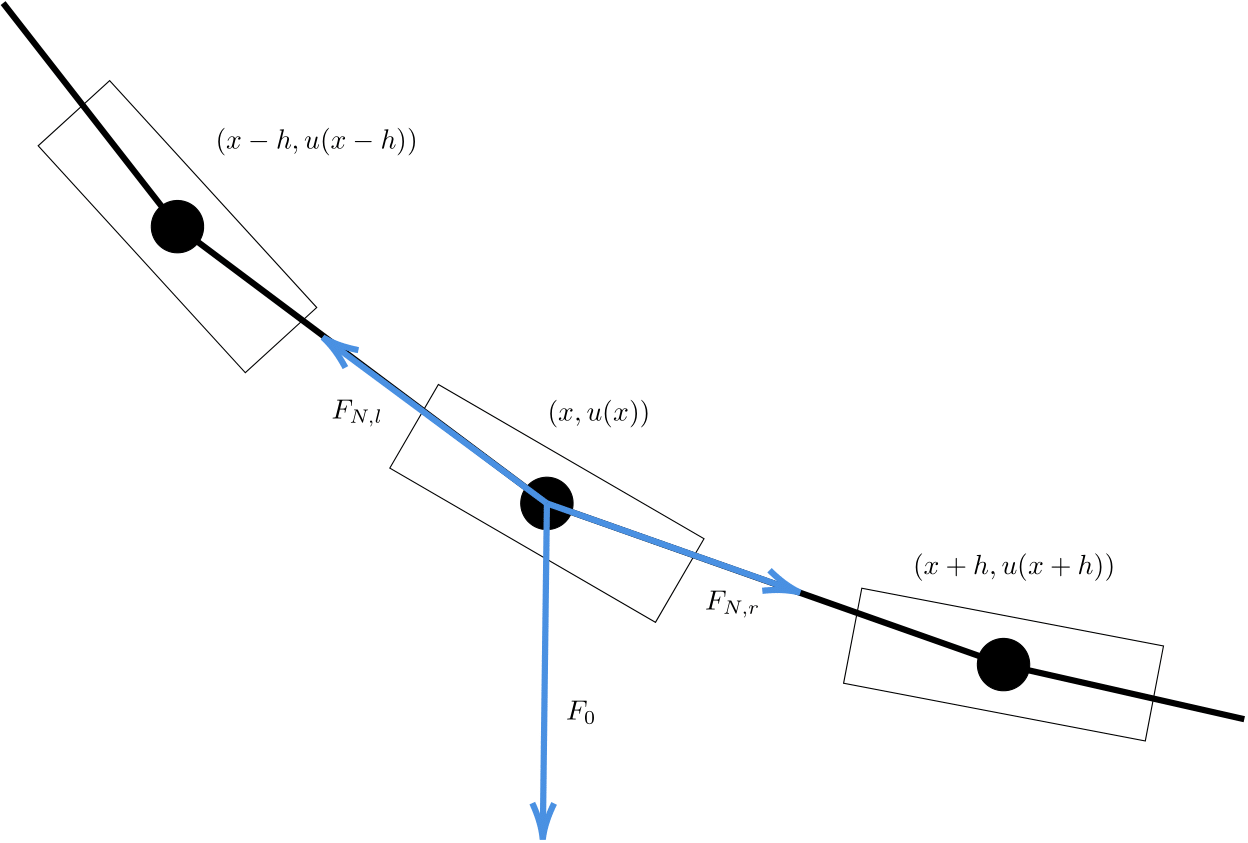
Što se tiče prve sile, kako gustoća sile \(f(x)\) djeluje na valjak visine \(h\), ukupna sila je opisana vektorom \(F_0 = (0,hf(x))\). (Zapravo, dana je integralom na intervalu opisanom tim valjkom, ali takav član čini daljnji račun ružnijim, no ne i mnogo točnijim.) Za sile napetosti znamo da djeluju u smjeru spoja dva susjedna pravokutnika. Pretpostavimo da je njihov iznos proporcionalan udaljenosti središta tih valjaka: što su ti valjci udaljeniji, to je sila veća. Za koeficijent te proporcionalnosti možemo očekivati da je baš koeficijent elastičnosti \(a>0\). Dakle, te dvije sile napetosti opisane su vektorima
Deformirano uže je u ravnoteži pa je suma svih sila koje djeluju na promatrani valjak jednaka nula. Zanimljivo je gledati samo druge komponente sila, pa iz \(F_0 + F_{N,l} + F_{N,r} = 0\) na drugim komponentama dobivamo
Kako uže zapravo nije dano kao niz valjaka, ili kako su ti valjci „beskonačno mali”, u gornja jednakost ne vrijedi kao takva nego bi u njoj trebalo pustiti limes \(h \to 0\). To možemo napraviti samo formalno, bez pravog opravdanja. Oba razlomka \(\dfrac{u(x+h)-u(x)}{h}\) i \(\dfrac{u(x)-u(x-h)}{h}\) na limesu bi trebali ispasti da su jednaki \(u'(x)\). No, za te kvocijente ponovno uzmemo razliku i podijelimo s \(h\). To je onda na limesu jednako drugoj derivaciji funkcije \(u(x)\). Dakle, time motiviramo da se ravnotežni problem užeta modelira problemom:
Napomene:
Ako je \(f\) neprekidna na \([0, 1]\), \(a>0\) i \(u(x) \in C^2([0, 1])\), onda možemo naći egzaktno rješenje ovog problema. Problem je što bismo morali dvaput integrirati, što je za neke funkcije \(f\) teško ili čak nemoguće.
U malo složenijoj situaciji (npr. uže ima varijabilnu elastičnost \(a(x)\) i nalazi se u nekom viskoznom sredstvu koje mu pruža otpor \(b(x)\)) dobili bismo složeniju diferencijalnu jednadžbu oblika
(1)#\[ -(a(x)u'(x))' + b(x)u(x) = f(x).\]Vrlo slične jednadžbe modeliraju i druge raznovrsne fizikalne situacije, npr. (1) modelira i distribuciju topline ili koncentracije.
Jednadžbu (1) općenito ne možemo eksplicitno riješiti formulom, tj. ne postoji formula za rješavanje!
Problem se može poopćiti i u više dimenzija, čime bismo dobili parcijalnu diferencijalnu jednadžbu. Problem može biti i nestacionaran, tj. možemo promatrati kako se \(u\) mijenja kroz vrijeme.
Numeričko rješavanje jednadžbe#
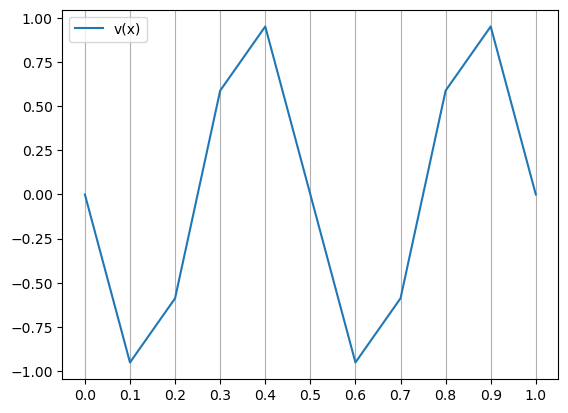
Budući da općenitu jednadžbu (1) ne možemo riješiti egzaktno, opisat ćemo postupak nalaženja približnog rješenja: tražimo \(\tilde{u} \approx u\) koji je po dijelovima linearna funkcija. Podijelimo interval \([0, 1]\) točkama \(x_0=0, x_1, \ldots, x_m, x_{m+1}=1\) na \(m+1\) jednakih intervala, te promatrajmo funkcije iz skupa
Primjer jedne takve funkcije za \(m=9\) je na donjoj slici.
Show code cell source
import numpy as np;
import matplotlib.pyplot as plt;
m = 9;
x = np.linspace( 0, 1, m+2 );
v = -np.sin( 4*np.pi*x );
plt.figure();
plt.plot( x, v, label='v(x)' );
plt.legend();
plt.xticks(x);
plt.grid( True, axis='x' );
Naišli smo na prvi problem kojim ćemo se baviti u ovom kolegiju.
Problemi aproksimacije i interpolacije
Ako je \(u \in C^2([0, 1])\), koliko dobru aproksimaciju \(\tilde{u}\) za \(u\) možemo naći koristeći se samo funkcijama iz \(\mathcal{L}\)? Drugim riječima, čak i ako nam je \(u\) poznat, kako pronaći \(\tilde{u}\) za koji se postiže
gdje je \(d\) neka mjera udaljenosti dviju funkcija, na primjer, \(d(u, \tilde{u}) = \int_0^1 (u(x) - \tilde{u}(x))^2 dx\) ili \(d(u, \tilde{u}) = \max_x |u(x) - \tilde{u}(x)|\)?
Ovo je primjer problema aproksimacije funkcije \(u\) funkcijom iz \(\mathcal{L}\). Ako tražimo \(\tilde{u} \in \mathcal{L}\) tako da vrijedi \(u(x_j) = \tilde{u}(x_j)\) za sve \(j\), onda govorimo o problemu interpolacije funkcije \(u\) funkcijom iz \(\mathcal{L}\).
Jasno, ovakva \(\tilde{u}\) neće zadovoljavati (1) jer nije ni derivabilna. Umjesto toga koristimo ideju iz linearne algebre: ako je \(U\) unitarni prostor, onda za vektor \(u \in U\) vrijedi
Skup svih neprekidnih funkcija \(v : [0, 1] \to \R\) za koje vrijedi \(v(0)=v(1)=0\) čini unitarni prostor sa skalarnim produktom
Ako pomnožimo (1) sa \(v(x)\) i integriramo, dobivamo
Parcijalnom integracijom slijedi
odnosno, zbog \(v(0)=v(1)=0\),
Ovo vrijedi za sve neprekidne funkcije \(v\) koje imaju derivaciju na \([0, 1]\) osim možda u konačno mnogo točaka. Specijalno, ovo vrijedi za sve \(v \in \mathcal{L}\). Stoga, umjesto da rješavamo (1), postavljamo skromniji cilj pronalaženja \(u \in \mathcal{L}\) takve da (2) vrijedi za sve \(v \in \mathcal{L}\). Jednadžba (2) je tzv. slaba formulacija jednadžbe (1).
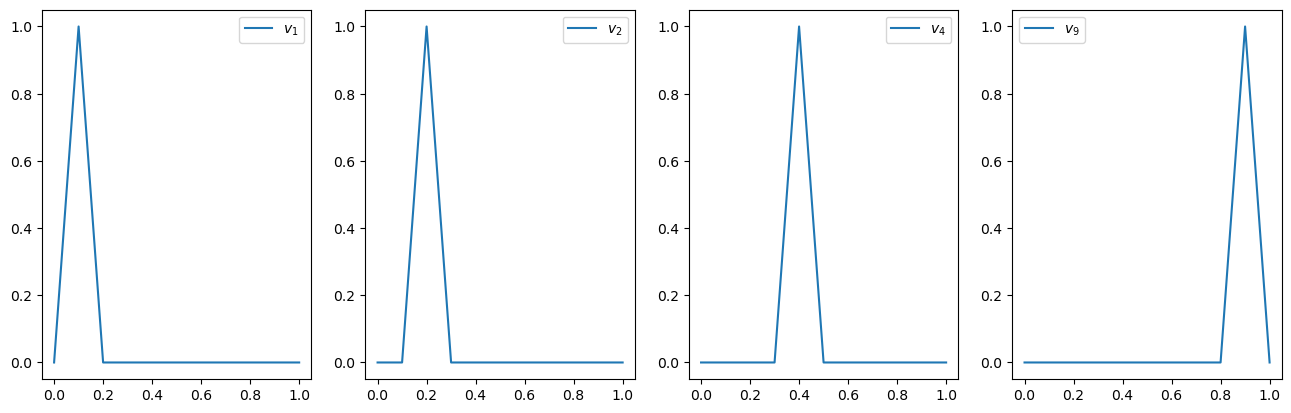
Za razliku od prostora svih neprekidnih funkcija, prostor \(\mathcal{L}\) je konačno-dimenzionalan i njegovu bazu čine funkcije \(v_1, \ldots, v_m\) prikazane na donjoj slici u slučaju \(m=9\).
Show code cell source
x = np.linspace( 0, 1, m+2 );
plt.figure(figsize=[16, 4.8]);
for (idx, i) in enumerate( [1, 2, 4, 9] ):
v = np.zeros(11);
v[i] = 1;
plt.subplot( 1, 4, idx+1 );
plt.plot( x, v, label=f'$v_{i}$' );
plt.legend();
Kako tražimo \(u \in \mathcal{L}\), potrebno je pronaći koeficijente \(\alpha_1, \ldots, \alpha_m\) u prikazu
Kao što smo rekli, (2) promatramo samo za \(v \in \mathcal{L}\). Kako je to vektorski prostor, promotriti jednadžbu (2) za sve \(v\) ekvivalentno je kao promotriti ju za elemente baze. Zato uvrštavamo \(v=v_j\):
odnosno,
Sada uočavamo sljedeći problem kojim ćemo se baviti u ovom kolegiju.
Problem numeričke integracije
Kako izračunati vrijednost određenog integrala \(\int_a^b g(x) dx\) za zadanu funkciju \(g\)?
Tehnike egzaktne integracije koje su napravljene na kolegiju Matematička analiza 2 mogu se primijeniti samo na vrlo mali broj funkcija \(g\). U praksi gotovo uvijek nailazimo na funkcije koje nije moguće egzaktno integrirati. Stoga želimo izračunati aproksimaciju određenog integrala, npr. na dovoljni broj decimala. Uz izvod metoda za približno računanje integrala, želimo dokazati i rezultate koji ograničavaju veličinu greške, tj. daju jamstvo na točnost izračunate aproksimacije.
Vratimo se natrag na jednadžbu (3). Definirajmo:
Jednadžba (3) se svodi na rješavanje linearnog sustava
Uočimo jedan detalj vezan uz bazne funkcije \(v_j\) koje imaju posljedicu na strukturu matrice \(A\):
što povlači da je matrica \(A\) simetrična i tridijagonalna:
Sa \(\xx\) smo ovdje označili da je neki element matrice različit od nule. Kada riješimo sustav \(Ax=b\), dobili smo koeficijente \(\alpha_i\) i aproksimacija za rješenje polazne diferencijalne jednadžbe je dana sa \(u(x) \approx \alpha_1 v_1(x) + \ldots + \alpha_m v_m(x)\).
Problem rješavanja linearnog sustava
Kako efikasno na računalu rješavati linearne sustave?
Na kolegijima Linearna algebra 1 i 2 ste proučavali matematičku teoriju sustava linearnih jednadžbi: uvjete egzistencije i strukturu skupa svih rješenja. Ovdje će nas zanimati efikasni algoritmi za rješavanje, a vidjet ćemo da se mogu javiti i problemi sa numeričkom stabilnosti. Izuzetno mnogo problema u praksi se na kraju svede upravo na rješavanje linearnih sustava.
Linearni sustavi koji se javljaju u praksi mogu biti izuzetno velikih dimenzija. S druge strane, tipično su te matrice rijetko popunjene – svega nekoliko elemenata u svakom retku i stupcu je različito od nule. Tako je i kod naše matrice \(A\): ona je reda \(m \times m\), ali u svakom retku ima max. 3 elementa različita od nule. Postoje brojne metode za rješavanje linearnih sustava s rijetko popunjenim matricama.
Cjelokupni postupak za rješavanje diferencijalne jednadžbe (1) s pripadnim rubnim uvjetima koji smo gore opisali se zove metoda konačnih elemenata.
Implementacija u Pythonu#
Sada smo spremni za implementaciju metode konačnih elemenata u Pythonu. Koristit ćemo \(m=100\) – unutar intervala \([0, 1]\) ćemo imati jednako razmaknute (ekvidistantne) točke \(x_0=0, x_1, \ldots, x_{100}, x_{101}=1\), a linearni sustav koji dobivamo na kraju će biti dimenzije \(100 \times 100\). Definirajmo i neku funkciju \(f(x) = -10 x \sin(2\pi x^2)^2\) kojom ćemo testirati našu metodu.
def f(x):
return -10*x * np.sin(2*np.pi*x)**2;
# Točke x0, x1, ... x_(m+1) u intervalu [0, 1].
m = 100;
x = np.linspace( 0, 1, m+2 );
# Graf funkcije f.
plt.plot( x, f(x), label='f(x)' );
plt.legend();
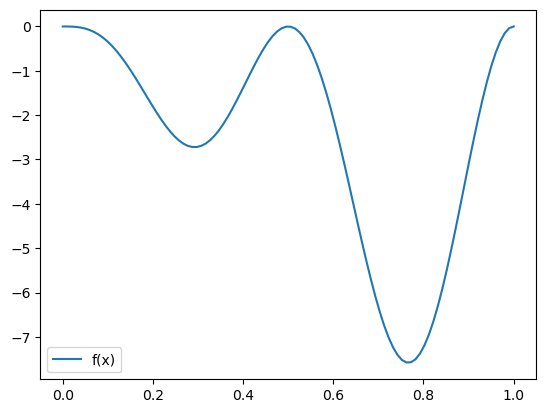
Definirajmo i funkcije \(a(x)\) i \(b(x)\) u jednadžbi (1). Uzet ćemo konstante \(a(x) = 0.05\) i \(b(x) = 0\) kao u primjeru s vješanjem rublja na uže. Probajte sami eksperimentirati s nekim drugim funkcijama!
def a(x):
return 0.05;
def b(x):
return 0;
Sada je potrebno definirati matrice \(K\) i \(L\) čiji elementi su dani sa \(K_{ij} = \int_0^1 a(x) v_i'(x) v_j'(x) dx\) i \(K_{ij} = \int_0^1 b(x) v_i(x) v_j(x) dx\) te vektor desne strane \(b\) sa \(b_j = \int_0^1 f(x) v_j(x) dx\). Prvo trebamo definirati bazne funkcije \(v_j\) i njihove derivacije.
# Bazna funkcija v_j, za j=1, 2, ..., m.
def v(j, x):
if x < (j-1)/(m+1):
# Funkcija je 0 lijevo od točke (j-1)/(m+1)...
return 0;
elif x < j/(m+1):
# ...zatim linearno raste do 1 u točki j/(m+1)...
return (x - (j-1)/(m+1)) * (m+1);
elif x < (j+1)/(m+1):
# ...pa linearno pada do 0 u točke (j+1)/(m+1)...
return ((j+1)/(m+1) - x)*(m+1);
else:
# ...i onda je 0.
return 0;
# Derivacija bazne funkcije v_j, za j=1, 2, ..., m.
def dv(j, x):
if x < (j-1)/(m+1):
# Derivacija je 0 lijevo od točke (j-1)/(m+1)...
return 0;
elif x < j/(m+1):
# ...zatim je pozitivna konstanta do točke j/(m+1)...
return (m+1);
elif x < (j+1)/(m+1):
# ...pa je negativna konstanta do točke (j+1)/(m+1)...
return -(m+1);
else:
# ...i onda je 0.
return 0;
Sada koristimo ugrađenu funkciju quad za numeričku integraciju u biblioteci scipy. Po defaultu, ta funkcija će integral aproksimirati s točnošću od \(\approx 10^{-8}\), tj. na osam decimala iza decimalne točke.
from scipy.integrate import quad;
K = np.zeros( (m, m) );
L = np.zeros( (m, m) );
bb = np.zeros( m );
for i in range( 1, m+1 ):
# Znamo da će integrali biti 0 osim za j=i-1, i, i+1.
# Sve funkcije koje integriramo će biti 0 osim na [(i-1)/(m+1), (i+1)/(m+1)].
# Zato ih integriramo samo na tom podintervalu.
donja_granica = max((i-1)/(m+1), 0);
gornja_granica = min((i+1)/(m+1), 1);
for j in range( max(i-1, 1), min(i+1, m)+1 ):
# Definiramo funkciju a(x)*v_i'(x)*v_j'(x).
fja = lambda x: a(x)*dv(i, x)*dv(j, x);
(integral, error) = quad( fja, donja_granica, gornja_granica );
K[i-1, j-1] = integral;
# Definiramo funkciju b(x)*v_i(x)*v_j(x).
fja = lambda x: b(x)*v(i, x)*v(j, x);
(integral, error) = quad( fja, donja_granica, gornja_granica );
L[i-1, j-1] = integral;
# Definiramo funkciju f(x)*v_i(x).
fja = lambda x: f(x)*v(i, x);
(integral, error) = quad( fja, donja_granica, gornja_granica );
bb[i-1] = integral;
Sada je preostalo samo riješiti linearni sustav. U Pythonu to radi funkcija solve iz biblioteke numpy.linalg.
import numpy.linalg as la;
A = K + L;
alpha = la.solve( A, bb );
# Nacrtamo konačno rješenje.
# Aproksimacija u(x) poprima točno vrijednost alpha(j) u točki x(j).
# Dodajemo još samo vrijednosti 0 u lijevom i desnom rubu.
x = np.linspace( 0, 1, m+2 );
u = np.block( [0, alpha, 0] );
plt.plot( x, f(x), label='f(x)', linestyle='dashed' );
plt.plot( x, u, label='u(x)' );
plt.legend();
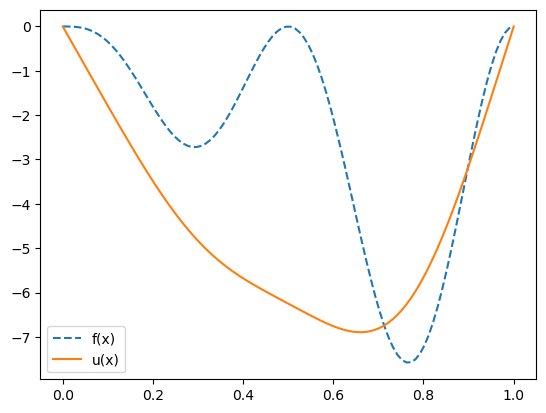
Pokušajte sami eksperimentirati s drugim izborima funkcije \(f\). Kako biste ovaj pristup poopćili na probleme u dvije dimenzije, tj. na parcijalne diferencijalne jednadžbe kojima je domena npr. jedinični kvadrat? Kako tada izgledaju problemi koje smo posebno istaknuli?
U gornjoj implementaciji smo koristili gotove funkcije poput solve i quad koje su ugrađene u biblioteku numpy. Do kraja ovog kolegija naučiti ćemo kako sami napraviti funkcije koje rješavaju probleme linearnih sustava, numeričke integracije, kao i druge probleme numeričke matematike.
Ostale teme na ovom kolegiju#
Na ovom kolegiju obradit ćemo i neke druge teme koje nismo dotaknuli u gornjim razmatranjima.
Rješavanje nelinearnih jednadžbi
Neki problemi u primjeni neće se nužno svesti na rješavanje linearnih sustava, nego, općenito, na rješavanje neke nelinearne jednadžbe ili sustav nelinearnih jednadžbi. Nelinearne jednadžbe moguće je egzaktno riješiti samo u iznimno rijetkim situacijama.
Na primjer, svi znamo formulu za rješenja jednadžbe \(ax^2+bx+c=0\); slične formule postoje i za jednadžbe trećeg i četvrtog stupnja. Međutim, može se dokazati da je nemoguće pomoću konačno mnogo primjena 4 osnovne računske operacije i vađenja proizvoljnih korijena prikazati nultočke općih jednadžbi stupnja 5 ili višeg. U srednjoj školi ste rješavali trigonometrijske i logaritamske jednadžbe poput \(\sin(x)+\cos(x)=1/2\). Sve te jednadžbe su bile namještene tako da se mogu riješiti nekom od malobrojnih metoda. Kako biste riješili, na primjer, jednadžbu \(\sin(x) + e^x = 1/2\)?
Postoje brojne tehnike kojima možemo naći aproksimativna rješenja nelinearnih jednadžbi. Na ovom kolegiju analizirat ćemo dvije metode: metodu bisekcije i Newtonovu metodu.
Optimizacija
Mnogi zadaci primijenjene matematike svode se na problem optimizacije: potrebno je pronaći minimum ili maksimum zadane funkcije \(f\) koja ovisi o nekim parametrima. Na primjer, ako na uže trebamo rasporediti \(3\) predmeta od kojih svaki ima masu od \(5\)kg, gdje ih trebamo smjestiti tako da progib užeta bude što je moguće manji?
Optimizacija može biti kontinuirana (na primjer, položaj predmeta može biti bilo gdje u intervalu \([0, 1]\)) ili diskretna (na primjer, svaki predmet mora biti smješten na nekom od ukupno 10 ponuđenih mjesta). Na ovom kolegiju bavimo se samo kontinuiranom optimizacijom: iz matematičke analize znamo da glatka funkcija \(f\) ima ekstreme u kritičnim točkama, pa se problem optimizacije tada svodi na rješavanje sustava nelinearnih jednadžbi \(\nabla f = 0\).
Treniranje neuronskih mreža nije ništa drugo nego provođenje algoritma optimizacije (na primjer, stohastičkog gradijentnog spusta) za minimizaciju neke funkcije cilja (engl. loss function) koja tipično ovisi o jako puno parametara (to su težine neuronske mreže).