1.2. Tipovi grešaka#
U ovoj cjelini ćemo detaljnije opisati nekoliko vrsta grešaka koje se događaju prilikom numeričkog rješavanja nekog problema.
Greške modela#
Pojave iz stvarnog svijeta su često previše komplicirane da bismo ih u potpunosti i savršeno točno opisali matematičkim modelom (npr. diferencijalnim jednadžbama, sustavima (ne)linearnih jednadžbi, kao probleme optimizacije, itd.). S druge strane, čak i ako imamo matematički model koji dobro opisuje fizikalnu situaciju, on može biti previše složen da bismo ga bili u stanju riješiti, pa ga moramo dodatno pojednostavniti.
Tako nastaju greške modela:
Zbog zanemarivanja utjecaja nekih sila.
Na primjer, zanemarivanje utjecaja otpora zraka ili trenja.
Zbog zamjene kompliciranog modela jednostavnijim.
Na primjer, sustavi nelinearnih običnih ili parcijalnih diferencijalnih jednadžbi se lineariziraju, da bi se dobilo barem približno rješenje.
Zbog upotrebe modela u graničnim slučajevima.
Na primjer, kod matematičkog njihala se \(\sin(x)\) aproksimira s \(x\), što vrijedi samo za male kutove.
Jedan jednostavni primjer greške modela je zanemarivanje utjecaja otpora zraka kod kosog hica.
Ako projektil ispaljujemo prema cilju:
nekom početnom brzinom \(v_0\),
pod nekim kutem \(\alpha\), obzirom na horizontalnu ravninu,
onda elementarni račun (izvedite sami, srednjoškolska fizika!) daje da će projektil pod utjecajem gravitacije doletjeti do udaljenosti
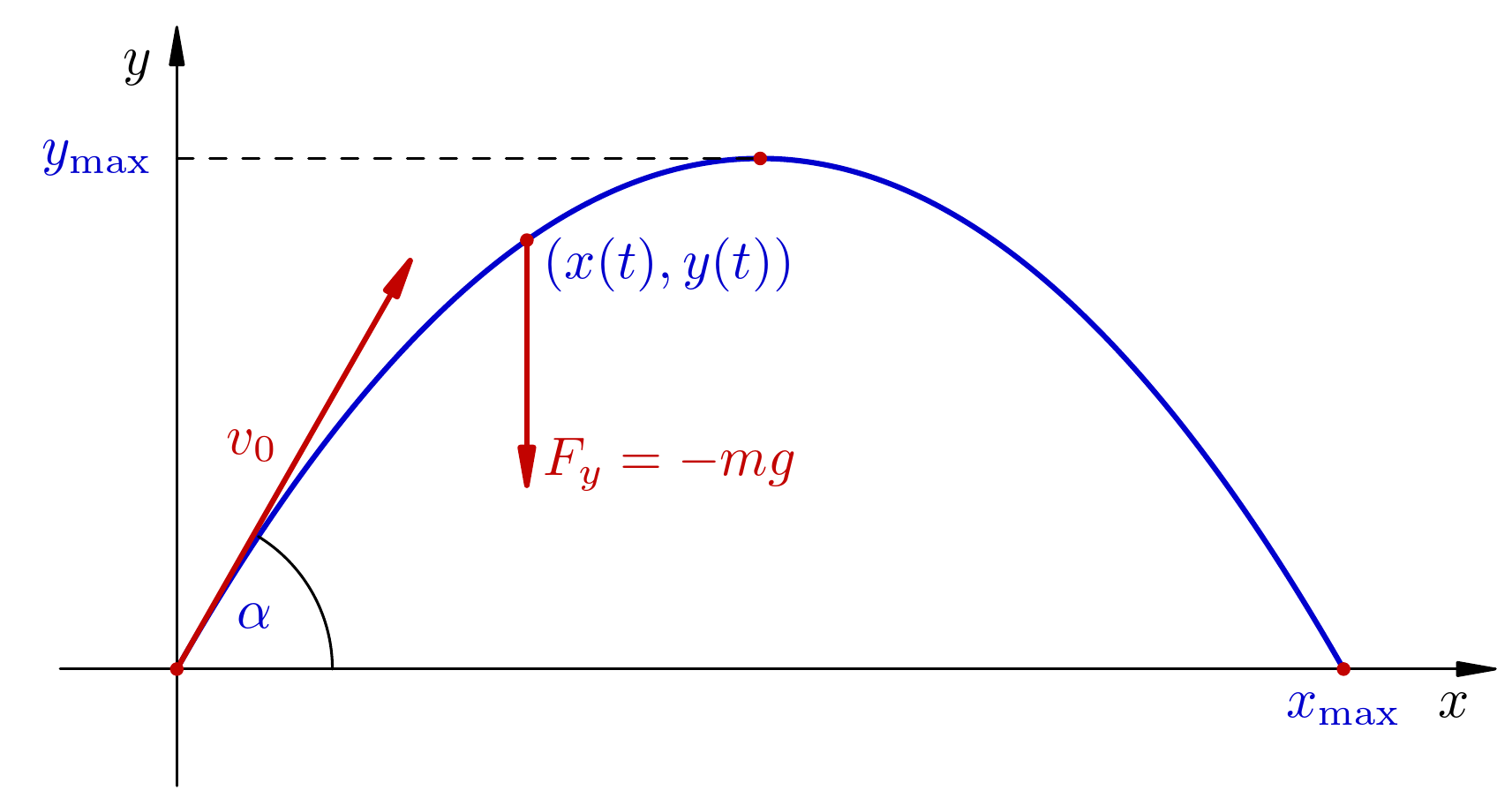
Uvrstimo li stvarne podatke za haubicu kalibra 155 mm, model H155 M65:
Početna brzina ispaljene granate je \(v_0\) = 564 m/s.
Uz gornji izračun, maksimalni domet se postiže za kut \(\alpha = 45^o = \pi/4\) i iznosi \(x_{\max} = \frac{564^2 \sin(\pi/2)}{9.81} \approx 32 425.69\) m.
Stvarni, eksperimentalno utvrđeni maksimalni domet postiže se za kut \(\alpha = 45^o 10'\) i
iznosi samo \(x_{\max} = 14 854\) m.
Ovako dramatična razlika nastala je zbog zanemarivanja otpora zraka - naš model i formula koju smo izveli ne odgovaraju stvarnosti gdje efekt otpora zraka ima veliki utjecaj.
Greške u ulaznim podacima#
Greške u ulaznim podacima javljaju se zbog nemogućnosti ili besmislenosti točnog mjerenja. Na primjer, tjelesna temperatura se obično mjeri na desetinku stupnja Celzija točno. Pacijent je podjednako loše ako ima temperaturu \(39.5^o\)C ili \(39.513462^o\)C.
Oprez!
Mogu li male greške u ulaznim podacima dovesti do jako velike greške u izlaznim podacima, odnosno, u rezultatu dobivenom na kraju računa?
Nažalost, MOGU! Takvi problemi zovu se loše uvjetovani problemi.
Sada ćemo vidjeti jedan primjer loše uvjetovanog problema, a kasnije ćemo preciznije definirati sam pojam uvjetovanosti.
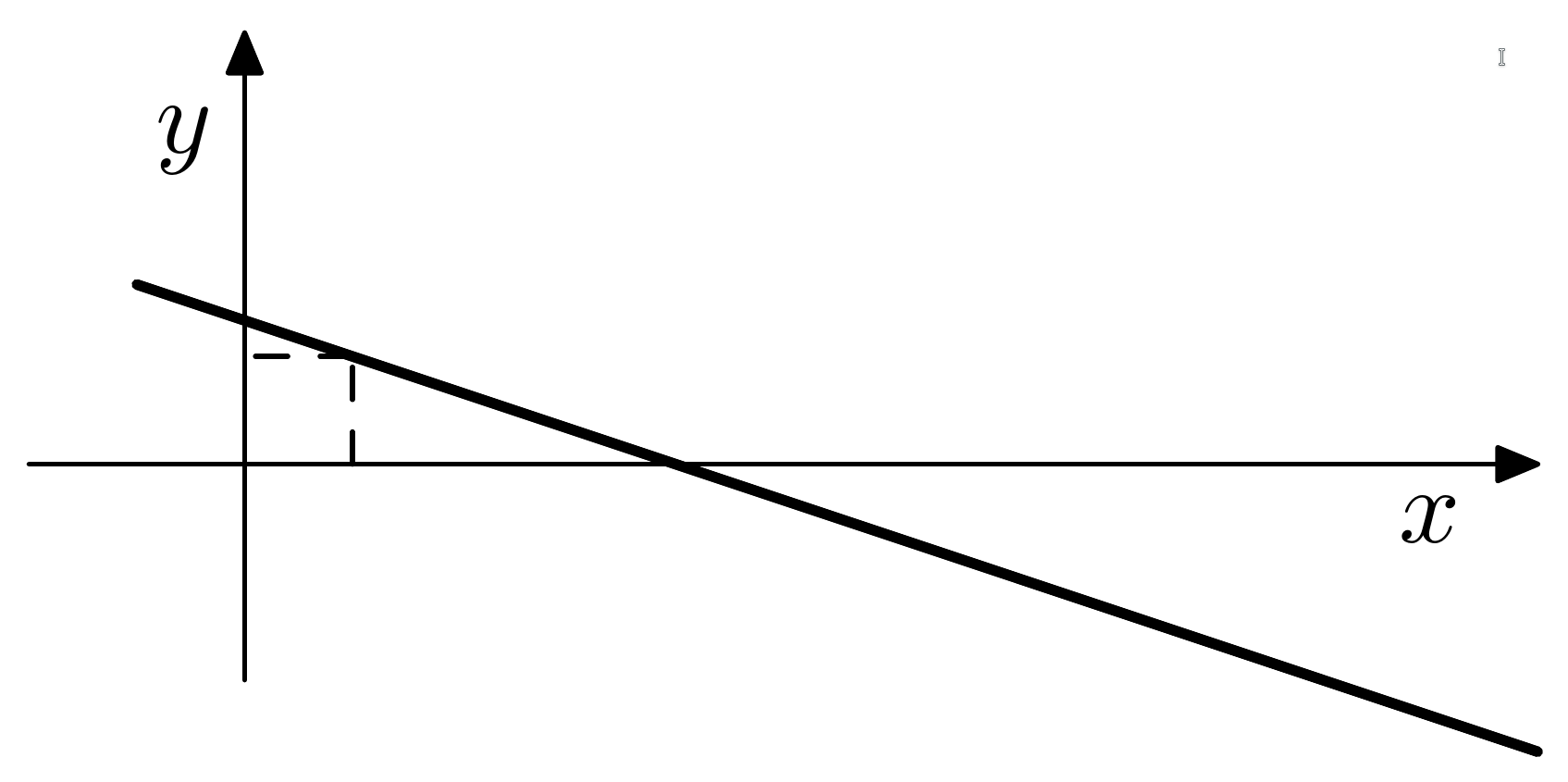
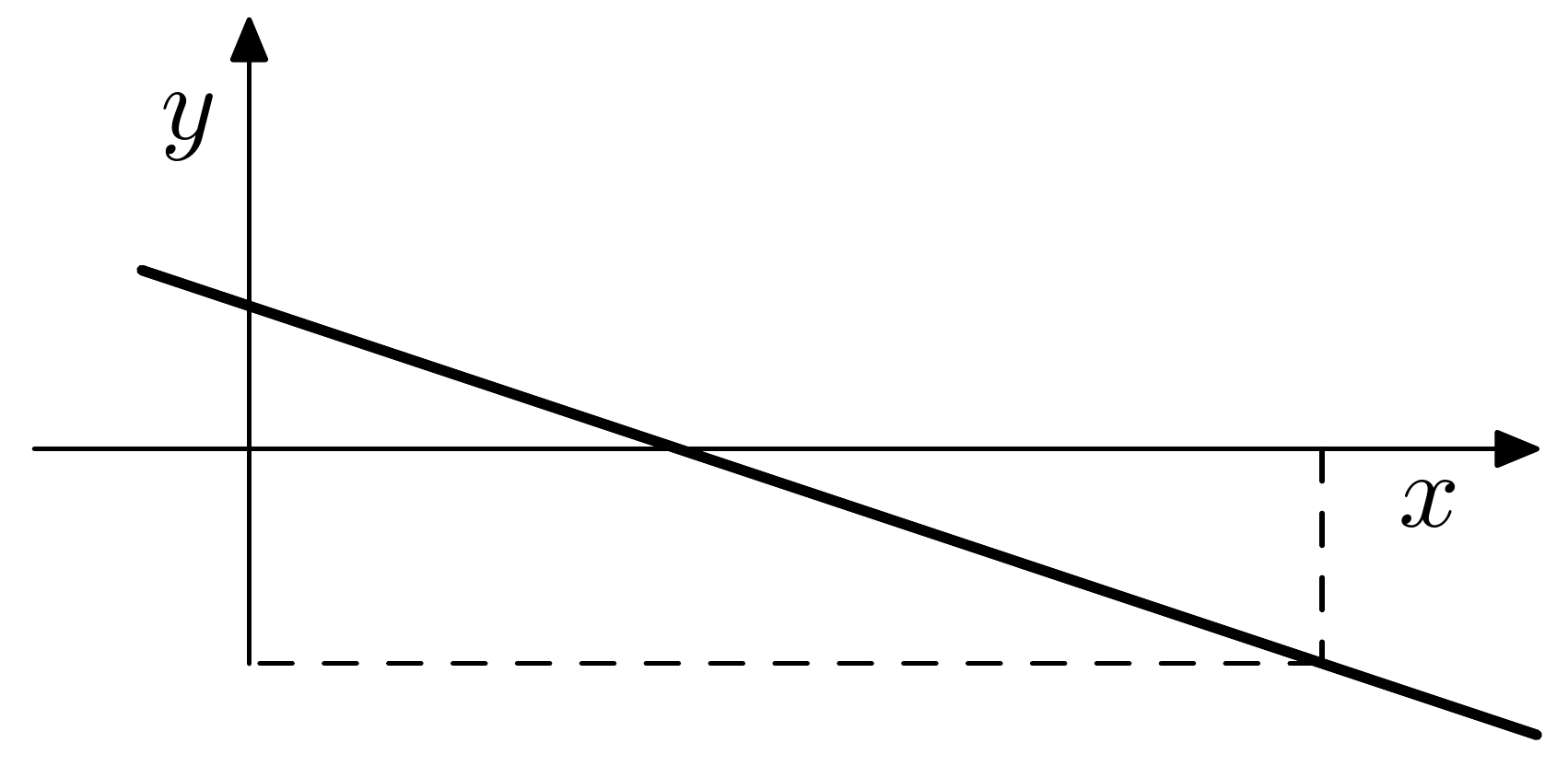
Zamislimo da se neki problem svodi na rješavanje sustava od 2 linearne jednadžbe s 2 nepoznanice čiji koeficijenti dolaze iz mjerenja.
Ako ne napravimo nikakvu grešku u mjerenju, „idealni” sustav bi glasio
Uz minimalne greške u mjerenju koeficijenata druge jednadžbe, zamislimo da izmjereni sustav glasi
Uočimo da je greška u mjerenju samo \(\approx 10^{-4}\). Da li je i razlika u rješenjima \(x\) i \(y\) prvog i drugog sustava također samo \(\approx 10^{-4}\)?
Ne!
Rješenje prvog sustava je \(x = 1\), \(y = 1\).
Rješenje drugog sustava je \(x = 10\), \(y = -2\).
Rješenje drugog sustava se drastično razlikuje od rješenja prvog, iako imaju gotovo identične koeficijente.
Ovo je tipičan primjer tzv. loše uvjetovanog problema: vrlo male promjene ulaznih podataka imaju za posljedicu velike promjene izlaznih podataka. Uzroke loše uvjetovanosti za problem rješavanja sustava linearnih jednadžbi ćemo detaljno razmatrati kasnije. Zasad dajemo samo intuitivno geometrijsko opravdanje: rješenje sustava dobivamo kao presjek dvaju pravaca u ravnini određenih jednadžbama sustava. Na slici lijevo su nacrtana dva (!) pravca koji odgovaraju jednadžbama prvog sustava i označena je točka njihovog presjeka, a na slici desno je isto napravljeno za drugi sustav. U oba slučaju se ti pravci gotovo podudaraju, pa se mjesto presjeka može drastično promijeniti samo malom promjenom koeficijenata.
Greške numeričkih metoda#
Greške numeričkih metoda najčešće nastaju kad se nešto beskonačno zamjenjuje nečim konačnim. Razlikujemo dvije kategorije:
Greške diskretizacije.
Kontinuum (neprebrojiv skup) zamjenjujemo konačnim diskretnim skupom točaka.
Na primjer, rješenje problema \(\min_{x \in [a, b]} f(x)\) aproksimiramo sa \(\min_{x \in \{x_1, x_2, \ldots, x_n\}} f(x)\) za neke \(x_1, \ldots, x_n \in [a, b]\).
Beskonačno malu veličinu \(h\) ili \(\varepsilon \to 0\) zamijenjujemo nekim „konačno” malim brojem.
Na primjer, \(f'(t)\) aproksimiramo sa \(\frac{f(t+h) - f(t)}{h}\) za neki mali \(h\).
Greške odbacivanja.
Iterativni proces koji bi u limesu davao točno rješenje zaustavljamo nakon konačno mnogo koraka.
Beskonačni niz ili red zamjenjujemo konačnim nizom ili parcijalnom sumom, tj. odbacujemo ostatak niza ili reda.
Pokažimo primjerom greške odbacivanja koje nastaju kada koristimo Taylorov red u svrhu računanja aproksimacije vrijednosti funkcije u nekoj točki.
Za dovoljno glatku funkciju \(f\), Taylorov red oko točke \(x_0\)
možemo aproksimirati Taylorovim polinomom
pri čemu smo napravili grešku odbacivanja \(R_{n+1}(x) = f(x) - p(x)\) za koju vrijedi:
Ovdje je \(\xi\) neki broj između \(x_0\) i \(x\).
Funkcije \(e^x\) i \(\sin(x)\) imaju Taylorove redove oko točke \(x_0=0\) koji konvergiraju za svaki \(x \in \R\). Te redove aproksimiramo sa:
Kako znamo izračunati \(n\)-te derivacije: \((e^{x})^{(n)} = e^x\), \((\sin x)^{(n)} = \sin \Big(x + \frac{n \pi}{2} \Big)\), za greške odbacivanja vrijedi
Pretpostavimo sada da je \(x > 0\). Iz \(\xi \leq x\) slijedi \(e^\xi \leq e^x\), pa dobivamo
Pretpostavimo da zbrajamo članove reda sve dok apsolutna vrijednost člana ne padne ispod zadane točnosti \(\varepsilon > 0\), tj. stanimo kada je \(\left|\frac{x^{n+1}}{(n+1)!}\right| < \varepsilon\) za \(e^x\), odnosno, \(\left|\frac{x^{2n+3}}{(2n+3)!}\right| < \varepsilon\) za \(\sin(x)\). Tada za greške odbacivanja vrijedi
to jest
Kasnije ćemo vidjeti da to znači da u prvom slučaju osiguravamo malu relativnu, a u drugom malu apsolutnu grešku. Vidimo da izborom dovoljno malenog \(\varepsilon\) možemo po volji točno aproksimirati vrijednost funkcija \(e^x\) i \(\sin(x)\) uzimanjem dovoljnog broja članova Taylorovog polinoma.
Provjerimo kako teorija iz gornjeg primjera funkcionira u aritmetici računala.
Izračunajmo prvo \(e^{12 \pi}\) uz toleranciju \(\varepsilon = 5 \cdot 10^{-16}\).
Show code cell source
import math;
import matplotlib.pyplot as plt;
def taylor_exp( x, eps ):
clanovi = []; parcijalne_sume = [];
suma = 0.0; clan = 1; k = 0;
while( abs(clan) > eps ):
suma = suma + clan;
clanovi.append( clan );
parcijalne_sume.append( suma );
k = k + 1;
clan = clan * x/k;
return (suma, clanovi, parcijalne_sume);
(suma, clanovi, parcijalne_sume) = taylor_exp( 12*math.pi, 5e-16 );
egzaktna_vrijednost = math.exp(12*math.pi);
print( f'Funkcija exp iz Pythona vraća (egzaktnu) vrijednost: {egzaktna_vrijednost:.16e}.' );
print( f'Vrijednost izračunata pomoću Taylorovog polinoma: {suma:.16e}.' );
print( f'Apsolutna greška: {abs(suma - egzaktna_vrijednost):.16e}.' );
print( f'Relativna greška: {abs(suma - egzaktna_vrijednost) / abs(egzaktna_vrijednost):.16e}.' );
print( f'Taylorov polinom koristi {len(clanovi)} članova.' );
print( f'Najveći član reda (po modulu): {max([abs(c) for c in clanovi]):.5e}.' );
print( f'Teorija daje da je greška odbacivanja manja od: {math.exp(12*math.pi)*5e-16:.5e}.' );
f = plt.figure(figsize=(10,3));
plt.subplot( 1, 2, 1 );
plt.plot( clanovi );
plt.title( 'Članovi reda za exp(12*pi)' );
plt.subplot( 1, 2, 2 );
plt.plot( parcijalne_sume );
plt.title( 'Parcijalne sume reda za exp(12*pi)' );
Funkcija exp iz Pythona vraća (egzaktnu) vrijednost: 2.3578503968558192e+16.
Vrijednost izračunata pomoću Taylorovog polinoma: 2.3578503968558192e+16.
Apsolutna greška: 0.0000000000000000e+00.
Relativna greška: 0.0000000000000000e+00.
Taylorov polinom koristi 131 članova.
Najveći član reda (po modulu): 1.53290e+15.
Teorija daje da je greška odbacivanja manja od: 1.17893e+01.
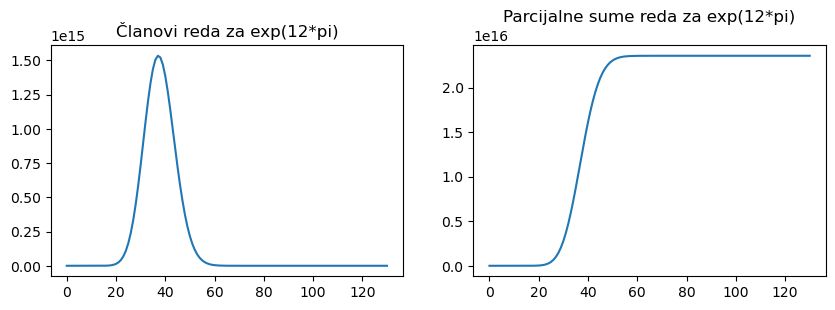
Vidimo da je pomoću Taylorovog reda računalo uspjelo točno izračunati baš sve znamenke od \(e^{12 \pi}\). Uočimo da su svi članovi reda pozitivni brojevi; na slici lijevo vidimo da članovi prvo monotono rastu sve do \(\approx 1.5\cdot 10^{15}\) pa monotono padaju. Na slici desno vidimo da parcijalne sume monotono rastu.
Ponovimo sada numerički eksperiment za \(\sin(12 \pi)\) uz toleranciju \(\varepsilon = 5 \cdot 10^{-16}\).
Show code cell source
def taylor_sin( x, eps ):
clanovi = []; parcijalne_sume = [];
suma = 0.0; clan = x; k = 0;
while( abs(clan) > eps ):
suma = suma + clan;
clanovi.append( clan );
parcijalne_sume.append( suma );
k = k + 1;
clan = clan * (-x*x)/(2*k*(2*k+1.0));
return (suma, clanovi, parcijalne_sume);
(suma, clanovi, parcijalne_sume) = taylor_sin( 12*math.pi, 5e-16 );
egzaktna_vrijednost = math.sin(12*math.pi);
print( f'Funkcija sin iz Pythona vraća (egzaktnu) vrijednost: {egzaktna_vrijednost:.16e}.' );
print( f'Vrijednost izračunata pomoću Taylorovog polinoma: {suma:.16e}.' );
print( f'Apsolutna greška: {abs(suma - egzaktna_vrijednost):.16e}.' );
print( f'Relativna greška: {abs(suma - egzaktna_vrijednost) / abs(egzaktna_vrijednost):.16e}.' );
print( f'Taylorov polinom koristi {len(clanovi)} članova.' );
print( f'Najveći član reda (po modulu): {max([abs(c) for c in clanovi]):.5e}.' );
print( f'Teorija daje da je greška odbacivanja manja od: {5e-16:.5e}.' );
f = plt.figure(figsize=(10,3));
plt.subplot( 1, 2, 1 );
plt.plot( clanovi );
plt.title( 'Članovi reda za sin(12*pi)' );
plt.subplot( 1, 2, 2 );
plt.plot( parcijalne_sume );
plt.title( 'Parcijalne sume reda za sin(12*pi)' );
Funkcija sin iz Pythona vraća (egzaktnu) vrijednost: -1.4695761589768238e-15.
Vrijednost izračunata pomoću Taylorovog polinoma: -4.2275034358615959e-02.
Apsolutna greška: 4.2275034358614488e-02.
Relativna greška: 2.8766821032295473e+13.
Taylorov polinom koristi 65 članova.
Najveći član reda (po modulu): 1.53290e+15.
Teorija daje da je greška odbacivanja manja od: 5.00000e-16.
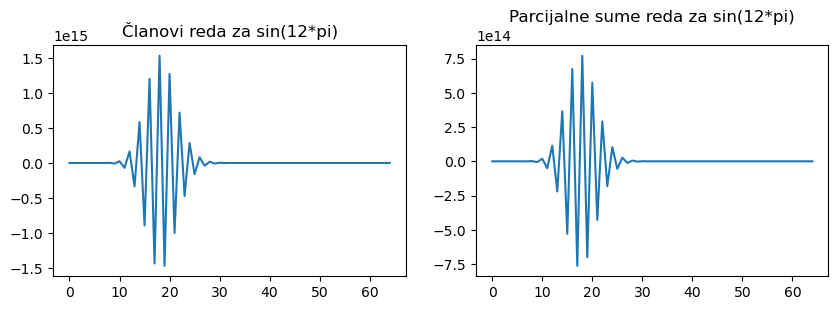
Za razliku od sume za eksponencijalnu funkciju, Taylorov polinom za sinus je dao potpuno pogrešan rezultat! Umjesto očekivane vrijednosti jako blizu nule, dobili smo \(\approx -4.23 \cdot 10^{-2}\), što je u realnoj aritmetici dvostruke točnosti (double) vrlo daleko od nule. Problem je nastao u sljedećem: u sumi se pojavljuju i pozitivni i negativni članovi pri čemu su neki od njih po modulu vrlo veliki (do \(\approx 10^{15}\), vidi sliku lijevo), a konačni rezultat treba ispasti jako maleni broj (\(\approx 0\)). Drugim riječima, konačni rezultat se dobije oduzimanjem bliskih jako velikih brojeva. Objasnit ćemo kasnije zbog čega je ovo veliki problem u aritmetici računala i prototip pojave koja se zove katastrofalno kraćenje.
Velika greška koju smo dobili u primjeru sa sinusom dakle nije posljedica grešaka numeričke metode niti grešaka odbacivanja. Iz (korektne!) teorijske analize koju smo proveli slijedi da bi apsolutna greška \(|\sin(x) - p^{\text{sin}}(x)|\) trebala biti malena (manja od \(5 \cdot 10^{-16}\)). Mogli smo uzeti tisuće ili milijune članova reda za sinus i ponovno bismo dobili isto u eksperimentu na računalu. Neočekivani pogrešni rezultat u ovom slučaju je posljedica grešaka aritmetike računala koje proučavamo u sljedećoj cjelini.