Show code cell source Hide code cell source

import numpy as np;
import scipy as sc;
import matplotlib.pyplot as plt;
from scipy.interpolate import barycentric_interpolate;

%matplotlib inline

3.2. Izbor čvorova interpolacije

U praksi obično koristimo samo interpolacijske polinome niskih stupnjeva - tipično do stupnja 5. Naime, za neke funkcije koje želimo interpolirati, u kombinaciji s nekim izborima čvorova, povećanje stupnja interpolacije može voditi na povećanje grešaka. Uočite da nas sada zanimaju greške interpolacijskog polinoma na cijelom intervalu \([a, b]\) na kojem radimo interpolaciju.

Efekte koji se mogu dogoditi ćemo vidjeti u sljedećih nekoliko primjera. U svima ćemo koristiti ekvidistantnu mrežu čvorova: za odabrani \(n\) u intervalu \([a, b]\) čvorovi su

\[ x_0=a, \; x_1 = a+h, \; x_2 = a+2h, \; \ldots, \; x_k = a + k \cdot h, \; \ldots, \; x_n = a + n \cdot h = b. \]

Ovdje je \(h = \frac{b-a}{n}\) razmak između susjednih čvorova.

Primjer 1. Promotrimo interpolacijske polinome za funkciju \(f(x) = \log_{10}(x)\) na ekvidistantnoj mreži na intervalu \(x \in [0.1, 10]\). Grafovi interpolacijskih polinoma stupnja 1, 3, 5, 8 su redom prikazani u gornjem redu slijeva nadesno, a pripadne greške interpolacije u donjem redu.

Show code cell source Hide code cell source

def interpoliraj( n, graf ):
    # Čvorovi interpolacije: n+1 ekvidistantna točka između 0.1 i 1, uključujući rubove.
    x = np.linspace(0.1, 10, num=n+1);

    # Vrijednosti funkcije f u čvorovima interpolacije.
    f = np.log10(x);  

    # Točke u kojima želimo izračunati vrijednost interpolacijskog polinoma.
    # Uzet ćemo 1000 točaka u intervalu [0.01, 11].
    xx = np.linspace(0.01, 11, num=1000);

    # Vrijednosti interpolacijskog polinoma pomoću funkcije iz biblioteke scipy.
    yy = barycentric_interpolate(x, f, xx);

    # Nacrtamo graf interpolacijskog polinoma i funkcije log(x), te čvorove interpolacije.
    plt.subplot( 2, 4, graf );
    plt.plot(xx, np.log10(xx), 'k-', label='$log_{10}(x)$');
    plt.plot(xx, yy, 'r-', label='p(x)');
    plt.plot(x, f, 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();
    plt.yticks(ticks=[0, -1, 1]);
    plt.title('Ekvidist. mreža, polinom stupnja ' + str(n) + '.');

    # Nacrtamo graf za grešku, te čvorove interpolacije.
    plt.subplot( 2, 4, 4+graf );
    plt.plot(xx, yy-np.log10(xx), 'k-', label='greška $f(x)-p_n(x)$');
    plt.plot(x, np.zeros_like(x), 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();
    plt.yticks(ticks=[0, -1, 1]);
    plt.title('Greška interp., polinom stupnja ' + str(n) + '.');

plt.figure(figsize=[16, 9.6]);

interpoliraj(1, graf=1);
interpoliraj(3, graf=2);
interpoliraj(5, graf=3);
interpoliraj(8, graf=4);

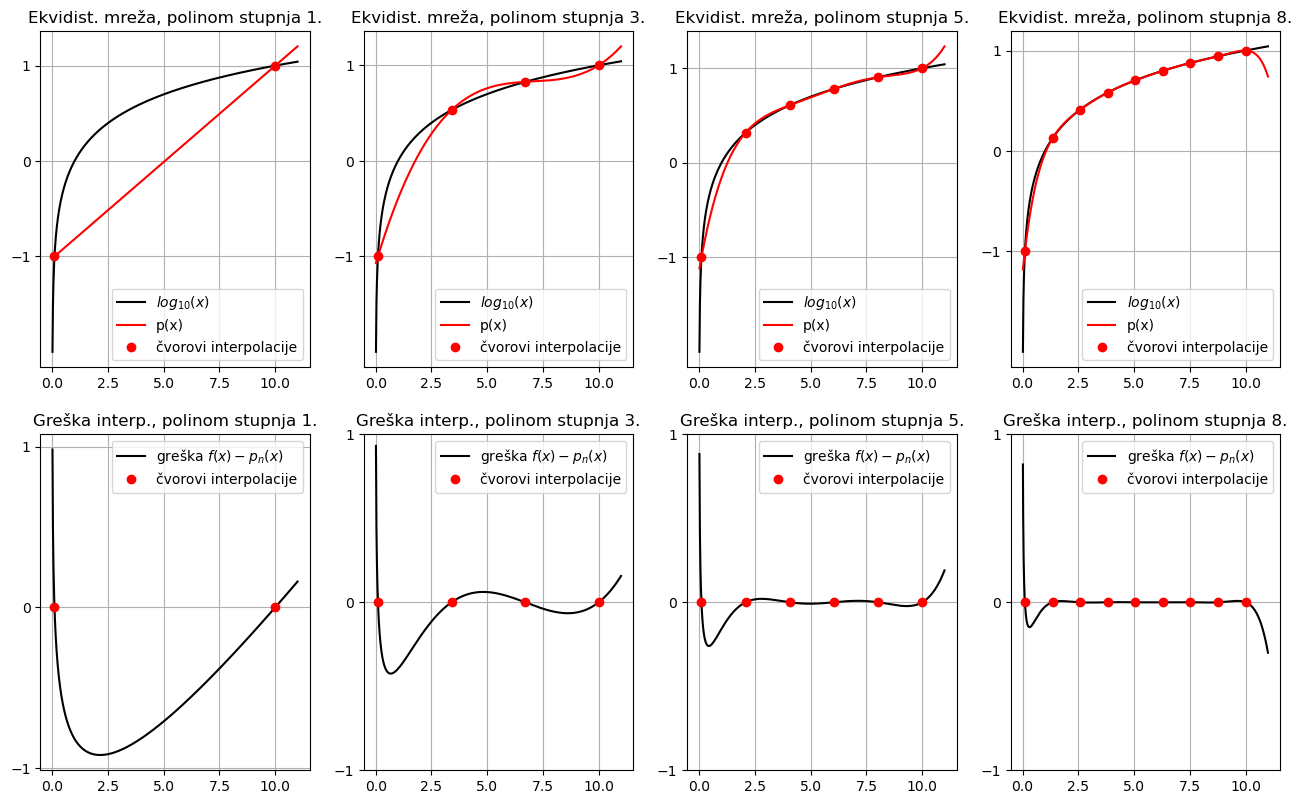
Vidimo da u ovom slučaju povećanje stupnja polinoma vodi na sve bolju interpolaciju funkcije \(f\). Najveća greška je između prva dva čvora interpolacije.

Primjer 2. Promotrimo sada interpolacijske polinome za tzv. Runge funkciju

\[ f(x) = \frac{1}{1+x^2}\]

na ekvidistantnoj mreži na intervalu \([-5, 5]\). Ovu funkciju je 1901. godine konstruirao njemački matematičar Runge s ciljem da niz interpolacijskih polinoma rastućeg stupnja na ekvidistantnim mrežama ne konvergira prema toj funkciji.

Grafovi interpolacijskih polinoma stupnja 2, 5, 10, 16 su redom prikazani u gornjem redu slijeva nadesno, a pripadne greške interpolacije u donjem redu.

Show code cell source Hide code cell source

def interpoliraj( n, graf ):
    # Čvorovi interpolacije: n+1 ekvidistantna točka između 0.1 i 1, uključujući rubove.
    x = np.linspace(-5, 5, num=n+1);

    # Vrijednosti funkcije f u čvorovima interpolacije.
    f = 1 / (1 + x * x);  

    # Točke u kojima želimo izračunati vrijednost interpolacijskog polinoma.
    # Uzet ćemo 1000 točaka u intervalu [-6, 6].
    xx = np.linspace(-6, 6, num=1000);

    # Vrijednosti interpolacijskog polinoma pomoću funkcije iz biblioteke scipy.
    yy = barycentric_interpolate(x, f, xx);

    # Vrijednosti funkcije Runge u točkama xx.
    ff = 1 / (1 + xx * xx);  

    # Nacrtamo graf interpolacijskog polinoma i funkcije Runge, te čvorove interpolacije.
    plt.subplot( 2, 4, graf );
    plt.plot(xx, ff, 'k-', label='f(x)');
    plt.plot(xx, yy, 'r-', label='p(x)');
    plt.plot(x, f, 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();
    plt.ylim(-2, 2);
    plt.yticks(ticks=[0, -1, 1]);
    plt.title('Ekvidist. mreža, polinom stupnja ' + str(n) + '.');

    # Nacrtamo graf za grešku, te čvorove interpolacije.
    plt.subplot( 2, 4, 4+graf );
    plt.plot(xx, yy-ff, 'k-', label='greška $f(x)-p_n(x)$');
    plt.plot(x, np.zeros_like(x), 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();
    plt.ylim(-2, 2);
    plt.yticks(ticks=[0, -1, 1]);
    plt.title('Greška interp., polinom stupnja ' + str(n) + '.');

plt.figure(figsize=[16, 9.6]);

interpoliraj(2, graf=1);
interpoliraj(5, graf=2);
interpoliraj(10, graf=3);
interpoliraj(16, graf=4);

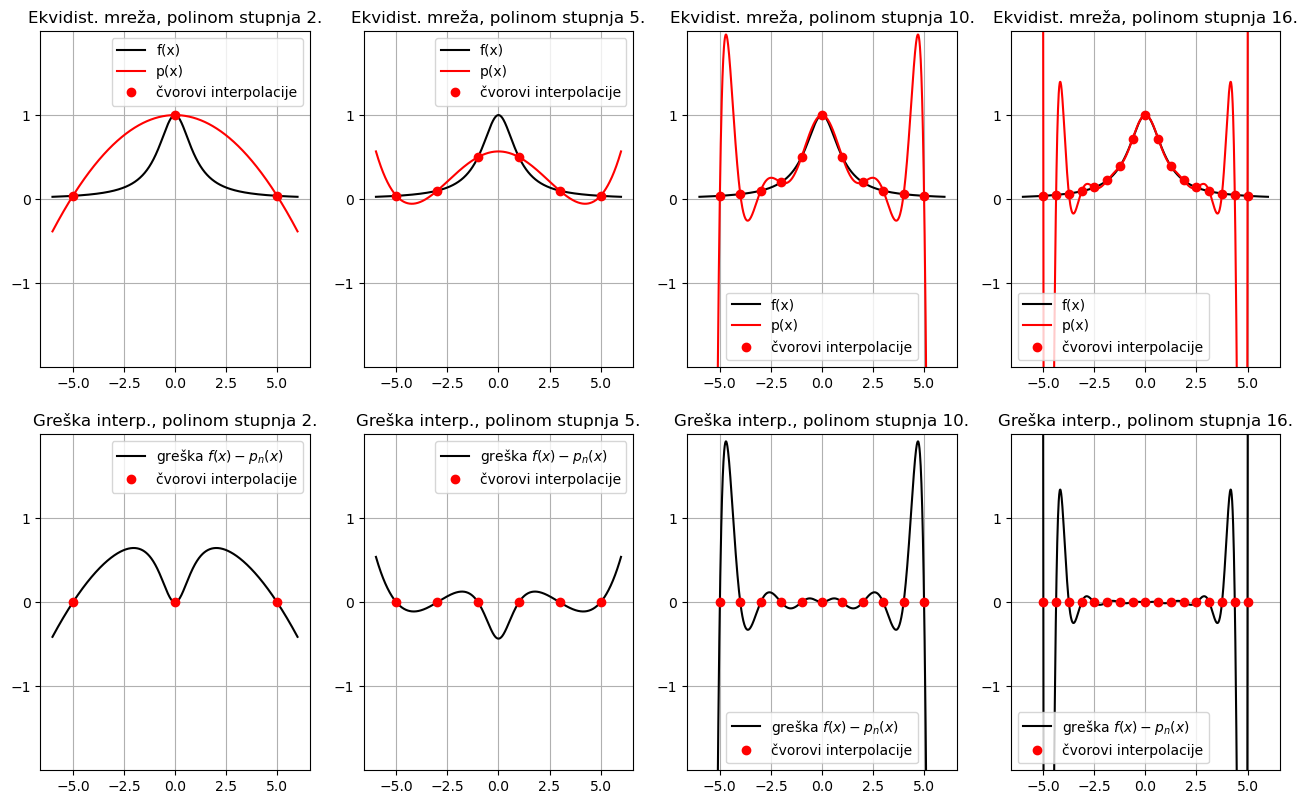
Sada povećanje stupnja polinoma vodi na sve veću i veću grešku između prva dva i zadnja dva čvora interpolacije. Kako \(n\) raste, tako će rasti i maksimalna greška na intervalu interpolacije.

Pažljivom analizom može se pokazati sljedeće:

• za \(|x| > 3.63\), niz \((p_n(x))_{n}\) vrijednosti interpolacijskih polinoma stupnja \(n\) izračunatih u točki \(x\) divergira.

Primjer 3. Promotrimo funkciju

\[ f(x) = |x| \]

i sa \(p_n\) označimo interpolacijski polinom stupnja \(n\) na intervalu \([-1, 1]\) i ekvidistantnoj mreži. Bernstein je 1912. godine uočio da samo za točke \(x = -1, 0, 1\) vrijedi

\[ |f(x)-p_n(x)| \to 0 \; \text{ kada } \; n \to \infty. \]

Za sve ostale \(x \in [-1, 1]\) vrijednost \(p_n(x)\) ne konvergira ka \(f(x)\). Primijetimo da za ovu funkciju ne možemo ocijeniti grešku korištenjem Teorema 3.10 jer ona nije dovoljno glatka.

---

U sva tri primjera koristili smo ekvidistantnu mrežu. Je li neki drugi izbor čvorova bolji?

Definicija 3.16

Za zadani interval \([a, b]\) i \(n \in \N\), Čebiševljevi čvorovi su dani formulom

\[ x_k = \frac{a+b}{2} + \frac{b-a}{2}\cdot \cos\frac{(2(n-k)+1)\pi}{2n+2}, \]

za \(k=0, \ldots, n\).

Primjer 4. Ponovimo numerički eksperiment s Runge funkcijom, ali sada koristeći interpolacijske polinome na Čebiševljevoj mreži na intervalu \([-5, 5]\).

Show code cell source Hide code cell source

def interpoliraj( n, graf ):
    # Čvorovi interpolacije: n+1 čvor Čebiševljeve mreže na [-5, 5].
    a = -5; b = 5;
    x = (a+b)/2 + (b-a)/2 * np.cos( (2*(n - np.arange(n+1))+1)*np.pi / (2*n+2) );

    # Vrijednosti funkcije f u čvorovima interpolacije.
    f = 1 / (1 + x * x);  

    # Točke u kojima želimo izračunati vrijednost interpolacijskog polinoma.
    # Uzet ćemo 1000 točaka u intervalu [-5.5, 5.5].
    xx = np.linspace(-5.5, 5.5, num=1000);

    # Vrijednosti interpolacijskog polinoma pomoću funkcije iz biblioteke scipy.
    yy = barycentric_interpolate(x, f, xx);

    # Vrijednosti funkcije Runge u točkama xx.
    ff = 1 / (1 + xx * xx);  

    # Nacrtamo graf interpolacijskog polinoma i funkcije Runge, te čvorove interpolacije.
    plt.subplot( 2, 4, graf );
    plt.plot(xx, ff, 'k-', label='f(x)');
    plt.plot(xx, yy, 'r-', label='p(x)');
    plt.plot(x, f, 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();
    plt.ylim(-1.5, 1.5);
    plt.yticks(ticks=[0, -1, 1]);
    plt.title('Ekvidist. mreža, polinom stupnja ' + str(n) + '.');

    # Nacrtamo graf za grešku, te čvorove interpolacije.
    plt.subplot( 2, 4, 4+graf );
    plt.plot(xx, yy-ff, 'k-', label='greška $f(x)-p_n(x)$');
    plt.plot(x, np.zeros_like(x), 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();
    plt.ylim(-0.5, 0.5);
    plt.yticks(ticks=[0, -0.5, 0.5]);
    plt.title('Greška interp., polinom stupnja ' + str(n) + '.');

plt.figure(figsize=[16, 9.6]);

interpoliraj(2, graf=1);
interpoliraj(5, graf=2);
interpoliraj(10, graf=3);
interpoliraj(16, graf=4);

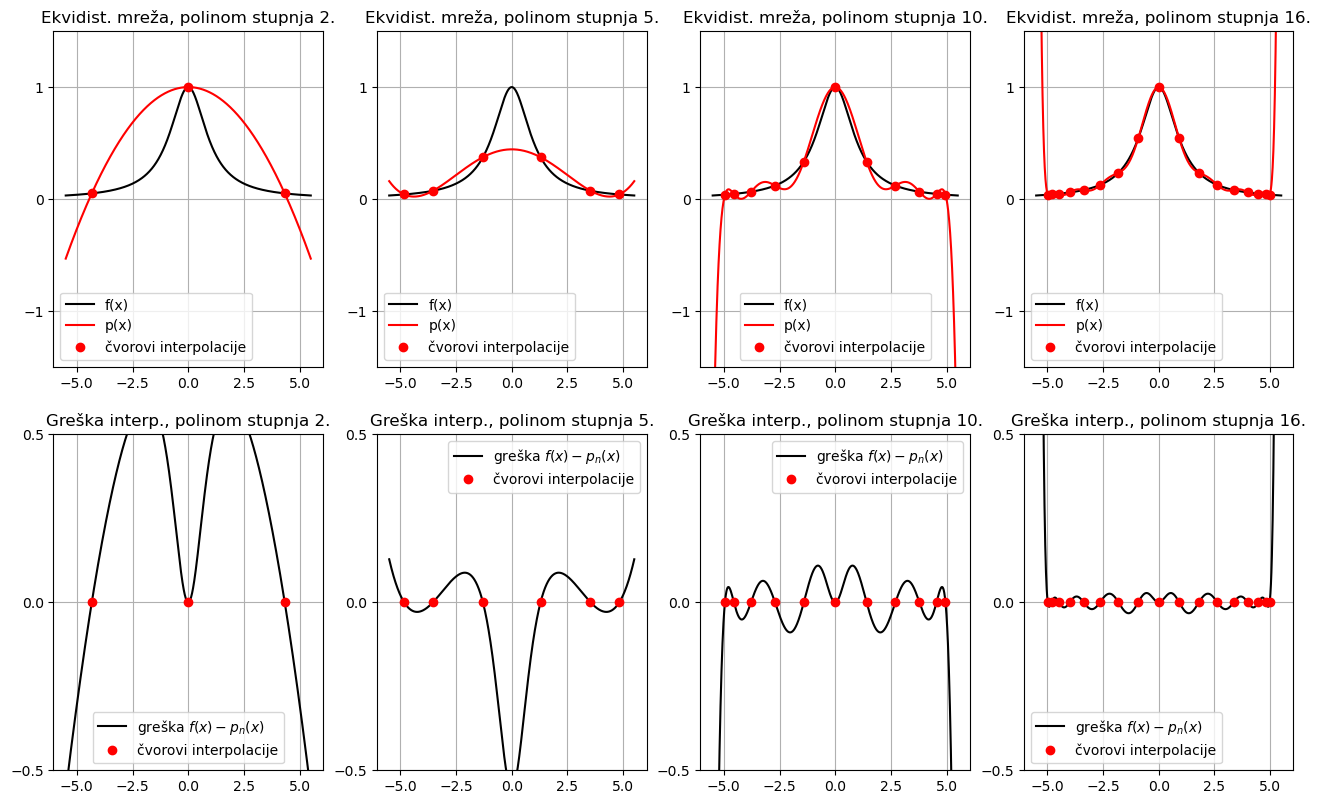
Primjećujemo da greška unutar intervala intepolacije \([-5, 5]\) sada postaje sve manja povećanjem stupnja polinoma; čak smo i smanjili skalu na y-osi u odnosu na graf za ekvidistantne čvorove. Dakle, izbor druge mreže zaista je pomogao u slučaju Runge funkcije. (Uočite da se porast greške na gornjim slikama događa izvan intervala \([-5, 5]\) na kojem radimo interpolaciju.)

Općenito, međutim, nije moguće riješiti ovaj problem i pronaći univerzalnu mrežu koja bi bila dobra za sve funkcije. To pokazuje sljedeći teorem (bez dokaza).

Teorem 3.17 (Faber, 1914.)

Neka je dan proizvoljni niz skupova čvorova

\[ X^{(n)} = \{ x_0^{(n)}, x_1^{(n)}, \ldots, x_n^{(n)} \}, \; n \in \N_0. \]

Tada postoji neprekidna funkcija \(f\), za čiji niz interpolacijskih polinoma \(p_n\) stupnja \(n\), s čvorovima iz skupa \(X^{(n)}\), vrijedi

\[ \|f(x) - p_n(x)\|_{\infty} \not \to 0. \]

Uočite da gornji teorem tvrdi da postoji neprekidna funkcija \(f\) s navedenim svojstvom. Ako zahtijevamo da funkcija \(f\) bude klase barem \(C^1\), tvrdnja teorema više neće vrijediti i postojat će izbor čvorova koji je dobar za svaku takvu funkciju! To će biti upravo Čebiševljevi čvorovi, koje ćemo sada detaljnije proučiti.

Interpolacija u Čebiševljevim točkama

Promotrimo ponovno ocjenu greške za interpolacijski polinom iz Korolara 3.11:

\[ |f(x) - p_n(x)| \leq \frac{|\omega(x)|}{(n+1)!} \max_{x \in [a, b]} |f^{(n+1)}(x)|, \quad x \in [a, b],\]

gdje je \([a, b]\) interval na kojem radimo interpolaciju, a \(w(x) = (x-x_0)(x-x_1)\ldots(x-x_n)\) polinom čvorova. Budući je funkcija \(f\) zadana i na njezinu \((n+1)\)-vu derivaciju ne možemo utjecati, jedini način kako bismo mogli smanjiti desnu stranu (a onda očekivano i lijevu) je da pronađemo čvorove \(x_0, \ldots, x_n\) za koje se postiže što je moguće manja vrijednost izraza

\[ \max_{x \in [a, b]} |w(x)| = \max_{x \in [a, b]} |(x-x_0)(x-x_1)\ldots(x-x_n)|. \]

Drugim riječima, treba pronaći normirani polinom \(p_\ast\) stupnja \(n+1\) takav da je

(3.10)\[ \max_{x \in [a, b]} |p_\ast (x)| = \min_{p \in \mathcal{P}_{n+1} \atop p \text{ normiran}} \max_{x \in [a, b]} |p(x)|.\]

Nultočke polinoma \(p_\ast\) će onda biti čvorovi interpolacije, tj. tada ćemo staviti \(w=p_\ast\). Pomalo iznenađujuće, ali problem (3.10) ima jedinstveno rješenje: optimalni polinom je tzv. Čebiševljev polinom (pomnožen konstantnom tako da bude normiran), a njegove nultočke su dane upravo Definicijom 3.16. Običaj je da se Čebiševljevi polinomi prvo definiraju za interval \([a, b]=[-1, 1]\).

Definicija 3.18 (Čebiševljevi polinomi prve vrste)

Čebiševljevi polinomi prve vrste \(T_n\) su definirani relacijama

\[\begin{split} T_n(x) = \left\{ \begin{array}{ll} \cos (n \cdot \arccos(x)), & x \in [-1, 1], \\ \cosh (n \cdot \text{arcCosh}(x)), & |x| \geq 1. \\ \end{array} \right. \end{split}\]

Da je funkcija \(T_n\) iz gornje definicije zaista polinom stupnja \(n\), lako slijedi indukcijom iz sljedeće propozicije (dokažite i nju indukcijom koristeći adicione formule za \(\cos\) i \(\cosh\)!)

Propozicija 3.19 (Tročlana rekurzija za Čebiševljeve polinome)

Funkcije \(T_n\) zadovoljavaju tročlanu rekurziju, za sve \(x \in \R\):

\[\begin{split} \begin{align*} T_0(x) &= 1, \\ T_1(x) &= x, \\ T_{n+1}(x) - 2x T_n(x) + T_{n-1}(x) &= 0. \end{align*} \end{split}\]

Nije teško izračunati nultočke ni ekstreme polinoma \(T_{n+1}\) (uočite da ćemo promatrati njega a ne \(T_n\) jer nam treba \(n+1\) nultočaka koje će biti čvorovi interpolacije).

Propozicija 3.20 (Nultočke i ekstremi Čebiševljevog polinoma \(T_{n+1}\))

Nultočke polinoma \(T_{n+1}\) su dane sa:

\[ x_k = \cos \frac{(2k+1) \pi}{2(n+1)}, \quad k=0, 1, \ldots, n. \]

Nultočke su indexirane u silazanom poretku. Minimalna vrijednost polinoma \(T_{n+1}\) na intervalu \([-1, 1]\) je jednaka \(-1\), a maksimalna je jednaka \(1\). Ekstremi na intervalu \([-1, 1]\) se postižu u (silazno sortiranim) točkama

\[ x_k' = \cos \frac{k \pi}{n+1}, \quad k=0, 1\ldots, n+1, \]

pri čemu je vrijednost u ekstremu jednaka \(T_{n+1}(x_k') = (-1)^k\). Ekstrema ima točno \(n+2\), što uključuje i rubove intervala \(x_0' = 1\) i \(x_{n+1}' = -1\).

Show code cell source Hide code cell source

import numpy as np;
import matplotlib.pyplot as plt;
import numpy.polynomial.chebyshev as chebpoly;

n = 6;

# Uzmimo 100 ekvidistantnih x-eva u [-1.02, 1.02].
x = np.linspace( -1.02, 1.02, 100 );

# Izračunamo vrijednost Čebiševljevog polinoma T_(n+1) u svim tim točkama.
koef = np.zeros( n+2 ); koef[n+1] = 1; # koef = [0, 0, 0, 0, 0, 0, 0, 1].
px = chebpoly.chebval( x, koef );

# Nacrtamo graf od T_7.
plt.figure();
plt.plot( x, px, 'k', label='$T_7(x)$' );
plt.grid();

# Nultočke.
x_nultocke = np.cos( (2*np.arange(0, n+1) + 1.0) * np.pi / (2*(n+1)) );
plt.plot( x_nultocke, np.zeros(n+1), 'ro', label='nultočke $x_k$' );

# Ekstremi.
x_ekstremi = np.cos( np.arange(0, n+2) * np.pi / (n+1) );
px_ekstremi = chebpoly.chebval( x_ekstremi, koef );
plt.plot( x_ekstremi, px_ekstremi, 'bo', label='ekstremi $x_k\'$' );

plt.legend();
plt.title( 'Nultočke i ekstremi Čebiševljevog polinoma $T_7$' );

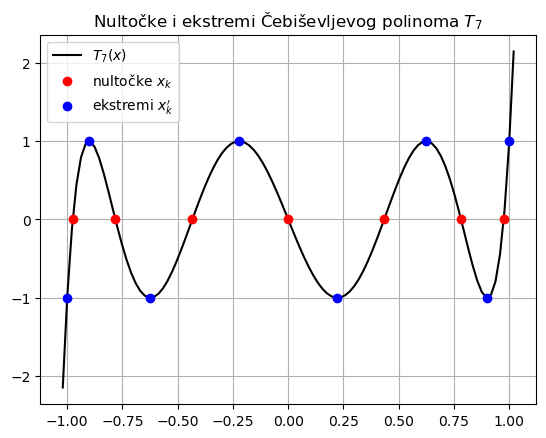
Na slici vidimo kako Čebiševljev polinom na intervalu \([-1, 1]\) ima graf koji nas može donekle podsjećati na funkciju kosinus, što je i očekivano iz definicije. Vrijednosti polinoma osciliraju između minimuma \(-1\) i maksimuma \(1\), a sve nultočke od \(T_{n+1}\) su realne i nalaze se unutar \([-1, 1]\). Čim izađemo iz intervala \([-1, 1]\), vrijednost od \(T_{n+1}(x)\) brzo eksplodira.

Pokažimo sada i obećani rezultat koji opravdava korištenje nultočki Čebiševljevih polinoma kao čvorova u interpolaciji. Radi jednostavnije notacije, teorem iskazujemo za polinom \(T_n\), a kao čvorove ćemo koristiti nultočke polinoma \(T_{n+1}\).

Teorem 3.21 (Optimalnost Čebiševljevih polinoma)

Za zadani prirodni broj \(n\), promotrimo minimizacijski problem

\[ \tau_n := \inf_{p \in \mathcal{P}_{n} \atop p \text{ normiran}} \max_{x \in [-1, 1]} |p(x)|. \]

Vrijedi \(\tau_n = \frac{1}{2^{n-1}}\), a infimum se i dostiže i to samo za polinom

\[ p(x) = \frac{1}{2^{n-1}} T_n(x). \]

Dokaz.

Iz tročlane rekurzije lako slijedi (indukcija!) da vodeći koeficijent polinoma \(T_n\) iznosi \(2^{n-1}\). Stoga je \(\frac{1}{2^{n-1}} T_n\) normirani polinom stupnja \(n\) za kojeg, prema Propoziciji 3.20 vrijedi

\[ \max_{x \in [-1, 1]} \left| \frac{1}{2^{n-1}} T_n(x) \right| = \frac{1}{2^{n-1}}. \]

Stoga je \(\tau_n \leq \frac{1}{2^{n-1}}\). Pretpostavimo da vrijedi stroga nejednakost, tj. da postoji normirani polinom \(M\) stupnja \(n\) za kojeg je

\[ \tau_n \leq \max_{x \in [-1, 1]}|M(x)| < \frac{1}{2^{n-1}}. \]

Označimo \(R(x) := \frac{1}{2^{n-1}}T_n(x) - M(x)\). Kako je riječ o razlici normiranih polinoma, koeficijent uz \(x^n\) se poništi pa je stupanj polinoma \(R\) manji ili jednak \(n-1\). Promotrimo vrijednosti polinoma \(R\) u lokalnim ekstremima \(x_0', x_1', \ldots, x_n'\) Čebiševljevog polinoma:

\[\begin{split} \begin{align*} R(x_0') &= R(1) = \frac{1}{2^{n-1}} - M(1) \red{> 0} \\ R(x_1') &= \frac{-1}{2^{n-1}} - M(x_1') \red{< 0} \\ R(x_2') &= \frac{1}{2^{n-1}} - M(x_2') \red{> 0} \\ &\vdots \end{align*} \end{split}\]

Vidimo da vrijedi \(\text{sign}(R(x_k')) = (-1)^k\), \(k=0, 1, \ldots, n\). Zbog neprekidnosti polinoma \(R\), postoje točke \(\xi_1 \in \langle x_1', x_0' \rangle\), \(\xi_2 \in \langle x_2', x_1' \rangle\), …, \(\xi_n \in \langle x_n', x_{n-1}' \rangle\) u kojima \(R\) poprima vrijednost \(0\). Dakle, polinom \(R\) stupnja \(\leq n-1\) ima barem \(n\) nultočki \(\xi_1, \ldots, \xi_n\). To je moguće jedino u slučaju da je \(R\) nul-polinom, odnosno,

\[ M(x) = \frac{1}{2^{n-1}} T_n(x), \]

pa je i \(\max_{x \in [-1, 1]} M(x) = \frac{1}{2^{n-1}}\), što je kontradikcija s pretpostavkom. Dakle, \(\tau_n = \frac{1}{2^{n-1}}\). Još preostaje dokazati da je \(\frac{1}{2^{n-1}} T_n(x)\) jedini polinom za koji se postiže jednakost. Taj dokaz je vrlo sličan gornjem pa ga prepuštamo studentima.

Uzimanjem nultočki \(x_0, \ldots, x_n\) Čebiševljevog polinoma \(T_{n+1}\) kao čvorova interpolacije slijedi

\[ \max_{x \in [-1, 1]} |w(x)| = \max_{x \in [-1, 1]} |(x-x_0)(x-x_1)\ldots (x-x_n)| = \max_{x \in [-1, 1]} \left|\frac{1}{2^n} T_{n+1}(x)\right| = \frac{1}{2^n}. \]

Čebiševljevi polinomi na proizvoljnom intervalu \([a, b]\)

Afino preslikavanje

\[ \varphi(x) = \frac{a+b}{2} + \frac{b-a}{2}x, \quad x \in [-1, 1] \]

preslikava interval \([-1, 1]\) na interval \([a, b]\), a njegov inverz

\[ \psi(x) := \varphi^{-1}(x) = \frac{2}{b-a}x - \frac{a+b}{b-a}, \quad x \in [a, b]. \]

naravno preslikava \([a, b]\) na \([-1, 1]\). Lako se vidi (dokažite!) da se infimum

\[ \inf_{p \in \mathcal{P}_n \atop p \text{ normiran}} \max_{x \in [a, b]} |p(x)| \]

postiže za polinom koji dobijemo normiranjem polinoma \(T_n(\psi(x))\). Stoga su (dokažite!) čvorovi interpolacije polinomom stupnja \(n\) kojima se minimizira \(\max_{x \in [a, b]} |w(x)|\) dani sa

\[ \tilde{x}_k = \varphi(x_k) = \frac{a+b}{2} + \frac{b-a}{2} \cos \frac{(2k+1)\pi}{2(n+1)}, \quad k=0, \ldots, n. \]

Ovo se, uz obrnutu indeksaciju, podudara s Definicijom 3.16 Čebiševljevih čvorova.

Za kraj ove cjeline, bez dokaza navodimo rezultat o uniformnoj konvergenciji niza interpolacijskih polinoma na Čebiševljevoj mreži.

Teorem 3.22 (Uniformna konvergencija interpolacijskih polinoma na Čebiševljevoj mreži)

Neka je \(f \in C^1([-1, 1])\) proizvoljna funkcija. Za svaki \(n \in \mathbb{N}\), neka je \(p_n\) interpolacijski polinom za funkciju \(f\) na Čebiševljevoj mreži s \(n+1\) čvorova na intervalu \([-1, 1]\).

Tada niz polinoma \((p_n)_n\) uniformno konvergira prema \(f\) na \([-1, 1]\), tj. vrijedi

\[ \lim_{n} \|f - p_n\|_\infty = \lim_n \max_{x \in [-1, 1]} |f(x) - p_n(x)| = 0. \]

Ovdje ne bi bilo dovoljno pretpostaviti samo neprekidnost funkcije \(f\) – to bi bilo u suprotnosti s Faberovim Teoremom 3.17. Dokaz gornjeg teorema i puno šira diskusija o interpolaciji polinomima može se pronaći u [Tre13].

Chebfun

Gornji teorem omogućava da račun s proizvoljnom funkcijom iz \(C^1\) (npr. traženje nultočki, deriviranje, integriranje, rješavanje diferencijalnih jednadžbi) zamijenimo bitno jednostavnijim računom s polinomom dovoljno visokog stupnja koji tu funkciju interpolira na Čebiševljevoj mreži.

Ova ideja je realizirana u biblioteci chebfun koja je originalno implementirana u Matlabu, no postoje i implementacije u Pythonu. Pažljivom implementacijom (npr. korištenjem baricentričke formule) i detaljnom numeričkom analizom izbjegnuti su numerički problemi koji se mogu javiti kod korištenja polinoma vrlo visokog stupnja. Na ovaj način moguće je aproksimativno i efikasno riješiti neke probleme koje bi bilo vrlo teško riješiti s originalnom funkcijom.

Literatura

[Tre13]

Lloyd N. Trefethen. Approximation Theory and Approximation Practice. SIAM, 2013.