Show code cell source
import numpy as np;
import scipy as sc;
import matplotlib.pyplot as plt;
from scipy.optimize import curve_fit;
%matplotlib inline
4.1. Diskretni problem najmanjih kvadrata#
Opis problema Za zadanu funkciju \(f: X \to \R\) cilj je naći što bolju aproksimacijsku funkciju \(\varphi\) među svim funkcijama \(\psi\) iz određenog skupa \(\mathcal S\). U slučaju da raspolažemo nekom normom \(\| \cdot \|\), tražimo \(\varphi \in \mathcal S\) takvu da je
Za razliku od problema interpolacije iz prošlog poglavlja, kriterij „bliskosti” nije u tome da funkcije \(\varphi\) i \(f\) imaju jednako djelovanje na diskretnom skupu podataka, nego da je im je udaljenost (norma razlike) što manja moguća, ali u pravilu različita od nule.
Gore opisani problem je teško zamisliti jer je dan u najvećoj mogućoj općenitosti. U ovoj lekciji pretpostavljamo sljedeće:
\(X\) će biti diskretan skup \(\{ t_1, t_2, \dots, t_n \} \subset \R\) - u tom slučaju gornji problem zove se diskretni problem najmanjih kvadrata;
\(\mathcal S\) će biti neki vektorski prostor \(V\) (najlakše je razmišljati kao prostor polinoma \(\mathcal P_m\)) – u tom slučaju pokazat će se da ovaj problem možemo riješiti eksplicitno koristeći alate iz linearne algebre, što inače nije slučaj za generalni izbor skupa \(\mathcal S\);
norma na domeni \(X\) bit će dana kao Euklidska norma u istaknutim točkama domene:
dimenzija vektorskog prostora \(V\) \(m\) bit će (mnogo) manja od broja čvorova \(n\) u domeni \(X\).
Još pojednostavljenije, pogledajmo jedan konkretan primjer.
Klasičan problem najmanjih kvadrata je odrediti pravac \(y=ax+b\) (tj. odrediti realne koeficijente \(a,b\)) koji najbolje određuje funkciju zadanu skupom podataka \((x_i,y_i)\), \(i=1,\dots,n\). Za ovaj primjer, neka su ti brojevi dani u tablici:
\(i\) |
\(x_i\) |
\(y_i\) |
|---|---|---|
\(1\) |
\(1.0\) |
\(2.5\) |
\(2\) |
\(2.0\) |
\(3.7\) |
\(3\) |
\(3.0\) |
\(3.5\) |
\(4\) |
\(4.0\) |
\(4.5\) |
\(5\) |
\(5.0\) |
\(4.9\) |
Dakle, u ovom primjeru imamo
\(X = \{ x_1,\dots,x_n\}\);
\(\mathcal S = V = \{ ax+b \ : \ a,b \in \mathbb R \} = \mathcal P_1\);
funkcija \(f:X \to \R\) definirana je djelovanjem na domeni \(X\) pravilom \(f(x_i) = y_i\), \(i=1,\dots,n\).
Tražimo \(\varphi (x) = ax+b\) takvu da je norma \(\|f - \varphi\|\) što manja. Za nju vrijedi
Cilj je odrediti \(a,b \in \R\) koji minimiziraju \(S(a,b)\), uz gore definiranu funkciju \(S:\R^2 \to \R\). To možemo tehnikama diferencijalnog računa više varijabli. Nađimo stacionarnu točku tako da izjednačimo parcijalne derivacije s nulom. Koristeći da je derivacija sume jednaka sumi derivacija, dobivamo
Dobili smo linearan sustav po \(a,b\). Nakon djeljenja s \(2\), matrični zapis tog sustava je
Uvrštavanjem vrijednosti iz podataka, dobivamo rješenje
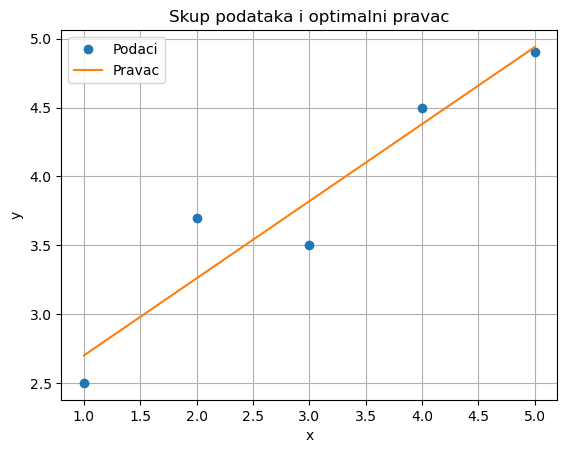
Dakle, rješenje ovog problema je pravac
Da bi dokaz bio potpun, trebalo bi dokazati da je ova stacionarna točka ujedno i globalni minimum. To se može opravdati tako da se dokaže da je funkcija \(S\) konveksna gledajući njezinu drugu derivaciju, ili tako da se vidi da je graf funkcije \(S\) paraboloid, ili se možemo nasloniti na teoriju koju ćemo odraditi kasnije.
Rješenje u pythonu:
Show code cell source
def LinearniNajmanjiKvadrati (x,y):
# Izrada sustava jednadžbi
n = len(x)
A = np.zeros((2, 2))
B = np.zeros(2)
A [0,0] = np.sum(x[:] * x[:])
A [1,0] = np.sum(x[:])
A [0,1] = np.sum(x[:])
A [1,1] = n
B[0] = np.sum(x[:] * y[:])
B[1] = np.sum(y[:])
#Rješavanje sustava
rj = np.linalg.solve(A,B)
a = rj[0]
b = rj[1]
return a,b
# Zadani podaci
x = np.array([1, 2, 3, 4, 5])
y = np.array([2.5, 3.7, 3.5, 4.5, 4.9])
a,b = LinearniNajmanjiKvadrati(x,y)
# Ispis rezultata
print("Vrijednost a:", a)
print("Vrijednost b:", b)
Vrijednost a: 0.5599999999999993
Vrijednost b: 2.1400000000000023
Show code cell source
# Dio koda za vizualizaciju
def model(x, a, b):
return a * x + b
x_line = np.linspace(min(x), max(x), 100)
y_line = model(x_line, a, b)
plt.plot(x, y, 'o', label='Podaci')
plt.plot(x_line, y_line, label='Pravac')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Skup podataka i optimalni pravac')
plt.legend()
plt.grid(True)
plt.show()
Pokažimo jedan primjer u kojem \(\mathcal S\) nije vektorski prostor. Slično, kao u prošlom primjeru, nađimo najbolju aproksimacijsku funkciju \(f\) na domeni \(X = \{ x_1,\dots,x_n\}\), s vrijednostima \(f(x_i) = y_i\), gdje su podatci dani u tablici.
\(i\) |
\(x_i\) |
\(y_i\) |
|---|---|---|
\(1\) |
\(1.0\) |
\(5.0\) |
\(2\) |
\(2.0\) |
\(6.0\) |
\(3\) |
\(3.0\) |
\(17.0\) |
\(4\) |
\(4.0\) |
\(58.0\) |
\(5\) |
\(5.0\) |
\(145.0\) |
Razlika je u tome što tražimo aproksimaciju u formatu \(\varphi(x) = a e^{bx}\). Skup takvih funkcija, za razne \(a,b\), nije vektorski prostor. Možemo pokušati rješavati na isti način. Za normu razlike funkcija \(f\) i \(\varphi\) vrijedi
Cilj je ponovno odrediti \(a,b \in \R\) koji minimiziraju \(S(a,b)\), uz gore definiranu funkciju \(S:\R^2 \to \R\), što ponovno radimo tražeći stacionarnu točku.
Došli smo do sustava nelinearnih jednadžbi po \((a,b)\). Čak i da uvedemo susptituciju za \(e^b\), parametri iz podataka \(x_i\) nalaze se u eksponentima te nepoznanice što čini problem nerješivim analitički. Sustav zato možemo riješiti samo aproksimativno nekim numeričkim alatima koje još nismo radili, dakle ne znamo eksplicitno rješenje ovog sustava. Ispostavlja se da je aproksimacija tog rješenja dana s
čime smo dobili aproksimacijsku funkciju
Ono što se u praksi često radi je da se nelinearni problemi lineariziraju. Konkretno u ovom slučaju, nećemo tražiti funkciju \(f\) takvu da je \(f\approx \varphi\), nego ćemo na obje strane primijeniti prirodni logaritam, te tražiti da je
Došli smo do linearnog problema najmanjih kvadrata
uz oznake
Dakle, uvjeti su isti kao u prvom primjeru. Nakon transformacije podataka, tablica je sada
\(i\) |
\(\tilde x_i\) |
\(\tilde y_i\) |
|---|---|---|
\(1\) |
\(1.0\) |
\(1.60943791\) |
\(2\) |
\(2.0\) |
\(1.79175947\) |
\(3\) |
\(3.0\) |
\(2.83321334\) |
\(4\) |
\(4.0\) |
\(4.06044301\) |
\(5\) |
\(5.0\) |
\(4.97673374\) |
Ponavljajući postupak kao u prvom primjeru, dobivamo
čime smo dobili aproksimacijsku funkciju
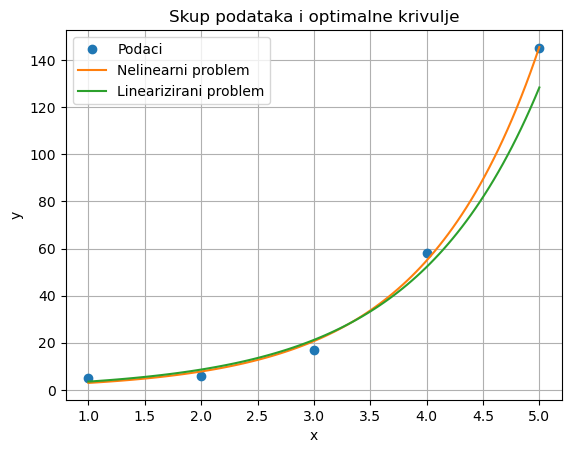
drugačiju od one kada smo rješavali nelinearan problem najmanjih kvadrata.
Rješenje u pythonu:
Show code cell source
# Zadani podaci
x = np.array([1, 2, 3, 4, 5])
y = np.array([5, 6, 17, 58, 145])
# Definiranje funkcije modela
def model(x, a, b):
return a * np.exp(b * x)
# Pronalaženje optimalnih parametara
popt, pcov = curve_fit(model, x, y)
a = popt[0]
b = popt[1]
# Ispis rezultata
print("Vrijednost a iz nelinearnog problema:", a)
print("Vrijednost b iz nelinearnog problema:", b)
# Transformacije za linearizaciju
xt = x
yt = np.log(y)
at,bt = LinearniNajmanjiKvadrati(xt,yt)
print("Vrijednost tilda a: ", at)
print("Vrijednost tilda b: ", bt)
aL = np.exp(bt)
bL = at
print("Vrijednost a iz lineariziranog problema:", aL)
print("Vrijednost b iz lineariziranog problema:", bL)
# Dio koda za vizualizaciju
x_line = np.linspace(min(x), max(x), 100)
y_line = model(x_line, a, b)
z_line = model(x_line, aL, bL)
plt.plot(x, y, 'o', label='Podaci')
plt.plot(x_line, y_line, label='Nelinearni problem')
plt.plot(x_line, z_line, label='Linearizirani problem')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Skup podataka i optimalne krivulje')
plt.legend()
plt.grid(True)
plt.show()
Vrijednost a iz nelinearnog problema: 1.1087915286620755
Vrijednost b iz nelinearnog problema: 0.9755090807668448
Vrijednost tilda a: 0.9003275201291302
Vrijednost tilda b: 0.35333493534968247
Vrijednost a iz lineariziranog problema: 1.4238079471926013
Vrijednost b iz lineariziranog problema: 0.9003275201291302
Treba naglasiti da linearizacijom rješavamo problem koji nije ekvivalentan nelinearnom problemu najmanjih kvadrata. Ipak, u praksi se često pokazuje da lineariziranim problemom dobivamo rješenje koje je za primjenu dovoljno dobro, metodom koja je mnogo povoljnija od nelinearnog pristupa. Zato nadalje promatramo samo linearne probleme najmanjih kvadrata.
Matrični zapis diskretnog problema najmanjih kvadrata#
Kako je \(\mathcal S\) vektorski prostor, nađimo mu bazu \(\{ \varphi_1, \dots, \varphi_m\}\). Zadatak je naći funkciju
koja najbolje aproksimira funkciju \(f : \{ t_1, \dots, t_n\} \to \R\) određenu s \(f(t_i) = y_i\).
Uvedimo matricu \(A \in \R^{n \times m}\) takvu da je \(a_{i,j} = \varphi_j(t_i)\) i vektor \(b \in \R^n\) takav da je \(b_i = y_i\), za sve \(i,j\). Tada je cilj minimizirati
gdje je zadnja norma Euklidska norma na \(\R^n\). Dakle, početni problem zapisali smo pomoću pojmova linearne algebre: za dane \(A \in \R^{n \times m}\) i \(b \in \R^n\) potrebno je pronaći vektor \(x \in \R^m\) takav da je norma \(\| Ax - b \|_2\) najmanja moguća.
Ako je \(m\geq n\) (i ako su retci od \(A\) linearno nezavisni), tada je moguće naći \(x\) takav da je \(Ax = b\) (za \(m=n\) to je rješavanje kvadratnog sustava). Zato smo pretpostavili da je \(m<n\). Nadalje radi jednostavnosti pretpostavljamo i da je \(A\) punog stupčanog ranga \(r(A) = m\) (iako se teorija može relativno proširiti i u generalnijem smjeru).
Ovom problemu sada možemo pristupiti alatima linearne algebre i dokazati egzistenciju i jedinstvenost.
Neka je \(m<n\), matrica \(A \in \R^{n \times m}\) ranga \(m\) i neka je dan vektor \(b \in \R^n\). Tada postoji jedinstveni \(x\in \R^m\) takav da je \(\| Ax - b \|_2\) najmanje moguće. Taj \(x\) zadovoljava
te je jedinstveno rješenje sustava normalnih jednadžbi
Napomena
Ako ne pretpostavimo da je matrica \(A\) punog ranga, i dalje vrijedi egzistencija, ali nemamo jedinstvenost.
Korak 1. Promotrimo bilo koji \(x \in \R^m\) sa svojstvom (4.1). U ovom koraku promatramo samo svojstva takvog vektora, za koji još ne znamo ni postoji li. Dokazat ćemo da za svaki drugi vektor \(\hat x \in \R^m\) različit od \(x\) vrijedi
čime ćemo dokazati da je \(x\) s takvim svojstvom jedinstven, te je (ako postoji) jedinstveno rješenje matričnog problema najmanjih kvadrata.
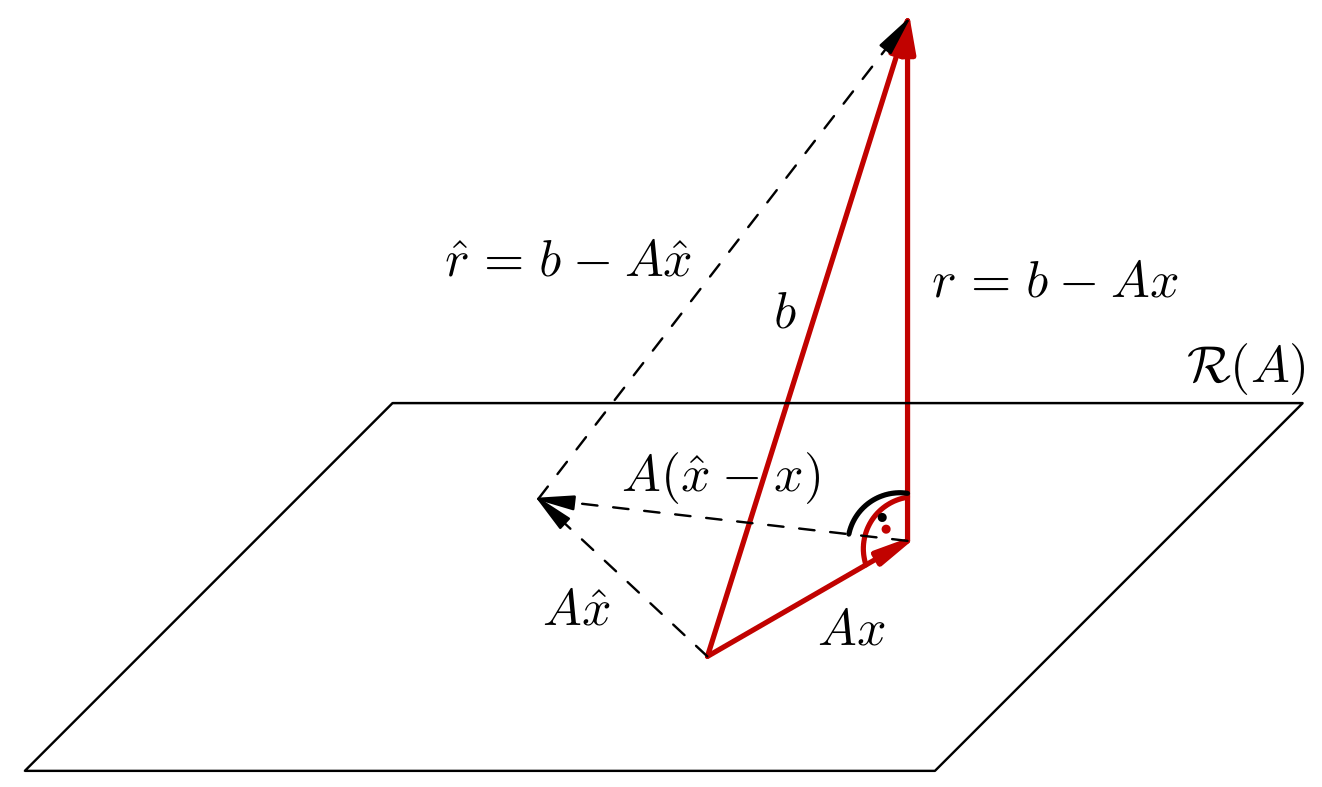
Vektor \(A(\hat x - x)\) pripada slici \(\mathcal R(A)\), pa je prema svojstvu (4.1) vektor \(b-Ax\) okomit na njega. Kako za svaka dva okomita vektora \(u\) i \(v\) vrijedi Pitagorin identitet jer
dobivamo
Nejednakost je stroga jer se jednakost može postići tek ako je \(A(\hat x - x) = 0\), što je moguće samo ako je \(\hat x = x\) jer je \(A\) punog ranga.
Korak 2. Ponovno promatramo \(x \in \R^m\) sa svojstvom (4.1) (bez dokaza postoji li). U ovom koraku dokažimo da \(x\) ima to svojstvo ako i samo ako je rješenje sustava \(A^TA x = A^T b\).
Svojstvo (4.1), odnosno da je za neki \(x\) vektor \(b-Ax\) okomit na elemente slike od \(A\), ekvivalentno je s time da za svaki \(\hat x \in \R^{m}\) vrijedi
Ako vrijedi gornja jednakost za svaki \(\hat x \in \R^m\), pa tako i za \(\hat x=A^TAx-A^Tb\), odakle slijedi
Obratno, ako je \(A^TAx-A^Tb=0\), tada jasno vrijedi \(\langle A^TAx-A^Tb, \hat x\rangle = \langle 0, \hat x \rangle = 0\) za sve \(\hat x \in \R^m\). Time smo dokazali da je svojstvo (4.1) ekvivalentno sa
odnosno s time da je \(x\) rješenje sustava \(A^TAx=A^Tb\).
Korak 3. Dokažimo da sustav normalnih jednadžbi \(A^TAx=A^Tb\) ima jedinstveno rješenje. Za to je potrebno dokazati da je matrica \(A^TA \in \R^{m \times m}\) regularna, odnosno da joj je rang jednak \(m\).
Dokazat ćemo da vrijedi \(\mathcal R(A^T A) = \mathcal R (A^T)\). To posebno znači da matrica \(A^TA\) i \(A^T\) imaju isti rang, a to je \(m\), što će dovršiti dokaz ovog koraka.
Neka je \(y \in \mathcal R (A^TA)\). Dakle, postoji \(z \in \R^m\) takav da je \(y = A^TAz\). No tada je \(y = A^T (Az)\), što dokazuje da je \(y\in \mathcal R(A^T)\).
Neka je \(y \in \mathcal R (A^T)\). Dakle, postoji \(z \in \R^n\) takav da je \(y = A^Tz\). Kako je \(\R^n = \mathcal R (A) \oplus \mathcal N (A^T)\), \(z\) možemo pisati kao \(z=Aw_1+w_2\), gdje je \(w_2 \in \mathcal N(A^T)\). Sada imamo
što dokazuje da je \(y\in \mathcal R (A^TA)\).
Korak 4. Zaključimo dokaz počevši s kraja. Sustav normalnih jednadžbi (prema Koraku 3) ima jedinstveno rješenje. To rješenje, prema Koraku 2, zadovoljava svojstvo (4.1), što prema Koraku 1 znači da je rješenje problema najmanjih kvadrata. Problem najmanjih kvadrata ima jedinstveno rješenje, ponovno prema Koraku 1.
Ovaj teorem daje nam teorijsku egzistenciju i jedinstvenost rješenja, te karakterizaciju tog rješenja preko sustava normalnih jednadžbi. Ipak, u praksi se rijetko koristi sustav normalnih jednadžbi budući da može svesti loše uvjetovan problem na katastrofalno uvjetovan problem. Kao primjer uzmimo \(A = \begin{bmatrix} \varepsilon & 0 \\ 0 & 1 \end{bmatrix}\). Uvjetovanost ove matrice je \(\varepsilon^{-1}\), dok je uvjetovanost matrice \(A^TA\) jednaka \(\varepsilon^{-2}\). Ako je \(\varepsilon\) malen, sustav normalnih jednadžbi može imati mnogo lošiju uvjetovanost od originalne matrice \(A\), te nepotrebno dodatno pokvariti točnost rješenja.
Promotrimo ponovno Primjer 4.1. U tom slučaju zapravo smo imali
Sustav normalnih jednadžbi je tada dan s
što je isti sustav koji smo i rješavali da bismo odredili koeficijente \(a\) i \(b\).
S druge strane, u tom smo primjeru do sustava za \(a\) i \(b\) došli argumentima diferencijalnog računa više varijabli. To možemo i u generalnom slučaju. Promotrimo preslikavanje \(S : \R^m \to \R\),
To je preslikavanje glatko, za prve i druge derivacije vrijedi
Može se pokazati da je matrica drugih derivacija pozitivno definitna, pa je funkcija \(S\) konveksna, a njezina stacionarna točka (nultočka jednadžbe \(\nabla S (x) = 0\)) jedina točka globalnog minimuma. Uz preciznije opravdanje svih koraka, to je alternativni dokaz Teorema 4.3. Analiza može biti i kraća, funkcija \(S\) je kvadratna funkcija po \(x\), pa lokalni minimum možemo naći slično kao tjeme kvadratne funkcije u jednoj varijabli.