Ctrl+K

Obične diferencijalne jednadžbe

Hide code cell source 
import matplotlib.pyplot as plt;
import math;
import numpy as np
import math
from scipy.integrate import RK45

5.3. Obične diferencijalne jednadžbe#

U ovom poglavlju bavit ćemo se temom kojom se možda još niste susreli na drugim kolegijima. Riječ je o običnim diferencijalnim jednadžbama, jednadžbama u kojima je nepoznanica funkcija dana jednadžbom koja uključuje i njene derivacije.

Definicija 5.25 (Obična diferencijalna jednadžba)

Obična diferencijalna jednadžba prvog reda u eksplicitnom obliku je jednadžba oblika

\[y' = f(x,y).\]

Ovdje je \(f\) poznata funkcija dviju varijabli, a \(y\) nepoznata funkcija koju treba odrediti.

Ova jednadžba je eksplicitna jer je derivacija nepoznate funkcije dana eksplicitno u ovisnosti o ostalim podatcima (vrijednostima funkcije \(y\) i varijabli \(x\)). Prvog je reda jer se pojavljuje samo prva derivacija.

Neki primjeri diferencijalnih jednadžbi:

  • \(y' = y\),

  • \(y' = y(1-y)\),

  • \(y' = x^2 + \sin x e^y\).

Notacija

Uobičajena notacija \(y' = f(x, y)\) se može činiti neobičnom na prvi pogled. Nepoznata funkcija \(y\) ovisi o varijabli \(x\), pa zapravo jednadžba glasi:

\[ y'(x) = f(x, y(x)), \quad \text{za sve } x \in I. \]

Kod nas će tipično biti \(I = [x_0, X]\) za neke zadane brojeve \(x_0\) i \(X\).

Tako gornji primjeri zapravo glase:

\[\begin{split} \begin{array}{lcl} y'(x) = y(x) &\leadsto& f(x, y) = y, \\ y'(x) = y(x)(1-y(x)) &\leadsto& f(x, y) = y(1-y), \\ y'(x) = x^2 + \sin x e^{y(x)} &\leadsto& f(x, y) = x^2 + \sin x e^y. \end{array} \end{split}\]

Vidimo da je funkcija s desne strane „obična” \(f : \R \times \R \to \R\), tj. kao drugi argument prima realni broj, a ne neku funkciju.

Jedinstvenost rješenja obične diferencijalne jednadžbe postići će se kada jednadžbi dodamo još početni uvjet oblika \(y(x_0) = y_0\). Jednadžba i početni uvjet zajedno

(5.10)#\[\begin{split}\begin{align} & y' = f(x,y), \\ & y(x_0) = y_0 \end{align}\end{split}\]

nazivamo inicijalnom zadaćom (ponekad se kaže i početna zadaća ili Cauchyjev problem).

Egzistenciju rješenja daje teorem u nastavku.

Teorem 5.26 (Picardov teorem)

Neka je \(\Omega \subseteq \R^2\) otvoren skup, \(f:\Omega \to \R\) dana funkcija te \((x_0,y_0) \in \Omega\). Neka su \(\Delta, \eta > 0\) takvi da je zatvarač pravokutnika \(\bar{P}\),

\[P = (x_0 − \Delta, x_0 + \Delta) \times (y_0 − \eta, y_0 + \eta)\]

sadržan u otvorenom skupu \(\Omega\) i neka je \(f\) neprekidna na \(\bar{P}\) te Lipschitz-neprekidna po drugoj varijabli na \(\bar{P}\). Tada postoji \(\delta \in \langle 0, \Delta]\) tako da inicijalna zadaća (5.10) ima jedinstveno rješenje na intervalu \(I_\delta = (x_0 − \delta, x_0 + \delta)\).

Definicija 5.27 (Lipschitz-neprekidnost)

Kažemo da je \(f : \Omega \to \R\) Lipschitz-neprekidna po drugoj varijabli na skupu \(S \subseteq Ω\) ako postoji \(L\geq 0\) (neovisan o \((x,y) \in \Omega)\) takav da vrijedi

\[|f(x, y_1) − f(x, y_2)| \leq L|y_1 − y_2|,\]

za sve \((x, y_1), (x, y_2) \in S\).

Lipschitz-neprekidnost definira se jednostavnije za funkcije jedne varijable. Napomenimo da je pojam Lipschitz-neprekidnost „jači” od obične neprekidnosti, ali slabiji od derivabilnosti.

U nastavku se nećemo baviti ovim teoremom, nego nadalje za potrebe kolegija pretpostavljamo da zadaće kojima ćemo se baviti zadovoljavaju uvjete Picardovog teorema, pa stoga i imaju rješenje.

Obične diferencijalne jednadžbe generaliziraju problem nalaženja određenog integrala: svaki integral \(\displaystyle \int_a^b f(x) dx\) možemo zapisati kao običnu diferencijalnu jednadžbu \(y' = f(x)\), u kojoj je funkcija \(f\) s desne strane jednostavnog oblika (ovisi samo o \(x\), a ne i o \(y\)). Dodamo li početni uvjet \(y(a)=0\), određeni integral zapravo je vrijednost \(y(b)\). Ovo navodimo da dobijemo intuiciju kako je s analitičke strane problem rješavanja obične diferencijalne jednadžbe još teži nego problem određivanja integrala, za koji isto često moramo koristiti numerički pristup. To nas motivira da nađemo numeričke metode rješavanja inicijalnih zadaća.

Opis problema

Na intervalu \([x_0,X]\) i odgovarajuću subdiviziju intervala \(x_i = x_0 + ih\), \(h:= \dfrac{X-x_0}{n}\), \(i=0,1,\dots,n\) potrebno je pronaći vrijednosti \(y_0,y_1,\dots,y_n\) takve da je \(y_i \approx y(x_i)\), gdje je \(y\) rješenje inicijalne zadaće oblika (5.10).

U nastavku \(y(x_i)\) označava vrijednost točnog rješenja funkcije \(y\) u točki \((x_i)\), a \(y_i\) označava aproksimaciju tog rješenja dobivenu numeričkom metodom.

Pogledajmo ponovno jednadžbu \(y' = f(x,y)\), te ju integrirajmo sa svake strane od \(x_i\) do \(x_{i+1}\). Dobivamo

\[y_{i+1} - y_i \approx y(x_{i+1}) - y(x_i) = \int_{x_i}^{x_{i+1}} y' dx = \int_{x_i}^{x_{i+1}} f(x,y(x)) dx.\]

Problem određivanja brojeva \(y_i\) možemo riješiti rekurzivno (\(y_{i+1}\) odredimo koristeći poznatu vrijednost \(y_i\)) ako znamo riješiti integral s desne strane, koji opet ovisi o nepoznatoj funkciji \(y\). Postoje tri standardna načina kako aproksimirati taj integral:

  • koristeći vrijednost u lijevom rubu: \(\displaystyle \int_{x_i}^{x_{i+1}} f(x,y(x)) dx \approx h f(x_i,y_i)\);

  • koristeći vrijednost u desnom rubu: \(\displaystyle \int_{x_i}^{x_{i+1}} f(x,y(x)) dx \approx h f(x_{i+1},y_{i+1})\);

  • koristeći trapeznu formulu: \(\displaystyle \int_{x_i}^{x_{i+1}} f(x,y(x)) dx \approx \frac h2 f(x_{i},y_{i}) + \frac h2 f(x_{i+1},y_{i+1})\).

Za svaki od tih načina dobivamo jednu metodu.

Definicija 5.28

Metodu za rješavanje inicijalne zadaće (5.10) kojom rekurzivno dobivamo vrijednosti \(y_0,y_1,\dots,y_n\),

\[y_0 := y(x_0), \quad y_{i+1} := y_i + hf(x_i,y_i)\]

nazivamo eksplicitnom Eulerovom metodom.

Metodu kojom dobivamo niz

\[y_0 := y(x_0), \quad y_{i+1} := y_i + hf(x_{i+1},y_{i+1})\]

nazivamo implicitnom Eulerovom metodom.

Metodu kojom dobivamo niz

\[y_0 := y(x_0), \quad y_{i+1} := y_i + \frac h2 f(x_{i},y_{i}) + \frac h2 f(x_{i+1},y_{i+1})\]

nazivamo trapeznom metodom, ili Crank-Nicolsonovom metodom.

Eksplicitna Eulerova metoda (zvana ponekad samo Eulerova metoda) najjednostavnija je metoda. Eksplicitna je jer se član \(y_{i+1}\) ne nalazi na desnoj strani, pa je svaki sljedeći član jednostavno izračunati. Druge dvije metode spadaju u implicitne metode, te ovisno o funkciji \(f\) ne mora biti jednostavno izračunati sljedeći član \(y_{i+1}\) (dapače, ponekad to može voditi na nelinearnu jednadžbu koju se može riješiti samo numerički). Uzmemo li u obzir koje smo aproksimacije za integrale uzimali na desnoj strani jednakosti, možemo očekivati da će trapezna metoda dati najbolje rezultate. Provjerimo to primjerom.

Primjer 5.29

Inicijalna zadaća

\[\begin{split}\begin{align} & y' = y, \\ & y(0) = 1 \end{align}\end{split}\]

jedan je od najjednostavnijih primjera običnih diferencijalnih jednadžbi, kojoj je rješenje \(e^x\) (općenito za \(y'=ay\) rješenje je oblika \(C\cdot e^{a x}\), \(C \in \R\)). Spada u linearne jednadžbe koje su rješive analitčki. Primijenimo naučene metode na ovom primjeru tako da nađemo vrijednost \(y(1) = e\).

Kako je \(f(x,y) = y\), eksplicitna Eulerova metoda glasi

\[y_{i+1} = y_i + h y_i \implies y_{i+1} = (1+h) y_i,\]

odnosno

\[y_{i} = (1+h)^{i} \cdot y_0 = (1+h)^{i}.\]

Uzmemo li \(i\) tako da je \(ih = 1\), aproksimacija za \(y(1)\) glasi \((1+h)^{1/h}\), što zaista teži u \(e\) kada \(h\to 0\). Dakle, kako se \(h\) smanjuje, očekivano dobivamo sve bolji rezultat.

Za implicitnu metodu imamo

\[y_{i+1} = y_i + h y_{i+1} \implies (1-h)y_{i+1} = y_i,\]

odnosno

\[y_{i} = (1-h)^{-i}.\]

Ponovno i aproksimacija \((1-h)^{-1/h}\) teži k \(e\) kad \(h \to 0\).

Za trapeznu metodu imamo

\[y_{i+1} = y_i + \dfrac h2 y_{i} + \dfrac h2 y_{i+1} \implies \left(1-\dfrac h2 \right)y_{i+1} = \left(1+\dfrac h2 \right)y_i,\]

odnosno

\[y_{i} = \left( \dfrac{1+\frac h2 }{1-\frac h2 }\right)^{i},\]

te se slično može vidjeti konvergencija prema točnom rješenju i ovom metodom.

Promotrimo grafove stvarnih apsolutnih grešaka za ove metode u ovisnosti o parametru \(h\), u Pythonu.

Hide code cell source 
def PrimjerODJ (h_ovi, metoda = 0):
    # Prima polje različitih vrijednosti od h i varijablu "metoda" kojom biramo metodu:
    # - eksplicitni Euler (ako metoda = 0).
    # - implicitni Euler (ako metoda = 1).
    # - trapezna metoda (ako metoda = 2).
    # Za svaki h, određuje se apsolutna greška prilikom aproksimacije u y(1),
    # y'=y, y(0)=1 odabranom metodom za taj h.
    # Funkcija vraća polje dobivenih grešaka.
    N = len(h_ovi)
    greske = [0] * N
    prava_vrijednost = math.exp(1)
    for i in range(N):
        h = h_ovi[i]
        if metoda == 0:
            # eksplicitni Euler
            aprox_vrijednost = (1+h) ** (1/h)
        elif metoda == 1:
            # implicitni Euler
            aprox_vrijednost = (1-h) ** (-1/h)
        else:
            # trapezna formula
            aprox_vrijednost = ((1+h/2)/(1-h/2)) ** (1/h)
        greske[i] = abs(aprox_vrijednost - prava_vrijednost)
    return greske

h_ovi = [2 ** (-broj) for broj in range(1, 14)]
greske_explEuler = PrimjerODJ(h_ovi, 0)
greske_implEuler = PrimjerODJ(h_ovi, 1)
greske_trapez = PrimjerODJ(h_ovi, 2)

fig = plt.figure(figsize=[16, 5])
ax1 = fig.add_subplot(121)
ax1.title.set_text(f'Graf greške ODJ metoda')
ax1.plot(h_ovi, greske_explEuler,  marker='o', color='b', label='eksplicitni Euler')
ax1.plot(h_ovi, greske_implEuler,  marker='o', color='r', label='implicitni Euler')
ax1.plot(h_ovi, greske_trapez,  marker='o', color='g', label='trapezna formula')
plt.xlabel( 'h' )
plt.ylabel( 'greška E(h)' )
plt.legend()
ax1 = fig.add_subplot(122)
ax1.title.set_text(f'Log-log graf greške ODJ metoda')
plt.loglog(h_ovi, greske_explEuler,  marker='o', color='b', label='eksplicitni Euler')
plt.loglog(h_ovi, greske_implEuler,  marker='o', color='r', label='implicitni Euler')
plt.loglog(h_ovi, greske_trapez,  marker='o', color='g', label='trapezna formula')
plt.xlabel( 'h' )
plt.ylabel( 'greška E(h)' )
plt.legend()
plt.show()
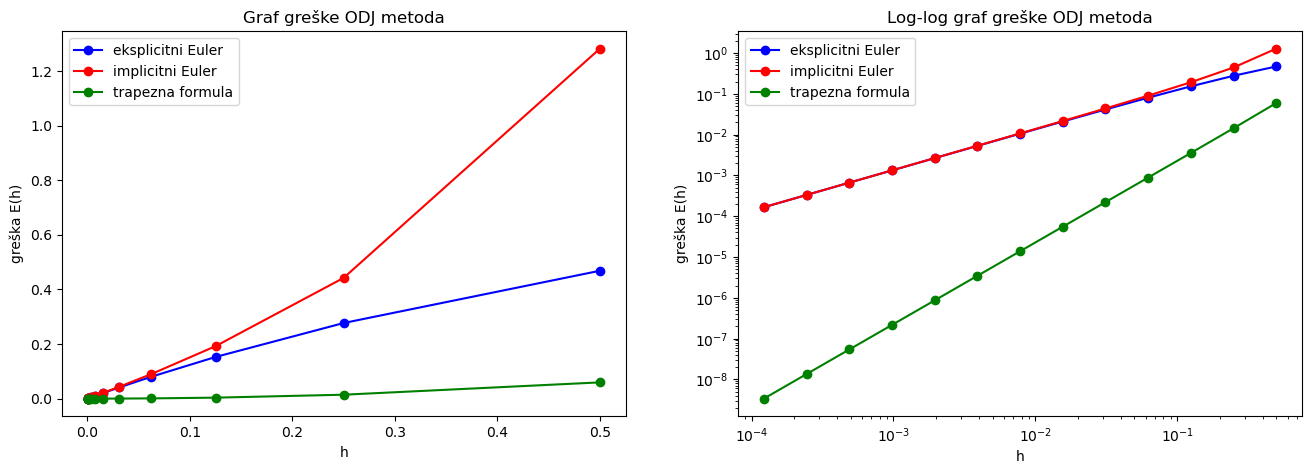
_images/0eba4f0a4cf656c3632335d5713b1505c1a1671b9c38388b86f38df8c12bc5f8.png

Vidimo da se trapezna metoda ponaša mnogo bolje od drugih dviju metoda. Čini se da trapezna formula ima red konvergencije jednak \(2\), a Eulerove metode red konvergencije \(1\). Takav sličan zaključak će nam reći i kasnija analiza.

Primjer 5.30

Jednadžba

\[y' = y(1-y)\]

naziva se logistička jednadžba, te je jedna od jednostavnijih i najraširenijih nelinearnih običnih diferencijalnih. Njena rješenja su oblika

\[y'(x) = \dfrac{1}{1+Ce^{-x}}\]

(za neki \(C \in \R\)). Pogledajmo primjenu implicitne Eulerove metode za ovu jednadžbu. Član \(y_{i+1}\) računamo iz formule

\[y_{i+1} = y_i + hy_{i+1}(1-y_{i+1}) \implies hy^2_{i+1} + (1-h)y_{i+1} - y_i = 0.\]

Već u slučaju jedne od najjednostavnijih nelinearnih jednadžbi dolazimo do malog problema. Dobili smo kvadratnu jednadžbu po \(y_{i+1}\) koju možemo eksplicitno riješiti, ali za koju moramo znati koje od dvaju rješenja treba uzeti. Problem je moguće riješiti, ali ovaj primjer služi da pokažemo kako se implicitna Eulerova metoda (a slično je i s trapeznom) vrlo brzo može zakomplicirati.

Jednokoračne metode#

Sve navedene metode spadaju u kategoriju jednokoračnih metoda.

Definicija 5.31

Metodu za rješavanje inicijalne zadaće (5.10) kojom rekurzivno dobivamo vrijednosti \(y_0,y_1,\dots,y_n\),

\[y_0 := y(x_0), \quad y_{i+1} := y_i + h\Phi_h(x_i,y_i),\]

gdje je \(\Phi\) neprekidna funkcija u varijablama \(x_i\), \(y_i\) i \(h\), nazivamo jednokoračnom metodom.

Cilj nam je naći rezultat koji će za sve jednokoračne metode pokazati da kako \(h\to 0\) da aproksimacije \(y_i\) teže ka \(y(x_i)\).

Definicija 5.32

Globalna pogreška diskretizacije za \(x_i\) definira se kao

\[\gamma_i := y_{i} - y(x_i).\]

Kažemo da je metoda reda konvergencije \(p\) ako postoji konstanta \(C>0\) takva da je

\[\max_{i=0,\dots,n} |\gamma_i| \leq Ch^p.\]

Pogledajmo ponovno Primjer 5.29 za eksplicitnu Eulerovu metodu, za \(h=2^{-3}\) i greške koje dobivamo za točke diskretizacije:

Hide code cell source 
h= 2**(-3)
tocniy = [math.exp(h*i) for i in range(0,9)]
approxy = [(1+h) ** i for i in range(0,9)]
print(f'   y(xi) \t     yi \t  |gammai|')
print(f'----------- \t ----------- \t -----------')
for i in range(0,9):
    print(f'{tocniy[i]:.5e} \t {approxy[i]:.5e} \t {abs(tocniy[i] - approxy[i]):.5e}')

   y(xi) 	     yi 	  |gammai|
----------- 	 ----------- 	 -----------
1.00000e+00 	 1.00000e+00 	 0.00000e+00
1.13315e+00 	 1.12500e+00 	 8.14845e-03
1.28403e+00 	 1.26562e+00 	 1.84004e-02
1.45499e+00 	 1.42383e+00 	 3.11633e-02
1.64872e+00 	 1.60181e+00 	 4.69146e-02
1.86825e+00 	 1.80203e+00 	 6.62135e-02
2.11700e+00 	 2.02729e+00 	 8.97135e-02
2.39888e+00 	 2.28070e+00 	 1.18178e-01
2.71828e+00 	 2.56578e+00 	 1.52497e-01

Iz tablice vidimo da kako raste \(i\), tako sve više raste greška koju činimo. Razlog leži u tome što svakom koraku zapravo radimo dvije greške. Pored činjenice da griješimo svaki put kad aproksimiramo integral \(\displaystyle \int_{x_i}^{x_{i+1}} f(x,y(x)) dx\), grešku radimo i time što se u argumentu funkcije \(f\) ne nalazi prava vrijednost \(y(x)\) nego naše aproksimacije \(y_i\) i \(y_{i+1}\), koje su već donijele neku grešku. To je zajedničko svim navedenim metodama, te će to biti i ključno za rezultat ocjene pogreške.

Definicija 5.33

Lokalna pogreška diskretizacije za \(x\), i \(h\) definira se kao

\[\epsilon (x,h) := y(x+h) - y(x) - h \Phi_h (x,y(x)).\]

Kažemo da je metoda reda konzistentnosti \(p\) ako postoji konstanta \(C>0\) takva da je

\[\max_{x \in [x_0,X]} |\epsilon(x,h)| \leq Ch^{p+1}.\]

Lokalna pogreška diskretizacije mjeri koju bismo grešku učinili da integral \(\displaystyle \int_{x_i}^{x_{i+1}} f(x,y(x)) dx\) računamo s pravim vrijednostima \(y(x_i), y(x_{i+1})\), a ne trenutnim aproksimacijama \(y_i, y_{i+1}\).

Također, primijetimo da iz definicije lokalne pogreške diskretizacije dobivamo

\[\frac{\epsilon (x,h)}{h} = \frac{y(x+h) - y(x)}{h} - \Phi_h (x,y).\]

Kako kvocijent na lijevoj strani teži k \(f'(x,y) = y'(x)\), a metoda ima smisla tek ako obje strane teže k nuli, dobivamo sljedeću definiciju.

Definicija 5.34

Jednokoračna metoda je konzistentna ako za svaki \(x \in [x_0,X]\) vrijedi

\[\lim_{h\to 0} \Phi_h(x,y) = f(x,y(x)).\]

Konačno možemo dokazati sljedeći rezultat.

Teorem 5.35

Neka je jednokoračna metoda dana funkcijom \(\Phi_h\) koja je Lipschitz-neprekidna u drugoj varijabli: postoji konstanta \(L_\Phi >0\) takva da za sve \(x \in [x_0,X]\), \(h>0\) i \(y_1, y_2 \in \R\) vrijedi

\[\left| \Phi_h(x,y_1) - \Phi_h(x,y_2) \right| \leq L_\phi |y_1 - y_2|.\]

Tada vrijedi

\[\max_{i=0,\dots,n} |\gamma_i| \leq \frac{1}{hL_\Phi} \left( e^{L_\phi (X-x_0)} -1 \right) \max_{i=0,\dots,n} |\epsilon (x_i,h)|.\]

Ako je metoda reda konzistentnosti \(p\geq 1\), tada je i reda konvergencije \(p\).

Dokaz.

Oduzmimo definiciju metode

\[y_{i+1} = y_i + h\Phi_h(x_i,y_i)\]

i definiciju lokalne pogreške diskretizacije

\[y(x_{i+1}) - y(x_i) - h \Phi_h (x_i,y(x_i)) = \epsilon(x_i,h)\]

u točki \(x_i\). Dobivamo

\[\gamma_{i+1} = \gamma_i + h \left( \Phi_h(x_i,y_i) - \Phi_h(x_i,y(x_i))\right) - \epsilon(x_i,h).\]

Koristeći pretpostavku o funkciji \(\Phi_h\) i nejednakost trokuta, dobivamo

\[\begin{split}\begin{align*} |\gamma_{i+1}| &\leq |\gamma_i| + h\left| \Phi_h(x_i,y_i) - \Phi_h(x_i,y(x_i))\right| + h |\epsilon(x_i,h)|\\ &\leq |\gamma_i| + h L_\Phi | \gamma_i | + |\epsilon(x_i,h)| \\ &\leq (1+ h L_\Phi) | \gamma_i | + \max_{i=0,\dots,n} |\epsilon (x_i,h)|. \end{align*}\end{split}\]

Dobili smo niz nejednakosti oblika

\[z_{i+1} \leq (1+Ah) z_i + Bh\]

gdje je

\[z_i := |\gamma_i|, \quad A:= L_\Phi, \quad B:=\max_{i=0,\dots,n} \frac{1}{h} |\epsilon (x_i,h)|.\]

Kako je dodatno \(z_0 =0\), indukcijom se pokaže da svaki takav niz vrijedi

\[z_i \leq \frac{B}{A} \left( (1+Ah)^i - 1 \right).\]

Iskoristimo ovu nejednakost za \(i=n\), iskoristimo nejednakost \(e^t \geq 1+t\) (za \(t>0\)), te vratimo supstitucije. Dobivamo

\[|\gamma_{n}| \leq \frac{1}{hL_\Phi} \left( e^{L_\Phi(X-x_0)} - 1 \right) \max_{i=0,\dots,n} |\epsilon (x_i,h)|,\]

što je i trebalo dokazati.

Sada možemo dokazati konvergenciju svih spomenutih metoda. U dokazu ćemo koristiti veću glatkoću nepoznate funkcije \(y\) koja se može dokazati u slučaju da je funkcija \(f\) iz diferencijalne jednadžbe dovoljno glatka. Taj korak za potrebe ovog kolegija preskačemo, nego u sljedećim rezultatima pretpostavljamo dovoljnu glatkoću rješenja \(y\).

Propozicija 5.36

Pretpostavimo da je funkcija \(f\) iz zadaće (5.10) Lipschitz-neprekidna, te da je funkcija \(y\) klase \(C^2([x_0,X]).\) Tada za eksplicitnu Eulerovu metodu vrijedi

\[|\epsilon (x,h)| \leq \frac{h^2}{2} M_2,\]

gdje je \(M_{n+1} := \max_{x \in [x_0, X]} |y^{(n+1)}(x)|\). Metoda konvergira te joj je red konvergencije jednak \(1\).

Dokaz.

Neka je \(L\) konstanta Lipschitz-neprekidnosti za funkciju \(f\). Za funkciju \(\Phi_h\) vrijedi

\[\Phi_h (x,y) = f(x,y),\]

pa je funkcija \(\Phi_h\) Lipschitz-neprekidna po drugoj varijabli s konstantom \(L_\Phi = L\).

Kako je \(y\) dvaput derivabilna, iz Taylorovog teorema postoji \(\xi \in \langle x, x+h \rangle \subseteq [x_0,X]\) takav da

\[\begin{split}\begin{align*} y(x + h) &= y(x) + h y'(x) + \frac{h^2}{2}y''(\xi) \\ &= y(x) + h f(x,y) + \frac{h^2}{2}y''(\xi) \\ &= y(x) + h \Phi_h (x,y) + \frac{h^2}{2}y''(\xi). \end{align*}\end{split}\]

Kako je dodatno \(y\) klase \(C^2\), slijedi

\[|\epsilon(x,h)| = \left| \frac{h^2}{2} y''(\xi) \right| \leq \frac{h^2}{2} M_2.\]

Preostale tvrdnje slijede primjenom Teorema 5.35.

Propozicija 5.37

Pretpostavimo da je funkcija \(f\) iz zadaće (5.10) Lipschitz-neprekidna, te da je funkcija \(y\) klase \(C^3([x_0,X]).\) Tada za trapeznu metodu (uz dovoljno mali \(h\)) vrijedi

\[|\epsilon (x,h)| \leq \frac{h^3}{6} M_3.\]

Metoda konvergira te joj je red konvergencije jednak \(2\).

Dokaz.

Neka je \(L\) konstanta Lipschitz-neprekidnosti za funkciju \(f\). Iz definicije metode i funkcije \(\Phi_h\) dobivamo

\[y_i + h \Phi_h (x_i,y_i) = y_{i+1} = y_i + \dfrac h2 f(x_{i},y_{i}) + \dfrac h2 f(x_{i+1},y_{i+1}).\]

Izjednačavanjem prvog i zadnjeg izraza, dobivamo

\[\begin{split}\begin{align*} h \Phi_h (x_i,y_i) &= \dfrac h2 f(x_{i},y_{i}) + \dfrac h2 f(x_{i+1},y_{i+1}) \\ &= \dfrac h2 f(x_i , y_i ) + \dfrac h2 f(x_i+h , y_i + h \Phi_h (x_i,y_i)), \end{align*}\end{split}\]

odakle čitamo implicitnu definiciju funkcije \(\Phi_h\) preko funkcije \(f\):

\[\Phi_h (x,y) = \dfrac 12 f(x , y ) + \dfrac 12 f(x+h , y + h \Phi_h (x,y)).\]

Svejedno možemo odrediti konstantu Lipschitz-neprekidnosti: za neke \(x\in [x_0,X]\), \(y_1, y_2 \in \R\) vrijedi

\[\begin{split}\begin{align*} \left| \Phi_h (x,y_1) - \Phi_h (x,y_2) \right| &= \left| \dfrac 12 f(x , y_1 ) + \dfrac 12 f(x+h , y_1 + h \Phi_h (x,y_1)) - \dfrac 12 f(x , y_2 ) - \dfrac 12 f(x+h , y_2 + h \Phi_h (x,y_2)) \right| \\ & \leq \dfrac 12 L |y_1 - y_2| + \dfrac 12 L \left| (y_1 + h \Phi_h (x,y_1)) - ( y_2 + h \Phi_h (x,y_2)) \right| \\ & \leq \dfrac 12 L |y_1 - y_2| + \dfrac 12 L \left| y_1 - y_2 \right| + \dfrac 12 hL \left| \Phi_h (x,y_1) - \Phi_h (x,y_2) \right|. \end{align*}\end{split}\]

S lijeve i zdesne strane dobili smo isti izraz. Zato, kada je \(hL<2\), vrijedi

\[\left| \Phi_h (x,y_1) - \Phi_h (x,y_2) \right| \leq \frac{2L}{2-hL} \left| y_1 - y_2 \right|,\]

odakle zaključujemo da je \(\Phi_h\) Lipschitz-neprekidna po drugoj varijabli uz konstantu \(L_\Phi := \dfrac{2L}{2-hL} \) .

Ocijenimo sada lokalnu grešku diskretizacije (na nekim mjestima pišemo \(y\) umjesto \(y(x)\) radi preglednosti):

\[\begin{split}\begin{align*} \epsilon (x,h) &= y (x+h) - y(x) - h \Phi_h(x, y(x)) \\ &= y (x+h) - y(x) - \dfrac h2 f(x, y) - \dfrac h2 f(x + h, y + h \Phi_h(x, y)) \\ &= y (x+h) - y(x) - \dfrac h2 f(x, y) - \dfrac h2 f(x+h, y(x+h)) + \dfrac h2 f(x+h, y(x+h)) - \dfrac h2 f(x + h, y + h \Phi_h(x, y)) \\ &= y (x+h) - y(x) - \dfrac h2 y'(x) - \dfrac h2 y'(x+h) + \dfrac h2 (f(x+h, y(x+h)) - f(x + h, y + h \Phi_h(x, y)) ). \end{align*}\end{split}\]

Grešku ćemo odrediti tako da primijenimo trapeznu formulu za integral \(\displaystyle \int_x^{x+h} y'(t) dt\) i odgovarajuću ocjenu greške. Naime, prema trapeznoj formuli vrijedi

\[y(x+h) - y(x) = \displaystyle \int_x^{x+h} y'(t) dt \approx \dfrac h2 y'(x) + \dfrac h2 y'(x+h).\]

Razlika izraza slijeva i zdesna je jednaka grešci trapezne formule za taj integral. Koristeći da je \(y\) klase \(C^3\) i ocjenu iz Teorema 5.14, dobivamo

\[\begin{split}\begin{align*} |\epsilon (x,h)| & \leq \frac{h^3}{12} M_3 + \dfrac h2 |f(x+h, y(x+h)) - f(x + h, y(x) + h \Phi_h(x, y(x)))| \\ & \leq \frac{h^3}{12} M_3 + \dfrac {hL}2 |y(x+h) - y(x) - h \Phi_h(x, y(x))| \\ &= \frac{h^3}{12} M_3 + \dfrac {hL}2 |\epsilon(x, h)|, \end{align*}\end{split}\]

gdje smo za zadnju nejednakost primijenili Lipschitzovo svojstvo funkcije \(f\). Iz gornje nejednakosti imamo

\[ |\epsilon (x,h)| \leq \frac{1}{1-hL/2} \frac{h^3}{12} M_3 \leq \frac{h^3}{6} M_3, \]

kada je \(\frac{1}{1-hL/2} \leq 2\), odnosno, \(hL \leq 1\). Sada tvrdnju teorema dobijemo jednostavno uvrštavanjem u Teorem 5.35.

Runge-Kuttina metoda#

Za kraj objasnit ćemo još jednu metodu koja je popularna među inženjerima budući da je eksplicitna, a visokog je reda. Jedina eksplicitna metoda koju do sada poznajemo je eksplicitna Eulerova, kod koje je \(\Phi_h(x,y) = f(x,y)\). Dakle, inkrement kojim računamo sljedeću vrijednost \(y_{i+1}\) ovisi samo o evaluaciji funkcije \(f\) u jednoj točki domene \(x\) i jednoj (prošloj) aproksimaciji nepoznate funkcije \(y\). To možemo popraviti tako da funkciju \(\Phi_h\) računamo iz više evaluacija funkcije \(f\) u nadi da će se time bolje aproksimirati \(\displaystyle \int_{x_i}^{x_{i+1}} f(x,y(x))dx\).

Za neki \(m\in \mathbb N\) tražimo neke konstante \(a_{2,1},a_{3,1},a_{3,2}, a_{4,1} \dots, a_{m,m-1}\), \(b_1, \dots, b_n\) i \(c_2,\dots,c_n\) takve da s funkcijom

\[\Phi_h (x,y) = \sum_{i=1}^m b_i k_i, \quad k_i := f\left(x + c_ih, y + h \sum_{j=1}^{i-1} a_{i,j} k_j \right)\]

imamo što bolji red konvergencije. Brojeve \(k_i\), budući da su izračunati kao vrijednosti funkcije \(f\) u nekim točkama blizu originalne \((x,y)\), možemo smatrati aproksimacijom inkrementa za \(y\). Postoje prirodni uvjeti koji su logični ili koji se lako provjere: \(c_1=0\), suma svih \(b_i\) je jednaka \(1\), sve navedene konstante su iz intervala \([0,1]\). Ostali uvjeti provjeravaju se tako da se za fiksne i male \(m\) promatra Taylorov razvoj te se promatra koje jednadžbe moraju biti zadovoljene da bi se postigla što bolja greška. Metode koje su proizašle iz ovakve analize nazivaju se Runge-Kuttine metode. Najraširenija je jedna od onih kod koje je \(m=4\).

Definicija 5.38

Metodu za rješavanje inicijalne zadaće (5.10) kod koje je te kojom rekurzivno dobivamo vrijednosti \(y_0,y_1,\dots,y_n\),

\[y_0 := y(x_0), \quad y_{i+1} := y_i + \frac{h}{6}\left(k_1+2k_2+2k_3+k_4 \right),\]

pri čemu je

\[\begin{split}\begin{align*} k_1 &= f\left(x_i,y_i\right),\\ k_2 &= f\left(x_i+\frac{h}{2},y_i+\frac{h}{2}k_1\right),\\ k_3 &= f\left(x_i+\frac{h}{2},y_i+\frac{h}{2}k_2\right),\\ k_4 &= f\left(x_i+h,y_i+hk_3\right), \end{align*}\end{split}\]

nazivamo klasičnom Runge-Kuttinom metodom.

Kao i sve Runge-Kuttine metode, ova metoda je eksplicitna. Za ovu metodu red konvergencije je jednak \(4\).

Primjer poziva u Pythonu, za inicijalnu zadaću \(y'(x)=y, y(0)=1\) klasičnom Runge-Kuttinom metodom:

Hide code cell source 
def f(t, u):
  return u

t0 = 0
N = 10
u0 = np.array([1])
t_max = 1.0
dt = t_max/N

# Metoda RK45 iz scipy.integrate. 
# To je zapravo varijanta metode RK4 opisane gore u skripti.
# Donja naredba samo stvara objekt tipa RK45 
# (tj. poziva konstruktor i još ne rješava ODJ).
solution = RK45(f, t0, u0, t_max, dt, first_step=dt)

# Egzaktno rješenje jednadžbe u'(t) = u(t) je u(t) = exp(t).
# Evaluiramo ga u točkama t_i = i*dt, za i=0, 1, ..., N.
pravorj = [math.exp(i*dt) for i in range (N+1)]

print(f'  t \t    u(t) \t   greska ')
print(f'----- \t ----------- \t -----------')
print(f'{0:.1f} \t {u0[0]:.5e} \t {abs(pravorj[0]-u0[0]):.5e}')
for i in range(1, N+1):
    # Pomaknemo se sa t_{i-1} na t_i.
    solution.step()

    # Dohvatimo rješenje u t_i.
    u = solution.y[0]
    t = solution.t

    # Ispišemo rješenje i grešku do egz. vrijednosti exp(t_i).
    print(f'{i*dt:.1f} \t {u:.5e}  \t {abs(pravorj[i]-u):.5e}')

  t 	    u(t) 	   greska 
----- 	 ----------- 	 -----------
0.0 	 1.00000e+00 	 0.00000e+00
0.1 	 1.10517e+00  	 2.57686e-10
0.2 	 1.22140e+00  	 5.69573e-10
0.3 	 1.34986e+00  	 9.44214e-10
0.4 	 1.49182e+00  	 1.39136e-09
0.5 	 1.64872e+00  	 1.92211e-09
0.6 	 1.82212e+00  	 2.54911e-09
0.7 	 2.01375e+00  	 3.28674e-09
0.8 	 2.22554e+00  	 4.15132e-09
0.9 	 2.45960e+00  	 5.16141e-09
1.0 	 2.71828e+00  	 6.33805e-09
Sadržaj