Greške približnog računanja i aritmetike računala

Sadržaj

1.3. Greške približnog računanja i aritmetike računala#

Računalo za pohranu brojeva koristi nekoliko različitih tipova podataka. Na primjer, u C-u imamo tipove char, short, int, long za pohranu cijelih, te float i double za pohranu realnih brojeva. Varijable svakih od ovih tipova zauzimaju neku malu količinu memorije (od 8 do 64 bita za navedene) te se stoga u njih može spremiti samo neki mali konačni podskup skupa \(\mathbb{Z}\) ili \(\R\).

U numeričkoj matematici uglavnom radimo s realnim varijablama, pa ćemo se ukratko podsjetiti na zapis realnih brojeva u računalu. Taj zapis će imati direktne posljedice na točnost računanja.

Zapis realnih brojeva u računalu#

Realni brojevi u računalu zapisuju se u binarnom brojevnom sustavu. Standard koji se pritom koristi je IEEE-754. Promotrimo kako to izgleda u slučaju zapisa jednostruke točnosti (32-bitni realni broj, float u C-u).

_images/01c_wiki_float32.png — Slika 1.1 Zapis realnog broja \(x=0.15625\) u 32-bitnoj varijabli; preuzeto s Wikipedie.#

Općenito, ako su u gornjim „kućicama” pohranjene redom binarne znamenke \(b_{31} b_{30} \ldots b_2 b_1 b_0\), onda prvi bit \(b_{31}\) označava predznak („sign”, plavo na slici), idućih \(w=8\) bitova \(b_{30}\ldots b_{23}\) (zeleno na slici) eksponent uvećan za \(2^w-1 = 127\), a zadnjih \(t=23\) bitova \(b_{22}\ldots b_0\) mantisu („fraction”, crveno na slici) i zapisan je broj

\[ \begin{align*} x &= (-1)^{b_{31}} \cdot 2^{(b_{30} b_{29} \ldots b_{23})_2 - 127} \cdot (1.b_{22}b_{21}\ldots b_0)_2. \end{align*} \]

Uvjerite se da bitovi sa slike zaista reprezentiraju broj \(0.15625\).

Standard IEEE-754 dozvoljava različite izbore vrijednosti \(w\) i \(t\) koje predstavljaju duljinu eksponenta (broj zelenih „kućica”) i mantise (broj crvenih „kućica”). Sljedeća tablica prikazuje standardne tipove podataka. Za varijable tipa binary32 kažemo da imaju jednostruku, a varijable tipa binary64 dvostruku točnost. Operacije s ta dva tipa su obično vrlo brze i ugrađene u sve procesore, za razliku od binary128. Obično koristimo binary64 - to je tip double u C-u, a koristi ga i Python za spremanje realnih brojeva.

Ime tipa	`binary32` (`float`)	`binary64` (`double`)	`binary128`
duljina u bitovima	32	64	128
\(t\)	23	52	112
\(w\)	8	11	15
\(u=2^{-(t+1)}\)	\(2^{-24} \approx 5.96 \cdot 10^{-8}\)	\(2^{-53} \approx 1.11 \cdot 10^{-16}\)	\(2^{-113} \approx 9.63 \cdot 10^{-35}\)
raspon brojeva	\(\approx 10^{\pm 38}\)	\(\approx 10^{\pm 308}\)	\(\approx 10^{\pm 4932}\)

Jasno je da u ovakvim varijablama možemo prikazati samo konačno mnogo realnih brojeva: postoji samo \(2^{64}\) različita niza nula i jedinica duljine 64, pa postoji maksimalno toliko različitih realnih brojeva prikazivih u tipu binary64. Najveći prikazivi broj ima maksimalni dozvoljeni eksponent i sve jedinice u mantisi i iznosi \(\approx 10^{308}\), dok najmanji broj veći od nule koji je prikaziv u tom tipu iznosi \(\approx 10^{-308}\).

Greške prilikom spremanja broja u računalu#

Pretpostavimo da realni broj \(x \neq 0\) želimo spremiti u varijablu u računalu. Zapišimo taj broj u bazi 2 i pomaknimo decimalnu (binarnu?) točku tako da samo jedna znamenka 1 bude lijevo od točke:

\[ x = \pm (1.b_{-1} b_{-2} \ldots )_2 \cdot 2^e = \pm \left( 1 + \sum_{i=1}^\infty b_{-i} 2^{-i} \right) \cdot 2^e. \]

Ako u mantisi broja \(x\) ima više od \(t\) znamenki, u računalo će biti spremljena aproksimacija tog broja koja ignorira sve znamenke iza \(b_{-t}\) i koju označavamo sa \(\fl(x)\):

\[ \fl(x) = \pm (1.b_{-1} b_{-2} \ldots \red{b_{-t}})_2 \cdot 2^e = \pm \left( 1 + \sum_{i=1}^\red{t} b_{-i} 2^{-i} \right) \cdot 2^e. \]

Slično kao kod decimalne aritmetike, provodi se i zaokruživanje:

Ako je prva odbačena znamenka \(b_{-(t+1)}=1\), broj zaokružujemo prema gore.
Ako je prva odbačena znamenka \(b_{-(t+1)}=0\), broj zaokružujemo prema dolje.

Na taj način, za apsolutnu grešku spremanja broja \(x\) u računalo vrijedi

\[ |x - \fl(x)| \leq 2^e \cdot 2^{-(t+1)}. \]

Vidimo da apsolutna greška ovisi i o veličini broja \(x\): za \(x\) sa malenim eksponentom \(e\) je greška manja nego za one s velikim \(e\). Zato je prirodnije gledati relativnu grešku: kako je \(|x| \geq 2^e\), imamo

(1.1)#\[ \frac{|x - \fl(x)|}{|x|} \leq \frac{2^e \cdot 2^{-(t+1)}}{2^e} = 2^{-(t+1)} =: u. \]

Relativna greška ne ovisi o veličini broja \(x\) nego samo o tome koliko binarnih znamenki mantise čuvamo.

Definicija 1.8

Ako realne brojeve pohranjujemo u računalu koristeći tip podataka kod kojeg se \(t\) binarnih znamenki koristi za mantisu, a \(w\) za eksponent, onda broj \(u = 2^{-(t+1)}\) zovemo jedinična greška zaokruživanja (engl. unit roundoff).

Dakle, za svaki realni broj \(x\) unutar prikazivog raspona vrijedi da je relativna greška nastala spremanjem \(x\) unutar računala manja od jedinične greške zaokruživanja. U gornjoj tablici su prikazane te greške za standardne tipove podataka; za tip binary64 ona iznosi \(u \approx 1.11 \cdot 10^{-16}\). Stoga je spremanjem u računalu u tip binary64 sačuvano \(\approx 16\) dekadskih znamenki broja \(x\).

Iz (1.1) slijedi da \(\fl(x)\) možemo zapisati i ovako:

\[ \fl(x) = (1 + \varepsilon) x, \quad \text{ za neki } |\varepsilon| \leq u. \]

Ovakav zapis će biti vrlo koristan u nastavku. Uočite (dokažite!) da je ova jednakost upravo ekvivalentna sa (1.1).

Realna aritmetika računala#

Kada u računalu provodimo bilo koju operaciju nad realnim brojevima, konačni rezultat moramo spremiti u varijablu, čime ponovno radimo zaokruživanje kao u prethodnoj cjelini. Standard IEEE-754 propisuje da za 4 osnovne aritmetičke operacije vrijedi:

Dobiveni rezultat spremljen u varijablu mora zadovoljavati istu ocjenu relativne greške zaokruživanja kao i samo pohranjivanje realnih brojeva.

Drugim riječima, ako je \(\circ\) neka od operacija \(+, -, *, /\), onda za prikazive brojeve \(x\) i \(y\) vrijedi

\[ \fl(x \circ y) = (1 + \varepsilon) (x \circ y), \quad \text{ za neki } |\varepsilon| \leq u. \]

Relativna greška \(\varepsilon\) ovisi o \(x\), \(y\) te operaciji \(\circ\), no znamo da je po modulu manja od \(u\). To je zapravo jedino što znamo o izračunatom rezultatu, što ima vrlo zanimljive posljedice:

Zbrajanje i množenje u računalu nisu asocijativne operacije.
Ne vrijedi distributivnost množenja prema zbrajanju.

Jedino što i dalje vrijedi je komutativnost zbrajanja i množenja.

# Zbrajanje NIJE asocijativno.
# Objasnite zbog čega je došlo do razlike u sljedećem primjeru.
import math;

a = math.pow( 2.0, -53.0 ); # a = 2^(-53).

rez1 = (1.0 + a) + a;
rez2 = 1.0 + (a + a);

print( f'rez1 = {rez1:.16f}' );
print( f'rez2 = {rez2:.16f}' );

rez1 = 1.0000000000000000
rez2 = 1.0000000000000002

Širenje grešaka u egzaktnoj aritmetici#

Pretpostavimo sada da imamo egzaktne vrijednosti \(x \in \R\) i \(y \in \R\) i neke njihove aproksimacije \(\tilde{x}\) i \(\tilde{y}\) koje imaju malu relativnu grešku:

\[ \tilde{x} = (1+\varepsilon_x)x, \; \tilde{y} = (1+\varepsilon_y)y, \]

za malene \(\varepsilon_x\), \(\varepsilon_y\). Te greške su mogle nastati pohranjivanjem \(x\) i \(y\) u računalu, ali i na drugi način, na primjer, mjerenjem. Sada imamo sljedeće vrlo važno pitanje.

Egzaktni račun s operandima koji imaju grešku

Želimo provesti neki komplicirani izračun u kojem umjesto \(x\) i \(y\) koristimo \(\tilde{x}=(1+\varepsilon_x)x\) i \(\tilde{y}=(1+\varepsilon_y)y\). Kako će to utjecati na konačni rezultat? Hoće li se i on malo promijeniti?

Pojednostavljeno, zamislimo da je „komplicirani izračun” samo jedna od četiri osnovne operacije: neka je \(\circ\) jedna od operacija \(+\), \(-\), \(*\), \(/\). Neka je \(\varepsilon_\circ\) takav da vrijedi

\[ \tilde{x} \circ \tilde{y} = (x \circ y) (1 + \varepsilon_\circ). \]

Dakle, egzaktni rezultat bi bio \(x \circ y\), a mi smo dobili aproksimaciju \(\tilde{x} \circ \tilde{y}\) s relativnom greškom \(|\varepsilon_\circ|\). Ako su relativne greške \(|\varepsilon_x|\) i \(|\varepsilon_y|\) malene, da li je malena i relativna greška \(|\varepsilon_\circ|\)?

Analizirajmo jednu po jednu operaciju.

Množenje. Operacija množenja je bezopasna jer vrijedi

\[ \tilde{x} * \tilde{y} = x(1 + \varepsilon_x) * y(1 + \varepsilon_y) = xy (1 + \varepsilon_x + \varepsilon_y + \varepsilon_x \varepsilon_y) = (x*y) (1 + \varepsilon_*) \]

gdje je

\[ \varepsilon_* = \varepsilon_x + \varepsilon_y + \varepsilon_x \varepsilon_y \approx \varepsilon_x + \varepsilon_y, \]

Dijeljenje. Operacija dijeljenja je također bezopasna jer vrijedi

\[\begin{split} \begin{align*} \tilde{x} / \tilde{y} &= \frac{x(1 + \varepsilon_x)}{y(1 + \varepsilon_y)} \\ &= \frac{x}{y} (1 + \varepsilon_x) \left(1 - \varepsilon_y + \sum_{n=2}^{\infty} (-1)^n \varepsilon_y^n \right) \\ &\approx \frac{x}{y} (1 + \varepsilon_x)(1 - \varepsilon_y) \\ &\approx \frac{x}{y} (1 + \varepsilon_x - \varepsilon_y) \\ &= (x/y) (1 + \varepsilon_/), \end{align*} \end{split}\]

gdje smo ponovno pretpostavili da su \(\varepsilon_x\) i \(\varepsilon_y\) dovoljno mali da možemo zanemariti njihov produkt kao i \(\varepsilon_y^n\) za \(n \geq 2\) (uvjerite se u to kada je npr. \(|\varepsilon_x|, |\varepsilon_y| \leq 1.1 \cdot 10^{-16}\)).

Ponovno slijedi ista ocjena relativne greške kao i kod množenja:

\[ |\varepsilon_/| \lessapprox |\varepsilon_x - \varepsilon_y| \leq |\varepsilon_x| + |\varepsilon_y|, \]

što je uvijek maleno.

Zbrajanje i oduzimanje. Da ove operacije mogu biti problematične, vidi se odmah iz slučaja u kojem je egzaktni rezultat \(x+y=0\), a aproksimativni \(\tilde{x} + \tilde{y} \neq 0\), što se može dogoditi. Tada bi relativna greška bila beskonačna. Napravimo analizu kao i prije; pretpostavimo \(x + y \neq 0\). Tada je:

\[\begin{split}\begin{align*} \tilde{x} + \tilde{y} &= x(1 + \varepsilon_x) + y(1 + \varepsilon_y) \\ &= (x+y) \left( 1 + \frac{x \varepsilon_x + y \varepsilon_y}{x+y} \right) \\ &= (x+y) (1 + \varepsilon_+), \end{align*} \end{split}\]

pa je

\[ \varepsilon_+ = \frac{x}{x+y} \varepsilon_x + \frac{y}{x+y} \varepsilon_y. \]

Relativna greška će ovisiti o tome koliko je \(x+y\) blizu \(0\). Uočimo prvo jednu situaciju kojoj je greška malena.

(a) Pretpostavimo da zbrajamo brojeve \(x\) i \(y\) istog predznaka. Tada je:

\[ \frac{|x|}{|x+y|} = \frac{|x|}{|x|+|y|}, \quad \frac{|y|}{|x+y|} = \frac{|y|}{|x|+|y|}, \]

pa je

\[ |\varepsilon_+| \leq \frac{|x|}{|x+y|} |\varepsilon_x| + \frac{|y|}{|x+y|} |\varepsilon_y| \leq \left( \frac{|x|}{|x|+|y|} + \frac{|y|}{|x|+|y|} \right) \max\{|\varepsilon_x|, |\varepsilon_y|\} = \max\{|\varepsilon_x|, |\varepsilon_y|\}. \]

(b) Pretpostavimo da zbrajamo brojeve \(x\) i \(y\) različitog predznaka. Ako vrijedi da je \(|x+y| \ll |x|, |y|\), onda može nastupiti problem jer u izrazu

\[ |\varepsilon_+| \leq \frac{|x|}{|x+y|} |\varepsilon_x| + \frac{|y|}{|x+y|} |\varepsilon_y| \]

koeficijenti koji množe \(|\varepsilon_x|\) i \(|\varepsilon_y|\) mogu biti vrlo veliki! Umjesto zbrajanja brojeva različitog predznaka, obično ekvivalentno promatramo oduzimanje brojeva istog predznaka.

Katastrofalno kraćenje

Opasna situacija u kojoj rezultat može imati veliku relativnu grešku iako operandi imaju malu relativnu grešku može nastupiti kada:

Oduzimamo brojeve \(x\) i \(y\) istog predznaka.
Očekivani rezultat \(x-y\) je po modulu puno manji od \(|x|\) i \(|y|\).

Dakle, brojevi \(x\) i \(y\) su bliski i može doći do tzv. katastrofalnog kraćenja.

Primjer 1.9

Ovaj efekt ćemo ilustrirati na jednom primjeru. Radi jednostavnosti, pretpostavimo da koristimo računalo s aritmetikom u bazi 10 koje koristi 3 dekadske znamenke za zapis mantise. Dani su brojevi

\[\begin{split} \begin{align*} x &= 8.8866 = 8.8866 \cdot 10^0, \\ y &= 8.8844 = 8.8844 \cdot 10^0. \end{align*} \end{split}\]

i želimo na računalu izračunati \(z := x-y\). Egzaktni rezultat je

\[\begin{split} \begin{align*} z = x-y &= 8.8866 \cdot 10^0 - 8.8844 \cdot 10^0 \\ &= 0.0022 \cdot 10^0 \\ &= 2.2 \cdot 10^{-3}. \end{align*} \end{split}\]

Spremanjem brojeva \(x\) i \(y\) u naše računalo, oni se moraju zakružiti na 3 dekadske znamenke iza decimalne točke:

\[\begin{split} \begin{align*} \tilde{x} &= \fl(x) = 8.887 \cdot 10^0, \\ \tilde{y} &= \fl(y) = 8.884 \cdot 10^0. \end{align*} \end{split}\]

Relativna greška nastala zaokruživanjem je malena: \(|\varepsilon_x| = \frac{|x - \fl(x)|}{|x|} \leq 5 \cdot 10^{-5}\), \(|\varepsilon_y| = \frac{|y - \fl(y)|}{|y|} \leq 5 \cdot 10^{-5}\).

Sada računamo razliku u računalu:

\[\begin{split} \begin{align*} \tilde{z} := \fl(x) - \fl(y) &= 8.887 \cdot 10^0 - 8.884 \cdot 10^0 \\ &= 0.003 \cdot 10^0 \\ &= 3.000 \cdot 10^{-3}. \end{align*} \end{split}\]

U zadnjem koraku smo napravili normalizaciju kako bi se rezultat spremio u varijablu u računalu. Kolika je relativna greška izračunatog rezultata u odnosu na egzaktni?

\[ \frac{|\tilde{z} - z|}{|z|} = \frac{ 3.000 \cdot 10^{-3} - 2.2 \cdot 10^{-3}}{2.2 \cdot 10^{-3}} \approx 0.36. \]

Iako je relativna greška u ulaznim podacima \(\tilde{x}\) i \(\tilde{y}\) bila manja od \(5 \cdot 10^{-5}\), relativna greška nakon samo jednog oduzimanja je puno veća (\(\approx 0.36\))! Vidimo da izračunata vrijednost \(\tilde{z}=3 \cdot 10^{-3}\) i egzaktna \(z=2.2\cdot 10^{-3}\) nemaju čak niti prvu znamenku jednaku!

Uočimo da ovdje nije krivac sama operacija oduzimanja! Razlika \(\tilde{x} - \tilde{y}\) je bila izračunata egzaktno na računalu! Uzrok krivog rezultata je činjenica da ne oduzimamo egzaktne vrijednosti \(x\) i \(y\) nego njihove aproksimacije \(\tilde{x}\) i \(\tilde{y}\).

Za one koje žele znati više. Gornji primjer možemo simulirati i u Pythonu. Biblioteka mpmath omogućava računanje s brojevima čiji binarni zapis ima proizvoljnu duljinu mantise, pa sličan efekt postižemo ograničavanjem mantise na 12 binarnih znamenki.

import mpmath;

x = 8.8866;
y = 8.8844;

# "Egzaktna" razlika izračunata u standardnoj aritmetici sa 52 binarne znamenke u mantisi.
z = x - y;
print( f'"Egzaktna" razlika z = x-y = {z}\n' );

# Aritmetika koja koristi samo 12 binarnih znamenki u mantisi.
mpmath.mp.prec = 12;
x_tilde = mpmath.mpf(x);     # Spremimo broj x u "računalo". 
y_tilde = mpmath.mpf(y);     # Spremimo broj y u "računalo".
z_tilde = x_tilde - y_tilde; # Izračunamo razliku na "računalu".

print( 'Rezultati u aritmetici sa 12 binarnih znamenki u mantisi: ' );
print( 'x_tilde =', repr(x_tilde) );
print( 'y_tilde =', repr(y_tilde) );
print( 'z_tilde = x_tilde - y_tilde =', repr(z_tilde) );

# float(z_tilde) služi za konverziju z_tilde natrag u standarnu aritmetiku.
relativna_greska = abs( z - float(z_tilde) ) / abs(z);
print( '\nRelativna greška z_tilde u odnosu na z =', relativna_greska );

"Egzaktna" razlika z = x-y = 0.002200000000000202

Rezultati u aritmetici sa 12 binarnih znamenki u mantisi: 
x_tilde = mpf('8.88672')
y_tilde = mpf('8.88281')
z_tilde = x_tilde - y_tilde = mpf('0.00390625')

Relativna greška z_tilde u odnosu na z = 0.775568181818019

Primjeri izbjegavanja katastrofalnog kraćenja#

U nekim situacijama je moguće malo preurediti formulu za računanje tako da izbjegnemo opasnost potencijalno katastrofalnog kraćenja. U ovoj cjelini ćemo vidjeti par jednostavnih primjera.

Primjer 1.10

Rješavamo kvadratnu jednadžbu \(ax^2 + bx + c = 0\) standardnom formulom

\[ x_{1, 2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}. \]

Prvo, broj potrebnih operacija možemo malo smanjiti tako da prvo podijelimo jednadžbu sa \(a\) i svedemo na oblik \(x^2 + px + q = 0\) za \(p = b/a\), \(q = c/a\), pa rješenje glasi

\[ x_{1, 2} = \frac{-p \pm \sqrt{p^2 - 4q}}{2} = \frac{-p}{2} \pm \sqrt{\left( \frac{p}{2} \right)^2 - q}. \]

Kad bismo ovom formulom rješavali jednadžbu \(x^2 - 56 x + 1 = 0\), u aritmetici s točnosti od \(5\) dekadskih znamenki, dobili bismo

\[\begin{split} \begin{align*} x_1 &= 28 - \sqrt{783} = 28 - 27.982 = 0.018 = 1.8000 \cdot 10^{-2}, \\ x_2 &= 28 + \sqrt{783} = 28 + 27.982 = 55.982 = 5.5982 \cdot 10^1, \\ \end{align*} \end{split}\]

dok su egazktna rješenja

\[\begin{split} \begin{align*} x_1 &= 0.0178628 = 1.7863 \cdot 10^{-2}, \\ x_2 &= 55.982137 = 5.5982 \cdot 10^1. \end{align*} \end{split}\]

Rješenje \(x_1\) ima samo dvije znamenke točne i relativna greška je velika (\(7.7 \cdot 10^{-3}\)), dok je \(x_2\) posve točan. U izrazu za \(x_1\) imamo oduzimanje dva bliska broja i došlo je do katastrofalnog kraćenja.

Formulu možemo popraviti tako da prvo izračunamo nultočku koja je veća po modulu (predznak ispred korijena je suprotni od predznaka od b):

\[ x_2 = \frac{-(b + \text{sign}(b) \sqrt{b^2 - 4ac})}{2a} = \frac{-p}{2} - \text{sign}(p) \sqrt{\left( \frac{p}{2} \right)^2 - q}, \]

a zatim manji korijen izračunamo preko Vietove formule:

\[ x_1 = \frac{c}{ax_2} = \frac{q}{x_2}. \]

Sada u formulama imamo samo zbrajanje brojeve istog predznaka i nema više kraćenja za \(x_1\). Kada na ovaj način izračunamo \(x_1\) dobivamo

\[ x_1 = \frac{1}{x_2} = 0.0178628 \approx 1.7863 \cdot 10^{-2}, \]

što se podudara s egzaktnim rješenjem spremljenim u varijablu.

Uočite da potencijalno katastrofalno kraćenje u pod korijenom ne možemo izbjeći. No kada pod korijenom treba ispasti jako maleni broj, to znači da su rješenja kvadratne jednadžbe jako bliska. To je odraz nestabilnosti rješenja: nultočke takvih polinoma su jako osjetljive na male promjene koeficijenata (vidi cjelinu Uvjetovanost računanja nultočki polinoma).

Primjer 1.11

Ako treba izračunati vrijednost izraza

\[ y = \sqrt{x+\delta} - \sqrt{x}, \]

gdje je \(|\delta|\) vrlo malen broj, onda imamo potencijalno katastrofalno kraćenje. Njega možemo izbjeći „deracionalizacijom”:

\[ y = (\sqrt{x+\delta} - \sqrt{x}) \cdot \frac{\sqrt{x+\delta} + \sqrt{x}}{\sqrt{x+\delta} + \sqrt{x}} = \frac{\delta}{\sqrt{x+\delta} + \sqrt{x}}. \]

Sada više nema potencijalnog oduzimanja bliskih brojeva.

Slično, ako treba izračunati vrijednost izraza

\[ y = \cos(x+\delta) - \cos x, \]

potencijalno katastrofalno kraćenje izbjegavamo konverzijom sume trigonometrijskih funkcija u produkt:

\[ y = -2 \sin \frac{\delta}{2} \sin \left( x + \frac{\delta}{2} \right). \]

Širenje grešaka u aritmetici računala#

Kada provodimo računanje u aritmetici računala, dolazi do grešaka zaokruživanja:

Ulazni podaci u algoritam se zaokružuju čim ih spremimo u varijable.
Rezultat svake aritmetičke operacije se ponovno zaokružuje da bi se spremio u varijablu.

Kako raditi analizu svih nastalih grešaka?

Egzaktni račun s pertubiranim podacima

Ključna ideja je prikazati konačni rezultat nastao u aritmetici računala kao egzaktni račun koji je proveden s perturbiranim podacima.

Preciznije:

Želimo izračunati \(y = f(x)\).
Na računalu smo umjesto \(y\) zbog zaokruživanja dobili neku vrijednost \(\tilde{y}\).
Sada želimo pokazati da postoji \(\tilde{x}\) takav da je \(\tilde{y} = f(\tilde{x})\).

Dakle, ono što smo dobili na računalu nije \(f(x)\) nego \(f(\tilde{x})\).

Ako pokažemo da je \(\tilde{x}\) „blizu” x, onda očekujemo da je i \(\tilde{y} = f(\tilde{x})\) „blizu” \(f(x)\). To naravno ovisi o funkciji \(f\) za koju treba napraviti teoriju perturbacija, tj. odrediti njezinu uvjetovanost.

Osnovne aritmetičke operacije na računalu jako dobro podržavaju ovu ideju. Podsjetimo se, te operacije zadovoljavaju

\[ \fl(x \circ y) = (1 + \varepsilon) (x \circ y), \quad \circ \in \{+, -, *, / \}. \]

Sa \(\fl(\text{izraz})\) ćemo označavati rezultat računanja izraza \(\text{izraz}\) na računalu. Rezultat svake od operacija provedene na računalu možemo zapisati kao rezultat egzaktne operacije ali sa podacima koji su perturbirani:

Zbrajanje i oduzimanje: \(\fl(x \pm y) = (1+\varepsilon) (x \pm y) = \underbrace{(1+\varepsilon) x}_{\tilde{x}} \pm \underbrace{(1+\varepsilon) y}_{\tilde{y}} = \tilde{x} \pm \tilde{y}\).
Množenje: \(\fl(x * y) = (1+\varepsilon) (x * y) = \underbrace{(1+\varepsilon) x}_{\tilde{x}} \; * \underbrace{y}_{\tilde{y}} = \tilde{x} * \tilde{y}\).
Dijeljenje: \(\fl(x / y) = (1+\varepsilon) (x / y) = \underbrace{(1+\varepsilon) x}_{\tilde{x}} \; / \underbrace{y}_{\tilde{y}} = \tilde{x} / \tilde{y}\).

Ovakav pristup koristimo i kada imamo više operacija.

Primjer 1.12

Pretpostavimo da u računalu želimo izračunati izraz \(a*b+c+d\), pri čemu su \(a, b, c, d\) već spremljeni u računalo. Sada ćemo primijeniti pravila aritmetike u računalu; u svakom koraku je označena crvenim operacija koju raspisujemo. Slijedi da postoje \(|\varepsilon_1|, |\varepsilon_2|, |\varepsilon_3| \leq u\) takvi da:

\[\begin{split} \begin{align*} \fl(a \red{*} b) &= ab(1 + \eps_1) \\ \fl(a * b \red{+} c) &= (\fl(a*b) + c) (1 + \eps_2) = (ab(1 + \eps_1) + c) (1 + \eps_2) \\ \fl(a*b+c\red{+}d) &= (\fl(a*b+c) + d) (1 + \eps_3) \\ &= ( (ab(1 + \eps_1) + c) (1 + \eps_2) + d ) (1 + \eps_3) \\ &= \tilde{a} \tilde{b} + \tilde{c} + \tilde{d}, \end{align*} \end{split}\]

gdje je (na primjer)

\[\begin{split} \begin{align*} \tilde{a} &= a(1 + \varepsilon_1)(1 + \varepsilon_3) \approx a(1 + \varepsilon_1 + \varepsilon_3) = a(1 + \varepsilon_a), \quad |\varepsilon_a| \leq |\varepsilon_1| + |\varepsilon_3| \leq 2u, \\ \tilde{b} &= b(1 + \varepsilon_2) = b(1 + \varepsilon_b), \quad |\varepsilon_b| = |\varepsilon_2| \leq u, \\ \tilde{c} &= c(1 + \varepsilon_2)(1 + \varepsilon_3) \approx c(1 + \varepsilon_2 + \varepsilon_3) = c(1 + \varepsilon_c), \quad |\varepsilon_c| \leq |\varepsilon_2| + |\varepsilon_3| \leq 2u, \\ \tilde{d} &= d(1 + \varepsilon_3) = d(1 + \varepsilon_d), \quad |\varepsilon_d| = |\varepsilon_3| \leq u. \end{align*} \end{split}\]

Vrijednost \(\fl(ab+c+d)\) koju smo dobili na računalu je jednaka egzaktnoj vrijednosti \(\tilde{a}\tilde{b} + \tilde{c} + \tilde{d}\) gdje su \(\tilde{a}\), \(\tilde{b}\), \(\tilde{c}\), \(\tilde{d}\) brojevi dobiveni malim relativnim perturbacijama originalnih \(a\), \(b\), \(c\), \(d\).

Što ako brojevi \(a, b, c, d\) na početku nisu bili spremljeni u računalo? Opet slično, prilikom spremanja tih brojeva u računalo dobivamo redom brojeve \(\fl(a)\), \(\fl(b)\), \(\fl(c)\), \(\fl(d)\) takve da je

\[\begin{split} \begin{align*} \fl(a) &= a(1 + \varepsilon_A), \quad |\varepsilon_A| \leq u, \\ \fl(b) &= b(1 + \varepsilon_B), \quad |\varepsilon_B| \leq u, \\ \fl(c) &= c(1 + \varepsilon_C), \quad |\varepsilon_C| \leq u, \\ \fl(d) &= d(1 + \varepsilon_D), \quad |\varepsilon_D| \leq u \end{align*} \end{split}\]

pa zapravo računamo \(\fl(ab+c+d) = \fl\left( \fl(a) * \fl(b) + \fl(c) + \fl(d) \right)\). Svaka od perturbacija koje smo gore izračunali samo dobije još jedan faktor oblika \((1+\varepsilon)\).

Vidimo da svaka pojedina aritmetička operacija u kojoj sudjeluje neki ulazni podatak množi njegovu perturbaciju jednim dodatnim faktorom oblika \((1+\varepsilon)\) za neki \(|\varepsilon| \leq u\). Nakon \(n\) operacija stoga imamo

\[ \tilde{a} = a(1 + \eps_1)(1 + \eps_2)\ldots (1 + \eps_n) \approx a(1 + \underbrace{\eps_1 + \eps_2 \ldots + \eps_n}_{\eps_a}) , \quad |\eps_a|\leq nu. \]

Kada je \(u \approx 10^{-16}\), broj operacija \(n\) u kojima sudjeluje \(a\) može biti zaista jako velik (na primjer, milijardu), a da relativna perturbacija \(\eps_a\) i dalje bude vrlo malena.

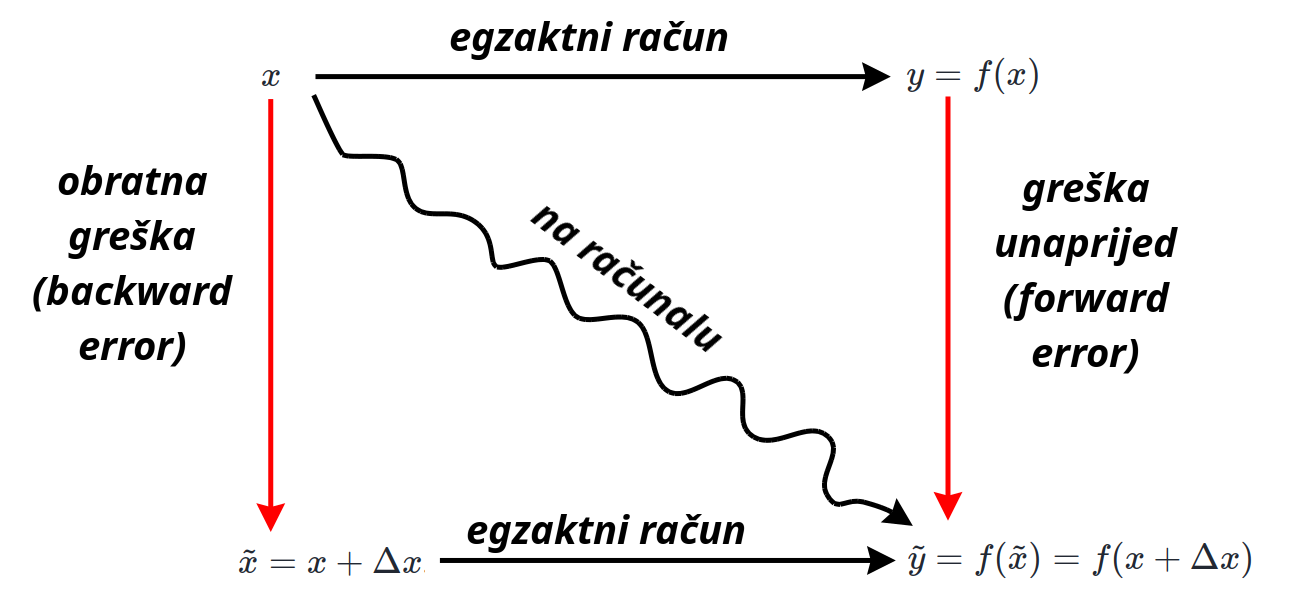
Greške unaprijed i greške unatrag#

Kako smo i najavili, u gornjem primjeru smo prikazali rezultat računanja izraza \(y=ab+c+d\) u aritmetici računala kao \(\tilde{y} = \tilde{a}\tilde{b}+\tilde{c}+\tilde{d}\), gdje su \(\tilde{a}\), \(\tilde{b}\), \(\tilde{c}\), \(\tilde{d}\) nastale malenim perturbacijama od \(a\), \(b\), \(c\), \(d\) te smo znali odrediti točno koliko su malene te perturbacije. Međutim, nas zapravo zanima koliko je daleko \(\tilde{y}\) od \(y\). Vrlo je bitno razlikovati ta dva pojma.

Definicija 1.13 (Greške unaprijed i unatrag)

Pretpostavimo da neki algoritam na ulazu prima vrijednost \(x\) i njegov cilj je izračunati \(y = f(x)\). Implementacijom algoritma na računalu smo umjesto \(y\) dobili vrijednost \(\tilde{y}\).

Neka je \(\tilde{y} = y + \Delta y\). Kažemo da je \(\Delta y\) greška unaprijed algoritma. Engleski: forward error.

Pretpostavimo da smo dokazali da vrijedi \(\tilde{y} = f(\tilde{x}) = f(x + \Delta x)\) za neki \(\tilde{x} = x + \Delta x\). Kažemo da je \(\Delta x\) greška unatrag ili povratna greška ili obratna greška algoritma. Engleski: backward error.