Ctrl+K

Interpolacija polinomima

Hide code cell source 
import numpy as np;
import scipy as sc;
import matplotlib.pyplot as plt;

%matplotlib inline

3.1. Interpolacija polinomima#

Opis problema. Zadana je funkcija \(f : [a, b] \to \R\). Želimo odrediti polinom \(p\) takav da vrijedi \(p(x_0) = f(x_0)\), …, \(p(x_n) = f(x_n)\), gdje su \(x_0, \dots, x_n \in [a, b]\) odabrane međusobno različite točke. Kažemo da takav polinom interpolira funkciju \(f\) u čvorovima interpolacije \(x_0, \ldots, x_n\). Uočimo da nam u cijelom ovom poglavlju nije potrebna pretpostavka da su točke \(x_k\) uzlazno sortirane; to će biti vrlo bitno za neke od dokaza koji slijede.

Odgovor na pitanje postoji li takav polinom \(p\), te je li jedinstven daje sljedeći teorem.

Teorem 3.4 (Egzistencija interpolacijskog polinoma)

Neka je \(n \in \N \cup \{0\}\). Za zadane parove \((x_k, f_k)\), \(k=0, \ldots, n\), gdje su svi \(x_0, \dots, x_n\) međusobno različiti, postoji jedinstveni interpolacijski polinom \(\varphi \in \mathcal{P}_n\),

(3.1)#\[ \varphi(x) := p_n(x) = a_0 + a_1 x + \ldots + a_n x^n\]

takav da za svaki \(k=0, \ldots, n\) vrijedi \(p_n(x_k) = f_k\).

Ovdje smo sa \(\mathcal{P}_n\) označili skup svih polinoma stupnja manjeg ili jednakog \(n\).

Dokaz.

Neka je \(p_n \in \mathcal{P}_n\) polinom stupnja \(\leq n\) čiji koeficijenti su \(a_0, \ldots, a_n\) kao u (3.1). Uvjete interpolacije napišemo u obliku sustava linearnih jednadžbi s nepoznanicama \(a_0, \ldots, a_n\):

\[\begin{split}\begin{align*} p_n(x_0) &= a_0 + a_1 x_0 + \ldots + a_n x_0^n = f_0 \\ p_n(x_1) &= a_0 + a_1 x_1 + \ldots + a_n x_1^n = f_1 \\ & \vdots \\ p_n(x_n) &= a_0 + a_1 x_n + \ldots + a_n x_n^n = f_n. \end{align*}\end{split}\]

Pokažimo da je matrica ovog sustava regularna ako i samo ako su čvorovi \(x_0, \ldots, x_n\) različiti. Tada sustav ima jedistveno rješenje, tj. postoji polinom \(p_n\) i jedinstven je.

Determinanta sustava je tzv. Vandermondeova determinanta

\[\begin{split}D_n = \left| \begin{array}{ccccc} 1 & x_0 & x_0^2 & \ldots & x_0^n \\ 1 & x_1 & x_1^2 & \ldots & x_1^n \\ & & \vdots & & \\ 1 & x_n & x_n^2 & \ldots & x_n^n \end{array} \right|.\end{split}\]

Definirajmo još sličnu determinantu koja u zadnjem retku umjesto fiksne vrijednosti \(x_n\) ima varijablu \(x\):

\[\begin{split}V_n(x) = \left| \begin{array}{ccccc} 1 & x_0 & x_0^2 & \ldots & x_0^n \\ 1 & x_1 & x_1^2 & \ldots & x_1^n \\ & & \vdots & & \\ 1 & x & x^2 & \ldots & x^n \end{array} \right|.\end{split}\]

Vrijedi \(D_n = V_n(x_n)\).

Razvijmo \(V_n(x)\) po zadnjem retku i uočimo:

  • \(V_n(x)\) je polinom stupnja najviše \(n\) u varijabli \(x\);

  • koeficijent tog polinoma uz \(x^n\) je upravo \(D_{n-1}\) jer ga dobijemo kada prekrižimo zadnji redak i stupac od \(V_n(x)\).

Uočimo još sljedeće:

\[ V_n(x_0) = V_n(x_1) = \ldots = V_n(x_{n-1}) = 0\]

jer svaka od ovih determinanti ima dva jednaka retka, pa je njezina vrijednost \(0\). Stoga su \(x_0, \ldots, x_{n-1}\) nultočke polinoma \(V_n(x)\). Taj polinom je stupnja \(n\) i ima vodeći koeficijent \(D_{n-1}\), pa stoga mora biti jednak

\[ V_n(x) = D_{n-1}(x-x_0)(x-x_1)\cdots (x-x_{n-1}).\]

Uvrstimo \(x=x_n\) i dobivamo

\[ D_n = V_n(x_n) = D_{n-1}(x_n-x_0)(x_n-x_1)\cdots (x_n-x_{n-1}).\]

Sada isti postupak primijenimo na \(D_{n-1}\), pa na \(D_{n-2}\), sve do \(D_0 = 1\), te dobivamo:

\[\begin{split}\begin{align*} D_n &= D_{n-1} (x_n-x_0)(x_n-x_1)\cdots (x_n-x_{n-1}) \\ &= D_{n-2} (x_{n-1}-x_0)(x_{n-1}-x_1)\cdots (x_{n-1}-x_{n-2}) (x_n-x_0)(x_n-x_1)\cdots (x_n-x_{n-1}) \\ &= \ldots = \prod_{0 \leq j < i \leq n} (x_i - x_j). \end{align*}\end{split}\]

Dakle, \(D_n \neq 0\) ako i samo ako su svi čvorovi \(x_k\) različiti, i tada postoji interpolacijski polinom stupnja najviše \(n\) i on je jedinstven.

Upozorenje

U nastavku ćemo se baviti raznim oblicima interpolacijskog polinoma. No to će uvijek biti jedan te isti polinom, čiju smo jedinstvenost pokazali u gornjem teoremu. Jedino što će se mijenjati je izbor baze u kojoj prikazujemo taj uvijek isti polinom.

Sljedeći primjer pokazuje kako izbor kanonske baze za prikaz interpolacijskog polinoma može biti problematičan.

Primjer. Pronađimo interpolacijski polinom \(p_{40}\) stupnja \(40\) zapisan u standardnoj bazi potencija koji interpolira funkciju

\[ f(x) = \sin{x}\]

na ekvidistantnoj mreži čvorova \(x_k = k \frac{\pi}{2}\) na intervalu \([0, 20\pi]\).

Matrica sustava koji trebamo riješiti da bismo odredili nepoznate koeficijente je Vandermondeova, kao u dokazu Teorema 3.4. Odredimo njezinu uvjetovanost.

Hide code cell content 
# Čvorovi interpolacije: 41 ekvidistantna točka između 0 i 20pi, uključujući rubove.
x = np.linspace(0.0, 20.0*np.pi, num=41);

# Vandermondeova matrica za čvorove interpolacije.
A = np.vander(x, increasing=True);

# Uvjetovanost od A.
print(np.linalg.cond(A));

3.2572831130142366e+72

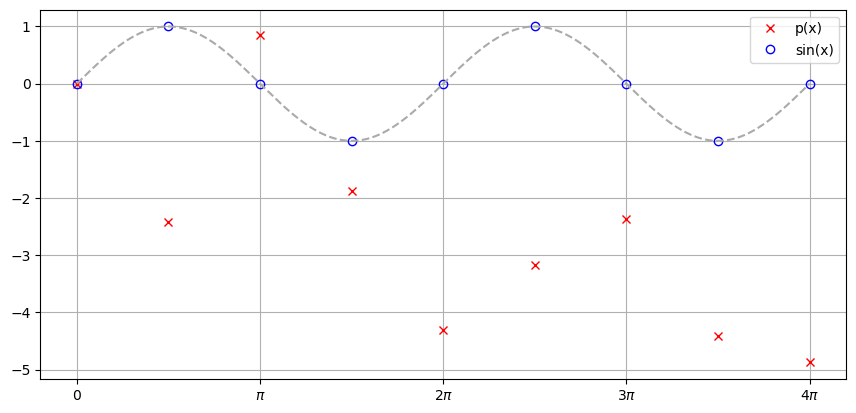
Uvjetovanost matrice sustava je jednaka \(\approx 3.26 \cdot 10^{72}\), što je iznimno veliko i stoga očekujemo velike greške prilikom rješavanja sustava. Zaista, ako odredimo koeficijente interpolacijskog polinoma \(p_{40}\) kao rješenja linearnog sustava, vrijednosti \(p_{40}(x_k)\) bi se morale podudarati sa \(f(x_k)=\sin(x_k)\) u čvorovima interpolacije \(x_k\). No zbog velikih grešaka u rješavanju sustava vidimo da to nije slučaj, te se na donjoj slici crvene oznake – vrijednosti \(p(x_k)\) – ni približno ne podudaraju s plavim oznakama – vrijednostima \(f(x_k) = \sin(x_k)\).

Hide code cell source 
# Vrijednosti funkcije f u čvorovima interpolacije.
f = np.sin(x);

# Rješenje sustava A*koef = f daje koeficijente interpolacijskog polinoma.
koef = np.linalg.solve(A, f);

# Napravimo polinom s koeficijentima koef[0], koef[1], ...
p = np.polynomial.polynomial.Polynomial(koef);

# Nacrtamo vrijednosti od p(x) u čvorovima interpolacije, te sin(x) u čvorovima interpolacije.
# Uzmimo samo prvih 10 čvorova.
x_first = x[0:9];
plt.figure(figsize=[10.4, 4.8]);
plt.plot(x_first, p(x_first), 'rx', label='p(x)');
plt.plot(x_first, np.sin(x_first), 'bo', label='sin(x)', fillstyle='none');

# Nacrtamo još i graf funkcije sin(x).
x_all = np.linspace(0, 4*np.pi, 1000);
plt.plot(x_all, np.sin(x_all), '--', color='#aaaaaa');

plt.legend();
plt.grid();
plt.xticks(ticks=[0, np.pi, 2*np.pi, 3*np.pi, 4*np.pi], labels=['0', '$\pi$', '2$\pi$', '3$\pi$', '4$\pi$']);
plt.show();
_images/b14e6a7d9c6d8e8463b44416959e8e2f1f7e888bc4dfae8ef0c7e0948efe7e6b.png

Stoga je problematično računati interpolacijske polinome zapisane u kanonskoj bazi, pogotovo one imalo većeg stupnja.

Tipično, Vandermondeove matrice imaju veliku uvjetovanost za većinu izbora čvorova interpolacije. Pokušajte sami modificirati gornje programe u Pythonu i odrediti uvjetovanosti za razne druge mreže čvorova interpolacije na intervalu \([0, 20\pi]\): na primjer, za mrežu \(x_k = \frac{20 \pi}{k}\), \(k=1, \ldots, 41\).

S druge strane, postoje i dobre mreže čvorova za interpolaciju, ali takvi čvorovi su u \(\C\), a ne u \(\R\)! Najvažniji takav primjer su kompleksni korijeni iz jedinice:

\[ x_k = e^{2\pi \ii k /(n+1)} = \cos \frac{2 k \pi}{n+1} + \ii \sin \frac{2k \pi}{n+1}, \quad k=0, \ldots, n. \]

Tada je Vandermondova matrica jednaka \(V_n = \sqrt{n+1} \cdot U\), gdje je \(U\) unitarna matrica, pa je uvjetovanost od \(V_n\) jednaka \(1\), što je idealna uvjetovanost! Ovo je podloga za tzv. brzu Fourierovu transformaciju (FFT), proglašenu najvažnijim algoritmom u povijesti!

Napomena

Zaključimo: ako je zadano \(n\) čvorova interpolacije, da bismo prikazali polinom u kanonskoj bazi, potrebno je riješiti sustav linearnih jednadžbi s potencijalno vrlo visokom uvjetovanosti. Osim toga, rješavanje tog sustava kojim određujemo koeficijente polinoma ima veliku vremensku složenost \(\bigO(n^3)\).

Lagrangeov oblik interpolacijskog polinoma#

Ako u prostoru polinoma \(\mathcal{P}_n\) odaberemo neku bazu \(\{ \varphi_0, \ldots, \varphi_n \}\), onda interpolacijski polinom možemo prikazati u obliku

\[ p_n(x) = a_0 \varphi_0(x) + a_1 \varphi_1(x) + \ldots + a_n \varphi_n(x).\]

Linearni sustav za nepoznate koeficijente \(a_0, \ldots, a_n\) ima oblik

\[\begin{split}\begin{align*} p_n(x_0) &= a_0 \varphi_0(x_0) + a_1 \varphi_1(x_0) + \ldots + a_n \varphi_n(x_0) = f_0 \\ p_n(x_1) &= a_0 \varphi_0(x_1) + a_1 \varphi_1(x_1) + \ldots + a_n \varphi_n(x_1) = f_1 \\ & \vdots \\ p_n(x_n) &= a_0 \varphi_0(x_n) + a_1 \varphi_1(x_n + \ldots + a_n \varphi_n(x_n) = f_n, \end{align*}\end{split}\]

pa je njegova matrica sustava

\[\begin{split}\mb{cccc} \varphi_0(x_0) & \varphi_1(x_0) & \ldots & \varphi_n(x_0) \\ \varphi_0(x_1) & \varphi_1(x_1) & \ldots & \varphi_n(x_1) \\ & & \vdots & \\ \varphi_0(x_n) & \varphi_1(x_n) & \ldots & \varphi_n(x_n) \me.\end{split}\]

Možemo li pronaći bazu u kojoj je matrica ovog sustava jedinična?

Definicija 3.5 (Lagrangeova baza za interpolaciju)

Lagrangeova baza \(\{\ell_0, \ell_1, \ldots, \ell_n\}\) u prostoru polinoma \(\mathcal{P}_n\) je ona baza za koju je matrica sustava za interpolaciju upravo jedinična matrica.

(U gornji sustav, tj. matricu, uvrstimo \(\varphi_k = \ell_k\).)

Tada uopće neće biti potrebno rješavati sustav, nego ćemo moći odmah očitati rješenje: \(k\)-ta jednadžba prelazi jednostavno u \(a_k = f_k\), pa polinom glasi

(3.2)#\[ p_n(x) = f_0 \ell_0(x) + f_1 \ell_1(x) + \ldots + f_n \ell_n(x).\]

Jednadžba (3.2) daje Lagrangeov oblik interpolacijskog polinoma. Kako bi matrica sustava za koeficijente bila jedinična, za svaki \(k=0, \ldots, n\) mora vrijediti

\[\begin{split} \ell_k(x_i) = \delta_{ki} = \left\{\begin{array}{ll} 0, & i \neq k, \\ 1, & i = k. \end{array}\right.\end{split}\]

Uočimo da je polinom \(\ell_k\) zapravo interpolacijski polinom koji u čvoru \(x_k\) poprima vrijednost \(1\), a u svim ostalim čvorovima vrijednost \(0\). Stoga taj polinom postoji po Teoremu 3.4.

S druge strane, možemo lako pronaći i eksplicitnu formulu za taj polinom:

(3.3)#\[ \ell_k(x) = \frac{(x-x_1)(x-x_2)\cdots (x-x_{k-1})(x-x_{k+1}) \cdots (x-x_n)}{(x_k-x_1)(x_k-x_2)\cdots (x_k-x_{k-1})(x_k-x_{k+1}) \cdots (x_k-x_n)} =: \frac{\omega_k(x)}{\omega_k(x_k)}.\]
Definicija 3.6

Neka su \(x_0, x_1, \ldots, x_n\) čvorovi interpolacije. Polinom

\[ \omega(x) := (x-x_0)(x-x_1) \cdots (x-x_n) = \prod_{i=0}^n (x-x_i)\]

zovemo polinom čvorova.

Koristeći polinom čvorova, elemente Lagrangeove baze možemo zapisati i ovako:

\[ \ell_k(x) = \frac{\omega(x)}{(x-x_k)\omega_k(x_k)},\]

a lako se, derivacijom produkta, vidi da je \(\omega_k(x_k) = \omega'(x_k)\), pa stoga

(3.4)#\[ p_n(x) = \omega(x) \sum_{k=0}^n \frac{f_k}{(x-x_k)\omega'(x_k)}.\]

Napomena

Koristeći formulu (3.4), vrijednost \(p_n(x)\) za zadanu točku \(x\) možemo izračunati u \(\bigO(n)\): toliko operacija nam treba za računanje produkta \(\omega(x)\) i za računanje sume u (3.4).

To vrijedi u slučaju da unaprijed izračunamo i u nekom polju zapamtimo sve vrijednosti \(\omega'(x_k) = \omega_k(x_k)\). Za tu pripremnu fazu nam treba ukupno \(\bigO(n^2)\) operacija, a nakon toga, izračun svakog novog \(p_n(x)\) zahtijeva samo \(\bigO(n)\) operacija. To je bitno efikasnije od zapisa u kanonskoj bazi, koja je trebala \(\bigO(n^3)\) operacija u pripremnoj fazi za rješavanje sustava.

Iako gornja napomena sugerira da je Lagrangeova baza pogodna za računanje interpolacijskog polinoma, ona se ipak uglavnom koristi za teoretske svrhe, kao što ćemo vidjeti u narednim cjelinama. Iznimno, varijanta koja koristi baricentričku formu Lagrangeovog interpolacijskog polinoma je pogodna i za implementaciju na računalu.

Newtonov oblik interpolacijskog polinoma#

Primijetimo da Lagrangeov oblik nije pogodan za naknadno dodavanje čvorova, tj. postupno povećanje stupnja interpolacije. Naime, ako dodamo novi čvor \(x_{n+1}\), promijenit će se svi elementi baze \(\ell_0, \ldots, \ell_n\) i morat ćemo ih ponovno izračunati.

Za tu svrhu puno je pogodniji tzv. Newtonov oblik interpolacijskog polinoma. Njega ćemo izvesti upravo tako da, počevši od trivijalnog interpolacijskog polinoma stupnja \(0\), u svakom koraku dodajemo po jedan novi čvor.

Polinom \(p_0\) koji interpolira funkciju \(f\) u čvoru \(x_0\) glasi

\[ p_0(x) = f_0.\]

Dodajmo još jedan čvor \(x_1\). Polinom \(p_1\) dobijemo iz \(p_0\) dodavanjem korekcije \(r_1\):

\[ p_1(x) = p_0(x) + r_1(x).\]

Polinom \(r_1\) ima stupanj \(\leq 1\). Kako \(p_1\) interpolira \(f\) i u \(x_0\), vrijedi

\[ f_0 = p_1(x_0) = p_0(x_0) + r_1(x_0) = f_0 + r_1(x_0),\]

pa \(r_1\) ima nultočku u \(x_0\):

\[ r_1(x) = a_1(x-x_0),\]

za neki \(a_1 \in \R\). Kako \(p_1\) interpolira \(f\) u \(x_1\), imamo

\[ f_1 = p_1(x_1) = p_0(x_1) + r_1(x_1) = f_0 + r_1(x_1),\]

pa iz \(r_1(x_1) = a_1(x_1 - x_0)\) imamo

\[ a_1 = \frac{f_1 - f_0}{x_1 - x_0}.\]

Dodajmo još jedan čvor interpolacije \(x_2\). Polinom \(p_2\) dobivamo korekcijom iz \(p_1\):

\[ p_2(x) = p_1(x) + r_2(x),\]

gdje je \(r_2\) stupnja \(\leq 2\). Kako \(p_2\) interpolira \(f\) u \(x_0\) i \(x_1\), kao i ranije dobivamo da su \(x_0\) i \(x_1\) nultočke od \(r_2\), koji stoga ima oblik

\[ r_2(x) = a_2(x-x_0)(x-x_1),\]

za neki \(a_2 \in \R\) koji onda možemo odrediti iz uvjeta \(p_2(x_2) = f_2\).

Sada je jasno da će u nastavku konstrukcije korekcije uvijek imati nultočke u svim ranijim čvorovima, a da ćemo vodeći koeficijent u korekciji moći odrediti iz uvjeta interpolacije u novom čvoru. Tako dobivamo interpolacijski polinom u obliku

(3.5)#\[ p_n(x) = a_0 + a_1(x-x_0) + \ldots + a_n \prod_{k=0}^{n-1}(x-x_k),\]

zapisan u Newtonovoj bazi za \(\mathcal{P}_n\) koju čine polinomi

(3.6)#\[ 1, \; x-x_0, \; (x-x_0)(x-x_1), \; \ldots, \; \prod_{k=0}^{n-1} (x-x_k).\]

Potrebno je još samo odrediti koeficijente \(a_0, a_1, \ldots, a_n\). Iz naše konstrukcije je jasno da \(a_k\) ovisi samo o čvorovima \(x_0, \ldots, x_{k}\) i pripadnim funkcijskim vrijednostima \(f_0, \ldots, f_k\). Uvodimo specijalnu oznaku kojom naznačavamo tu ovisnost.

Definicija 3.7 (Podijeljena razlika)

Koeficijent \(a_k\) u prikazu (3.5) interpolacijskog polinoma za funkciju \(f\) u Newtonovoj bazi (3.6) zovemo \(k\)-ta podijeljena razlika ili podijeljena razlika reda \(k\) s čvorovima \(x_0, \ldots, x_k\) i označavamo sa

\[ a_k =: f[x_0, \ldots, x_k], \quad k = 0, \ldots, n.\]

Sada ćemo izvesti rekurzivnu formulu kojom podijeljenu razliku reda \(k\) možemo prikazati pomoću dvije podijeljene razlike reda \((k-1)\). Ta formula će omogućiti vrlo jednostavno računanje koeficijenata u (3.5).

Lema 3.8

Za međusobno različite čvorove \(x_0, \ldots, x_n\), podijeljena razlika \(f[x_0, \ldots, x_n]\) ne ovisi o permutaciji čvorova, tj. za svaku permutaciju \(\sigma\) vrijedi

\[ f[x_0, \ldots, x_n] = f[x_{\sigma(0)}, \ldots, x_{\sigma(n)}].\]
Dokaz.

Označimo sa:

  • \(a_0, \ldots, a_n\) koeficijente interpolacijskog polinoma u Newtonovoj bazi u kojoj čvorove dodajemo redom \(x_0, \ldots, x_n\);

  • \(b_0, \ldots, b_n\) koeficijente tog istog interpolacijskog polinoma u Newtonovoj bazi u kojoj čvorove dodajemo redom \(x_{\sigma(0)}, \ldots, x_{\sigma(n)}\).

Dakle,

\[\begin{split}\begin{align*} p_n(x) &= a_0 + a_1 (x-x_0) + \ldots + a_n \prod_{k=0}^{n-1}(x-x_k) \\ &= b_0 + b_1 (x-x_{\sigma(0)}) + \ldots + b_n \prod_{k=0}^{n-1}(x-x_{\sigma(k)}). \end{align*}\end{split}\]

Koeficijenti u oba prikaza uz odgovarajuće potencije od \(x\) moraju biti jednake. Izjednačavanjem koeficijenata uz \(x^n\) slijedi \(a_n = b_n\), a oni su po definiciji upravo podijeljene razlike iz iskaza Leme.

Lema 3.9

Za podijeljene razlike vrijedi sljedeća rekurzivna formula:

\[ f[x_0, \ldots, x_n] = \frac{f[x_1, \ldots, x_n] - f[x_0, \ldots, x_{n-1}]}{x_n - x_0},\]

pri čemu je \(f[x_k] = f_k\).

Dokaz.

Slično kao u prethodnoj Lemi, označimo sa:

  • \(a_0, \ldots, a_n\) koeficijente interpolacijskog polinoma u Newtonovoj bazi u kojoj čvorove dodajemo redom \(x_0, \ldots, x_n\);

  • \(b_0, \ldots, b_n\) koeficijente tog istog interpolacijskog polinoma u Newtonovoj bazi u kojoj čvorove dodajemo redom \(x_n, \ldots, x_0\).

Dakle,

\[\begin{split}\begin{align*} p_n(x) &= a_0 + a_1 (x-x_0) + \ldots + a_{n-1} \prod_{k=0}^{n-2}(x-x_k) + a_n \prod_{k=0}^{n-1}(x-x_k) \\ &= b_0 + b_1 (x-x_n) + \ldots + b_{n-1} \prod_{k=2}^{n}(x-x_k) + b_n \prod_{k=1}^{n}(x-x_k). \end{align*}\end{split}\]

U prethodnoj Lemi smo dokazali da je \(a_n = b_n\). Izjednačimo sada koeficijente uz \(x^{n-1}\); on se javlja u zadnja dva pribrojnika u oba gornja prikaza:

  • U predzadnjem pribrojniku taj koeficijent je \(a_{n-1}\), odnosno, \(b_{n-1}\).

  • U zadnjem pribrojniku se pojavljuje kada u točno jednoj od zagrada uzmemo \(-x_k\), a u svim preostalim zagradama \(x\).

Izjednačavanjem koeficijenata dobivamo:

\[ a_{n-1} - a_n \sum_{k=0}^{n-1} x_k = b_{n-1} - b_n \sum_{k=1}^{n} x_k.\]

Iskoristimo \(a_n = b_n\) i pokratimo sve \(x_k\) koji se pojavljuju na obje strane u gornjoj jednakosti. Preostaje

\[ a_{n-1} - a_n x_0 = b_{n-1} - a_n x_n,\]

iz čega možemo izraziti \(a_n\):

\[ a_n = \frac{b_{n-1} - a_{n-1} }{x_n - x_0}.\]

Tvrdnja slijedi kada uočimo da je

\[\begin{split}\begin{align*} a_n &= f[x_0, \ldots, x_n], \\ a_{n-1} &= f[x_0, \ldots, x_{n-1}], \\ b_{n-1} &= f[x_n, \ldots, x_1] = f[x_1, \ldots, x_n], \end{align*}\end{split}\]

gdje smo za zadnju jednakost iskoristili prethodnu Lemu.

Kako bismo izračunali sve koeficijente potrebne za prikaz interpolacijskog polinoma u Newtonovoj bazi, popunjavamo sljedeću tablicu.

\[\begin{split}\begin{array}{c|ccccc} x_k & f[x_k] & f[x_k, x_{k+1}] & f[x_k, x_{k+1}, x_{k+2}] & \ldots & f[x_0, \ldots, x_n] \\ \hline x_0 & \red{f[x_0]} & & & & \\ & & \red{f[x_0, x_1]} & & & \\ x_1 & f[x_1] & & \red{f[x_0, x_1, x_2]} & & \\ & & f[x_1, x_2] & & \ddots & \\ \vdots & \vdots & \vdots & \vdots & & \red{f[x_0, \ldots, x_n]} \\ & & f[x_{n-2}, x_{n-1}] & & \ldots & \\ x_{n-1} & f[x_{n-1}] & & f[x_{n-2}, x_{n-1}, x_{n}] & & \\ & & f[x_{n-1}, x_n] & & & \\ x_n & f[x_n] & & & & \end{array}\end{split}\]

Tablicu popunjavamo stupac po stupac, slijeva na desno. Brojeve u svakom stupcu dobivamo pomoću brojeva iz prethodnog stupca, korištenjem rekurzivne formule iz Leme 3.9. Na kraju su nam potrebni samo brojevi označeni crvenom bojom u tablici – no moramo popuniti cijelu tablicu da bismo odredili te brojeve:

\[\begin{split}\begin{align*} p_n(x) = \red{f[x_0]} & + \red{f[x_0, x_1]}(x-x_0) \\ & + \red{f[x_0, x_1, x_2]}(x-x_0)(x-x_1) + \ldots \\ & + \red{f[x_0, x_1, \ldots, x_n]}(x-x_0)\cdots (x-x_{n-1}). \end{align*}\end{split}\]

Algoritam koji na početku u f[k] ima spremljene vrijednosti \(f[x_k]\), a na kraju u f[k] čuva vrijednosti \(f[x_0, \ldots, x_k]\) je vrlo jednostavan:

n = 40; # n = stupanj polinoma -> broj čvorova = n+1.
x = np.linspace(0, 20*np.pi, n+1);
f = np.sin(x);

for i in range(1, n+1):           # za i = 1, 2, ..., n
    for j in range(n, i-1, -1):   #    za j = n, n-1, ..., i
        f[j] = (f[j] - f[j-1]) / (x[j] - x[j-i]);

U algoritmu u \(i\)-tom koraku vanjske petlje u polje f zapisujemo vrijednosti \((i+1)\)-vog stupca tablice, no vrijednosti na indexima \(0, \ldots, i-1\) u polju f ostavljamo na miru, u njima su već izračunati \(f[x_0], \ldots, f[x_0, \ldots, x_{i-1}]\). Nije potrebno pamtiti cijelu tablicu. Ova pripremna faza ima vremensku složenost \(\bigO(n^2)\). Nakon toga, vrijednost \(p_n(x)\) možemo izračunati u složenosti \(\bigO(n)\) koristeći algoritam sličan Hornerovoj shemi:

def pn(xx, x, f):
    # Vraća vrijednost interpolacijskog polinoma p_n u točki xx.
    # Čvorovi su u polju x, a koeficijenti polinoma u Newtonovoj bazi u polju f.
    n = x.shape[0] - 1; # Stupanj polinoma je za 1 manji od broja čvorova.
    sum = f[n];
    for i in range(n-1, -1, -1):       # za i = n-1, n-2, ..., 0
        sum = sum * (xx-x[i]) + f[i];
    
    return sum;

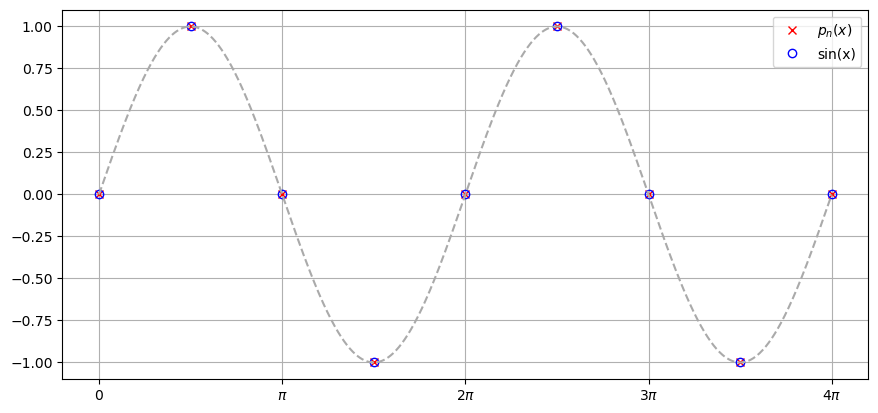
Za razliku od prikaza u kanonskoj bazi, sada nemamo problema s numeričkom nestabilnosti prilikom izvrednjavanja interpolacijskog polinoma i vrijednosti u čvorovima se podudaraju s funkcijskim vrijednostima.

Hide code cell source 
x_first = x[0:9];
plt.figure(figsize=[10.4, 4.8]);
plt.plot(x_first, pn(x_first, x, f), 'rx', label='$p_n(x)$');
plt.plot(x_first, np.sin(x_first), 'bo', label='sin(x)', fillstyle='none');

# Nacrtamo još i graf funkcije sin(x).
x_all = np.linspace(0, 4*np.pi, 1000);
plt.plot(x_all, np.sin(x_all), '--', color='#aaaaaa');

plt.legend();
plt.grid();
plt.xticks(ticks=[0, np.pi, 2*np.pi, 3*np.pi, 4*np.pi], labels=['0', '$\pi$', '2$\pi$', '3$\pi$', '4$\pi$']);
plt.show();
_images/cecbcd27447dfb5b441182b3e1399f78ab4cf9948880c1a21fe75b3ea6ad3f0d.png

Greška interpolacijskog polinoma#

Nakon što odredimo interpolacijski polinom \(p_n\) za zadanu funkciju \(f\), znamo da se vrijednosti od \(p_n\) i od \(f\) podudaraju u čvorovima interpolacije. No možemo li nešto reći o tome koliko dobro \(p_n\) aproksimira \(f\) u točkama koje nisu čvorovi?

Teorem 3.10 (Greška interpolacijskog polinoma)

Pretpostavimo:

  • funkcija \(f\) ima \((n+1)\)-u derivaciju na segmentu \([a, b]\);

  • čvorovi interpolacije \(x_0, \ldots, x_n \in [a, b]\) su međusobno različiti.

Neka je \(p_n\) interpolacijski polinom za \(f\). Tada za svaku točku \(x \in [a, b]\), postoji \(\xi\) takav da je

\[ x_{min} := \min\{x_0, \ldots, x_n, x\} < \xi < \max\{x_0, \ldots, x_n, x\} =: x_{max},\]

te da za grešku interpolacijskog polinoma u točki \(x\) vrijedi

(3.7)#\[ e(x) := f(x) - p_n(x) = \frac{\omega(x)}{(n+1)!} f^{(n+1)}(\xi).\]
Dokaz.

Uočimo da je greška u čvorovima interpolacije jednaka \(e(x_k) = 0\), a da je i desna strana u (3.7) također jednaka \(0\) zbog \(\omega(x_k)=0\). Stoga tvrdnja vrijedi ako je \(x\) čvor interpolacije.

Pretpostavimo dakle da \(x\) nije čvor interpolacije. Tada \(\omega(x) \neq 0\), te iz greške \(e(x)\) „izvucimo” \(\omega(x)\) kao što je napravljeno u (3.7): definirajmo broj \(s(x)\) tako da je

\[ e(x) =: \omega(x) s(x).\]

Za fiksnu vrijednost \(x\), uvedimo funkciju \(g\) koja ovisi o varijabli \(t \in [a, b]\):

\[ g(t) := e(t) - \omega(t)s(x) = e(t) - \omega(t) \frac{e(x)}{\omega(x)} = f(t) - p_n(t) - \omega(t) \frac{e(x)}{\omega(x)}.\]

Uočimo da, kako su \(p_n\) i \(\omega\) polinomi, funkcija \(g\) ima (n+1)-u derivaciju kao i \(f\). Također, čvorovi interpolacije su nultočke od \(g\):

\[ g(x_k) = e(x_k) - \omega(x_k) \frac{e(x)}{\omega(x)} = 0,\]

kao i točka \(x\):

\[ g(x) = e(x) - \omega(x) \frac{e(x)}{\omega(x)} = 0.\]

Dakle, \(g\) ima barem \(n+2\) različite nultočke u \([x_{min}, x_{max}]\). Označimo te nultočke u uzlaznom poretku sa \(y_1 < y_2 < \ldots < y_{n+2}\). Sada primijenimo Rolleov teorem na interval \([y_1, y_2]\): kako je \(g(y_1) = g(y_2)\), postoji \(z_1 \in \langle y_1, y_2 \rangle\) takav da je \(g'(z_1) = 0\). Analogno, primjenom Rolleovog teorema redom na \([y_2, y_3]\), …, \([y_{n+1}, y_{n+2}]\), slijedi da postoje \(z_j \in \langle y_j, y_{j+1} \rangle\) takvi da \(g'(z_j) = 0\), \(j=2, \ldots, n+1\), te je \(z_1 < z_2 < \ldots < z_{n+1}\).

Drugim riječima, \(g'\) ima barem \(n+1\) različitu nultočku u \(\langle x_{min}, x_{max} \rangle\). Induktivnom primjenom Rolleovog teorema, slijedi da \(g''\) ima barem \(n\) nultočki, \(g'''\) ima barem \(n-1\) nultočku, … Na kraju, \(g^{(n+1)}\) ima barem jednu nultočku u \(\langle x_{min}, x_{max} \rangle\). Označimo ju s \(\xi\).

Kako je \(p_n\) polinom stupnja \(\leq n\), vrijedi \(p_n^{(n+1)}(t) = 0\), a kako je \(\omega\) normirani polinom stupnja \(n+1\), vrijedi \(\omega^{(n+1)}(t) = (n+1)!\) za svaki \(t\). Stoga je

\[ g^{(n+1)}(t) = f^{(n+1)}(t) - (n+1)! \frac{e(x)}{\omega(x)},\]

pa uvrštavanjem \(t = \xi\) dobivamo traženi izraz

\[ e(x) = \frac{\omega(x)}{(n+1)!} f^{(n+1)}(\xi).\]

Direktno iz prethodnog teorema možemo dobiti i sljedeću ocjenu za grešku interpolacije.

Korolar 3.11 (Ocjena greške interpolacije polinomom)

Pretpostavimo da je \(f \in C^{n+1}([a, b])\), te označimo \(M_{n+1} := \max_{x \in [a, b]} |f^{(n+1)}(x)|\). Tada za svaki \(x \in [a, b]\) vrijedi:

\[ |f(x) - p_n(x)| \leq \frac{|\omega(x)|}{(n+1)!} M_{n+1}.\]

Korištenjem podijeljenih razlika i zapisa interpolacijskog polinoma u Newtonovoj bazi možemo dobiti još jedan koristan izraz za grešku interpolacije. Uočimo, za razliku od Teorema 3.10, ovdje nemamo pretpostavke na glatkoću funkcije \(f\).

Teorem 3.12 (Greška interpolacijskog polinoma pomoću podijeljenih razlika)

Pretpostavimo:

  • funkcija \(f\) je proizvoljna funkcija na segmentu \([a, b]\);

  • čvorovi interpolacije \(x_0, \ldots, x_n \in [a, b]\) su međusobno različiti.

Neka je \(p_n\) interpolacijski polinom za \(f\). Tada za svaku točku \(x \in [a, b]\) koja nije čvor interpolacije vrijedi

(3.8)#\[ e(x) := f(x) - p_n(x) = \omega(x) f[x_0, \ldots, x_n, x].\]
Dokaz.

U Newtonov oblik polinoma dodajmo još jedan novi čvor \(x_{n+1}\), različit od svih \(x_0, \ldots, x_n\). Dobivamo polinom \(p_{n+1}\) za koji vrijedi:

\[\begin{split} \begin{align*} p_{n+1}(x) &= f[x_0] + f[x_0, x_1](x_1-x_0) + \ldots + f[x_0, \ldots, x_n](x-x_0) \cdots (x-x_{n-1}) \\ & \quad + f[x_0, \ldots, x_n, x_{n+1}] (x-x_0) \cdots (x-x_n) \\ &= p_n(x) + (x-x_0)\cdots(x-x_n) f[x_0, \ldots, x_n, x_{n+1}] \\ &= p_n(x) + \omega(x) f[x_0, \ldots, x_n, x_{n+1}], \end{align*}\end{split}\]

gdje je \(\omega\) polinom čvorova za polazne čvorove \(x_0, \ldots, x_n\) (bez \(x_{n+1}\)). Uvjet interpolacije za polinom \(p_{n+1}\) u novom čvoru \(x_{n+1}\) je

\[ p_{n+1}(x_{n+1}) = f(x_{n+1}),\]

pa uvrštavanjem \(x=x_{n+1}\) gore dobivamo

(3.9)#\[ f(x_{n+1}) - p_n(x_{n+1}) = \omega(x_{n+1}) f[x_0, \ldots, x_n, x_{n+1}].\]

Ovo vrijedi za svaki \(x_{n+1} \in [a, b]\) različit od čvorova \(x_0, \ldots, x_n\), pa obično umjesto \(x_{n+1}\) pišemo samo \(x\) u izrazu (3.9), čime dobivamo tvrdnju iz iskaza teorema.

Usporedimo sada oba izraza za grešku interpolacije:

\[ f_{n+1}(x) - p_n(x) = \omega(x) \frac{f^{n+1}(\xi)}{(n+1)!} = \omega(x) f[x_0, \ldots, x_n, x].\]

Dobili smo sljedeću bitnu tvrdnju o podijeljenim razlikama:

Propozicija 3.13

Neka su zadani čvorovi \(x_0, \ldots, x_n \in [a, b]\). Pretpostavimo da \(f^{(n+1)}\) postoji na cijelom \([a, b]\). Tada za svaku točku \(x \in [a, b]\) postoji \(\xi \in \langle x_{min}, x_{max} \rangle\) takva da vrijedi

\[ f[x_0, \ldots, x_n, x] = \frac{f^{n+1}(\xi)}{(n+1)!}.\]

Ova tvrdnja je poopćenje teorema srednje vrijednosti: kada je \(n=0\), tvrdnja kaže da postoji \(\xi\) takav da vrijedi

\[ f[x, y] = \frac{f(y) - f(x)}{y - x} = f'(\xi).\]

Podijeljene razlike i višestruki čvorovi#

Ako bismo Teorem 3.12 htjeli iskoristiti i u slučaju kada je \(x\) jednak nekom od čvorova, morali bismo definirati značenje izraza \(f[x_0, \ldots, x_n, x]\) kada je \(x = x_k\), odnosno, dopuniti definiciju podijeljene razlike tako da dopušta čvorove koji se pojavljuju više puta. To možemo napraviti proširenjem po neprekidnosti:

\[ f[x_0, x_0] := \lim_{h \to 0} f[x_0, x_0 + h] = \lim_{h \to 0} \frac{f(x_0+h) - f(x_0)}{h} = f'(x_0).\]

Uz ovakvu definiciju, \(f[x_0, x_0]\) je korektno definirana ako i samo ako prva derivacija \(f'\) postoji u točki \(x_0\). Slijedi da tvrdnja Teorema 3.12 vrijedi i kada je \(x = x_k\), za neki čvor \(x_k\), pod pretpostavkom da je \(f'\) definirana u \(x_k\) (naravno, tada je greška jednaka nuli).

Iz gornje diskusije, jasno je da za funkciju dvije varijable

\[\begin{split} f[x, y] = \left\{ \begin{array}{ll} \frac{f(y) - f(x)}{y - x}, & \; x \neq y \\ f'(x), & x = y \end{array}\right.\end{split}\]

vrijedi:

  • \(f\) definirana na \([a, b]\) \(\Rightarrow\) \(f[x, y]\) je definirana na \(S \setminus D\);

  • \(f\) neprekidna na \([a, b]\) \(\Rightarrow\) \(f[x, y]\) je neprekidna na \(S \setminus D\);

  • \(f\) derivabilna na \([a, b]\) \(\Rightarrow\) \(f[x, y]\) je definirana na cijelom \(S\);

  • \(f\) klase \(C^1\) na \([a, b]\) \(\Rightarrow\) \(f[x, y]\) je neprekidna na cijelom \(S\).

Ovdje je \(S = [a, b] \times [a, b]\), a \(D = \{ (x, x) : x \in [a, b] \}\) je njegova dijagonala.

Analogno, po neprekidnosti možemo proširiti definiciju podijeljenih razlika i na slučaj kada se pojavljuje više identičnih čvorova. Uz dovoljnu glatkoću funkcije \(f\), tada vrijedi:

\[ f[x_0, x_1, \ldots, x_n] = \lim_{h_0 \to 0, \ldots, h_n \to 0} f[x_0 + h_0, x_1 + h_1, \ldots, x_n + h_n]\]

i u slučaju kada se neki čvorovi podudaraju. Dovoljna glatkoća znači da, ako se čvor \(x_k\) pojavljuje („ima kratnost”) \(n_k\) puta, onda \(f\) mora biti \(n_k-1\) puta neprekidno derivabilna u \(x_k\). Uz takvu pretpostavku, pokažite za vježbu da vrijede tvrdnje iz sljedeće propozicije.

Propozicija 3.14

Uz pretpostavku o dovoljnoj glatkoći funkcije \(f\) na \([a, b]\), za sve \(x_0, x_1, \ldots, x_n \in [a, b]\) vrijedi:

  1. \(f[x_0, \ldots, x_n]\) je neprekidna na \([a, b] \times [a, b] \times \ldots \times [a, b]\).

  2. \(f[\underbrace{x_0, \ldots, x_0}_{k+1}] = \frac{f^{(k)}(x_0)}{k!}\), za \(k = 0, 1, \ldots\)

  3. Za svaku permutaciju \(\sigma\) vrijedi \(f[x_0, x_1, \ldots, x_n] = f[x_{\sigma(0)}, x_{\sigma(1)}, \ldots, x_{\sigma(n)}]\).

  4. \(f[x_0, x_1, \ldots, x_{n-1}, x_n] = \frac{f[x_1, \ldots, x_n] - f[x_0, \ldots, x_{n-1}]}{x_n - x_0}\), ako je \(x_0 \neq x_n\).

Kasnije će nam trebati i sljedeće činjenice o derivacijama funkcije vezane uz podijeljenu razliku. Lako ih je dokazati korištenjem prethodne propozicije.

Propozicija 3.15

Neka su \(x_0, \ldots, x_n \in [a, b]\) „fiksni” čvorovi, a neka je \(x \in [a, b]\) „varijablni” čvor u podijeljenoj razlici po kojem ju deriviramo. Tada vrijedi:

\[\frac{d}{dx} f[x_0, \ldots, x_n, x] = f[x_0, \ldots, x_n, x, x],\]

te

\[\frac{d}{dx} f[x_0, \ldots, x_n, \underbrace{x, \ldots, x}_k] = k \cdot f[x_0, \ldots, x_n, \underbrace{x, \ldots, x}_k, x].\]
Dokaz.

Dokažimo prvu tvrdnju; druga ide slično.

\[\begin{split} \begin{align*} \frac{d}{dx} f[x_0, \ldots, x_n, x] &= \lim_{h \to 0} \frac{f[x_0, \ldots, x_n, x+h] - f[x_0, \ldots, x_n, x]}{h} \\ &= \lim_{h \to 0} \frac{f[x_0, \ldots, x_n, x+h] - f[x, x_0, \ldots, x_n]}{(x+h) - x} \\ &= \lim_{h \to 0} f[x, x_0, \ldots, x_n, x+h] \\ &= \lim_{h \to 0} f[x_0, \ldots, x_n, x, x+h] \\ &= f[x_0, \ldots, x_n, x, x]. \end{align*} \end{split}\]

Prva jednakost je definicija derivacije, druga i četvrta koriste da se podijeljena razlika ne mijenja permutiranjem čvorova, treća koristi rekurziju za podijeljene razlike, a peta neprekidnost podijeljenih razlika.

Interpolacijski polinom u Pythonu#

U biblioteci scipy.interpolate postoji nekoliko funkcija koje mogu računati vrijednosti interpolacijskog polinoma. Konkretno, poziv funkcije yy = barycentric_interpolate(x, f, xx) će napraviti sljedeće:

  1. Odredit će interpolacijski polinom \(p\) koji u čvorovima x[0], x[1], …, x[n] poprima redom vrijednosti f[0], f[1], …, f[n]. Ovdje je n duljina polja x i f;

  2. Za svaki element polja xx će izračunati vrijednost polinoma \(p\) u toj točki;

  3. Vratit će izračunate vrijednosti interpolacijskog polinoma za elemente od xx redom u polju yy.

Funkcija barycentric_interpolate koristi tzv. baricentrički zapis Lagrangeove forme prilikom izračunavanja \(p\).

from scipy.interpolate import barycentric_interpolate;

# Čvorovi interpolacije: 41 ekvidistantna točka između 0 i 20pi, uključujući rubove.
x = np.linspace(0.0, 20.0*np.pi, num=41);

# Vrijednosti funkcije f u čvorovima interpolacije.
f = np.sin(x);  

# Točke u kojima želimo izračunati vrijednost interpolacijskog polinoma.
# Ovdje uzimamo prvih 9 čvorova interpolacije, no to mogu biti i bilo koje druge točke.
xx = x[0:9];

# Vrijednosti interpolacijskog polinoma pomoću funkcije iz biblioteke scipy.
yy = barycentric_interpolate(x, f, xx);

# Nacrtamo slike kao gore.
plt.figure(figsize=[10.4, 4.8]);
plt.plot(xx, yy, 'rx', label='p(x)');
plt.plot(xx, np.sin(xx), 'bo', label='sin(x)', fillstyle='none');

# Nacrtamo još i graf funkcije sin(x).
x_all = np.linspace(0, 4*np.pi, 1000);
plt.plot(x_all, np.sin(x_all), '--', color='#aaaaaa');

plt.legend();
plt.grid();
plt.xticks(ticks=[0, np.pi, 2*np.pi, 3*np.pi, 4*np.pi], labels=['0', '$\pi$', '2$\pi$', '3$\pi$', '4$\pi$']);
plt.show();
_images/38ca22dc6cdf03d669371c11a034599331ea22cd73ed83b20fb6eb2a4a7189d2.png
Sadržaj