6.1. Rješavanje nelinearnih jednadžbi

Osim (sustava) linearnih jednadžbi, rijetko koju drugu jednadžbu znamo riješiti eksplicitno, tj. egzaktno. Poznate su formule za nalaženje nultočki polinoma stupnja manjeg od 5, dok je za polinome većeg stupnja Galoisova teorija pokazala da je općenito nemoguće dobiti nultočke pomoću konačno mnogo operacija zbrajanja, množenja, dijeljenja i vađenja cjelobrojnih korijena. U srednjoj školi ste rješavali eksponencijalne, logaritamske i trigonometrijske jednadžbe – no te jednadžbe su bile namještene tako da ih je bilo moguće egzaktno riješiti pomoću malog broja poznatih trikova. Na primjer, znamo kako riješiti jednadžbu \(\sin(x) + \cos(x) = 1\), no kako riješiti \(\sin(x) + x\cos(x) = 1\) ili \(\cos(x) + e^x = 1\)?

Općenito, rješavanje bilo koje jednadžbe s jednom nepoznanicom možemo svesti na traženje nultočki neke funkcije.

Definicija 6.1 (Problem rješavanja nelinearne jednadžbe)

Neka je zadana (općenito, nelinearna) funkcija \(f : I \to \R\), gdje je \(I\) neki interval. Tražimo sve one točke \(x \in I\) za koje je

\[ f(x) = 0. \]

Takve točke \(x\) zovu se rješenja ili korijeni pripadne jednadžbe, odnosno, nultočke funkcije \(f\).

Ovdje pretpostavljamo:

• Funkcija \(f\) je neprekidna na \(I\).

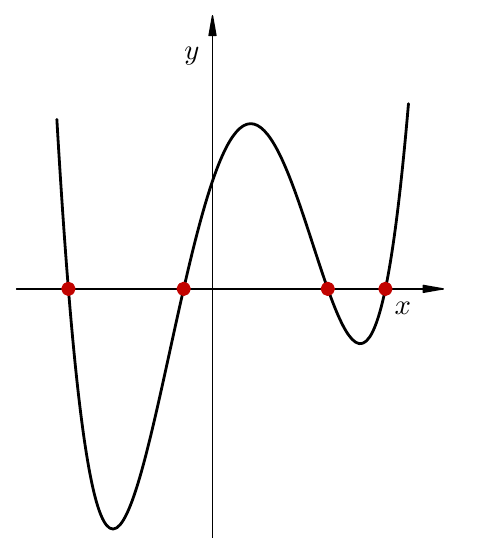
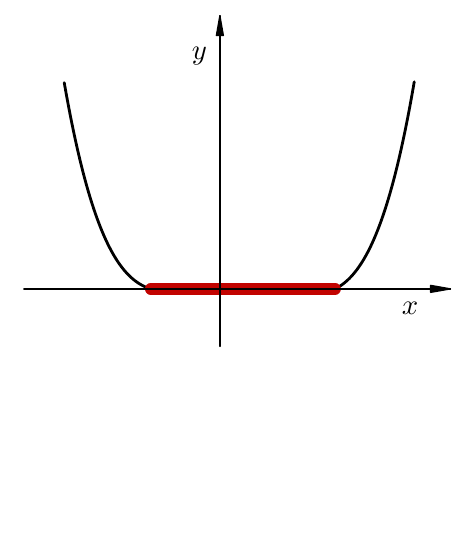
• Nultočke funkcije \(f\) su izolirane.

Kažemo da je nultočka \(\alpha \in I\) funkcije \(f\) izolirana ako postoji okolina od \(\alpha\) u kojoj ne postoji neka druga nultočka od \(f\).

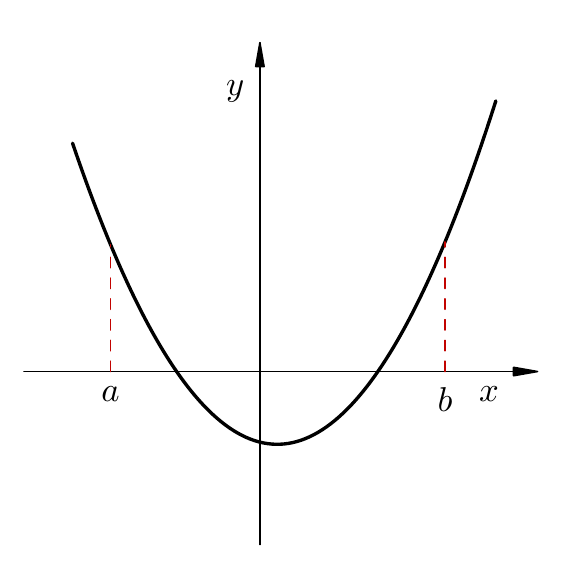
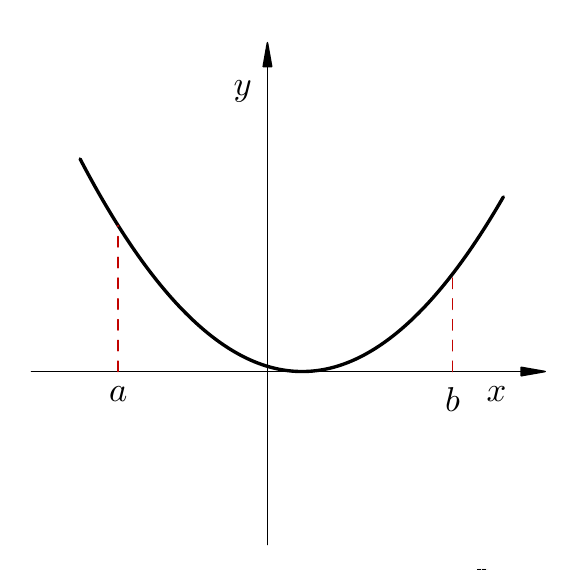
Na slici lijevo, funkcija ima 4 izolirane nultočke. Na slici desno, funkcija ima cijeli interval nultočki; niti jedna od njih nije izolirana.

Neprekidnost funkcije \(f\) obično se koristi pri određivanju intervala u kojem se nalazi nultočka. Naime, ako za neki segment \([a, b]\) vrijedi

(6.1)\[ f(a) \cdot f(b) < 0,\]

a funkcija \(f\) je neprekidna, onda \(f\) nužno ima nultočku unutar \(\langle a, b \rangle\). Naime, tada je ili \(f(a) < 0 < f(b)\) ili je \(f(b) < 0 < f(a)\), a po poznatom rezultatu iz analize, neprekidna funkcija poprima sve međuvrijednosti, pa tako i vrijednost \(f(\alpha) = 0\) za neki \(\alpha \in \langle a, b \rangle\).

Uočimo da se unutar \(\langle a, b \rangle\) može nalaziti i više nultočki funkcije \(f\), kako je vidljivo na donjim slikama. Na obje slike vrijedi \(f(a) \cdot f(b) < 0\), no na slici lijevo je samo jedna nultočka unutar \([a, b]\), dok je na slici desno više nultočki unutar \([a, b]\).

S druge strane, i u segmentu \([a, b]\) za kojeg vrijedi \(f(a) \cdot f(b) > 0\) se mogu (ali ne moraju nužno) nalaziti nultočke od \(f\)! Da bismo ih odredili, morat ćemo dodatno analizirati tok funkcije \(f\) i uzeti manji početni interval. Uočite da na donjoj slici lijevo postoje manji segmenti \([\hat{a}, \hat{b}]\) oko svake od nultočki takvi da vrijedi \(f(\hat{a}) \cdot f(\hat{b}) < 0\). No na slici desno ne možemo pronaći takav interval – takva situacija nastupa kada je nultočka parnog reda. Problem određivanja takvih nultočki je numerički nestabilan: za funkciju \(f\) na slici desno i za po volji mali \(\eps > 0\), funkcija \(f(x) + \eps\) uopće nema nultočku. To nije slučaj niti za sliku lijevo niti za gornje dvije slike.

Napomena

Ako su sve nultočke neprekidne funkcije \(f\) na segmentu \([a, b]\) izolirane, onda tih nultočaka može biti samo konačno mnogo.

U protivnom, postojao bi niz \(\alpha_1, \alpha_2, \ldots\) nultočki unutar \([a, b]\), pa:

• Kako je taj niz ograničen, on ima gomilište \(\alpha \in [a, b]\).

• To gomilište je također nultočka od \(f\) jer je \(f\) neprekidna.

• No u svakoj okolini gomilišta \(\alpha\) tada postoji neki član niza \((\alpha_n)_n\).

• Stoga \(\alpha\) nije izolirana nultočka, što je kontradikcija s pretpostavkom.

Naš cilj je, za zadanu točnost \(\eps > 0\), pronaći aproksimacije \(\hat{\alpha}_1, \hat{\alpha}_2, \ldots, \hat{\alpha}_k\) svih nultočki \(\alpha_1, \alpha_2, \ldots, \alpha_k\) funkcije \(f\) tako da za apsolutnu grešku aproksimacije vrijedi \(|\hat{\alpha}_j - \alpha_j| \leq \eps\). Postupak će se sastojati od dvije faze.

1. Izolacije jedne ili više nultočki: potrebno je pronaći segment \([a, b]\) unutar kojeg se nalazi barem jedna nultočka. Ovo je teži dio posla i obavlja se analizom toka funkcije.

2. Primjena nekog iterativnog algoritma kojim ćemo odrediti nultočku na traženu točnost \(\eps\).

Uočite da će, ponovno zbog Galoisove teorije, svi algoritmi za traženje nultočki nužno morati biti iterativni, a ne konačni! Ti algoritmi će generirati niz sve boljih aproksimacija neke nultočke, a mi ćemo zaustaviti iteracije kada aproksimacija bude zadovoljavajuće točna.

Postoji mnogo metoda za nalaženje nultočaka nelinearnih funkcija na zadanu točnost. Pojedine metode postavljaju i razne dodatne zahtjeve na funkciju \(f\) ili segment \([a, b]\) kako bi dokazivo konvergirale prema nekoj od nultočaka unutar \([a, b]\). Metode razlikujemo i po brzini, tj. redu konvergencije.

Definicija 6.2 (Red konvergencije niza iteracija)

Neka je dan niz iteracija \((x_n)_{n \in \N_0}\) koji konvergira prema \(\alpha \in \R\). Pretpostavimo da je \(p \geq 1\) najveći realni broj za koji postoji konstanta \(c > 0\) takva da vrijedi

\[ |\alpha - x_n| \leq c |\alpha - x_{n-1}|^p, \quad \forall n \in \N. \]

Tada kažemo da niz \((x_n)_n\) konvergira prema \(\alpha\) s redom konvergencije \(p\).

Ako je \(p=1\), kažemo da niz konvergira linearno prema \(\alpha\). U tom slučaju, za faktor linearne konvergencije \(c\) mora vrijediti \(c < 1\).

Ako za \(c < 1\) vrijedi

\[ |\alpha - x_n| \leq c^n |\alpha - x_0|, \quad \forall n \in \N, \]

kažemo da niz \((x_n)_n\) konvergira geometrijski s faktorom \(c\).

Indukcijom je vrlo lako pokazati da, ako niz \((x_n)_n\) konvergira linearno s faktorom \(c\), onda konvergira i geometrijski s istim faktorom. Obrat ne vrijedi, pa zato uvodimo odvojene pojmove.

Metoda bisekcije

Najjednostavnija metoda za nalaženje nultočki je metoda bisekcije. Pretpostavimo da smo, za neprekidnu funkciju \(f\), pronašli interval \([a, b]\) takav da je

\[ f(a) \cdot f(b) < 0. \]

Kako smo već ranije argumentirali, \(f\) tada ima barem jednu nultočku unutar \([a, b]\). Označimo taj početni segment sa \([a_0, b_0] = [a, b]\).

Osnovna ideja metode bisekcije

U segmentu \([a_0, b_0]\) se nalazi neka nultočka funkcije \(f\). Promotrimo njegovo polovište \(x_0 = \frac{a_0+b_0}{2}\). Kako su brojevi \(f(a_0)\) i \(f(b_0)\) različitog predznaka, postoje tri mogućnosti:

1. \(f(x_0) = 0\). Tada je \(x_0\) nultočka od \(f\) i algoritam odmah staje.

2. \(f(x_0)\) i \(f(a_0)\) su različitih predznaka, tj. vrijedi \(f(a_0) \cdot f(x_0) < 0\).

   • Tada \(f\) ima nultočku u \([a_0, x_0]\).

3. \(f(x_0)\) i \(f(b_0)\) su različitih predznaka, tj. vrijedi \(f(x_0) \cdot f(b_0) < 0\).

   • Tada \(f\) ima nultočku u \([x_0, b_0]\).

Ako nismo odmah pronašli nultočku, označimo:

• \([a_1, b_1] := [a_0, x_0]\) ako se dogodio slučaj 2, odnosno,

• \([a_1, b_1] := [x_0, b_0]\) ako se dogodio slučaj 3.

U oba slučaja, širina segmenta se prepolovila, a kako vrijedi \(f(a_1) \cdot f(b_1) < 0\), u \([a_1, b_1]\) se nalazi nultočka funkcije \(f\)!

Ponavljanjem ovog postupka tako dobivamo niz sve manjih segmenata \([a_n, b_n]\), \(n \in \N\) i njihovih polovišta \(x_n = \frac{a_n + b_n}{2}\). Znamo da se u svakom segmentu nalazi neka nultočka funkcije \(f\) jer uvijek osiguravamo da vrijedi \(f(a_n) \cdot f(b_n) < 0\).

Proceduru zaustavljamo kada širina segmenta postane manja od \(\eps\). Polovište tog zadnjeg segmenta će biti naša aproksimacija nultočke; ta aproksimacija je očito udaljena za manje od \(\eps\) od nultočke!

Opisani postupak nazivamo metoda bisekcije ili metoda raspolavljanja. Napišimo pripadni algoritam u Pythonu.

def bisekcija( f, a, b, eps ):
# Ulaz:
#   f - funkcija čiju nultočku tražimo.
#   a, b - brojevi takvi da je f(a)*f(b) < 0.
#   eps - željena točnost aproksimacije.
# Izlaz:
#   x - jedna od nultočki funkcije f unutar [a, b], izračunata s aps. greškom < eps

    fa = f(a); fb = f(b);

    # Ponavljamo sve dok je širina segmenta [a, b] veća od eps.
    while( b - a > eps ):
        # Odredimo polovište trenutnog segmenta.
        x = (a + b) / 2;

        fx = f(x);
        if( fx == 0 ):
            # Možda smo pogodili direktno u nultočku. Vrlo malo vjerojatno.
            return x;
        elif( fa*fx < 0 ):
            # Unutar [a, x] je nultočka -> to postaje novi [a, b].
            b = x; fb = fx;
        else: 
            # Vrijedi fx*fb < 0.
            # Unutar [x, b] je nultočka -> to postaje novi [a, b].
            a = x; fa = fx;

    return x;

Propozicija 6.3 (Konvergencija metode bisekcije)

Neka je \((x_n)_n\) niz polovišta generiran metodom bisekcije za funkciju \(f\) i početni segment \([a, b]\). Tada postoji neka nultočka \(\alpha\) od \(f\) takva da je

\[ \lim_n x_n = \alpha. \]

Za tu nultočku, te svaki \(n \in \N\) vrijedi sljedeća ocjena greške:

\[ |\alpha - x_n| \leq \frac{1}{2^{n+1}} (b-a). \]

Dokaz.

Iako smo već u konstrukciji praktički napravili i dokaz ove propozicije, istaknimo neke detalje: obratit ćemo pažnju na to kojoj nultočki ovaj niz konvergira.

Kako smo ranije spomenuli, funkcija \(f\) unutar segmenta \([a, b]\) može imati samo konačno mnogo nultočki: neka su to \(\alpha_1 < \alpha_2 < \ldots < \alpha_k\). Označimo s \(\delta = \min_{i=2, \ldots, k} |\alpha_i - \alpha_{i-1}|\) najmanji razmak između susjednih nultočaka. Očito, u svakom od intervala \(\langle \alpha_i - \delta, \alpha_i + \delta \rangle\) se nalazi samo jedna nultočka, \(\alpha_i\).

Neka je \(N \in \N\) takav da je \(\frac{1}{2^N}(b-a) < \delta\). U svakom segmentu \([a_n, b_n]\) kojeg generira metoda bisekcije se nalazi bar jedna nultočka; označimo sa \(\alpha_\ast\) bilo koju od nultočki koja je unutar \([a_N, b_N]\). Širina segmenta \([a_N, b_N]\) je jednaka upravo \(\frac{1}{2^N}(b-a) < \delta\), pa vrijedi \([a_N, b_N] \subseteq \langle \alpha_\ast - \delta, \alpha_\ast + \delta \rangle\). Stoga se unutar \([a_N, b_N]\) nalazi samo jedna nultočka, \(\alpha_\ast\).

Kako je \([a_{k+1}, b_{k+1}] \subseteq [a_k, b_k]\), za svaki \(n \geq N\) je upravo \(\alpha_\ast\) jedina nultočka od \(f\) koja je unutar \([a_n, b_n]\). Dodatno, vrijedi

\[ a_0 \leq a_1 \leq \ldots \leq a_n \leq \ldots \leq \alpha_\ast \leq \ldots \leq b_n \leq \ldots \leq b_1 \leq b_0. \]

Stoga po teoremu o sendviču vrijedi \(\lim_n a_n \leq \alpha_\ast \leq \lim_n b_n\). Kako je \(b_n - a_n = \frac{1}{2^n}(b-a)\), imamo \(\lim_n a_n = \lim_n b_n = \alpha_\ast\), pa onda i \(\lim_n x_n = \lim_n \frac{a_n + b_n}{2} = \alpha_\ast\).

Kako je \(\alpha_\ast \in [a_n, b_n]\) za sve \(n \in \N\), a \(x_n\) je polovište od \([a_n, b_n]\), imamo

\[ |\alpha_\ast - x_n| \leq \frac{1}{2}(b_n - a_n) = \frac{1}{2^{n+1}}(b-a). \]

Ocjena greške iz gornje propozicije podsjeća na geometrijsku konvergenciju s faktorom \(c = 1/2\), no zdesna se ne pojavljuje član \(|\alpha - x_0|\). Iz te ocjene možemo unaprijed odrediti koliko je koraka potrebno da pronađemo nultočku sa zadanom točnosti \(\eps > 0\): kako bismo osigurali da vrijedi \(|\alpha - x_n| \leq \eps\), dovoljno je zahtijevati

\[ \frac{1}{2^{n+1}}(b-a) \leq \eps. \]

Sada logaritmiranjem (u bilo kojoj bazi) lako dobivamo da je potreban broj koraka

\[ n \geq \frac{\log(\frac{b-a}{\eps})}{\log 2} - 1. \]

Ako je funkcija \(f\) klase \(C^1\), postoji još jedan, tzv. dinamički kriterij zaustavljanja. Ovaj kriterij je neovisan o metodi, tj. funkcionira za bilo koju metodu, a ne samo za bisekciju.

Propozicija 6.4 (Dinamička ocjena greške)

Neka je \(f \in C^1([a, b])\), \(\alpha \in [a, b]\) bilo koja nultočka funkcije \(f\) te

\[ m_1 = \min_{x \in [a, b]} |f'(x)|. \]

Ako je \(m_1 > 0\), onda za svaki \(x \in [a, b]\) vrijedi

\[ |\alpha - x| \leq \frac{|f(x)|}{m_1}. \]

Dokaz.

Po Teoremu srednje vrijednosti za funkciju \(f\) oko točke \(\alpha\), postoji neki \(\xi\) između \(x\) i \(\alpha\) takav da vrijedi:

\[ f(x) = f(\alpha) + f'(\xi) (x - \alpha). \]

Kako je \(f(\alpha) = 0\), imamo

\[ |x - \alpha| = \frac{|f(x)|}{|f'(\xi)|} \leq \frac{|f(x)|}{m_1}. \]

Uočimo da je \(|f'(\xi)| \geq m_1 > 0\), pa smo smjeli podijeliti sa \(f'(\xi) \neq 0\).

Dinamički kriterij zaustavljanja

Metodu bisekcije (ili bilo koju drugu metodu) možemo zaustaviti kada za aproksimaciju \(x_n\) vrijedi

\[ |f(x_n)| \leq m_1 \eps. \]

Naime, tada iz gornje propozicije direktno slijedi

\[ |\alpha - x_n| \leq \frac{|f(x_n)|}{m_1} \leq \eps. \]

Uočimo da je za dinamički kriterij zaustavljanja potrebno odrediti broj \(m_1 = \min_{x \in [a, b]}|f'(x)|\), što nije uvijek moguće ili jednostavno.

Napomena

Zahtjev \(m_1 > 0\) je iznenađujuće jaki zahtjev na segment \([a, b]\).

Naime, zbog neprekidnosti funkcije \(f'\) iz \(m_1 = \min_{x \in [a, b]}|f'(x)| > 0\) slijedi da \(f'\) ima konstantni predznak na \([a, b]\). Dakle, ili je \(f'(x) > 0\) za sve \(x \in [a, b]\) ili je \(f'(x) < 0\) za sve \(x \in [a, b]\).

To pak povlači da je funkcija \(f\) monotona na \([a, b]\)! Dodatno, zbog monotonosti \(f\) može imati samo jednu nultočku unutar \([a, b]\)!

Newtonova metoda

Newtonova metoda je vjerojatno najvažnija i najčešće korištena metoda za rješavanje nelinearnih jednadžbi. Kao i u ranijim poglavljima, aproksimaciju rješenja za neku „kompliciranu” funkciju \(f\) možemo dobiti tako da \(f\) zamijenimo s nekom jednostavnijom funkcijom. U ovom slučaju, to će biti najjednostavnija moguća funkcija - pravac.

Ideja Newtonove metode

Neka je \(f\) funkcija klase \(C^1([a, b])\).

Pretpostavimo da imamo aproksimaciju \(x_n\) nultočke funkcije \(f\). Povucimo tangentu na graf funkcije \(f\) u točki \((x_n, f(x_n))\). U točki gdje ta tangenta siječe os \(x\) je nova aproksimacija \(x_{n+1}\).

Drugim riječima, funkciju \(f\) aproksimiramo pravcem.

• Tangenta u točki \((x_n, f(x_n))\) je najbolja linearna aproksimacija funkcije \(f\) u okolini točke \(x_n\).

• Nepoznatu nultočku funkcije \(f\) aproksimiramo nultočkom \(x_{n+1}\) tog pravca.

Ovaj postupak ponavljamo.

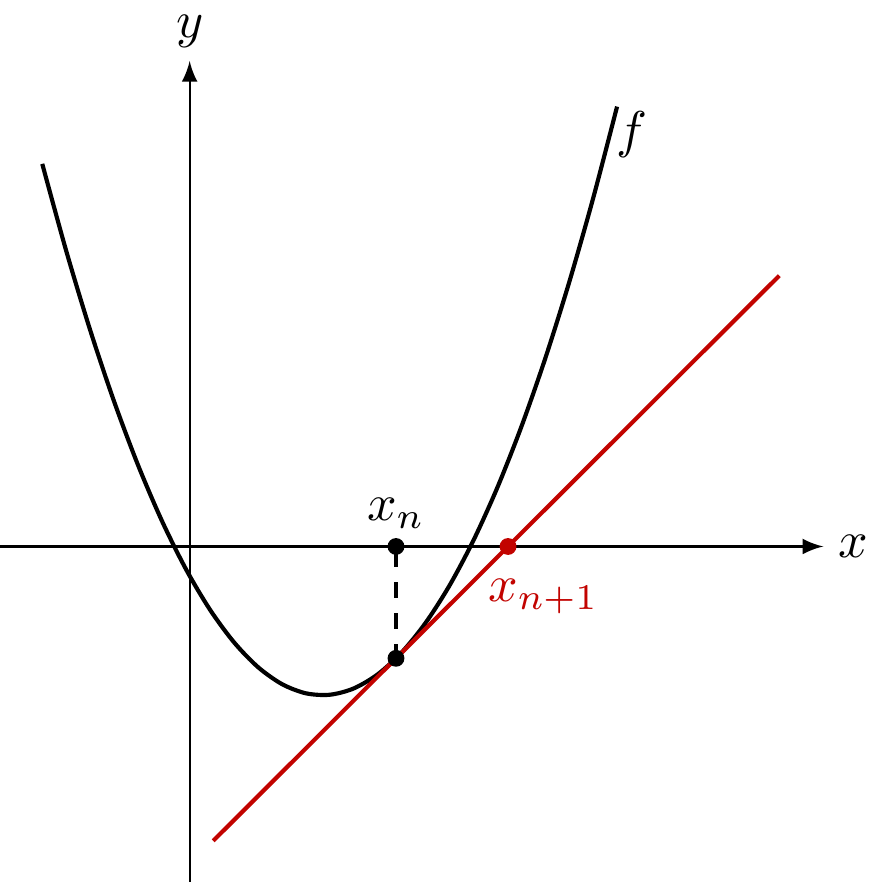
Formulu za iduću iteraciju je lako izvesti: jednadžba tangente funkcije \(f\) u točki \((x_n, f(x_n))\) je

\[ y - f(x_n) = f'(x_n)(x - x_n). \]

Presjek ovog pravca s pravcem \(y=0\) daje točku \(x_{n+1} := x\),

\[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}, \quad n=0, 1, \ldots, \]

pri čemu je \(x_0\) neka pogodno odabrana početna iteracija. Očito, nužan uvjet da bismo izračunali \(x_{n+1}\) jest da vrijedi \(f'(x_n) \neq 0\).

def newton( f, df, x0, eps, max_n ):
# Ulaz:
#   f - funkcija čiju nultočku tražimo.
#   df - derivacija funkcije čiju nultočku tražimo.
#   x0 - početna iteracija
#   max_n - maksimalni broj koraka Newtonove metode.
# Izlaz:
#   x - aproksimacija neke od nultočki funkcije f.

    # Izračunamo max_n koraka Newtonove metode.
    x = x0;
    for n in range( 0, max_n ):
        x = x - f(x) / df(x);

    return x;

Uočite da, za razliku od naše implementacije metode bisekcije, gornja implementacija Newtonove metode nema ugrađeni kriterij zaustavljanja koji bi jamčio točnost nego uvijek izračuna max_n iteracija.

Analiza konvergencije Newtonove metode nije sasvim jednostavna. Ako imamo segment \(I=[a, b]\) unutar kojeg je nultočka \(\alpha\) i početna aproksimacija \(x_0\), onda bez dodatnih pretpostavki

• nije jasno da aproksimacije \(x_n\) ostaju unutar \(I\);

• nije jasno da metoda konvergira prema \(\alpha\) ili čak prema bilo kojoj drugoj nultočki.

Pitanja oko konvergencije niza iteracija prema nultočki

Općenito nas zanimaju tri pitanja vezana uz konvergenciju niza \((x_n)_n\):

1. Brzina konvergencije.

   • Ako niz konvergira prema nultočki, koji je red konvergencije?

2. Lokalna konvergencija.

   • Konvergira li (i pod kojim točno uvjetima) metoda ako je početna točka \(x_0\) dovoljno blizu nultočke \(\alpha\)?

3. Globalna konvergencija.

   • Konvergira li (i pod kojim točno uvjetima) metoda za svaki izbor početne točke \(x_0\) unutar nekog segmenta \(I\)?

Pretpostavimo za početak da niz iteracija konvergira prema nultočki, a kasnije ćemo raspravljati o uvjetima u kojima to vrijedi. Sljedeći teorem pokazuje da će tada konvergencija biti kvadratna, odnosno, bitno brža no kod metode bisekcije.

Teorem 6.5 (Brzina konvergencije Newtonove metode)

Neka je \(f \in C^2(I)\) na nekom segmentu \(I\) koji sadrži jednostruku nultočku \(\alpha\) funkcije \(f\).

Pretpostavimo da niz aproksimacija \((x_n)_n\) generiran Newtonovom metodom konvergira prema \(\alpha\). Tada je brzina konvergencije (barem) kvadratna, te u limesu vrijedi

\[ \lim_n \frac{\alpha - x_{n+1}}{(\alpha - x_n)^2} = \frac{-f''(\alpha)}{2 f'(\alpha)}. \]

Dokaz.

Bez smanjenja općenitosti, možemo pretpostaviti da svi članovi niza \((x_n)_n\) leže unutar segmenta \(I\) (zbog konvergencije prema \(\alpha\), to će se dogoditi počevši od neke iteracije nadalje). Promotrimo Taylorov polinom funkcije \(f\) oko točke \(x_n\):

\[ f(x) = f(x_n) + f'(x_n) (x - x_n) + \frac{f''(\xi_n)}{2}(x - x_n)^2, \]

pri čemu je \(\xi_n \in I\) između \(x\) i \(x_n\). Uvrstimo nultočku \(x = \alpha\), pa dobivamo

\[ 0 = f(\alpha) = f(x_n) + f'(x_n) (\alpha - x_n) + \frac{f''(\xi_n)}{2}(\alpha - x_n)^2, \]

Uz pretpostavku \(f'(x_n) \neq 0\), slijedi

\[ \alpha = \underbrace{x_n - \frac{f(x_n)}{f'(x_n)}}_{x_{n+1}} - \frac{f''(\xi_n)}{2 f'(x_n)} (\alpha - x_n)^2, \]

odnosno,

(6.2)\[ \alpha - x_{n+1} = \frac{-f''(\xi_n)}{2 f'(x_n)} (\alpha - x_n)^2.\]

Po pretpostavci je \(\alpha\) jednostruka nultočka, pa je \(f'(\alpha) \neq 0\).

• Zbog neprekidnosti od \(f'\) slijedi da postoji segment \(I_1 \ni \alpha\) širine veće od nula takav da je \(f'(x) \neq 0\) za svaki \(x \in I_1\).

• Kako \(x_n \to \alpha\), postoji \(N \in \N\) takav da je \(x_n \in I_1\) za sve \(n \geq N\).

• Vrijedi \(\hat{m}_1 := \min_{x \in I_1} |f'(x)| > 0\).

Stavimo

\[ M_2 := \max_{x \in I} |f''(x)|, \quad m_1 := \min\{|f'(x_0)|, \ldots, |f'(x_{N-1})|, \hat{m}_1 \}. \]

Iz (6.2) sada slijedi

\[ |\alpha - x_{n+1}| \leq \frac{M_2}{2m_1} |\alpha - x_n|^2, \]

za sve \(n \in N\), pa je konvergencija kvadratna (reda 2). Dodatno, zapišimo (6.2) malo drugačije:

\[ \frac{\alpha - x_{n+1}}{(\alpha - x_n)^2} = \frac{-f''(\xi_n)}{2 f'(x_n)}. \]

Uočimo da zbog \(\lim_n x_n = \alpha\) i činjenice da je \(\xi_n\) između \(\alpha\) i \(x_n\) slijedi i \(\lim_n \xi_n = \alpha\). Stoga puštanjem limesa u gornjem izrazu dobivamo

\[ \lim_n \frac{\alpha - x_{n+1}}{(\alpha - x_n)^2} = \frac{-f''(\alpha)}{2 f'(\alpha)}. \]

Ovdje smo iskoristili \(f \in C^2(I)\).

Napomena

Primijetimo da iz \( \lim_n \frac{\alpha - x_{n+1}}{(\alpha - x_n)^2} = \frac{-f''(\alpha)}{2 f'(\alpha)} =: C \) slijedi da postoji \(n_1 \in \N\) takav da za sve \(n \geq n_1\) vrijedi

\[ \left| \frac{\alpha - x_{n+1}}{(\alpha - x_n)^2} - C \right| \leq 1, \]

tj. \( \frac{|\alpha - x_{n+1}|}{(\alpha - x_n)^2} \leq 1 + |C|, \) što povlači kvadratnu konvergenciju:

\[ |\alpha - x_{n+1}| \leq (1 + |C|) (\alpha - x_n)^2, \quad n \geq n_1. \]

Općenito, ako pokažemo da postoji \(\lim_n \frac{\alpha - x_{n+1}}{(\alpha - x_n)^p}\) onda niz iteracija ima red konvergencije (barem) \(p\).

Napomena

Taylorov razvoj oko \(x_n\) iz dokaza teorema nam daje i posve analitičku motivaciju za izvod Newtonove metode. Naime, ako je \(x_n \approx \alpha\) dobra aproksimacija, tj. ako je \(|\alpha - x_n| = \eps \ll 1\), onda je \((\alpha - x_n)^2 = \eps^2\) još puno manji, pa u Taylorovom razvoju

\[ \alpha = x_n - \frac{f(x_n)}{f'(x_n)} - \frac{f''(\xi_n)}{2 f'(x_n)} (\alpha - x_n)^2 \]

možemo zanemariti kvadratni član. Time dobivamo

\[ \alpha \approx x_n - \frac{f(x_n)}{f'(x_n)}, \]

što motivira definiciju iduće, bolje aproksimacije upravo formulom \(x_{n+1} := x_n - \frac{f(x_n)}{f'(x_n)}\).

Pokažimo sada da Newtonove iteracije konvergiraju prema jednostrukoj nultočki funkcije \(f \in C^2\) ako je početna iteracija dovoljno blizu te nultočke. Uočite da je ovdje jedini zahtjev na funkciju \(f\) da je ona klase \(C^2\) na bilo kojem segmentu unutar kojeg je nultočka, što je vrlo slabi zahtjev.

Teorem 6.6 (Lokalna konvergencija Newtonove metode)

Neka je \(\alpha\) jednostruka nultočka funkcije \(f \in C^2([a, b])\). Tada postoji \(\eps > 0\) sa svojstvom: ako je

\[ |\alpha - x_0| < \eps, \]

onda niz Newtonovih iteracija \((x_n)_n\) konvergira prema \(\alpha\).

Dokaz.

Kako smo već komentirali kod metode bisekcije, ako je \(\alpha\) jednostruka nultočka, onda zbog \(f'(\alpha) \neq 0\) i neprekidnosti od \(f'\) postoji \(\hat{\eps} > 0\) takav da je \(f'(x) \neq 0\) za sve \(x \in I := [\alpha - \hat{\eps}, \alpha + \hat{\eps}]\). Stavimo

\[ m_1 = \min_{x \in I} |f'(x)| > 0, \quad M_2 = \max_{x \in I} |f''(x)|. \]

Pokažimo da tvrdnja teorema vrijedi za \(\eps := \min\left\{ \frac{m_1}{M_2}, \hat{\eps} \right\}\); ako je \(M_2 = 0\), stavimo \(\eps = \hat{\eps}\).

Označimo još \(q = \frac{M_2}{2m_1}\eps\); očito je \(q \leq \frac{1}{2}\).

Pretpostavimo da je \(|\alpha - x_n| < \eps\) i pokažimo da tada slijedi \(|\alpha - x_{n+1}| \leq q |\alpha - x_n|\). Prisjetimo se izraza (6.2):

\[ \alpha - x_{n+1} = \frac{-f''(\xi_n)}{2 f'(x_n)} (\alpha - x_n)^2, \]

za neki \(\xi_n\) između \(x_n\) i \(\alpha\), tj. za neki \(\xi_n \in I\). Uzimanjem apsolutne vrijednosti imamo

\[\begin{split} \begin{align*} |\alpha - x_{n+1}| &= \frac{|f''(\xi_n)|}{2 |f'(x_n)|} |\alpha - x_n| \cdot |\alpha - x_n| \\ &\leq \frac{M_2}{2 m_1} \eps |\alpha - x_n| \\ &= q |\alpha - x_n|. \end{align*} \end{split}\]

Ako je \(M_2 = 0\), onda je i \(f''(\xi_n) = 0\), pa vrijedi ista ocjena \(|\alpha - x_{n+1}| = 0 \leq q |\alpha - x_n|\).

Specijalno je i \(|\alpha - x_{n+1}| < \eps\). Stoga indukcijom odmah slijedi

\[ |\alpha - x_n| \leq q^n |\alpha - x_0| \to 0, \quad \text{ kada } n \to \infty, \]

jer je \(q < 1\).

U praksi je obično teško iskoristiti tehniku iz dokaza gornjeg teorema kako bismo osigurali konvergenciju Newtonove metode, te nalaženje dobre početne iteracije \(x_0\) može biti netrivijalni problem. S druge strane, ako zahtjevu o tome da \(f'\) ima konstantni predznak na \([a, b]\) dodamo i identični zahtjev na \(f''\), dobivamo globalnu konvergenciju.

Teorem 6.7 (Globalna konvergencija Newtonove metode)

Neka je \(f \in C^2([a, b])\), te neka je \(f(a) \cdot f(b) < 0\).

Dodatno, pretpostavimo da niti \(f'\) niti \(f''\) nemaju nultočku u \([a, b]\).

Tada niz iteracija \((x_n)_n\) generiran Newtonovom metodom konvergira prema jedinstvenoj jednostrukoj nultočki \(\alpha \in [a, b]\) za svaku početnu iteraciju \(x_0 \in [a, b]\) za koju vrijedi

\[ f(x_0) \cdot f''(x_0) > 0. \]

Dokaz.

Kako \(f'\) i \(f''\) nemaju nultočku u \([a, b]\), a neprekidne su, obje te funkcije su konstantnog predznaka na \([a, b]\). Promotrimo samo jedan od četiri moguća slučaja za te predznake; u ostalim slučajevima dokaz ide posve analogno.

Pretpostavimo da je \(f'(x) > 0\) i \(f''(x) > 0\) za sve \(x \in [a, b]\).

• Dakle, funkcija \(f\) je monotono rastuća i konveksna na \([a, b]\).

• Stoga je \(f(a) < 0\) i \(f(b) > 0\).

• Zbog \(f''(x_0) > 0\) i pretpostavke teorema, vrijedi \(f(x_0) > 0\).

• Kako je \(f\) rastuća, slijedi \(x_0 > \alpha\).

Pokažimo indukcijom da vrijedi \(\alpha < x_n \leq x_0\), za sve \(n \in \N_0\); bazu smo već pokazali.

• Za korak indukcije, pretpostavimo \(\alpha < x_n \leq x_0\).

• Tada \(0 = f(\alpha) < f(x_n)\) jer je \(f\) rastuća.

• Stoga

  \[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} < x_n.\]

  pa niz \((x_n)_n\) monotono pada.

• Iz Taylorove formule oko \(x_n\) je

  \[ 0 = f(\alpha) = f(x_n) + f'(x_n)(\alpha - x_n) + \frac{f''(\xi_n)}{2} (\alpha - x_n)^2,\]

  za \(\xi_n \in \langle \alpha, x_n \rangle \subseteq [a, b]\). Stoga \(f''(\xi_n) > 0\), pa je

  \[ f(x_n) + f'(x_n) (\alpha - x_n) < 0,\]

  odakle slijedi

  \[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} > \alpha.\]

Dakle, niz \((x_n)_n\) je odozdo ograničen s \(\alpha\) i monotono pada, pa postoji limes

\[ \hat{\alpha} := \lim_n x_n \]

za koji vrijedi \(\alpha \leq \hat{\alpha} \leq x_0\), tj. \(\hat{\alpha} \in [a, b]\). Puštanjem limesa \(n \to \infty\) u formuli \(x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\) slijedi

\[ \hat{\alpha} = \hat{\alpha} - \frac{f(\hat{\alpha})}{f'(\hat{\alpha})}. \]

Uočimo da je \(f'(\hat{\alpha}) \neq 0\) jer \(\hat{\alpha} \in [a, b]\). Stoga slijedi \(f(\hat{\alpha}) = 0\). Kako \(f\) ima jedinstvenu nultočku \(\alpha \in [a, b]\), mora biti \(\hat{\alpha} = \alpha\).

Rub intervala je dobra početna točka

Iz pretpostavke da \(f''\) ima konstantni predznak na \([a, b]\) te zbog \(f(a)f(b) < 0\) slijedi da u prethodnom teoremu uvijek možemo uzeti ili \(x_0 = a\) ili \(x_0 = b\).

Izvedimo još za kraj ove cjeline jedan kriterij zaustavljanja Newtonove metode pomoću kojeg ćemo detektirati kada je aproksimacija zadovoljavajuće točna.

Propozicija 6.8

Pretpostavimo da funkcija \(f \in C^2([a, b])\) ima nultočku \(\alpha \in [a, b]\) te da sve iteracije \(x_n\) generirane Newtonovom metodom leže unutar intervala \([a, b]\). Tada vrijedi

\[ |\alpha - x_n| \leq \frac{M_2}{2m_1} (x_n - x_{n-1})^2. \]

Dokaz.

Promotrimo Taylorov polinom za \(f\), ovog puta oko točke \(x_{n-1}\), te uvrstimo \(x = x_n\):

\[ f(x_n) = f(x_{n-1}) + f'(x_{n-1})(x_n - x_{n-1}) + \frac{f''(\xi_{n-1})}{2} (x_n - x_{n-1})^2, \]

pri čemu je \(\xi_{n-1}\) između \(x_{n-1}\) i \(x_n\), dakle, ponovno unutar \([a, b]\). Po definiciji iteracija u Newtonovoj metodi, vrijedi \(f(x_{n-1}) + f'(x_{n-1})(x_n - x_{n-1}) = 0\), pa je

\[ f(x_n) = \frac{f''(\xi_{n-1})}{2} (x_n - x_{n-1})^2, \]

odnosno,

\[ |f(x_n)| \leq \frac{M_2}{2} (x_n - x_{n-1})^2. \]

Sada iskoristimo dinamičku ocjenu greške (Propozicija 6.4):

\[ |\alpha - x_n| \leq \frac{|f(x_n)|}{m_1} \leq \frac{M_2}{2m_1} (x_n - x_{n-1})^2. \]

Pomoću gornje propozicije možemo izvesti kriterij za zaustavljanje Newtonove metode: ako želimo dobiti aproksimaciju nultočke tako da apsolutna greška bude manja od \(\eps\), iteracije ćemo zaustaviti kada je

\[ |x_n - x_{n-1}| \leq \sqrt{\frac{2m_1}{M_2} \eps}. \]

Naravno, i dalje možemo koristiti i raniji dinamički kriterij zaustavljanja

\[ |f(x_n)| \leq m_1 \eps. \]

Metoda jednostavnih iteracija

Još jednu tehniku za rješavanje nelinearnih jednadžbi, ali i za analizu drugih metoda možemo dobiti tako da transformiramo originalnu jednadžbu u oblik \(\varphi(x) = x\). Tada točke \(\alpha\) za koje vrijedi \(\varphi(\alpha) = \alpha\) zovemo fiksne točke funkcije \(\varphi\).

Ideja metode jednostavnih iteracija

Neka je \(\alpha\) fiksna točka funkcije \(\varphi\), a \(x_0\) neka početna aproksimacija za \(\alpha\).

Metoda jednostavnih iteracija ili metoda fiksne točke generira niz

\[ x_{n+1} = \varphi(x_n), \quad n \geq 0\dots \]

Promotrimo sada nekoliko primjera kako rješavanje jednadžbe \(f(x) = 0\) možemo transformirati u problem nalaženja fiksne točke \(\varphi(x) = x\) za neku funkciju \(\varphi\).

Primjer 6.9

Reformulirajmo problem računanja \(\sqrt{a}\), tj. rješavanja nelinearne jednadžbe

\[ f(x) = x^2 - a = 0, \quad \text{za } a > 0 \]

u problem nalaženja fiksne točke.

1. pristup. \(x = x^2 + x - a\), tj. tražimo fiksnu točku funkcije \(\varphi(x) = x^2 + x - a\).

2. pristup. \(x = a/x\), tj. tražimo fiksnu točku funkcije \(\varphi(x) = a/x\).

3. pristup. \(x = \frac{1}{2}(x + a/x)\), tj. tražimo fiksnu točku funkcije \(\varphi(x) = \frac{1}{2}(x + a/x)\).

Konvergenciju pripadnih nizova za svaki od ovih pristupa ćemo analizirati kasnije.

Sada ćemo vidjeti pod kojim uvjetima niz generiran metodom jednostavnih iteracija konvergira ka fiksnoj točki. Izvedimo prvo dovoljan uvjet da bi funkcija \(\varphi\) uopće imala fiksnu točku.

Lema 6.10 (Egzistencija fiksne točke)

Neka je funkcija \(\varphi\) neprekidna na \([a, b]\) i neka vrijedi

\[ a \leq \varphi(x) \leq b, \quad \text{za sve } x \in [a, b]. \]

Tada funkcija \(\varphi\) ima barem jednu fiksnu točku \(\alpha \in [a, b]\).

Dokaz.

Promotrimo funkciju \(g(x) := \varphi(x) - x\). Ta funkcija je neprekidna na \([a, b]\) i vrijedi

\[ g(a) = \varphi(a) - a \geq 0, \quad g(b) = \varphi(b) - b \leq 0. \]

Dakle, neprekidna funkcija \(g\) mijenja predznak na \([a, b]\), pa ima nultočku \(\alpha \in [a, b]\). Iz \(g(\alpha) = 0\) slijedi \(f(\alpha) = \alpha\).

Primijetimo da zahtjev

\[ a \leq \varphi(x) \leq b, \quad \text{za sve } x \in [a, b] \]

možemo kompaktnije zapisati kao

\[ \varphi([a, b]) \subseteq [a, b]. \]

Teorem 6.11 (Konvergencija metode jednostavnih iteracija za kontrakciju)

Neka je funkcija \(\varphi\) neprekidna na \([a, b]\) i neka je

\[ \varphi([a, b]) \subseteq [a, b]. \]

Pretpostavimo da je funkcija \(\varphi\) kontrakcija, odnosno, da postoji konstanta \(q \in \langle 0, 1 \rangle\) takva da vrijedi

\[ |\varphi(x) - \varphi(y)| \leq q |x - y|, \quad \text{za sve } x, y \in [a, b], \]

Tada funkcija \(\varphi\) ima jedinstvenu fiksnu točku \(\alpha \in [a, b]\). Nadalje, za proizvoljnu početnu iteraciju \(x_0 \in [a, b]\), niz iteracija

\[ x_{n+1} = \varphi(x_n), \quad n \geq 0 \]

konvergira prema \(\alpha\).

Dokaz.

Iz prethodne leme slijedi da \(\varphi\) ima bar jednu fiksnu točku \(\alpha \in [a, b]\). Pokažimo da je ona jedinstvena.

Pretpostavimo da je \(\beta\) neka druga fiksna točka. Kako vrijedi \(\varphi(\alpha) = \alpha\) i \(\varphi(\beta) = \beta\), slijedi

\[ |\alpha - \beta| = |\varphi(\alpha) - \varphi(\beta)| \leq q|\alpha - \beta|, \]

odnosno \((1-q)|\alpha - \beta| \leq 0\). Zbog \(1 - q > 0\), mora biti \(|\alpha - \beta| \leq 0\), što je moguće jedino ako \(\alpha = \beta\), čime smo pokazali jedinstvenost.

Uzmimo sada proizvoljnu početnu točku \(x_0 \in [a, b]\) za metodu jednostavnih iteracija.

• Iz \(x_{n} \in [a, b]\) slijedi \(x_{n+1} = \varphi(x_n) \in [a, b]\), pa cijeli niz \((x_n)_n\) ostaje unutar \([a, b]\).

• Kako je \(\varphi\) kontrakcija, imamo

  \[ |\alpha - x_{n+1}| = |\varphi(\alpha) - \varphi(x_n)| \leq q |\alpha - x_n|,\]

  pa indukcijom slijedi

  \[ |\alpha - x_n| \leq q^n |\alpha - x_0|, \quad \text{za sve } n \geq 1.\]

• Puštanjem \(n \to \infty\), zbog \(0 < q < 1\) slijedi \(x_n \to \alpha\).

Uočimo da iz relacije \(|\alpha - x_{n+1}| \leq q |\alpha - x_n|\) koju smo imali u dokazu teorema slijedi da metoda jednostavne iteracije konvergira (barem) linearno s faktorom \(q\).

Uz iste pretpostavke koje smo imali u teoremu možemo izvesti ocjenu greške.

Teorem 6.12 (Ocjena greške metode jednostavnih iteracija)

Neka je funkcija \(\varphi \in C([a, b])\) kontrakcija s faktorom \(q < 1\), te neka je

\[ \varphi([a, b]) \subseteq [a, b]. \]

Tada je

\[ |\alpha - x_n| \leq \frac{q^n}{1-q} |x_1 - x_0|, \quad \text{za sve } n \geq 1. \]

Dokaz.

Za dvije susjedne iteracije \(x_n = \varphi(x_{n-1})\) i \(x_{n+1} = \varphi(x_{n})\) vrijedi

\[ |x_{n+1} - x_n| = |\varphi(x_n) - \varphi(x_{n-1})| \leq q|x_n - x_{n-1}|. \]

Induktivnom primjenom ovog argumenta, imamo:

\[ |x_{n+1} - x_n| \leq q|x_n - x_{n-1}| \leq q^2 |x_{n-1} - x_{n-2}| \leq \ldots \leq q^n |x_1 - x_0|. \]

Posve analogno dobili bismo ocjenu \(|x_{n+\ell} - x_{n+\ell-1}| \leq q^\ell |x_{n} - x_{n-1}|\) za bilo koji \(\ell \geq 1\). Pomoću nejednakosti trokuta i ove ocjene dobivamo

\[\begin{split} \begin{align*} |x_{n+p} - x_n| &= |x_{n+p} - x_{n+p-1} + x_{n+p-1} - \cdots - x_{n+1} + x_{n+1} - x_n| \\ &\leq |x_{n+p} - x_{n+p-1}| + \cdots + |x_{n+1} - x_n| \\ &\leq q^p |x_{n} - x_{n-1}| + q^{p-1} |x_{n} - x_{n-1}| + \ldots + q |x_{n} - x_{n-1}| \\ &= q(q^{p-1} + \ldots + 1) |x_{n} - x_{n-1}| \\ &\leq \frac{q}{1-q} |x_{n} - x_{n-1}|. \end{align*} \end{split}\]

Sada pustimo \(p \to \infty\). Zbog prethodnog teorema, vrijedi \(x_{n+p} \to \alpha\), gdje je \(\alpha\) jedinstvena fiksna točka od \(\varphi\). Ostali članovi nejednakosti ne ovise o \(p\), pa u limesu vrijedi

\[ |\alpha - x_n| \leq \frac{q}{1-q} |x_{n} - x_{n-1}| \leq \frac{q^n}{1-q} |x_1 - x_0|. \]

Pri kraju dokaza gornjeg teorema imali smo ocjenu

\[ |\alpha - x_n| \leq \frac{q}{1-q} |x_{n} - x_{n-1}|. \]

Ako želimo pronaći aproksimaciju \(x_n\) čija je apsolutna greška manja od \(\eps\), dovoljno je osigurati da vrijedi

\[ \frac{q}{1-q} |x_{n} - x_{n-1}| \leq \eps. \]

Dakle, dinamički kriterij za zaustavljanje procesa jednostavnih iteracija je

\[ |x_{n} - x_{n-1}| \leq \frac{\eps(1-q)}{q}. \]

Kod jednostavnih iteracija je moguće i unaprijed predvidjeti koliko nam koraka maksimalno treba da bi apsolutna greška bila \(\leq \eps\). Dovoljno je samo izračunati \(x_1\) i znati faktor kontrakcije \(q\), jer je prema gornjem teoremu dovoljno osigurati \(\frac{q^n}{1-q}|x_1 - x_0| \leq \eps\), odnosno

\[ n \geq \frac{\log \frac{\eps(1-q)}{|x_1 - x_0|}}{\log q}. \]

Vratimo se sada na diskusiju o konvergenciji metode jednostavnih iteracija i promotrimo što se događa kada je funkcija \(\varphi \in C^1[(a, b)]\). Označimo, kako i do sada, \(M_1 := \max_{x \in [a, b]}|f'(x)|\). Lako se vidi da je u slučaju \(M_1 < 1\) funkcija \(\varphi\) kontrakcija s faktorom \(M_1\), pa imamo sljedeći korolar.

Korolar 6.13

Neka je \(\varphi \in C^1([a, b])\) takva da je \(\varphi([a, b]) \subseteq [a, b]\). Ako je

\[ q := M_1 = \max_{x \in [a, b]}|f'(x)| < 1, \]

onda jednadžba \(\varphi(x) = x\) ima jedinstveno rješenje \(\alpha \in [a, b]\).

Dodatno, za proizvoljnu početnu točku \(x_0 \in [a, b]\) i niz \((x_n)_n\) generiran metodom jednostavnih iteracija vrijedi:

\[\begin{split} \begin{align*} \lim_n x_n &= \alpha, \\ |\alpha - x_n| &\leq q^n |\alpha - x_0|, \quad \text{za sve } n \geq 0, \\ \lim_n \frac{\alpha - x_{n+1}}{\alpha - x_n} &= \varphi'(\alpha). \end{align*} \end{split}\]

Dokaz.

Po teoremu srednje vrijednosti, za bilo koje \(x, y \in [a, b]\) vrijedi

\[ \varphi(x) - \varphi(y) = \varphi'(\xi) (x - y), \]

za neki \(\xi\) između \(x, y\), tj. za neki \(\xi \in [a, b]\). Uzimanjem apsolutne vrijednosti odmah slijedi da je

\[ |\varphi(x) - \varphi(y)| \leq q |x - y|. \]

Stoga je \(\varphi\) kontrakcija s faktorom \(q = M_1\) i sve tvrdnje korolara osim zadnje slijede direktno iz Teorema 6.11 i ranijih razmatranja.

Zadnju tvrdnju dobijemo tako da ponovno promotrimo teorem srednje vrijednosti:

\[ \alpha - x_{n+1} = \varphi(\alpha) - \varphi(x_n) = \varphi'(\xi_n) (\alpha - x_n), \]

gdje je \(\xi_n\) između \(\alpha\) i \(x_n\). Budući da \(x_n \to \alpha\), vrijedi i \(\xi_n \to \alpha\). Zbog neprekidnosti od \(\varphi'\) tada vrijedi

\[ \lim_n \frac{\alpha - x_{n+1}}{\alpha - x_n} = \lim_n \varphi'(\xi_n) = \varphi'(\alpha). \]

Možemo pokazati čak i više: dovoljno je da samo za fiksnu točku \(\alpha\) vrijedi \(|\varphi'(\alpha)| < 1\) da bi metoda jednostavnih iteracija bila lokalno konvergentna.

Korolar 6.14 (Lokalna konvergencija metode jednostavnih iteracija)

Neka je \(\varphi\) funkcija klase \(C^1\) na nekoj okolini svoje fiksne točke \(\alpha\). Ako je

\[ |\varphi'(\alpha)| < 1 \]

i ako je početna točka \(x_0\) dovoljno blizu \(\alpha\), onda vrijede sve tvrdnje o konvergenciji niza \((x_n)_n\) iz Korolara 6.13.

Dokaz.

Kako je \(|\varphi'(\alpha)| < 1\), onda zbog neprekidnosti od \(\varphi'\) postoji \(\eps > 0\) takav da za segment \(I = [\alpha - \eps, \alpha + \eps]\) vrijedi

\[ \max_{x \in I} |\varphi'(x)| < 1. \]

Stavimo \(q := \max_{x \in I} |\varphi'(x)|\). Neka je \(x \in I\) proizvoljan. Vrijedi \(|\alpha - x| \leq \eps\), pa po teoremu srednje vrijednosti imamo

\[ |\alpha - \varphi(x)| = |\varphi(\alpha) - \varphi(x)| = |\varphi'(\xi) (\alpha - x)| \leq q |\alpha - x| \leq \eps. \]

Stoga je \(\varphi(x) \in I\), odnosno, \(\varphi(I) \subseteq I\) pa možemo primijeniti Korolar 6.13 za segment \([a, b] = I\).

Primijetimo da, ako vrijedi \(|\varphi'(\alpha)| > 1\), onda metoda jednostavnih iteracija neće konvergirati prema \(\alpha\). Naime, tada je i u nekoj okolini od \(\alpha\) derivacija po modulu veća od \(1\), pa čim je \(x_n\) dovoljno blizu \(\alpha\), vrijedi

\[ |\alpha - x_{n+1}| = |\varphi(\alpha) - \varphi(x_n)| = |\varphi'(\xi)| \cdot |\alpha - x_n| > |\alpha - x_n|, \]

tj. iduća iteracija je gora aproksimacija od \(\alpha\) no što je bila \(x_n\)!

Primijenimo sada napokon teoriju koju smo razvili za primjer s računanjem \(\sqrt{a}\).

Primjer 6.15

Ispitajmo konvergenciju sva tri pristupa za računanje \(\sqrt{a}\) metodom jednostavnih iteracija.

1. pristup. Za \(\varphi(x) = x^2 + x - a\) imamo \(\varphi'(x) = 2x+1\). Uvrštavanjem fiksne točke \(x = \alpha = \sqrt{a}\) dobivamo

\[ \varphi'(\sqrt{a}) = 2 \sqrt{a} + 1 > 1, \]

pa metoda jednostavnih iteracija za tu funkciju \(\varphi\) neće konvergirati. Štoviše, za bilo koju početnu točku \(x_0\) ove iteracije divergiraju!

2. pristup. Za \(\varphi(x) = a/x\) imamo \(\varphi'(x) = -a/x^2\). Uvrštavanjem fiksne točke \(x = \alpha = \sqrt{a}\) dobivamo

\[ \varphi'(\sqrt{a}) = -1, \]

pa metoda jednostavnih iteracija za tu funkciju \(\varphi\) neće konvergirati. Niz iteracija je periodički: \(x_0, a/x_0, x_0, a/x_0, \ldots\)

3. pristup. Za \(\varphi(x) = \frac{1}{2}(x + a/x)\) imamo \(\varphi'(x) = \frac{1}{2}(1 - a/x^2)\). Uvrštavanjem fiksne točke \(x = \alpha = \sqrt{a}\) dobivamo

\[ \varphi'(\sqrt{a}) = 0, \]

pa metoda jednostavnih iteracija za tu funkciju \(\varphi\) konvergira u okolini od \(\alpha = \sqrt{a}\). Zanimljivo, ova metoda se podudara upravo s Newtonovom metodom za jednadžbu \(x^2 - a = 0\) i ponekad se još naziva babilonska metoda (iako nema dokaza da su ju poznavali Babilonci).

Red konvergencije metode jednostavnih iteracija može biti i veći od jedan, kako pokazuje sljedeći teorem.

Teorem 6.16 (Iterativne metode višeg reda konvergencije)

Neka je funkcija \(\varphi\) klase \(C^p\) na nekoj okolini svoje fiksne točke \(\alpha\), za neki \(p \geq 2\), te neka vrijedi

\[ \varphi'(\alpha) = \ldots = \varphi^{(p-1)}(\alpha) = 0. \]

Ako je početna točka \(x_0\) dovoljno blizu \(\alpha\), onda niz \((x_n)_n\) generiran metodom jednostavnih iteracija konvergira prema \(\alpha\) s redom konvergencije (barem) \(p\) i vrijedi

\[ \lim_n \frac{\alpha - x_{n+1}}{(\alpha - x_n)^p} = (-1)^{p-1} \frac{\varphi^{(p)}(\alpha)}{p!}. \]

Dokaz.

Promotrimo Taylorov polinom stupnja \(p-1\) za funkciju \(\varphi\) oko \(\alpha\) i uvrstimo \(x = x_n\):

\[\begin{split} \begin{align*} \varphi(x_n) = \varphi(\alpha) &+ \varphi'(\alpha)(x_n - \alpha) + \ldots \\ &+\frac{\varphi^{(p-1)}(\alpha)}{(p-1)!} (x_n - \alpha)^{p-1} + \frac{\varphi^{(p)}(\xi_n)}{p!}(x_n - \alpha)^p, \end{align*} \end{split}\]

za neki \(\xi_n\) između \(x_n\) i \(\alpha\). Sada uvrstimo \(\varphi(\alpha) = \alpha\), \(\varphi(x_n) = x_{n+1}\), te \(\varphi^{(k)}(\alpha) = 0\) za \(k=1, \ldots, p-1\). Slijedi

\[ x_{n+1} = \alpha + \frac{\varphi^{(p)}(\xi_n)}{p!}(x_n - \alpha)^p. \]

Zbog \(|\varphi'(\alpha)| = 0 < 1\), niz iteracija \((x_n)_n\) konvergira prema \(\alpha\) za svaki \(x_0\) koji je dovoljno blizu \(\alpha\). Ponovno, zbog \(x_n \to \alpha\) slijedi i \(\xi_n \to \alpha\). Stoga imamo

\[ \lim_n \frac{\alpha - x_{n+1}}{(\alpha - x_n)^p} = (-1)^{p-1} \lim_n \frac{\varphi^{(p)}(\xi_n)}{p!} = (-1)^{p-1} \frac{\varphi^{(p)}(\alpha)}{p!}. \]

Kako smo i ranije komentirali, iz činjenice da ovaj limes postoji direktno slijedi da je red konvergencije niza \((x_n)_n\) barem \(p\).

Teorem koji smo upravo pokazali je izuzetno koristan i za analizu drugih metoda za rješavanje nelinearnih jednadžbi.

Primjer 6.17

Neka je \(\alpha\) jednostruka nultočka funkcije \(f\). Analizirajmo red konvergencije Newtonove metode u okolini od \(\alpha\). Newtonovu metodu možemo zapisati kao metodu jednostavnih iteracija:

\[ x_{n+1} = \varphi(x_n), \quad \text{gdje je } \varphi(x) = x - \frac{f(x)}{f'(x)}. \]

Promotrimo sada derivaciju funkcije \(\varphi\):

\[ \varphi'(x) = 1 - \frac{(f'(x))^2 - f(x) f''(x)}{(f'(x))^2} = \frac{f(x) f''(x)}{(f'(x))^2}. \]

Kada uvrstimo \(f(\alpha) = 0\), slijedi

\[ \varphi'(\alpha) = 0, \]

pa iz Teorema 6.16 direktno slijedi da je red konvergencije Newtonove metode oko nultočke \(\alpha\) barem 2, tj. metoda konvergira barem kvadratno.

Izračunajmo i drugu derivaciju:

\[ \varphi''(x) = \ldots = \frac{f''(x)}{f'(x)} + f(x) \left( \frac{f''(x)}{(f'(x))^2} \right)'. \]

Zbog \(f(\alpha) = 0\) i \(f'(\alpha) \neq 0\), slijedi

\[ \varphi''(\alpha) = \frac{f''(\alpha)}{f'(\alpha)}. \]

Zaključak:

• Ako je \(f''(\alpha) \neq 0\), red konvergencije Newtonove metode je \(2\).

• Ako je \(f''(\alpha) = 0\), red konvergencije Newtonove metode je barem \(3\).

Newtonova metoda za višestruku nultočku

Uočimo da pomoću Teorema 6.16 možemo analizirati konvergenciju Newtonove metode i u slučaju kada funkcija \(f\) ima višestruku nultočku \(\alpha\).

Konkretno, pretpostavimo da je \(\alpha\) nultočka kratnosti \(m > 1\) funkcije \(f\) koja je klase \(C^{m+1}\) u nekoj okolini od \(\alpha\). Tada je

\[ f(x) = (x - \alpha)^m g(x) \]

za neku funkciju \(g\) klase \(C^1\) na okolini od \(\alpha\) za koju vrijedi \(g(\alpha) \neq 0\). Tada imamo:

\[ f(\alpha) = f'(\alpha) = \ldots = f^{(m-1)}(\alpha) = 0, \quad f^{(m)}(\alpha) \neq 0. \]

te \(f'(x) = m (x-\alpha)^{m-1} g(x) + (x-\alpha)^m g'(x) = (x - \alpha)^{m-1} g_1(x)\) za \(g_1(x) = m g(x) + (x - \alpha) g'(x)\). Iteracijska funkcija kod Newtonove metode je

\[ \varphi(x) = x - \frac{f(x)}{f'(x)} = x - \frac{(x-\alpha)^m g(x)}{(x-\alpha)^{m-1} g_1(x)} = x - (x- \alpha) \frac{g(x)}{g_1(x)}, \]

pa je njezina derivacija jednaka

\[ \varphi'(x) = 1 - \frac{g(x)}{g_1(x)} - (x-\alpha) \left( \frac{g(x)}{g_1(x)} \right)'. \]

U nultočki \(\alpha\) vrijedi

\[ \varphi'(\alpha) = 1 - \frac{g(\alpha)}{g_1(\alpha)} = 1 - \frac{g(\alpha)}{m g(\alpha)} = 1 - \frac{1}{m}. \]

Za nultočku \(\alpha\) kratnosti \(m \geq 2\), vrijedi \(\varphi'(\alpha) \neq 0\). Po Teoremu 6.16, slijedi da Newtonova metoda tada konvergira samo linearno!

Kad bismo unaprijed znali red nultočke, mogli bismo promatrati modificiranu Newtonovu metodu:

\[ \hat{x}_{n+1} = \hat{x}_n - m \frac{f(\hat{x}_n)}{f'(\hat{x}_n)}. \]

Pokažite da za pripadnu iteracijsku funkciju \(\hat{\varphi}\) tada vrijedi

\[ \hat{\varphi}'(\alpha) = 0, \]

pa modificirana Newtonova metoda ponovno konvergira barem kvadratično. U praksi je vrlo teško unaprijed znati je li nultočka višestruka, a kamoli kolika joj je kratnost.

Alternativno, umjesto rješavanja jednadžbe \(f(x) = 0\), možemo rješavati jednadžbu \(u(x) = 0\), gdje je \(u(x) = \frac{f(x)}{f'(x)}\). Funkcija \(u\) ima iste nultočke kao i \(f\), no sve imaju kratnost \(1\). Zbog toga, Newtonova metoda za funkciju \(u\) koja definira niz

\[ \tilde{x}_{n+1} = \tilde{x}_n - \frac{u(\tilde{x}_n)}{u'(\tilde{x}_n)} \]

konvergira barem kvadratično. Nedostatak ovog pristupa je što, da bismo izračunali \(u'(\tilde{x}_n)\) treba izračunati \(f''(\tilde{x}_n)\), odnosno, sada se pojavila i druga derivacija od \(f\).

Primjeri

Na dva primjera usporedit ćemo brzinu konvergencije metode bisekcije i Newtonove metode. Samo radi ilustracije ovih metoda, napravit ćemo sljedeće modifikacije ranije napravljenih implementacija:

• Metode će vraćati sve izračunate iteracije, a ne samo zadnju. Metoda bisekcije će vraćati i polja svih \(a_n\), \(b_n\).

• Metodama ćemo poslati i „egzaktno” izračunato rješenje \(\alpha\) izračunato metodom bisekcije s toleracijom \(10^{-15}\). Takvo rješenje u praksi naravno ne možemo/želimo izračunati - upravo tome i služe metode poput Newtonove.

• Iteracije ćemo zaustaviti nakon n_max iteracija ili kada bude \(|\alpha - x_n| \leq \eps\). Ponovno, u praksi moramo koristiti neki od kriterija zaustavljanja koje smo gore izveli.

Show code cell source Hide code cell source

import numpy as np;

def bisekcija_v2( f, a, b, eps, n_max, alpha ):
    fa = f(a); fb = f(b);

    x = np.array( [] );
    aovi = np.array( [] );
    bovi = np.array( [] );
    
    # Ponavljamo sve dok je širina segmenta [a, b] veća od eps.
    for n in range( 0, n_max ):
        # Odredimo polovište trenutnog segmenta.
        xn = (a + b) / 2;

        # Dodamo ga u polje svih izračunatih iteracija.
        x = np.append( x, xn );
        aovi = np.append( aovi, a );
        bovi = np.append( bovi, b );

        # Zaustavljamo iteracije ako je |alpha - x_n| < eps.
        if( abs( alpha - xn ) < eps ):
            break;

        fx = f(xn);
        if( fx == 0 ):
            # Možda smo pogodili direktno u nultočku. Vrlo malo vjerojatno.
            break;
        elif( fa*fx < 0 ):
            # Unutar [a, x] je nultočka -> to postaje novi [a, b].
            b = xn; fb = fx;
        else: 
            # Vrijedi fx*fb < 0.
            # Unutar [x, b] je nultočka -> to postaje novi [a, b].
            a = xn; fa = fx;

    return (x, aovi, bovi);


def crtaj_tablicu_bisekcija( f, x, alpha ):
    n = x.shape[0];

    print( ' n      a_n            b_n          x_n          f(x_n)       |alpha-x_n|' );
    print( '-------------------------------------------------------------------------' );
    for k in range( 0, n ):
        print( f'{k:2d}  {a[k]:.10f}  {b[k]:.10f}  {x[k]:.10f}  {f(x[k]):>13.10f}  {abs(alpha-x[k]):.10f}' );

Show code cell source Hide code cell source

def newton_v2( f, df, x0, eps, n_max, alpha ):
    # U polje svih iteracija stavimo samo x0.
    x = np.array( [x0] );
    
    xn = x0;
    for n in range( 1, n_max ):
        # Iduća aproksimacija.
        xn = xn - f(xn) / df(xn);

        # Dodamo ga u polje svih izračunatih iteracija.
        x = np.append( x, xn );

        # Zaustavljamo iteracije ako je |alpha - x_n| < eps.
        if( abs( alpha - xn ) < eps ):
            break;

    return x;


def crtaj_tablicu_newton( f, x, alpha, exp=False ):
    n = x.shape[0];

    print( ' n        x_n                f(x_n)          |alpha-x_n|' );
    print( '-----------------------------------------------------------' );
    for k in range( 0, n ):
        if( exp ):
            print( f'{k:2d}  {x[k]:>17.10e}  {f(x[k]):>18.10e}  {abs(alpha-x[k]):.12e}' );
        else:
            print( f'{k:2d}  {x[k]:>17.14f}  {f(x[k]):>18.14f}  {abs(alpha-x[k]):.14f}' );

Primjer 1. Izračunajmo \(\sqrt[3]{1.5}\), odnosno, nađimo realnu, pozitivnu nultočku \(\alpha\) funkcije

\[ f(x) = x^3 - 1.5. \]

Jednostavno je detektirati da vrijedi \(\alpha \in [1, 2]\). Kako je

\[ f(1) = -0.5 < 0, \quad f(2) = 6.5 > 0, \]

zbog neprekidnosti od \(f\) postoji nultočka unutar \([1, 2]\). No kako \(f\) strogo raste na \(\langle 0, \infty \rangle\), ta nultočka je ujedno i jedina pozitivna nultočka od \(f\).

Metodom bisekcije s točnosti \(\eps = 10^{-15}\) možemo prvo odrediti „egzaktnu” vrijednost nultočke: \(\alpha \approx 1.1447142425533317\).

# Funkcija čiju nultočku želimo odrediti.
def f( x ):
    return x*x*x - 1.5;

# "Egzaktno" rješenje s apsolutnom greškom 10^(-15).
# Početni interval [a, b] = [1, 2].
alpha = bisekcija( f, 1, 2, 1e-15 );
print( f'alpha = {alpha:.16f}' );

alpha = 1.1447142425533317

Sada ponovno pokrenimo metodu bisekcije, te promotrimo koliko joj iteracija treba da odredi tu nultočku s apsolutnom greškom \(\eps = 10^{-8}\).

# Metoda bisekcije, za eps = 10^(-8).
# Početni interval je [a, b] = [1, 2].
# Ova verzija funkcije vraća sve iteracije.
(x_bisekcija, a, b) = bisekcija_v2( f, 1, 2, 1e-8, 50, alpha );
crtaj_tablicu_bisekcija( f, x_bisekcija, alpha );

 n      a_n            b_n          x_n          f(x_n)       |alpha-x_n|
-------------------------------------------------------------------------
 0  1.0000000000  2.0000000000  1.5000000000   1.8750000000  0.3552857574
 1  1.0000000000  1.5000000000  1.2500000000   0.4531250000  0.1052857574
 2  1.0000000000  1.2500000000  1.1250000000  -0.0761718750  0.0197142426
 3  1.1250000000  1.2500000000  1.1875000000   0.1745605469  0.0427857574
 4  1.1250000000  1.1875000000  1.1562500000   0.0458068848  0.0115357574
 5  1.1250000000  1.1562500000  1.1406250000  -0.0160179138  0.0040892426
 6  1.1406250000  1.1562500000  1.1484375000   0.0146842003  0.0037232574
 7  1.1406250000  1.1484375000  1.1445312500  -0.0007192492  0.0001829926
 8  1.1445312500  1.1484375000  1.1464843750   0.0069693550  0.0017701324
 9  1.1445312500  1.1464843750  1.1455078125   0.0031217756  0.0007935699
10  1.1445312500  1.1455078125  1.1450195312   0.0012004442  0.0003052887
11  1.1445312500  1.1450195312  1.1447753906   0.0002403928  0.0000611481
12  1.1445312500  1.1447753906  1.1446533203  -0.0002394794  0.0000609222
13  1.1446533203  1.1447753906  1.1447143555   0.0000004439  0.0000001129
14  1.1446533203  1.1447143555  1.1446838379  -0.0001195210  0.0000304047
15  1.1446838379  1.1447143555  1.1446990967  -0.0000595393  0.0000151459
16  1.1446990967  1.1447143555  1.1447067261  -0.0000295479  0.0000075165
17  1.1447067261  1.1447143555  1.1447105408  -0.0000145521  0.0000037018
18  1.1447105408  1.1447143555  1.1447124481  -0.0000070541  0.0000017944
19  1.1447124481  1.1447143555  1.1447134018  -0.0000033051  0.0000008408
20  1.1447134018  1.1447143555  1.1447138786  -0.0000014306  0.0000003639
21  1.1447138786  1.1447143555  1.1447141171  -0.0000004934  0.0000001255
22  1.1447141171  1.1447143555  1.1447142363  -0.0000000247  0.0000000063

Vidimo da metodi bisekcije:

• Treba čak \(22\) iteracije da bi došla do aproksimacije \(x_{22} = 1.1447142363\) čija je apsolutna greška manja od \(10^{-8}\).

• Promotrimo specijalno stupac \(f(x_n)\) i stupac \(|\alpha - x_n|\).

• Vidimo da se broj vodećih nula u tim stupcima povećava za \(1\) otprilike svake \(3\) iteracije.

• To odgovara linearnoj konvergenciji metode bisekcije.

Promotrimo sada što se dogodi kada pokrenemo Newtonovu metodu. Kako je funkcija \(f'(x) = 3x^2\) konstantnog predznaka na \([1, 2]\), kao i funkcija \(f''(x) = 6x\), metoda će konvergirati za bilo koju početnu točku \(x_0\) takvu da je \(f(x_0) f''(x_0) > 0\). Stoga možemo uzeti desni rub segmenta, \(x_0 = 2\).

# Newtonova metoda treba i derivaciju funkcije f.
def df( x ):
     return 3*x*x;

x_newton = newton_v2( f, df, 2, 1e-12, 50, alpha );
crtaj_tablicu_newton( f, x_newton, alpha );

 n        x_n                f(x_n)          |alpha-x_n|
-----------------------------------------------------------
 0   2.00000000000000    6.50000000000000  0.85528575744667
 1   1.45833333333333    1.60149016203704  0.31361909078000
 2   1.20732426303855    0.25983433061998  0.06261002048522
 3   1.14790497826656    0.01257813452771  0.00319073571323
 4   1.14472310335774    0.00003483308497  0.00000886080441
 5   1.14471424262192    0.00000000026962  0.00000000006859
 6   1.14471424255333    0.00000000000000  0.00000000000000

Vidimo da Newtonovoj metodi:

• Treba samo \(6\) iteracija da bi došla do aproksimacije \(x_{5} = 1.14471424255333\) čija je apsolutna greška manja od \(10^{-12}\).

• Promotrimo specijalno stupac \(f(x_n)\) i stupac \(|\alpha - x_n|\).

• Vidimo da se broj vodećih nula u tim stupcima podupla u svakoj iteraciji.

• To odgovara kvadratnoj konvergenciji Newtonove metode.

Nacrtajmo i graf apsolutnih grešaka za Newtonovu i metodu bisekcije.

Show code cell source Hide code cell source

import matplotlib.pyplot as plt;

plt.semilogy( abs( alpha - x_bisekcija ), label='bisekcija' );
plt.semilogy( abs( alpha - x_newton ), label='Newton' );

plt.xlabel( 'iteracija $n$' );
plt.ylabel( '$|\\alpha - x_n|$' );
plt.title( 'Apsolutne greške u Newtonovoj i metodi bisekcije' );
plt.legend();

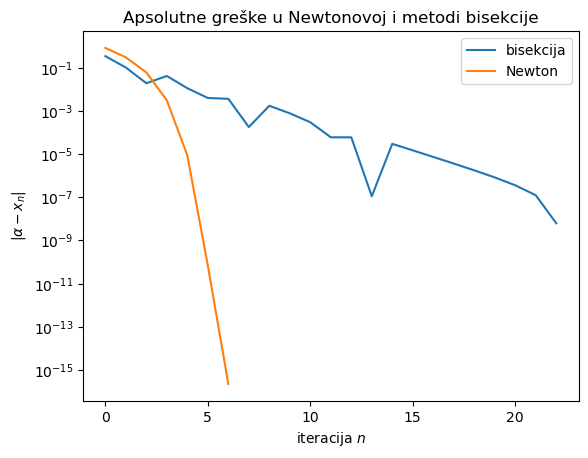
Graf apsolutnih grešaka za bisekciju je gotovo pravac, što ponovno odgovara linearnom redu konvergencije; povremeni skok se može dogoditi kada je polovište segmenta u nekoj iteraciji „slučajno” blizu nultočke, iako je širina segmenta i dalje prevelika da bismo zaustavili iteracije. Iz ovog grafa je teško detektirati red konvergencije Newtonove metode, no on je očito veći od \(1\).

Red konvergencije \(p\) možemo empirijski odrediti nakon izračunatog niza iteracija: treba vrijediti

\[ \lim_n \frac{|\alpha - x_n|}{|\alpha - x_{n-1}|^p} = c > 0, \]

za neku konstantu \(c\). Dakle, za dovoljno velike \(k\) očekujemo

\[ |\alpha - x_k| \approx c {|\alpha - x_{k-1}|^p}. \]

Promotrimo ovu relaciju za \(k=n-1\) i \(k=n-2\). Kako \(x_n \to \alpha\), očekujemo da će \(x_{n}\) biti dovoljno bolja aproksimacija za \(\alpha\) od \(x_{n-1}\) i \(x_{n-2}\) da te relacije možemo zamijeniti sa

\[\begin{split} \begin{align*} |x_{n} - x_{n-1}| &\approx c {|x_{n} - x_{n-2}|^p}, \\ |x_{n} - x_{n-2}| &\approx c {|x_{n} - x_{n-3}|^p}. \end{align*} \end{split}\]

Kada podijelimo ove dvije približne jednakosti, eliminiramo \(c\) i dobivamo

\[\begin{split} \frac{|x_{n} - x_{n-1}|}{|x_{n} - x_{n-2}|} \approx \frac{|x_{n} - x_{n-2}|^p}{|x_{n} - x_{n-3}|^p}, \\ \end{split}\]

iz čega možemo procijeniti red konvergencije

\[ p \approx \frac{\log( |x_{n} - x_{n-1}| / |x_{n} - x_{n-2}| )}{\log( |x_{n} - x_{n-2}| / |x_{n} - x_{n-3}| )}. \]

Napravimo to za Newtonovu metodu i \(n=3, 4, 5, 6\).

Show code cell source Hide code cell source

def tablica_red_konvergencije( x ):
    n_size = x.shape[0];

    print( ' n      p  ' );
    print( '-------------' );
    for n in range( 3, n_size ):
        brojnik  = np.log( abs( x[n] - x[n-1] ) / abs( x[n] - x[n-2] ) );
        nazivnik = np.log( abs( x[n] - x[n-2] ) / abs( x[n] - x[n-3] ) );
        p = brojnik / nazivnik;

        print( f'{n:2d}  {p:.7f}' );

tablica_red_konvergencije( x_newton );

 n      p  
-------------
 3  1.6373782
 4  1.8489351
 5  1.9775015
 6  1.9993717

Zaista, čini se da vrijednost od \(p\) teži prema \(2\), što je red konvergencije Newtonove metode.

Primjer 2. U ovom primjeru ćemo vidjeti kako ponašanje Newtonove metode ovisi o izboru početne točke \(x_0\).

Promotrimo funkciju

\[ f(x) = \arctg(x). \]

Njezina jedina nultočka je \(\alpha = 0\). Međutim, vidjet ćemo da postoji točka \(\beta\) takva da vrijedi:

• Ako \(|x_0| < |\beta|\), onda Newtonova metoda s početnom točkom \(x_0\) konvergira.

• Ako \(|x_0| > |\beta|\), onda Newtonova metoda s početnom točkom \(x_0\) divergira.

• Ako \(|x_0| = |\beta|\), onda Newtonova metoda s početnom točkom \(x_0\) ima periodičko ponašanje.

Odredimo prvo \(x_0\) tako da vrijedi \(x_{1} = -x_0\). Zbog neparnosti funkcije \(f\) tada će vrijediti

\[ x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} = -x_0 - \frac{-f(x_0)}{-f'(x_0)} = -x_1 = x_0, \]

pa slijedi \(x_0 = x_2 = x_4 = \ldots\) i \(x_1 = x_3 = x_5 = \ldots\) i ponašanje Newtonove metode je periodičko. Iz \(x_1 = -x_0\) imamo jednadžbu

\[ x_0 - \frac{f(x_0)}{f'(x_0)} = -x_0 \; \implies \; \arctg(x_0) = \frac{2x_0}{1 + x_0^2}. \]

Rješenje ove nelinearne jednadžbe možemo odrediti npr. metodom bisekcije. Rješenje \(x_0\) će biti upravo ta granična vrijednost \(\beta\).

Show code cell source Hide code cell source

def g(x):
    return np.arctan(x) - 2*x / (1 + x*x);

beta = bisekcija( g, 1, 2, 1e-15 );
print( f'beta = {beta:.16f}' );

beta = 1.3917452002707345

Na slici vidimo geometrijsku reprezentaciju predviđenog periodičkog ponašanja za \(x_0 = \beta\): tangenta na graf funkcije \(f\) u točki \((\beta, f(\beta))\) siječe x-os točno u točki \((-\beta, 0)\), a tangenta u točki \((-\beta, f(-\beta))\) siječe x-os u \((\beta, 0)\).

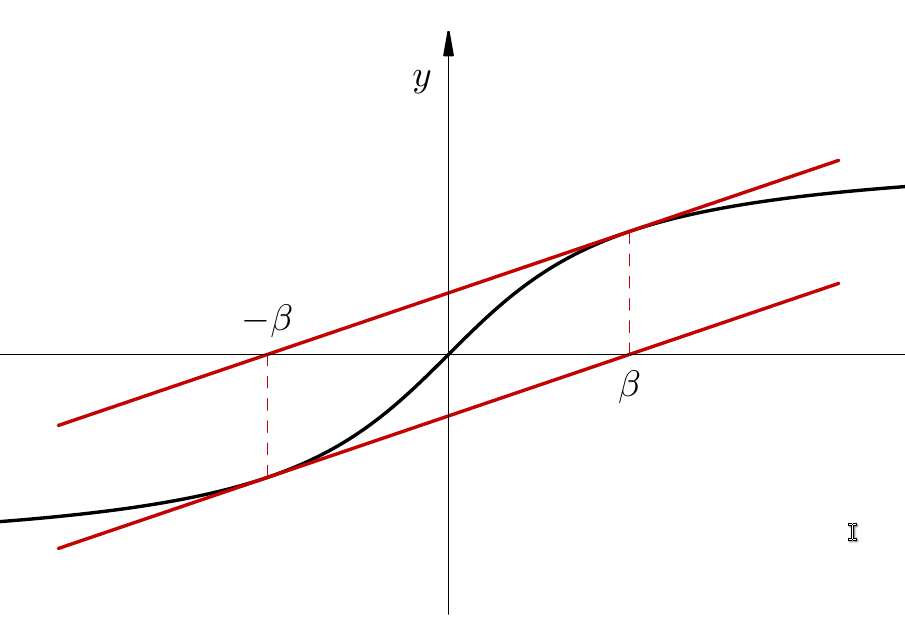
Ispišimo \(10\) Newtonovih iteracija s početnom točkom \(x_0 = \beta\):

Show code cell source Hide code cell source

def f(x):
    return np.arctan(x);

def df(x):
    return 1 / (1 + x*x);

x0 = beta;
x_newton = newton_v2( f, df, x0, 1e-12, 10, 0 );
crtaj_tablicu_newton( f, x_newton, 0 );

 n        x_n                f(x_n)          |alpha-x_n|
-----------------------------------------------------------
 0   1.39174520027073    0.94774713351699  1.39174520027073
 1  -1.39174520027073   -0.94774713351699  1.39174520027073
 2   1.39174520027073    0.94774713351699  1.39174520027073
 3  -1.39174520027073   -0.94774713351699  1.39174520027073
 4   1.39174520027071    0.94774713351698  1.39174520027071
 5  -1.39174520027067   -0.94774713351697  1.39174520027067
 6   1.39174520027056    0.94774713351693  1.39174520027056
 7  -1.39174520027029   -0.94774713351684  1.39174520027029
 8   1.39174520026955    0.94774713351659  1.39174520026955
 9  -1.39174520026761   -0.94774713351593  1.39174520026761

Zaista, iteracije su (skoro) periodičke, do minimalnog odstupanja dolazi zbog grešaka zaokruživanja.

Promotrimo što se dogodi za neki \(|x_0| > \beta\), na primjer, uzmimo \(x_0 = 1.5\). Metoda očito divergira. Interpretirajte to geometrijski na gornjoj slici.

Show code cell source Hide code cell source

x0 = 1.5;
x_newton = newton_v2( f, df, x0, 1e-12, 10, 0 );
crtaj_tablicu_newton( f, x_newton, 0, exp=True );

 n        x_n                f(x_n)          |alpha-x_n|
-----------------------------------------------------------
 0   1.5000000000e+00    9.8279372325e-01  1.500000000000e+00
 1  -1.6940796006e+00   -1.0375463591e+00  1.694079600554e+00
 2   2.3211269614e+00    1.1640020424e+00  2.321126961438e+00
 3  -5.1140878368e+00   -1.3776945287e+00  5.114087836778e+00
 4   3.2295683914e+01    1.5398423269e+00  3.229568391421e+01
 5  -1.5753169508e+03   -1.5701615340e+00  1.575316950821e+03
 6   3.8949760078e+06    1.5707960701e+00  3.894976007761e+06
 7  -2.3830288974e+13   -1.5707963268e+00  2.383028897355e+13
 8   8.9202801611e+26    1.5707963268e+00  8.920280161124e+26
 9  -1.2499045994e+54   -1.5707963268e+00  1.249904599366e+54

Konačno, uzmimo neki \(|x_0| < \beta\), na primjer, \(x_0 = 1\).

Show code cell source Hide code cell source

x0 = 1.0;
x_newton = newton_v2( f, df, x0, 1e-12, 10, 0 );
crtaj_tablicu_newton( f, x_newton, 0 );

 n        x_n                f(x_n)          |alpha-x_n|
-----------------------------------------------------------
 0   1.00000000000000    0.78539816339745  1.00000000000000
 1  -0.57079632679490   -0.51866936925502  0.57079632679490
 2   0.11685990399891    0.11633226511390  0.11685990399891
 3  -0.00106102211704   -0.00106102171889  0.00106102211704
 4   0.00000000079631    0.00000000079631  0.00000000079631
 5   0.00000000000000    0.00000000000000  0.00000000000000

Metoda sada konvergira prema nultočki \(\alpha = 0\) i to u svega \(5\) koraka; interpretirajte to geometrijski na gornjoj slici. Procijenimo i njezin red konvergencije.

Show code cell source Hide code cell source

tablica_red_konvergencije( x_newton );

 n      p  
-------------
 3  2.7945973
 4  2.9644227
 5  2.9994217

Numerički red konvergencije je ispao \(3\). To se podudara s teorijom jer za \(f(x) = \arctg(x)\) vrijedi \(f''(0) = 0\).