Show code cell source Hide code cell source

import numpy as np;
from scipy.linalg import svd;
from PIL import Image;
import matplotlib.pyplot as plt;
import requests;

	
%matplotlib inline

4.5. Primjene

Osim u problemima najmanjih kvadrata, alati i pojmovi koje smo spomenuli i prošlim lekcijama koriste se i u nekim neuobičajenim primjerima. Pokazat ćemo ih nekoliko.

Komprimiranje slika

Teorem 4.11 pokazuje nam da se da za neku matricu kojoj nam nije bitan njezin original nego neka aproksimacija možemo uštedjeti mnogo memorije ukoliko pamtimo skraćeni zapis SVD-a njezine aproksimacije nižeg ranga. Pokažimo to na primjeru komprimiranja slika.

Slike su u računalu u pravilu reprezentirane trima matricama (svaka čuva informacije o jednoj od RGB boja) kojima dimenzije ovise o razlučivosti (pikseli). Radi jednostavnosti, fokusirajmo se na one crno-bijele (tj. one u nijansama sive). Neka je ta slika/matrica \(A\) dimenzije \(M \times N\), i neka je \(r \ll M,N\) rang aproksimacijske matrice. Umjesto čuvanja \(M\times N\) podataka originalne slike, u računalu možemo spremiti samo prvih \(r\) stupaca matrica \(U\) i \(V\) iz singularne dekompozicije matrice \(A\) zajedno s njihovih \(r\) najvećih singularnih vrijednosti, što znači da bismo pamtili \(r\cdot (M+N+1)\) podataka. Za jako male \(r\) ušteda je velika, ali je velika i razlika između originalne slike i aproksimativne. Ipak, moguće je izabrati neke \(r\) za koje štedimo, a greška aproksimacije nije loša.

Uzmimo crno-bijelu verziju slike s naslovnice weba PMF-MO , i pogledajmo kako izgledaju aproksimacije te slike matricama različitih rangova.

Show code cell source Hide code cell source

# Učitavanje slike, pretvorba u crno bijelu, i spremanje u matricu A.
img_url = 'https://www.pmf.unizg.hr/_pub/carousel/8f883877aae0193238e6c9aa6ccb439d1633939087.jpg';
img = Image.open( requests.get(img_url, stream = True).raw ).convert('L');
A = np.asarray(img);

memory_A = A.shape[0] * A.shape[1];
print( f'Dimenzije slike / matrice A: {A.shape[0]} x {A.shape[1]}' );
print( f'Originalna slika zauzima: {memory_A} doubleova' );

# SVD originalne slike/matrice.
(U, S, Vt) = svd(A);

# Graf singularnih vrijednosti.
plt.figure();
plt.semilogy( S );
plt.title( 'Singularne vrijednosti matrice A' );
plt.xlabel( 'k' );
plt.ylabel( '$\sigma_k$' );

# Rangovi na koje komprimiramo sliku / matricu A.
ranks = [10, 50, 200, 715];

print( 'Komprimirane slike: ' );
for i in range(len(ranks)):
    r = ranks[i];

    # Skraceni SVD
    S_r = np.diag(S[:r]);
    U_r = U[:, :r];
    Vt_r = Vt[:r,:];

    # Aproksimacija slike
    X = U_r @ S_r @ Vt_r;

    # Vrijednosti van intervala [0, 255] treba vratiti u interval.
    X[X < 0] = 0;
    X[X > 255] = 255;

    # Memorijsko zauzeće.
    memory_X = (U_r.shape[0] + 1 + Vt_r.shape[1]) * r;
    compression = memory_X / memory_A;

    # Konverzija iz matrice u sliku.
    compressed_img = Image.fromarray( X.astype(np.uint8) );

    # Relativna greška aproksimacije = sigma_{r+1} / sigma_1.
    if( r < S.shape[0] ):
        rel_err = S[r] / S[0];
    else:
        rel_err = 0;

    print(f"  Rang: {r:3d}; slika zauzima: {memory_X:8d} doubleova ({100*compression:6.2f}% originalne); rel. greška: {rel_err:.4f}.")

    plt.figure();
    plt.imshow( compressed_img, cmap='gray');
    plt.title( f'rank={r}' );

plt.figure();
plt.imshow( img, cmap='gray');
plt.title( f'Original' );

Dimenzije slike / matrice A: 715 x 1920
Originalna slika zauzima: 1372800 doubleova
Komprimirane slike: 
  Rang:  10; slika zauzima:    26360 doubleova (  1.92% originalne); rel. greška: 0.0714.
  Rang:  50; slika zauzima:   131800 doubleova (  9.60% originalne); rel. greška: 0.0304.
  Rang: 200; slika zauzima:   527200 doubleova ( 38.40% originalne); rel. greška: 0.0134.
  Rang: 715; slika zauzima:  1884740 doubleova (137.29% originalne); rel. greška: 0.0000.

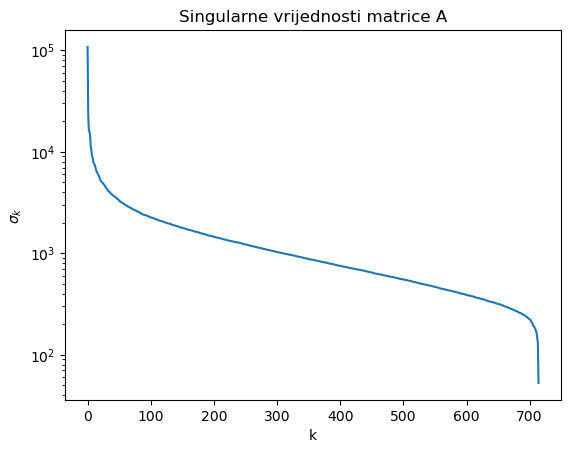
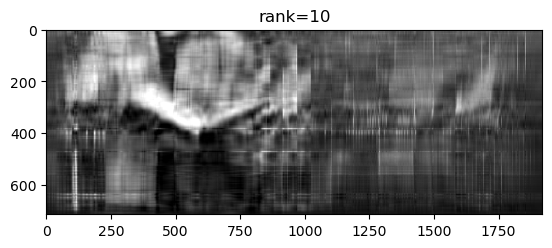
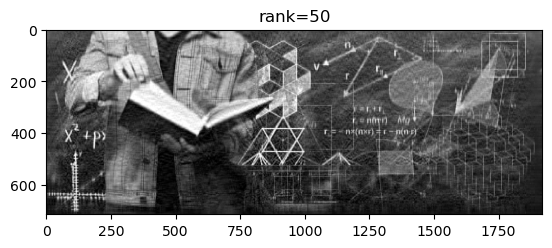
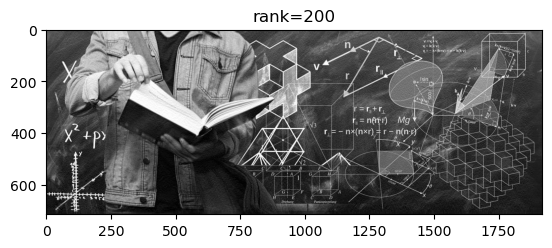
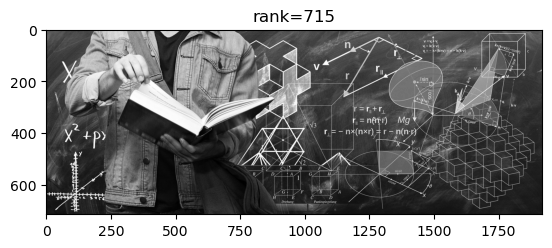
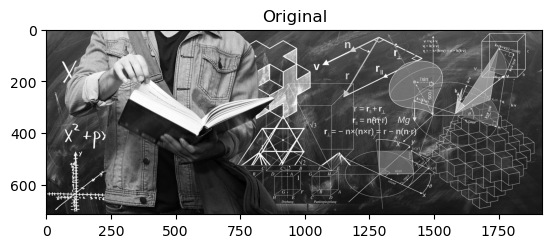
Vidimo da singularne vrijednosti matrice \(A\) u početku vrlo brzo padaju. Ako uzmemo aproksimaciju \(X\) ranga \(r=50\), onda relativna greška iznosi \(\frac{\|A - X\|_2}{\|A\|_2} = \frac{\sigma_{51}}{\sigma_1} \approx 0.0304\), pa se komprimirana slika razlikuje od originalne u samo \(\approx 3\%\).

Prepoznavanje rukom pisanih znamenki

Pokažimo primjenu naučenih alata za prepoznavanje rukom pisanih znamenki. Pretpostavimo da nam je dan klasificiran skup rukom pisanih znamenaka (tzv. training set), tj. skup slika znamenaka za koje je netko označio o kojoj se znamenci radi i koja služi učenju našeg algoritma. Cilj je za svaku novu sliku znamenke (iz tzv. test seta) odrediti o kojoj se znamenci radi. Kao i prije, slike su reprezentirane matricama piksela, te kao i prije, pretpostavimo samo da se radi o crno-bijelim slikama.

Fiksirajmo neku znamenku i promotrimo sve slike/matrice iz training seta koje odgovaraju toj znamenci. Kako bismo ih mogli lakše proučiti, sve slike/matrice pretvorimo u vektor stupac (slažući stupce te slike jedan na drugi), te ih spojimo u jednu veliku matricu. Recimo, ako se za neku znamenku (recimo \(4\)) u training setu nalazi \(1000\) slika/matrica dimenzija \(28\times 28\) piksela na kojima znamo da je napisana znamenka \(4\), svaku od slika/matrica pretvorit ćemo prvo u jedan vektor duljine \(28\cdot 28 = 784\). Zatim ćemo sve te vektore posložiti jedan do drugog kao stupce u jednu matricu dimenzije \(784 \times 1000\). Time smo dobili matricu koju ćemo za potrebe nastavka zvati \(M^{(4)}\).

Ključna pretpostavka na kojoj se temelji ovaj algoritam, koja možda nije intuitivna, ali se ispostavlja da vrijedi, je da je svaki vektor duljine \(784\) koji predstavlja neku sliku znamenke \(4\) blizak linearnoj kombinaciji nekoliko vektora tipičnih za tu znamenku \(4\). Dakle, postoje vektori \(u_1^{(4)},u_2^{(4)},\dots,u_r^{(4)} \in \R^{784}\) takvi da za svaki vektor \(w\) koji predstavlja sliku znamenke \(4\) vrijedi

\[w \approx \lambda_1 u_1^{(4)} + \lambda_2 u_2^{(4)} + \dots + \lambda_r u_r^{(4)},\]

za neke skalare \(\lambda_1,\lambda_2,\dots,\lambda_r\) (koji ovise o \(w\)).

Te vektore \(u_1^{(4)},u_2^{(4)},\dots,u_r^{(4)}\) možemo odrediti iz SVD-a matrice \(M^{(4)}\). Naime, svaki stupac te matrice element je slike matrice \(M^{(4)}\), a ona je razapeta lijevim singularnim vektorima, dakle stupcima matrice \(U^{(4)}\) iz SVD-a matrice \(M^{(4)} = U^{(4)} \Sigma^{(4)} V^{(4),T}\). Ako želimo uzeti samo neke singularne vektore, uzet ćemo one koji odgovaraju najvećim singularnim vrijednostima. Dakle, za \(u_1^{(4)},u_2^{(4)},\dots,u_r^{(4)}\) uzimamo prvih \(r\) stupaca matrice \(U^{(4)}\). Da su ti vektori najbolji za ovu priliku možemo opravdati Teoremom 4.11. Način odabira broja \(r\) je nejasan: što je manji, manje informacija uzimamo iz training seta, a što je veći, previše se podudaramo s training setom. Ovo ponavljamo za sve znamenke.

Za svaku novu sliku, tj. svaki vektor \(w\) koji predstavlja sliku znamenke koju treba klasificirati trebamo naći onu znamenku \(z \in \{0,1,\ldots,9\}\) za koju je greška u aproksimaciji

\[w \approx \lambda_1 u_1^{(z)} + \lambda_2 u_2^{(z)} + \dots + \lambda_r u_r^{(z)}\]

najmanja (skalari \(\lambda_i\) ovise o \(w\) i \(z\)). Ako za svaku znamenku promatramo grešku u toj jednakosti

\[\text{err}_z := \min_{\lambda \in \R^{r}} \left\|w - \sum_{i=1}^r \lambda_i u_i^{(z)} \right\|_2\]

prepoznajemo diskretan problem najmanjih kvadrata za svaku znamenku \(z\) s vektorom \(w\) i matricom \(U^{(z)}(:,1:r)\). Algoritam onda može reći da je se na slici reprezentiranom vektorom \(w\) nalazi ona znamenka \(z\) za koju je greška \(\text{err}_z\) najmanja.

Dakle, algoritam glasi:

• Za svaku znamenku \(z\in \{0,1,\dots,9\}\) stvorimo matricu \(M^{(z)}\) stvorenu od vektoriziranih stupaca slika iz training seta na kojima se nalazi znamenka \(z\).

• Izračunamo SVD matrice \(M^{(z)}\) i zapamtimo prvih \(r\) stupaca matrice \(U^{z}\) (to zovemo \(U^{(z)}(:,1:r)\)).

• Za svaki novu znamenku iz test seta reprezentiranu vektorom \(w\) riješimo \(10\) problema najmanjih kvadrata s matricom \(U^{(z)}(:,1:r)\), te proglasimo da je \(w\) ona znamenka za koju je greška u problemu najmanjih kvadrata najmanja.

• Uočimo da je greška u problemu najmanjih kvadrata jednaka normi ortogonalne projekcije vektora \(w\) na potprostor generiran s \(Q=U^{(z)}(:,1:r)\), tj. \(\text{err}_z = \|w - Q Q^T w\|_2\).

Primijetimo da kako rješavamo probleme najmanjih kvadrata s ortogonalnim matricama, pa ne trebamo provoditi QR faktorizaciju te matrice, budući da znamo kako ta QR faktorizacija glasi.

U nastavku pogledajmo implementaciju ovog algoritma.

Show code cell source Hide code cell source

# Ovo je pripremna faza algoritma gdje učitavamo znamenke iz kolekcije MNIST.
# Ovdje još ne radimo SVD, već samo učitavamo podatke.
import numpy as np;
import matplotlib.pyplot as plt;

# Podaci se nalaze u sklopu biblioteke tensorflow.
from tensorflow.keras.datasets import mnist;
from tensorflow.keras.utils import to_categorical;

# Učitamo cijelu kolekciju za treniranje i testiranje.
(x_train, y_train), (x_test, y_test) = mnist.load_data();

# Izdvojimo prvih 4096 podataka za treniranje i 16 za testiranje.
x_train = x_train[:4096]; y_train = y_train[:4096];
x_test  = x_test[:16];    y_test  = y_test[:16];

# Skaliramo slike tako da su u njima brojevi između 0 i 1.
x_train = x_train / 255.0; x_test = x_test / 255.0;

# x_train[i] je PxP matrica (P=28). Konvertiramo ih u vektore duljine n=P^2.
P = x_train[0].shape[0]; 
n = P*P;

# Razmotamo matrice u vektore (dimenzije n=28*28=784).
x_train = x_train.reshape(-1, n);
x_test  = x_test.reshape(-1, n);

# Još treba transponirati matricu (u kolekciji je svaki primjer jedan redak).
x_train = x_train.T;
x_test  = x_test.T;

# Sada imamo matrice: 
# x_train dimenzije 784x4096 - svaki stupac je jedna slika neke znamenke, to koristimo za učenje.
# y_train dimenzije 4096 - svaki element je znamenka kojoj pripada slika u x_train.
# x_test dimenzije 784x16 - svaki stupac je jedna slika neke znamenke, to koristimo za testiranje.
# y_test dimenzije 16 - svaki element je znamenka kojoj pripada slika u x_test.

# U dict U_svi ćemo spremiti prvih 7 lijevih singularnih vektora za svaku znamenku k.
U_svi = {};
for k in range(10):
    # Za svaku znamenku k napravimo matricu Mk u kojoj su sve njene slike.
    # Nađi sve indexe u x_train na kojima se nalazi znamenka k.
    index_k = (y_train == k);
    Mk = x_train[:, index_k];

    # Mk je dimenzije 784xNk, gdje je Nk broj slika znamenke k.
    # Zapamti samo prvih 7 lijevih singularnih vektora za kasniju klasifikaciju.
    [Uk, sk, Vk] = np.linalg.svd(Mk, full_matrices=True);
    U_svi[k] = Uk[:, :7];

# Završili smo pripremnu fazu i sada radimo testiranje klasifikatora.
# Grafički prikaz.
fig = plt.figure(figsize=[16, 16]);

for i in range( 0, 16 ):
    # Sada ćemo pomoću SVD-a pokušati odrediti koja je to znamenka.
    # Nađi onu znamenku koja ima najmanju grešku u problemu najmanjih kvadrata s matricom Uk.
    greske = np.zeros( 10 );
    for k in range(10):
        Uk = U_svi[k];
        # Greška = norma projekcije slike x_test[:,i] na potprostor generiran stupcima od Uk.
        greske[k] = np.linalg.norm( x_test[:,i] - Uk.dot( Uk.transpose().dot(x_test[:,i]) ) );
    znamenka_SVD = np.argmin(greske);

    # Znamenka koja se zapravo nalazi na slici x_test[:,i].
    znamenka_zapravo = y_test[i];

    # Nacrtaj sliku znamenke i ispiši predviđanje pomoću SVD i koja je to znamenka zapravo.
    ax1 = fig.add_subplot(4, 4, i+1);
    ax1.title.set_text( f'SVD: {znamenka_SVD}, zapravo: {znamenka_zapravo}' );
    ax1.imshow( x_test[:, i].reshape(28, 28), cmap='gray' );

plt.show();

Vidimo da algoritam koji koristi SVD za klasifikaciju znamenki radi jako dobro i da je ispravno klasificirao sve znamenke iz testnog skupa osim jedne znamenke 5 (koju je klasificirao kao 6, no sliku je teško prepoznati i ljudskim okom). Uočite da za klasifikacije novih znamenki nije potrebno ponovno računati SVD matrica \(M^{(z)}\) za svaku znamenku, već je dovoljno samo koristiti matrice \(U^{(z)}\) koje smo jednom izračunali i spremili u U_svi.

Ovaj algoritam dugo se koristio u određivanju rukom pisanih poštanskih brojeva i razvrstavanju u poštanskim uredima u SAD-u. Više o ovom i sličnim algoritmima možete pročitati u [Elden07].

Literatura

[Elden07]

Lars Eldén. Matrix methods in data mining and pattern recognition. Volume 4 of Fundamentals of Algorithms. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2007. ISBN 978-0-898716-26-9. URL: https://doi.org/10.1137/1.9780898718867, doi:10.1137/1.9780898718867.