Show code cell source
import numpy as np;
import scipy as sc;
import matplotlib.pyplot as plt;
from scipy.special import eval_legendre
from scipy.integrate import quad
%matplotlib inline
4.4. Neprekidni problem najmanjih kvadrata#
Sjetimo se ponovno problema najmanjih kvadrata u punoj općenitosti: za zadanu funkciju \(f: X \to \R\) cilj je naći što bolju aproksimacijsku funkciju \(\varphi\) među svim funkcijama \(\psi\) iz određenog skupa \(\mathcal S\):
Neprekidni problem najmanjih kvadrata je gore opisan problem u kojem skup \(X\) više nije diskretan skup nego interval \([a,b]\) (ili neki (polu)otvoreni interval). Skup \(\mathcal S\) je sada skup funkcija na tom skupu. Kao i prije, promatrat ćemo samo vektorske prostore funkcija, konkretno konačnodimenzionalne potprostore prostora svih neprekidnih funkcija \(\mathcal C ([a,b];\R)\). Jedan primjer takvog potprostora je \(\mathcal P_m\), prostor polinoma stupnja manjeg ili jednakog \(m\).
Prirodna norma na \(\mathcal C ([a,b];\R)\) je takozvana \(L^2\)–norma: za neprekidnu funkciju \(g : [a,b] \to \mathbb R\) definiramo
Ako integral smatramo „beskonačnom sumom”, onda je ova norma „beskonačni” analogon euklidske norme \(\| g\| = \displaystyle \left( \sum_{i=1}^n g(t_i)^2 \right)^{1/2}\) na diskretnom skupu \(\{t_1,\dots,t_n\}\). Uz normu \(\| \cdot \|_{L^2([a,b];\R)}\) prirodno se definira njoj kompatibilan skalarni produkt
Lako je provjeriti da ova norma i skalarni produkt zadovoljavaju uvjete iz definicije norme i skalarnog produkta. U ovoj cjelini će biti posebno važno da ta norma i skalarni produkt zadovoljavaju sve ono što i inače vrijedi na konačnodimenzionalnim prostorima te smo učili na kolegijima Linearna algebra 1 i 2, a navikli koristiti na prostoru \(\mathbb R^m\) (npr. ortogonalnost i Gram-Schmidtov postupak). Nadalje, u ovoj cjelini s „\(L^2\)” označavamo normu i skalarni produkt na neprekidnim funkcijama, a s „\(2\)” označavamo normu i skalarni produkt na vektorima u \(\mathbb R^m\).
Ako je \(\{ \varphi_1, \dots, \varphi_m\}\) baza vektorskog prostora \(\mathcal S\) u kojem tražimo rješenje, cilj je naći funkciju
takvu da je norma razlike
što manja. Koristeći svojstva skalarnog produkta, provodimo raspis sličan onom u Primjeru 4.4. Imamo
gdje je
\(M \in \R^{m \times m}\) matrica takva da joj na mjestu \((i,j)\) piše \(\left\langle \varphi_i , \varphi_j \right\rangle_{L^2}\),
\(p \in \R^{m}\), \(p_i = \left\langle \varphi_i , f \right\rangle_{L^2}\),
\(\alpha \in \R\), \(\alpha = \left\langle f , f \right\rangle_{L^2([a,b];\R)}\).
Dobiveni izraz možemo promatrati kao funkciju u varijablama \(x_1,\dots,x_m \in \R\). To je glatka i konveksna (dapače, kvadratna) funkcija koja postiže globalni minimum u stacionarnoj točki, pa je zato \(x\) rješenje sustava
Ovaj sustav naziva se sustavom normalnih jednadžbi. Izveden je na analogan način kao u Primjeru 4.4. Možemo dokazati da ovaj sustav ima jedinstveno rješenje ako je \(\{ \varphi_1, \dots, \varphi_m\}\) baza vektorskog prostora \(\mathcal S\).
Sustav (4.2) ima jedinstveno rješenje \(x\).
Dovoljno je pokazati da je matrica \(M \in \R^{m \times m}\), definirana tako da na mjestu \((i,j)\) piše \(\left\langle \varphi_i , \varphi_j \right\rangle_{L^2}\), regularna.
Prvo dokažimo da je pozitivno definitna: za svaki \(x\in \mathbb R^m\), \(x\not=0\), vrijedi
gdje je \(\psi := \displaystyle \sum_{i=1}^m x_i \varphi_i \in \mathcal S\). Kako je \(\|\cdot\|^2_{L^2}\) norma na \(\mathcal S\), ona je nenegativna, pa smo upravo dokazali da je \(M\) pozitivno semidefinitna. Nadalje, po definiciji norme, \(\|\psi \|_{L^2}\) može biti jednako nula samo ako je \(\psi = 0\), a kako je \(\{ \varphi_1, \dots, \varphi_m\}\) baza za \(\mathcal S\), to je moguće samo ako su svi skalari \(x_i\) jednaki nula, čime dobivamo kontradikciju. Dakle, \(M\) je pozitivno definitna matrica, što znači da su joj sve svojstvene vrijednosti pozitivne (prema Propoziciji 2.12), nijedna joj nije jednaka nuli, pa je regularna.
U diskretnom problemu najmanjih kvadrata zaključili smo da rješavanje sustava normalnih jednadžbi nije nužno numerički optimalan način rješavanja. Možemo pomisliti da će slično biti i u neprekidnom slučaju.
Neprekidnim problemom najmanjih kvadrata nađimo najbolju aproksimaciju funkcije \(f(x)=\ch x\) na \([0,1]\) na prostoru polinoma stupnja manjeg ili jednakog \(20\).
Da bismo riješili ovaj problem, uzimamo standardnu bazu polinoma \(\{1,x,x^2, \dots, x^{20} \}\), te moramo naći matricu \(M\in \R^{21\times 21}\) i vektor \(p\in \R^{21}\).
Matrica \(M\) ne ovisi o funkciji \(f\). Na mjestu \((i,j)\) imamo
Dakle, matrica \(M\) zapravo je Hilbertova matrica \(H_{21}\), matrica za koju smo vidjeli da je katastrofalno uvjetovana. Propozicija 4.12 posebno dokazuje da je ona pozitivno definitna.
Iako postaje jasno da ovo nije put kako rješavati ovaj problem, napomenimo kako se mogu u ovom slučaju odrediti vrijednosti vektora \(p\):
Te integrale tražimo parcijalnom integracijom, rekurzivno po \(i\). Za \(i=0\) i \(i=1\) imamo
Za veće \(i\) imamo
Dakle, ponovno vidimo da problem najmanjim kvadratima ne treba rješavati sustavom normalnih jednadžbi. Inspirirani boljim pristupom kod diskretnog problema, slutimo da ćemo i ovaj problem stabilnije riješiti ako elemente baze ortogonaliziramo.
Legendreovi polinomi#
Pretpostavimo da je \(\{P_0, P_1, P_2, \ldots, P_m \}\) ortogonalna baza s obzirom na skalarni produkt \(\langle \cdot, \cdot \rangle_{L^2}\) (ne nužno i ortonormirana, dakle ne zahtijevamo da su norme polinoma jednake \(1\)) dobivena iz baze \(\{1,x,x^2,\dots,x^m\}\) za \(\mathcal P_m\). Tada je matrica sustava normalnih jednadžbi dijagonalna! Naime, za svaka dva različita indeksa \(i\) i \(j\) vrijedi da je na mjestu \((i,j)\) zapisana vrijednost \(\left\langle P_i , P_j \right\rangle_{L^2} = 0\). Kako je lako riješiti dijagonalne sustave, znamo eksplicitno rješenje najmanjih kvadrata: to je \(\varphi \in \mathcal P_m\) takva da je
Dakle, jedino nam je preostalo odrediti ortogonalnu bazu za \(\{1,x,x^2,\dots,x^m\}\), što možemo Gram-Schmidtovim postupkom (bez normiranja). Iz izgleda Hilbertove matrice je jasno da kanonska baza nije ortogonalna. Može se postaviti pitanje je li se netko već sjetio gledati polinome koji čini ortogonalnu bazu i znaju li se neka svojstva takvih polinoma?
Niz polinoma \((P_n)_{n\geq 0}\) zadan tročlanom rekurzijom
naziva se niz Legendreovih polinoma.
Dajemo glavno svojstvo Legendreovih polinoma zbog kojih ih uvodimo, bez dokaza.
Niz Legendreovih polinoma je ortogonalan na \([-1,1]\). Preciznije: za svaka dva različita nenegativna cijela broja \(k\) i \(\ell\) vrijedi
Dodatno, za svaki nenegativan cijeli broj \(k\) vrijedi
Gornji teorem pokazuje ortogonalnost Legendreovih polinoma na \([-1,1]\). U slučaju generalne domene \([a,b]\) potrebno je reskalirati te polinome afinim preslikavanjem, kao što smo vidjeli kod Čebiševljevih polinoma. Također, Legendreovi polinomi zadovoljavaju tročlanu rekurziju kao i Čebiševljevi polinomi prve vrste, te se iz nje vidi da je \(P_n\) polinom stupnja \(n\). Dakle, za svaki \(k\in \mathbb N_0\) skup \(\{P_0,P_1,\dots,P_k\}\) ortogonalan je skup od \(k+1\) polinoma u \(\mathcal P_k\), pa je nužno baza za \(\mathcal P_k\), dakle razapinje isti prostor kao \(\{1,x,\dots,x^k \}\). Dodavanjem novog polinoma \(P_{k+1}\) u taj skup proširujemo taj skup polinomom stupnja \(k+1\) koji je ortogonalan na preostale elemente baze. Isto se događa i Gram-Schmidtovim postupkom, iz kojeg na jedinstven način dobivamo ortonormiranu bazu iz kanonske. Zaključujemo da je Legendreova baza \(\{P_0, P_1, \ldots, P_m\}\), do na skalar(e), upravo ona baza dobivena ortonormiranjem kanonske baze \(\{1, x, \ldots, x^m\}\) za \(\mathcal P_m\).
Promotrimo ponovno Primjer 4.13, pri čemu sada promatramo interval \([a, b]=[-1, 1]\) umjesto \([0, 1]\). Umjesto u standardnoj bazi, rješenje \(\varphi\) možemo pronaći u Legendreovoj bazi koristeći (4.3):
Dodatna prednost korištenja Legendreove baze vidi se i kada želimo proširiti skup \(\mathcal{S}\) tako da obuhvaća i polinome stupnja \(m+1\). Za račun preko normalnih jednadžbi bi trebalo nanovo formirati i rješavati sustav s punom matricom \(H_{m+1}\). Za rješavanje problema preko Legendreovih polinomima trebamo odrediti samo jedan novi koeficijent \(x_{m+1}\) u sumi \(\sum_{i=0}^{m+1} x_i P_i\), dok su koeficijenti \(x_0, \ldots, x_m\) isti kao kod aproksimacije iz \(\mathcal{P}_m\).
Usporedimo te račune u Pythonu.
Show code cell source
def hilbert(m):
# Formiranje Hilbertove matrice "M" za sustav "M*x=p".
M = np.zeros((m+1, m+1))
for i in range(m+1):
for j in range(m+1):
M[i, j] = 1 / (i + j + 1)
return M
def hilbert_rhs(m):
# Formiranje desne strane "p" za sustav "M*x=p" s Hilbertovom matricom.
p = np.zeros(m+1)
for i in range(m+1):
def f(x):
return x**i * np.cosh(x)
# Uoči: ovdje integriramo od 0 do 1.
integral = quad(f, 0, 1)
p[i] = integral[0]
return p
def legendre_solution(m):
# Formula za rješenje pomoću Legendreovih polinoma.
# Vraćamo vektor koeficijenata u linearnoj kombinaciji P_0, ..., P_m.
y = np.zeros(m+1)
for i in range(m+1):
def f(x):
# eval_legendre vraća vrijednost i-tog Leg. polinoma u točki x
return eval_legendre(i, x) * np.cosh(x)
# Uoči: ovdje integriramo od -1 do 1 jer su na tom intervalu Leg. polinomi ortogonalni.
# Aproksimacija će biti dobra na cijelom tom intervalu. Crtat ćemo samo na [0, 1].
integral = quad(f, -1, 1)
y[i] = integral[0] * (2*i+1) / 2.
return y
# Tražimo aproksimaciju iz skupa polinoma P_20.
m = 20
# Traženje polinoma Hilbertovom matricom, za interval [a, b] = [0, 1].
M = hilbert(m)
p = hilbert_rhs(m)
coeffs_std = np.linalg.solve(M, p)
# Računanje koeficijenata u bazi Legendreovih polinoma, za interval [a, b] = [-1, 1].
coeffs_legendre = legendre_solution(m)
def phi_std(x, coeffs):
# Računanje phi(x) = coeffs[0] + coeffs[1]*x + ... + coeffs[n-1]*x^{n-1}.
n = len(coeffs)
result = 0
for i in range(n-1, -1, -1):
# Hornerov algoritam!
result = result * x + coeffs[i]
return result
def phi_legendre(x, coeffs):
# Računanje phi(x) = coeffs[0]*P_0(x) + coeffs[1]*P_1(x) + ... + coeffs[n-1]*P_{n-1}(x).
n = len(coeffs)
result = 0
for i in range(n):
# eval_legendre je iz biblioteke scipy.special.
# Ovo je neefikasno! Bolje: generalizirani Hornerov algoritam.
result = result + eval_legendre(i, x) * coeffs[i]
return result
# Grafički prikaz rezultata na intervalu [0, 1].
# Uoči: Legendre radi dobru aproksimaciju na cijelom [-1, 1].
x = np.linspace(0, 1, 500)
y = np.cosh(x)
plt.subplot( 1, 2, 1 )
plt.plot(x, phi_std(x, coeffs_std), label='Aproksimacija polinomom Hilbert')
plt.plot(x, phi_legendre(x, coeffs_legendre), label='Aproksimacija polinomom Legendre')
plt.plot(x, y, label='f(x) = ch(x)')
plt.legend()
plt.show()
plt.subplot( 1, 2, 2 )
plt.semilogy(x, abs(phi_std(x, coeffs_std)-y), label='Greska Hilbert')
plt.semilogy(x, abs(phi_legendre(x, coeffs_legendre)-y), label='Greska Legendre')
plt.legend()
plt.show()
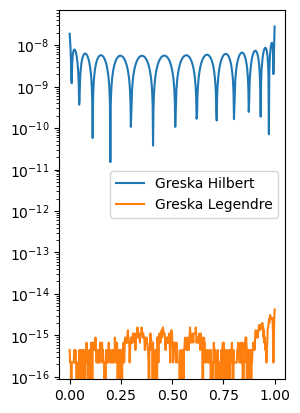
Skalare u kanonskoj bazi i Legendreovoj bazi, iako možemo izračunati eksplicitno, zbog čistoće koda računamo numerički. Također, evaluacija Legendreovih polinoma u gornjem kodu zbog čitkosti koda vrši se na loš način, inače se i za njih može implementirati Hornerova shema kao ona za kanonsku bazu. Unatoč tome, kao što vidimo na grafovima, greška rješavanja Hilbertovom matricom ne vidi se toliko na lijevom grafu (sva tri grafa se poklapaju) koliko na desnom: apsolutne greške su reda \(10^{-8}\), dok su za polinom pronađen Legendreovim polinomom reda \(10^{-15}\).
Napomena
Legendreovi polinomi već su druga familija rekurzivno zadana familija polinoma koju spominjemo na ovom kolegiju, nakon Čebiševljevih polinoma prve vrste. To su samo neke familije tzv. ortogonalnih polinoma (i Čebiševljevi polinomi prve vrste su ortogonalni u odnosu na skalarni produkt \(\langle f,g\rangle := \int_{-1}^1 \frac{f(x)g(x)}{\sqrt{1-x^2}} dx\), za koje se razvila posebna generalna teorija te za koju su rezultati iz ove cjeline posebni slučajevi.
Linearnu kombinaciju ortogonalnih polinoma poput \(\varphi(t) = \sum_{i=0}^m x_i P_i(t)\) možemo efikasno evaluirati u nekoj točki \(t \in \R\) korištenjem generaliziranog Hornerovog algoritma. Taj algoritam iskorištava rekurzivnu formulu kojom je definiran niz ortogonalnih polinoma \(P_0, P_1, \ldots, P_m\).
Trigonometrijske funkcije#
Navedimo još jedan primjer neprekidnog problema najmanjih kvadrata.
Trigonometrijske funkcije
čine ortogonalnu familiju funkcija na \([-\pi,\pi]\). Preciznije, za različite nenegativne cijele brojeve \(k\) i \(\ell\) vrijedi
te za sve prirodne brojeve \(k\) vrijedi
Zadnja tvrdnja očito vrijedi. Koristeći formule pretvorbe iz umnoška u zbroj i da za sve cijele \(a\) različite od nula vrijedi
za sve nenegativne cijele \(k\) i \(\ell\) imamo
Sada imamo:
ako su \(k\) i \(\ell\) različiti nenegativni cijeli brojevi, tada su oba broja \(k+\ell\) i \(k-\ell\) različiti od nule, pa je integral svake od šest podintegralnih trigonometrijskih funkcija na desnoj strani jednak nuli;
ako je \(k=\ell \in \N\), integrali četiri od šest podintegralnih funkcija na desnoj strani jednaki su nula: kako je \(\sin 0x = 0\), iz druge relacije zajedno s prošlim slučajem dokazali smo ortogonalnost svih funkcija, a kako je \(\cos 0x = 1\), dobivamo
slučaj \(k=\ell=0\) je promatran na početku dokaza.
Koristeći rezultat ove propozicije i (4.3), dobivamo da je funkcija
gdje je
rješenje neprekidnog problema najmanjih kvadrata za funkciju \(f:[-\pi,\pi]\to \mathbb R\) na skupu
U slučaju kada možemo pustiti \(N\to \infty\), red
nazivamo Fourierovim redom za funkciju \(f\). Koeficijenti \(a_k\) i \(b_k\) zovu se Fourierovi koeficijenti. Teorija Fourierovih redova izlazi iz materije teorije numeričke matematike, a ima razne primjere, poput rješavanja diferencijalnih jednadžbi, obradi zvukova i signala i sl.
Radi potpunosti, bez dokaza navodimo jedan rezultat konvergencije.
Neka je funkcija \(f : [-\pi,\pi] \to \mathbb R\) takva da su \(f\) i \(f'\) po dijelovima neprekidne funkcije. Tada za svaki \(x\in [-\pi,\pi] \) Fourierov red \(S_f(x)\) funkcije \(f\) konvergira, te vrijedi
Posebno, u unutarnjim točkama domene u kojima \(f\) nema prekid Fourierov red ima vrijednost funkcije \(f\).