3.4. Po dijelovima polinomna interpolacija

Ideja po dijelovima polinomne interpolacije

Ako je zadana funkcija \(f : [a, b] \to \R\), interpolacija polinomom koju smo radili do sada pokušava odrediti jedan polinom koji aproksimira funkciju \(f\) na cijelom intervalu. Zbog toga se može dogoditi da taj polinom treba biti visokog stupnja.

Umjesto toga, za zadane čvorove \(a = x_0 < x_1 < \ldots < x_n = b\), po dijelovima polinomna interpolacija na svakom intervalu \([x_{k-1}, x_k]\) koristi novi polinom \(p_k\) niskog stupnja (mi ćemo promatrati stupnjeve 1 i 3) koji interpolira \(f\) samo na tom podintervalu.

Funkciju \(f\), dakle, aproksimiramo funkcijom \(\varphi\), gdje je \( \varphi(x) = \left\{ \begin{array}{c} p_1(x), \quad x \in [x_0, x_1], \\ p_2(x), \quad x \in [x_1, x_2], \\ \vdots \\ p_n(x), \quad x \in [x_{n-1}, x_n]. \end{array}\right. \) Uvjeti interpolacije ostaju isti: \(\varphi(x_k) = f(x_k)\) u svim čvorovima. Iz ovih uvjeta odmah slijedi da je funkcija \(\varphi\) neprekidna.

Povećanjem broja čvorova/podintervala \(n\) ćemo smanjivati grešku interpolacije, a stupnjevi polinoma \(p_k\) i dalje ostaju isti.

Za zadanu vrijednost \(x \in [a, b]\) vrijednost \(\varphi(x)\) izračunavamo tako da prvo pronađemo \(k \in \{1, \ldots, n\}\) takav da je \(x \in [x_{k-1}, x_k]\) i onda izračunamo \(\varphi(x) = p_k(x)\). Takav \(k\) možemo efikasno odrediti pomoću binarnog pretraživanja:

def get_k( cvor, x ):
    # Funkcija vraća index k takav da je cvor[k-1] <= x < cvor[k].
    lo = 0; hi = len(cvor);
    while( hi - lo > 1 ):
        mid = (lo + hi) // 2;
        if( x < cvor[mid] ):
            hi = mid;
        else:
            lo = mid;
    return lo+1;

Ovaj algoritam ima složenost \(\bigO(\log n)\).

Ako je mreža ekvidistantna, onda naravno nije potrebno binarno pretraživanje.

Po dijelovima linearna interpolacija

Pretpostavimo prvo su polinomi \(p_k\) stupnja 1, za sve \(k=1, \ldots, n\). Takvu interpolaciju zovemo po dijelovima linearna interpolacija.

Polinom \(p_k\) zapišimo u obliku

\[ p_k(x) = c_{0, k} + c_{1, k} (x - x_{k-1}), \quad x \in [x_{k-1}, x_k]. \]

Ovaj oblik koristimo umjesto \(p_k(x) = b + ax\) kako veličina koeficijenata ne bi ovisila o podintervalu na kojem radimo interpolaciju nego samo o vrijednostima funkcije \(f\) na tom podintervalu.

Polinom \(p_k\) određujemo iz uvjeta interpolacije na rubovima podintervala: \(p_k(x_{k-1}) = f(x_{k-1}) = f_{k-1}\), \(p_k(x_k) = f(x_k) = f_k\). Postoji jedinstveni takav polinom stupnja 1. Zapišimo ga u Newtonovoj formi:

\[ p_k(x) = f[x_{k-1}] + f[x_{k-1}, x_k] (x - x_{k-1}). \]

Sada odmah dobivamo koeficijente:

\[\begin{split} \begin{align*} c_{0, k} &= f[x_{k-1}] = f_{k-1}, \\ c_{1, k} &= f[x_{k-1}, x_k] = \frac{f_k - f_{k-1}}{x_k - x_{k-1}}. \end{align*} \end{split}\]

Greška ovakve interpolacije u točki \(x\) se podudara s greškom interpolacije s odgovarajućim linearnim polinomom \(p_k\). Prirodno pitanje koje se postavlja: ako povećavamo broj podintervala, koliko brzo će se smanjivati greška? Odgovor daje sljedeći teorem.

Teorem 3.25 (Greška po dijelovima linearne interpolacije)

Neka je \(f \in C^2[(a, b)]\), te neka je \(\varphi\) po dijelovima linearna interpolacija funkcije \(f\) u čvorovima \(a = x_0 < x_1 < \ldots < x_n = b\).

Ako je \(h = \max_{k=1, \ldots, n} |x_k - x_{k-1}|\) maksimalna širina podintervala te \(M_2 = \max_{x \in [a, b]} |f''(x)|\), onda za sve \(x \in [a, b]\) vrijedi

\[ |f(x) - \varphi(x)| \leq \frac{1}{8} h^2 M_2. \]

Dokaz.

Prema Teoremu 3.10, za \(x \in [x_{k-1}, x_k]\) vrijedi

(3.13)\[ |f(x) - \varphi(x)| = |f(x) - p_k(x)| \leq |\omega_k(x)| \frac{M_2^{(k)}}{2!},\]

gdje je \(\omega_k(x) = (x - x_{k-1})(x - x_k)\) polinom čvorova za linearnu interpolaciju u čvorovima \(x_{k-1}\) i \(x_k\), a

\[ M_2^{(k)} = \max_{x \in [x_{k-1}, x_k]} |f''(x)|. \]

Pronađimo gornju ogradu za \(|\omega_k(x)|\). Funkcija \(\omega_k(x)\) je kvadratna; u rubovima intervala \([x_{k-1}, x_k]\) poprima vrijednost nula, a u unutrašnjosti poprima samo negativne vrijednosti. Pri tome joj je minimum upravo u polovištu \(x_e = \frac{x_{k-1} + x_k}{2}\). Stoga za sve \(x \in [x_{k-1}, x_k]\) vrijedi

\[ |\omega_k(x)| \leq |\omega_k(x_e)| = |(x_e - x_{k-1})(x_e - x_k)| = \frac{(x_k - x_{k-1})^2}{4} \leq \frac{h^2}{4}. \]

Vratimo se s ovom ocjenom u (3.13):

\[ |f(x) - \varphi(x)| \leq |\omega_k(x)| \frac{M_2^{(k)}}{2!} \leq \frac{h^2}{4} \frac{M_2}{2!} = \frac{1}{8} h^2 M_2, \]

što je i trebalo dokazati.

Iz gornjeg teorema slijedi da ako ravnomjerno povećavamo broj čvorova \(n\), tako da maksimalni razmak \(h \to 0\) kada \(n \to \infty\), onda i maksimalna greška po dijelovima linearne interpolacije teži u \(0\), tj. imamo uniformnu konvergenciju!

Na primjer, za ekvidistantnu mrežu

\[ x_k = a + k \cdot h, \quad h = \frac{b-a}{n}, \]

greška je reda veličine \(h^2\):

\[ \|f - \varphi\|_{\infty} \leq \frac{1}{8} h^2 M_2 = \frac{(b-a)^2 M_2}{8 n^2}, \]

Vidimo da greška pada s kvadratom broja čvorova: ako udvostručimo broj čvorova, ocjena greške će postati 4 puta manja.

Unatoč uniformnoj konvergenciji, po dijelovima linearna interpolacija ima sljedeće mane:

• Tipično je potreban velik broj podintervala \(n\) da se dobije umjerena točnost aproksimacije.

• Dobivena funkcija \(\varphi\) nije dovoljno glatka – samo je neprekidna.

Ove nedostatke ćemo riješiti tako da na svakom intervalu uzmemo polinom samo malo većeg stupnja: već će polinomi stupnja 3 biti dovoljni.

Iako po dijelovima linearnu interpolaciju vrlo lagano možemo implementirati sami (probajte!), još je jednostavnije u Pythonu koristiti ugrađenu funkciju interp iz biblioteke numpy.

import numpy as np;

# Definiramo polje čvorova interpolacije. 
x = np.array( [-1, -0.5, 0, 0.5, 1] );

# Izračunamo vrijednosti funkcije f u tim čvorovima, npr. za f(x)=cos(x): 
y = np.cos(x);

# Funkcija np.interp( 0.25, x, y ) evaluira PD linearnu interpolaciju definiranu
# čvorovima x i vrijednostima y u točki 0.25.
print( 'f(0.25)   = ', np.cos(0.25) );
print( 'phi(0.25) = ', np.interp( 0.25, x, y ) );

f(0.25)   =  0.9689124217106447
phi(0.25) =  0.9387912809451864

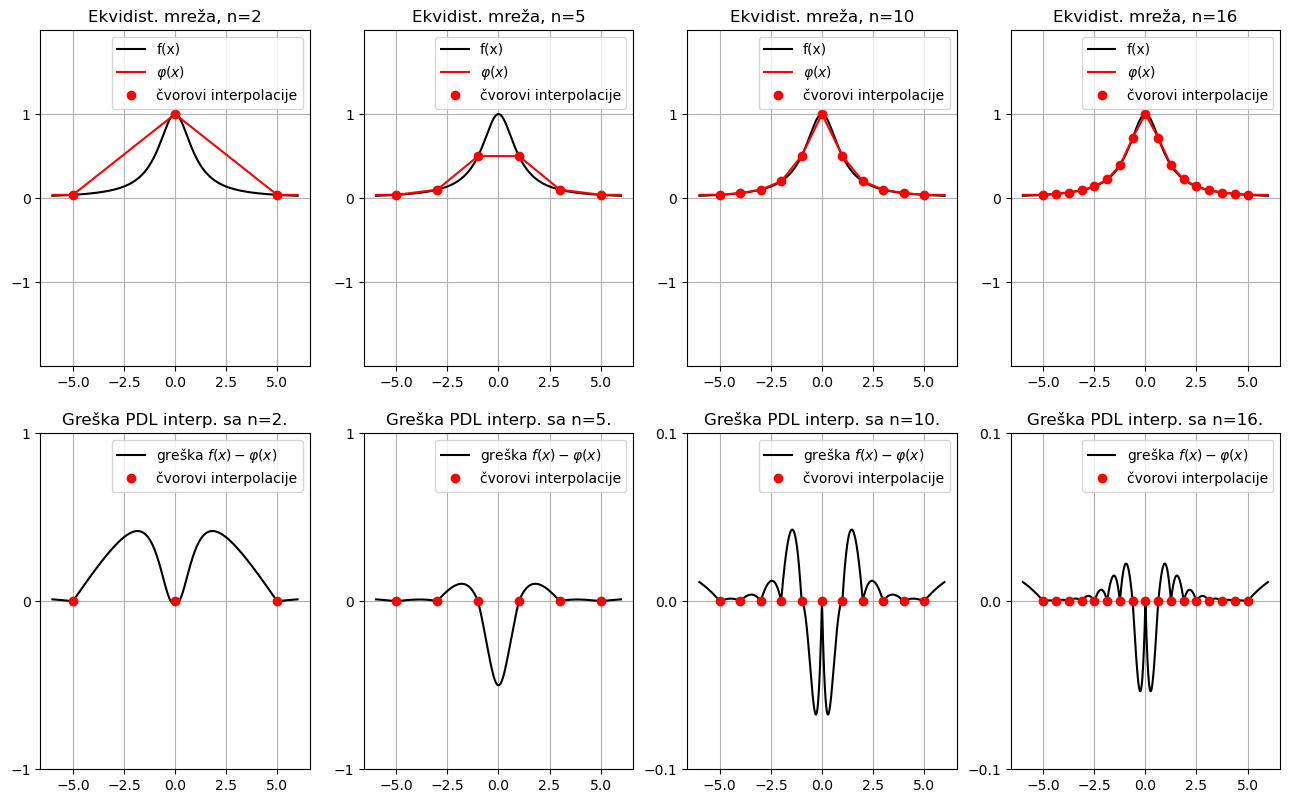
Primjer. Promotrimo ponovno funkciju Runge \(f(x) = \frac{1}{1+x^2}\) na intervalu \([-5, 5]\) i njezinu interpolaciju po dijelovima linearnom interpolacijom. Koristimo ekvidistantnu mrežu redom s \(n=2, 5, 10, 16\) čvorova. Uočite da smanjujemo skalu na y-osi grafova greške!

Usporedite dobiveno sa svim ranijim interpolacijama.

Show code cell source Hide code cell source

import numpy as np;
import matplotlib.pyplot as plt;

def interpoliraj( n, graf ):
    # Čvorovi interpolacije: n+1 ekvidistantna točka između 0.1 i 1, uključujući rubove.
    x = np.linspace(-5, 5, num=n+1);

    # Vrijednosti funkcije f u čvorovima interpolacije.
    f = 1 / (1 + x * x);
    
    # Točke u kojima želimo izračunati vrijednost funkcije phi.
    # Uzet ćemo 1000 točaka u intervalu [-6, 6].
    xx = np.linspace(-6, 6, num=1000);

    # Evaluiramo PD linearnu interpolaciju u svim točkama iz xx odjednom.
    yy = np.interp( xx, x, f );

    # Vrijednosti funkcije Runge u točkama xx.
    ff = 1 / (1 + xx * xx);  

    # Nacrtamo graf interpolacijskog polinoma i funkcije Runge, te čvorove interpolacije.
    plt.subplot( 2, 4, graf );
    plt.plot(xx, ff, 'k-', label='f(x)');
    plt.plot(xx, yy, 'r-', label='$\\varphi(x)$');
    plt.plot(x, f, 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();
    plt.ylim(-2, 2);
    plt.yticks(ticks=[0, -1, 1]);
    plt.title('Ekvidist. mreža, n=' + str(n));

    # Nacrtamo graf za grešku, te čvorove interpolacije.
    plt.subplot( 2, 4, 4+graf );
    plt.plot(xx, yy-ff, 'k-', label='greška $f(x)-\\varphi(x)$');
    plt.plot(x, np.zeros_like(x), 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();

    if( n > 5 ):
        plt.ylim(-0.1, 0.1);
        plt.yticks(ticks=[0, -0.1, 0.1]);
    else:
        plt.ylim(-1, 1);
        plt.yticks(ticks=[0, -1, 1]);

    
    plt.title('Greška PDL interp. sa n=' + str(n) + '.');

plt.figure(figsize=[16, 9.6]);

interpoliraj(2, graf=1);
interpoliraj(5, graf=2);
interpoliraj(10, graf=3);
interpoliraj(16, graf=4);

Po dijelovima kubična interpolacija

Kod po dijelovima kubične intepolacije funkcije \(f\) na \([a, b]\), restrikcija aproksimacijske funkcije \(\varphi\) na svaki podinterval \([x_{k-1}, x_k]\) je kubični polinom:

\[ \varphi \big|_{[x_{k-1}, x_k]} = p_k \in \mathcal{P}_3, \quad k=1, \ldots, n. \]

Polinom \(p_k\) ponovno zapisujemo relativno s obzirom na \(x_{k-1}\):

(3.14)\[ p_k(x) = c_{0, k} + c_{1, k} (x - x_{k-1}) + c_{2, k} (x - x_{k-1})^2 + c_{3, k} (x - x_{k-1})^3.\]

Sada trebamo odrediti po 4 koeficijenta za svaki \(p_k\), tj. ukupno imamo \(4n\) nepoznanica. Uvjeti interpolacije

(3.15)\[ p_k(x_{k-1}) = f_{k-1}, \quad p_k(x_k) = f_k,\]

daju ukupno \(2n\) jednadžbi za te nepoznanice i osiguravaju neprekidnost od \(\varphi\) u svim unutrašnjim čvorovima mreže \(x_1, \ldots, x_{n-1}\).

Obično želimo da \(\varphi\) bude glađa, barem klase \(C^1([a, b])\) pa i njezina derivacija mora biti neprekidna u čvorovima. To ćemo osigurati tako da za neke brojeve \(s_0, \ldots, s_n\) zahtijevamo

(3.16)\[ p_k'(x_{k-1}) = s_{k-1}, \quad p_k'(x_k) = s_k.\]

Vrijednosti od \(s_k\) možemo odabrati na bilo koji način, jer će zbog \(p_k'(x_k) = p_{k+1}'(x_k) = s_k\) funkcija \(\varphi\) imati neprekidnu prvu derivaciju. Prirodno je da su ti brojevi derivacije ili aproksimacije derivacije funkcije \(f\) u čvorovima.

Sada za svaki polinom \(p_k\) uvjeti (3.15) i (3.16) definiraju upravo Hermiteov interpolacijski problem u čvorovima \(x_{k-1}\) i \(x_k\). Rješenje u Newtonovoj bazi je

(3.17)\[\begin{split}\begin{align*} p_k(x) &= f[x_{k-1}] + f[x_{k-1}, x_{k-1}] (x - x_{k-1}) \\ &\quad + f[x_{k-1}, x_{k-1}, x_k] (x - x_{k-1})^2 \\ &\quad + f[x_{k-1}, x_{k-1}, x_k, x_k] (x - x_{k-1})^2(x-x_k), \end{align*}\end{split}\]

gdje je \(f[x_{k-1}] = f_{k-1}\), \(f[x_{k-1}, x_{k-1}] = s_{k-1}\), \(f[x_{k}] = f_{k}\), \(f[x_{k}, x_{k}] = s_{k}\), pa pripadna tablica izgleda ovako:

\[\begin{split}\begin{array}{c|ccccc} t_j & f[t_j] & f[t_j, t_{j+1}] & f[t_j, t_{j+1}, t_{j+2}] & f[t_j, t_{j+1}, t_{j+2}, t_{j+3}] \\ \hline x_{k-1} & f_{k-1} & & & \\ & & s_{k-1} & & \\ x_{k-1} & f_{k-1} & & \frac{f[x_{k-1}, x_k] - s_{k-1}}{h_k} & \\ & & f[x_{k-1}, x_k] & & \frac{s_k + s_{k-1} - 2f[x_{k-1}, x_k]}{h_k^2} \\ x_k & f_k & & \frac{s_k - f[x_{k-1}, x_k]}{h_k} & \\ & & s_k & & \\ x_k & f_k & & & \end{array}\end{split}\]

Ovdje je \(h_k = x_k - x_{k-1}\) razmak čvorova. Sada još samo preostaje konvertirati polinom \(p_k\) zapisan u Newtonovoj bazi (3.17) u oblik (3.14):

\[\begin{split}\begin{align*} p_k(x) &= f[x_{k-1}] + f[x_{k-1}, x_{k-1}] (x - x_{k-1}) \\ &\quad + (f[x_{k-1}, x_{k-1}, x_k] - h_k f[x_{k-1}, x_{k-1}, x_k, x_k]) (x - x_{k-1})^2 \\ &\quad + f[x_{k-1}, x_{k-1}, x_k, x_k] (x - x_{k-1})^3, \end{align*}\end{split}\]

iz čega možemo direktno pročitati koeficijente:

\[\begin{split}\begin{align*} c_{0, k} &= f[x_{k-1}] = f_{k-1}, \\ c_{1, k} &= f[x_{k-1}, x_{k-1}] = s_{k-1}, \\ c_{3, k} &= f[x_{k-1}, x_{k-1}, x_k, x_k] = \frac{s_k + s_{k-1} - 2f[x_{k-1}, x_k]}{h_k^2}, \\ c_{2, k} &= f[x_{k-1}, x_{k-1}, x_k] - h_k f[x_{k-1}, x_{k-1}, x_k, x_k] = \frac{f[x_{k-1}, x_k] - s_{k-1}}{h_k} - h_k c_{3, k}. \\ \end{align*}\end{split}\]

Ako su nam zadani brojevi \(f_0, \ldots, f_n\) i \(s_0, \ldots, s_n\), sada znamo odrediti sve polinome \(p_k\), pa time i funkciju \(\varphi\). Preostaje diskusija o tome kako odabrati vrijednosti \(s_k\). Proučit ćemo dva slučaja: po dijelovima kubičnu Hermiteovu interpolaciju i kubične splajnove.

Po dijelovima kubična Hermiteova interpolacija

Kod po dijelovima kubične Hermiteove interpolacije, pretpostavljamo da su nam poznate i vrijednosti derivacije funkcije \(f\) u čvorovima, te stavljamo prirodni zahtjev

\[ p_k'(x_k) = s_k = f'(x_k). \]

Polinom \(p_k\) na intervalu \([x_{k-1}, x_k]\) je dakle rješenje problema Hermiteove polinomne interpolacije funkcije \(f\) u rubnim čvorovima jer ćemo imati podudaranje

\[\begin{split} \begin{alignat*}{2} & p_k(x_{k-1}) = f(x_{k-1}), \quad && p_k(x_{k}) = f(x_{k}), \\ & p_k'(x_{k-1}) = f'(x_{k-1}), \quad && p_k'(x_{k}) = f'(x_{k}). \end{alignat*} \end{split}\]

Proceduru nalaženja koeficijenata od \(p_k\) smo opisali ranije – sada samo uvrstimo \(s_k = f'(x_k)\).

U odnosu na po dijelovima linearnu interpolaciju, sada imamo dosta bolju ocjenu greške.

Teorem 3.26 (Greška po dijelovima kubične Hermiteove interpolacije)

Neka je \(f \in C^4[(a, b)]\), te neka je \(\varphi\) po dijelovima kubična Hermiteova interpolacija funkcije \(f\) u čvorovima \(a = x_0 < x_1 < \ldots < x_n = b\).

Ako je \(h = \max_{k=1, \ldots, n} |x_k - x_{k-1}|\) maksimalna širina podintervala te \(M_4 = \max_{x \in [a, b]} |f^{(4)}(x)|\), onda za sve \(x \in [a, b]\) vrijedi

\[ |f(x) - \varphi(x)| \leq \frac{1}{384} h^4 M_4. \]

Dokaz.

Prema Teoremu 3.24, za \(x \in [x_{k-1}, x_k]\) vrijedi (uvrstimo \(n=1\)):

(3.18)\[ |f(x) - \varphi(x)| = |f(x) - p_k(x)| \leq |\omega^2_k(x)| \frac{M_4^{(k)}}{4!},\]

gdje je \(\omega^2_k(x) = (x - x_{k-1})^2(x - x_k)^2\) polinom čvorova za Hermiteovu interpolaciju u čvorovima \(x_{k-1}\) i \(x_k\), a

\[ M_4^{(k)} = \max_{x \in [x_{k-1}, x_k]} |f^{(4)}(x)|. \]

Pronađimo gornju ogradu za \(|\omega^2_k(x)|\). Kako je \(\omega^2_k(x) \geq 0\),treba pronaći maksimum od \(\omega^2_k(x)\) na \([x_{k-1}, x_k]\). Lokalne ekstreme dobijemo deriviranjem i pokazuje se da je lokalni maksimum ponovno u polovištu \(x_e = \frac{x_{k-1} + x_k}{2}\).

Stoga za sve \(x \in [x_{k-1}, x_k]\) vrijedi

\[ |\omega^2_k(x)| \leq |\omega^2_k(x_e)| = |(x_e - x_{k-1})^2(x_e - x_k)^2| = \frac{(x_k - x_{k-1})^4}{16} \leq \frac{h^4}{16}. \]

Vratimo se s ovom ocjenom u (3.18):

\[ |f(x) - \varphi(x)| \leq |\omega^2_k(x)| \frac{M_4^{(k)}}{4!} \leq \frac{h^4}{16} \frac{M_4}{4!} = \frac{1}{384} h^4 M_4, \]

što je i trebalo dokazati.

Ponovno imamo uniformnu konvergenciju. Za ekvidistantnu mrežu

\[ x_k = a + k \cdot h, \quad h = \frac{b-a}{n}, \]

je sada greška reda veličine \(h^4\):

\[ \|f - \varphi\|_{\infty} \leq \frac{1}{384} h^4 M_4 = \frac{(b-a)^4 M_4}{384 n^4}, \]

Greška pada s četvrtom potencijom broja čvorova: ako udvostručimo broj čvorova, ocjena greške će postati 16 puta manja!

Usporedimo ovu interpolaciju s po dijelovima linearnom:

• Kod po dijelovima linearne interpolacije: ako je \(h \sim 10^{-2}\), očekujemo grešku reda veličine \(h^2 \sim 10^{-4}\).

• Kod po dijelovima kubične Hermiteove interpolacije: ako je \(h \sim 10^{-2}\), očekujemo grešku reda veličine \(h^4 \sim 10^{-8}\).

Ovo naravno ovisi i o funkciji koju interpoliramo, kao i o širini intervala interpolacije, ali daje dobar osjećaj o tome koliko je manja greška kubične interpolacije. Uz to, aproksimacija \(\varphi\) je sada klase \(C^1([a, b])\).

Greška u aproksimaciji derivacija

Izveli smo uniformnu ocjenu greške za interpolaciju funkcije \(f \in C^4([a, b])\) po dijelovima kubičnom funkcijom \(\varphi\).

No može se pokazati da ta funkcija dobro aproksimira i derivacije od \(f\):

\[\begin{split} \begin{align*} \|f - \varphi\|_{\infty} &\leq \frac{1}{384} h^4 \|f^{(4)}\|_{\infty} \\ \|f' - \varphi'\|_{\infty} &\leq \frac{\sqrt{3}}{216} h^3 \|f^{(4)}\|_{\infty} \\ \|f'' - \varphi''\|_{\infty} &\leq \frac{1}{12} h^2 \|f^{(4)}\|_{\infty} \\ \|f''' - \varphi'''\|_{\infty} &\leq \frac{1}{2} h \|f^{(4)}\|_{\infty} \end{align*} \end{split}\]

Vidimo da je greška sve veća za više derivacije (uvijek promatramo malene \(h \ll 1\)), no i dalje u svim slučajevima imamo uniformnu konvergenciju kada broj čvorova \(n \to \infty\)!

Iako po dijelovima kubičnu Hermiteovu interpolaciju vrlo lagano možemo implementirati sami (probajte!), još je jednostavnije u Pythonu koristiti ugrađenu klasu CubicHermiteSpline iz biblioteke scipy.interpolate.

import numpy as np;
import scipy.interpolate as scin;

# Definiramo polje čvorova interpolacije. 
x = np.array( [-1, -0.5, 0, 0.5, 1] );

# Izračunamo vrijednosti funkcije f u tim čvorovima, npr. za f(x)=cos(x):
y = np.cos(x);

# Izračunamo vrijednosti od f' u tim čvorovima, npr:
dy = -np.sin(x);

# Sada možemo konstruirati po dijelovima kubičnu Hermiteovu interpolaciju phi:
phi = scin.CubicHermiteSpline( x, y, dy );

# Objekt phi se sada ponaša kao obična funkcija.
print( 'f(0.25)   = ', np.cos(0.25) );
print( 'phi(0.25) = ', phi(0.25) );

f(0.25)   =  0.9689124217106447
phi(0.25) =  0.9687553771079491

Primjer. Promotrimo ponovno funkciju Runge \(f(x) = \frac{1}{1+x^2}\) na intervalu \([-5, 5]\) i njezinu interpolaciju po dijelovima kubičnom Hermiteovom interpolacijom. Koristimo ekvidistantnu mrežu redom s \(n=2, 5, 10, 16\) čvorova. Uočite da smanjujemo skalu na y-osi grafova greške!

Usporedite dobiveno sa svim ranijim interpolacijama.

Show code cell source Hide code cell source

import numpy as np;
import scipy.interpolate as scin;
import matplotlib.pyplot as plt;

def interpoliraj( n, graf ):
    # Čvorovi interpolacije: n+1 ekvidistantna točka između 0.1 i 1, uključujući rubove.
    x = np.linspace(-5, 5, num=n+1);

    # Vrijednosti funkcije f u čvorovima interpolacije.
    f = 1 / (1 + x * x);
    
    # Vrijednosti derivacije funkcije f u čvorovima interpolacije.
    df = -2*x / ((1 + x*x)**2);

    # PD kubična Hermiteova interpolacija phi pomoću biblioteke scipy.
    phi = scin.CubicHermiteSpline(x, f, df);

    # Točke u kojima želimo izračunati vrijednost funkcije phi.
    # Uzet ćemo 1000 točaka u intervalu [-6, 6].
    xx = np.linspace(-6, 6, num=1000);

    # Evaluiramo phi u točkama xx.
    yy = phi(xx);

    # Vrijednosti funkcije Runge u točkama xx.
    ff = 1 / (1 + xx * xx);  

    # Nacrtamo graf interpolacijske fje phi i funkcije Runge, te čvorove interpolacije.
    plt.subplot( 2, 4, graf );
    plt.plot(xx, ff, 'k-', label='f(x)');
    plt.plot(xx, yy, 'r-', label='$\\varphi(x)$');
    plt.plot(x, f, 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();
    plt.ylim(-2, 2);
    plt.yticks(ticks=[0, -1, 1]);
    plt.title('Ekvidist. mreža, n=' + str(n));

    # Nacrtamo graf za grešku, te čvorove interpolacije.
    plt.subplot( 2, 4, 4+graf );
    plt.plot(xx, yy-ff, 'k-', label='greška $f(x)-\\varphi(x)$');
    plt.plot(x, np.zeros_like(x), 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();

    if( n > 10 ):
        plt.ylim(-0.01, 0.01);
        plt.yticks(ticks=[0, -0.01, 0.01]);
    elif( n > 5 ):
        plt.ylim(-0.1, 0.1);
        plt.yticks(ticks=[0, -0.1, 0.1]);
    else:
        plt.ylim(-1, 1);
        plt.yticks(ticks=[0, -1, 1]);

    
    plt.title('Greška PDKH interp. sa n=' + str(n) + '.');

plt.figure(figsize=[16, 9.6]);

interpoliraj(2, graf=1);
interpoliraj(5, graf=2);
interpoliraj(10, graf=3);
interpoliraj(16, graf=4);

Kubični splajnovi

Vidjeli smo ranije da postavljanje uvjeta

\[\begin{split} \begin{alignat*}{2} &p_k(x_{k-1}) = f(x_{k-1}), \quad && p_k(x_{k}) = f(x_k), \\ &p_k'(x_{k-1}) = s_{k-1}, \quad && p_k'(x_{k}) = s_k \end{alignat*} \end{split}\]

osigurava da je aproksimacijska funkcija \(\varphi\) klase \(C^1([a, b])\). Kod kubične splajn intepolacije, brojeve \(s_k\) nećemo odabrati tako da aproksimiraju \(f'(x_k)\), nego tako da \(\varphi\) bude klase \(C^2([a, b])\).

Dakle, sada moramo osigurati neprekidnost druge derivacije od \(\varphi\) u unutrašnjim čvorovima interpolacije:

\[ p_k''(x_k) = p_{k+1}''(x_k), \quad k=1, 2, \ldots, n-1. \]

Ovaj uvjet će voditi na jednadžbe koje moraju zadovoljavati brojevi \(s_k\). Napišimo ponovno opći oblik polinoma \(p_k\):

\[\begin{split} \begin{align*} p_k(x) = c_{0, k} &+ c_{1, k}(x - x_{k-1}) \\ &+ c_{2, k} (x - x_{k-1})^2 + c_{3, k} (x - x_{k-1})^3. \end{align*} \end{split}\]

Slijedi da su druge derivacije jednake

\[\begin{split} \begin{align*} p_k''(x) &= 2c_{2, k} + 6c_{3, k} (x - x_{k-1}), \\ p_{k+1}''(x) &= 2c_{2, k+1} + 6c_{3, k+1} (x - x_{k}). \\ \end{align*} \end{split}\]

U obje derivacije uvrstimo \(x = x_k\), izjednačimo desne strane i podijelimo s 2:

(3.19)\[ c_{2, k} + 3 c_{3, k} (x_k - x_{k-1}) = c_{2, k+1}.\]

Podsjetimo se formula za \(c_{2, k}\), \(c_{3, k}\) koje smo ranije izveli (uz \(h_k = x_{k} - x_{k-1}\)):

\[\begin{split} \begin{align*} c_{3, k} &= \frac{s_k + s_{k-1} - 2f[x_{k-1}, x_k]}{h_k^2}, \\ c_{2, k} &= \frac{f[x_{k-1}, x_k] - s_{k-1}}{h_k} - h_k c_{3, k} \\ &= \frac{3f[x_{k-1}, x_k] - 2s_{k-1} - s_k}{h_k}, \end{align*} \end{split}\]

te ih uvrstimo u (3.19):

\[ \frac{-3f[x_{k-1}, x_k] + s_{k-1} + 2s_k}{h_k} = \frac{3f[x_{k}, x_{k+1}] - 2s_{k} - s_{k+1}}{h_{k+1}}. \]

Kako ovo mora vrijediti za \(k=1, 2, \ldots, n-1\), na kraju smo dobili ukupno \(n-1\) linearnu jednadžbu za nepoznanice \(s_0, \ldots, s_n\):

\[ \begin{align*} h_{k+1} s_{k-1} &+ 2(h_k + h_{k+1}) s_k + h_k s_{k+1} = 3(h_{k+1} f[x_{k-1}, x_k] + h_k f[x_k, x_{k+1}]). \end{align*} \]

Da bi \(s_0, \ldots, s_n\) bili jednoznačno određeni, možemo zadati neke fiksne vrijednosti od \(s_0\) i \(s_n\) i onda nam preostaje točno linearni sustav \(As = b\) za nepoznanice \(s_1, \ldots, s_{n-1}\).

Rješavanje sustava za \(s_1, \ldots, s_{n-1}\)

Uočimo da je matrica tog sustava

\[\begin{split} \mb{ccccc} 2(h_1 + h_2) & h_1 & & & \\ h_3 & 2(h_2 + h_3) & h_2 & & \\ & \ddots & \ddots & \ddots & \\ & & h_{n-1} & 2(h_{n-2} + h_{n-1}) & h_{n-2} \\ & & & h_n & 2(h_{n-1} + h_n) \me =: \mb{ccccc} d_1 & e_1 & & & \\ c_2 & d_2 & e_2 & & \\ & \ddots & \ddots & \ddots & \\ & & c_{n-1} & d_{n-1} & e_{n-2} \\ & & & c_n & d_n \me \end{split}\]

tridijagonalna i strogo dijagonalno dominantna po recima jer je očito \(2(h_k + h_{k+1}) > h_k + h_{k+1}\). Stoga je ta matrica regularna i uvijek ima LU-faktorizaciju (Teorem 2.10). Znamo i da su faktori u LU-faktorizaciji vrpčastih matrica ponovno vrpčaste matrice:

\[\begin{split} L = \mb{ccccc} 1 & & & & \\ \ell_1 & 1 & & & \\ & \ell_2 & 1 & & \\ & & \ell_3 & 1 & \\ & & & \ell_4 & 1 \me, \quad U = \mb{ccccc} u_1 & e_1 & & & \\ & u_2 & e_2 & & \\ & & u_3 & e_3 & \\ & & & u_4 & e_4 \\ & & & & u_5 \me, \end{split}\]

a lako se pokaže kako direktno izračunati brojeve \(\ell_i\) i \(u_i\) (uočite da su \(e_i\)-ovi u \(U\) posve isti kao u \(A\)):

u[1] = d[1];
for i in range( 2, n+1 ):
    l[i] = c[i] / u[i-1];
    u[i] = d[i] - l[i] * e[i-1];

Složenost LU-faktorizacije tridijagonalnih matrica je samo \(\bigO(n)\), a isto vrijedi i za rješevanje trokutastih sustava sa \(L\) i \(U\)!

Dokažite indukcijom i da su svi elementi \(\ell_i\), \(u_i\), \(e_i\) veći od nule, što smo već spomenuli u poglavlju o linearnim sustavima kod stabilnosti unatrag algoritma LU-faktorizacije (hint: pokažite da vrijedi \(u_i \geq \frac{i+1}{i}(h_i + h_{i+1})\)).

Iz gornje procedure vidimo da kod interpolacije kubičnim splajnom nagibi \(s_k\) nisu nezavisni, nego povezani sustavom linearnih jednadžbi. To znači da aproksimacija \(\varphi\) više nije lokalna, jer se promjenom jedne vrijednosti \(f(x_k)\) mijenjaju svi polinomi \(p_0, p_1, \ldots, p_n\)!

Izbor \(s_0\), \(s_n\).

Još preostaje definirati kako se biraju \(s_0\) i \(s_n\).

Tu postoji nekoliko standardnih pristupa:

1. „Potpuni splajn” – \(s_0 := f'(x_0)\), \(s_n := f'(x_n)\), tj. derivacija od \(f\) se koristi samo za \(x_0\) i \(x_n\).

2. „Prirodni splajn” – Definira se da mora vrijediti \(\varphi''(x_0) = \varphi''(x_n) = 0\), tj. \(p_0''(x_0)=0\), \(p_n''(x_n)=0\). Ovo ima primjenu kod nekih diferencijalnih jednadžbi. U općenitijem slučaju, mogu biti zadane i ne-nul druge derivacije u \(x_0\) i \(x_n\).

3. „Not-a-knot” – \(s_0\) i \(s_n\) namjestimo tako da vrijedi \(p_0 = p_1\) i \(p_{n-1} = p_n\).

Drugi i treći uvjet vode na dodatne dvije linearne jednadžbe, no sustav i dalje ostaje tridijagonalan i dijagonalno dominantan.

Za aproksimaciju periodičkih funkcija \(f\) je prirodno zahtijevati \(\varphi'(x_0) = \varphi'(x_n)\) i \(\varphi''(x_0) = \varphi''(x_n)\), tj. \(p_0'(x_0) = p_n'(x_n)\) i \(p_0''(x_0) = p_n''(x_n)\). U tom slučaju matrica sustava više neće biti tridijagonalna.

Za grešku kod splajn interpolacije mogu se pokazati vrlo slični rezultati kao kod po dijelovima kubične Hermiteove interpolacije. Na primjer, ako je \(f \in C^4([a, b])\), onda „not-a-knot” interpolacija \(\varphi\) zadovoljava

\[ \|f - \varphi\|_{\infty} \leq \frac{5}{384} h^4 \|f^{(4)}\|_{\infty}. \]

Iako kubičnu splajn interpolaciju možemo implementirati i sami (probajte!), jednostavnije je u Pythonu koristiti ugrađenu klasu CubicSpline iz biblioteke scipy.interpolate. Ona po defaultu koristi „not-a-knot”, no može se dodatnim parametrom konfigurirati i drugačije.

import numpy as np;
import scipy.interpolate as scin;

# Definiramo polje čvorova interpolacije. 
x = np.array( [-1, -0.5, 0, 0.5, 1] );

# Izračunamo vrijednosti funkcije f u tim čvorovima, npr. za f(x)=cos(x): 
y = np.cos(x);

# Sada možemo konstruirati kubičnu splajn interpolaciju phi.
# Uočite da nam ne trebaju derivacije od f!
phi = scin.CubicSpline( x, y );

# Objekt phi se sada ponaša kao obična funkcija.
print( 'f(0.25)   = ', np.cos(0.25) );
print( 'phi(0.25) = ', phi(0.25) );

f(0.25)   =  0.9689124217106447
phi(0.25) =  0.9684590136505103

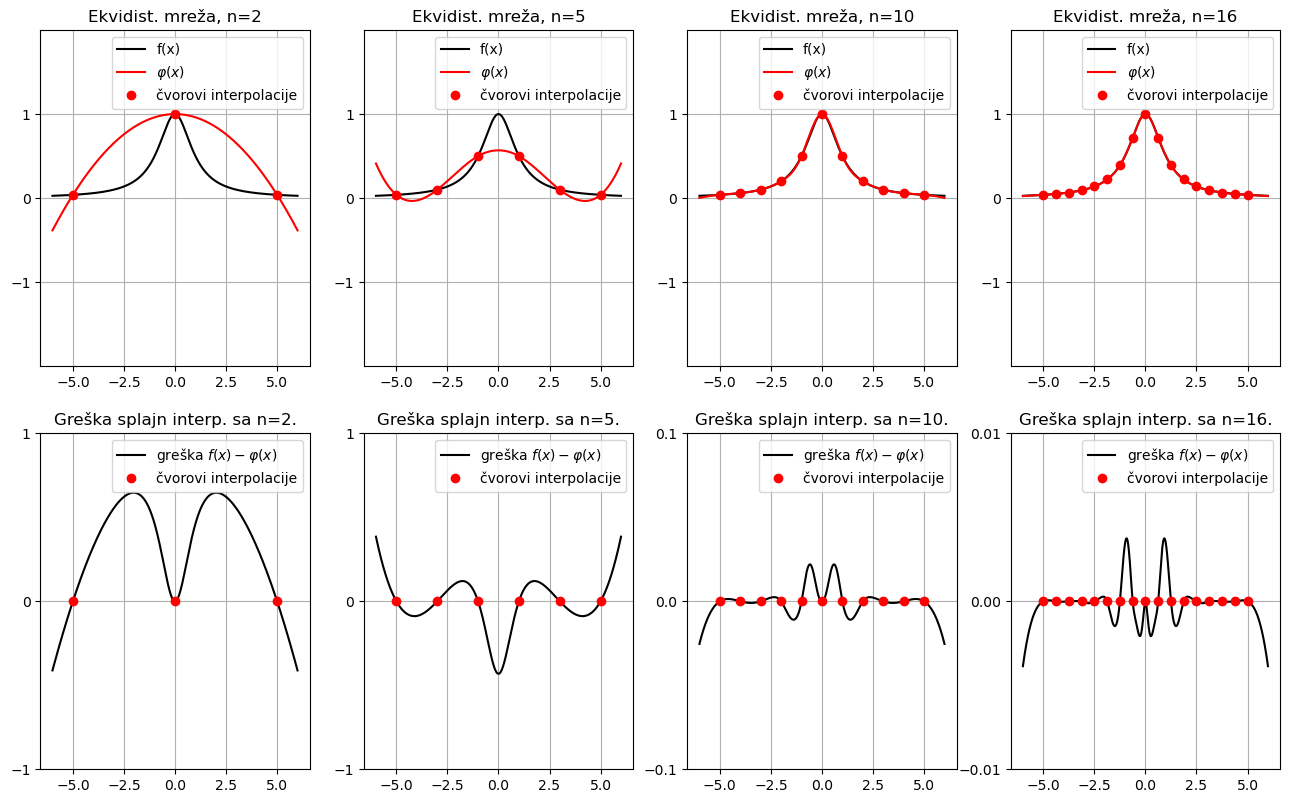
Primjer. Promotrimo ponovno funkciju Runge \(f(x) = \frac{1}{1+x^2}\) na intervalu \([-5, 5]\) i njezinu interpolaciju kubičnim splajnom. Koristimo ekvidistantnu mrežu redom s \(n=2, 5, 10, 16\) čvorova. Uočite da smanjujemo skalu na y-osi grafova greške!

Usporedite dobiveno sa svim ranijim interpolacijama.

Show code cell source Hide code cell source

import numpy as np;
import scipy.interpolate as scin;
import matplotlib.pyplot as plt;

def interpoliraj( n, graf ):
    # Čvorovi interpolacije: n+1 ekvidistantna točka između 0.1 i 1, uključujući rubove.
    x = np.linspace(-5, 5, num=n+1);

    # Vrijednosti funkcije f u čvorovima interpolacije.
    f = 1 / (1 + x * x);
    
    # Kubična splajn interpolacija phi pomoću biblioteke scipy.
    # Uočite da nam ne trebaju derivacije od f!
    phi = scin.CubicSpline(x, f);

    # Točke u kojima želimo izračunati vrijednost funkcije phi.
    # Uzet ćemo 1000 točaka u intervalu [-6, 6].
    xx = np.linspace(-6, 6, num=1000);

    # Evaluiramo phi u točkama xx.
    yy = phi(xx);

    # Vrijednosti funkcije Runge u točkama xx.
    ff = 1 / (1 + xx * xx);  

    # Nacrtamo graf kubičnog splajna i funkcije Runge, te čvorove interpolacije.
    plt.subplot( 2, 4, graf );
    plt.plot(xx, ff, 'k-', label='f(x)');
    plt.plot(xx, yy, 'r-', label='$\\varphi(x)$');
    plt.plot(x, f, 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();
    plt.ylim(-2, 2);
    plt.yticks(ticks=[0, -1, 1]);
    plt.title('Ekvidist. mreža, n=' + str(n));

    # Nacrtamo graf za grešku, te čvorove interpolacije.
    plt.subplot( 2, 4, 4+graf );
    plt.plot(xx, yy-ff, 'k-', label='greška $f(x)-\\varphi(x)$');
    plt.plot(x, np.zeros_like(x), 'ro', label='čvorovi interpolacije');

    plt.legend();
    plt.grid();

    if( n > 10 ):
        plt.ylim(-0.01, 0.01);
        plt.yticks(ticks=[0, -0.01, 0.01]);
    elif( n > 5 ):
        plt.ylim(-0.1, 0.1);
        plt.yticks(ticks=[0, -0.1, 0.1]);
    else:
        plt.ylim(-1, 1);
        plt.yticks(ticks=[0, -1, 1]);

    
    plt.title('Greška splajn interp. sa n=' + str(n) + '.');

plt.figure(figsize=[16, 9.6]);

interpoliraj(2, graf=1);
interpoliraj(5, graf=2);
interpoliraj(10, graf=3);
interpoliraj(16, graf=4);

Zašto ne po dijelovima kvadratna interpolacija?

Ako bi restrikcije od \(\varphi\) na \([x_{k-1}, x_k]\) bile kvadratni polinomi \(p_k\), onda:

• Za svaki \(p_k\) treba odrediti 3 koeficijenta.

• Uvjeti interpolacije u rubovima intervala daju 2 jednadžbe.

• Ne možemo postići da \(\varphi\) ima neprekidnu derivaciju jer bi to dodalo još po 2 uvjeta na \(p_k\), \(k=1, \ldots, n-1\)!

Zbog toga je takva interpolacija nepraktična i ne koristi se u praksi.