Show code cell source
import numpy as np;
import scipy as sc;
import matplotlib.pyplot as plt;
from scipy.linalg import solve_triangular;
from scipy.optimize import curve_fit;
%matplotlib inline
4.2. QR faktorizacija#
Zaključili smo da je sustav normalnih jednadžbi numerički loš način za rješavanje diskretnog problema najmanjih kvadrata. Osim toga, tvrdnja i dokaz Teorema 4.3 sugeriraju da je ključ u rješavanju ovog problema promatrati ortogonalnost vektora. Problem određivanja vektora \(x\in\R^m\) takav da je \(b - Ax = b - \sum_{i=1}^m x_i Ae_i\) okomit na \(\mathcal R (A)\) (\(e_i\) su ovdje vektori kanonske baze) ekvivalentan je problemu određivanja ortogonalne projekcije vektora \(b\) na \(\mathcal R (A)\). Problem ortogonalnih projekcija najlakše određujemo kada znamo ortonormiranu bazu za prostor u kojem tražimo projekciju.
To nas motivira da ortonormiramo stupce matrice \(A\), što se radi Gram-Schmidtovim postupkom. Uvodimo definiciju QR faktorizacije koja je zapravo matrični prikaz Gram-Schmidtovog postupka.
Neka je \(A \in \R^{n\times m}\), uz \(n\geq m\), matrica punog stupčanog ranga \(m\). Njezina QR faktorizacija je rastav oblika
pri čemu je \(Q \in \R^{n \times n}\) ortogonalna matrica, te \(R_0 \in \R^{m \times m}\) gornjetrokutasta matrica s pozitivnim elementima na dijagonali. Skraćeni zapis QR faktorizacije
pri čemu je \(Q_0\) dobivena od prvih \(m\) stupaca matrice \(Q\).
Označimo li matricu preostalih stupaca od \(Q\) s \(Q_1\), onda raspis
opravdava skraćeni zapis QR faktorizacije. Ona se u praksi češće koristi (pogotovo u problemu najmanjih kvadrata), jer ju je mnogo ekonomičnije izračunati i pohraniti od potpune faktorizacije kada je \(m \ll n\).
Svaka matrica \(A \in \R^{n\times m}\), uz \(n\geq m\) punog stupčanog ranga \(m\) dopušta QR faktorizaciju. Pri tome je skraćena QR faktorizacija jedinstvena.
Neka su \(a_1,a_2, \dots, a_m\) stupci matrice \(A\). Neka su vektori \(q_1,\dots,q_m\) dobiveni Gram-Schmidtovim postupkom primjenjenim na vektore \(a_1,a_2, \dots, a_m\): za svaki \(i=1,2,\dots, m\) vrijedi
Algoritam je dobro definiran, tj. nazivnik \(\|q'_i\|_2\) nikad nije jednak nuli. U suprotnom bi iz definicije imali da je skup \(\{ a_i, q_1, \dots, q_{i-1}\}\) linearno zavisan. Kako iz Gram-Schmidtovog postupka znamo da je \([\{q_1, \dots, q_{i-1}\}] = [\{a_1, \dots, a_{i-1}\}]\), ovime bismo dobili da stupci matrice \(A\) nisu punog ranga, što dovodi do kontradikcije.
Definirajmo matricu \(Q_0\) tako da vektore \(q_1,\dots,q_m\) poslažemo u stupce. Ti stupci međusobno su okomiti i norme su \(1\), pa je matrica \(Q_0\) traženog oblika. Definirajmo matricu \(R_0:= Q_0^T A \in \R^{m\times m }\), odnosno da za nju vrijedi \(A = Q_0 R_0\).
Usporedbom svakog elementa \((i,j)\) matrice \(R_0\), dobivamo da je nužno da za elemente te matrice vrijedi \(r_{i,j} = \langle q_i, a_j \rangle\). S druge strane, iz definicije za \(q'_i\) iz Gram-Schmidtovog postupka dobivamo
Gornju relaciju množimo s nekim vektorom \(q_i\) i koristimo ortonormiranost tih vektora. Množenjem gornje relacije s \(q_j\) dobivamo \(r_{j,j} = \langle q_j, a_j \rangle = \| q'_j\| >0\). Množenjem gornje relacije s \(q_i\) (pri čemu je \(i>j\)) dobivamo \(r_{i,j} = \langle q_i, a_j \rangle = 0\). To dokazuje da je matrica \(R_0\) gornjetrokutasta s pozitivnim elementima na dijagonali.
Ovime smo dokazali egzistenciju skraćene QR faktorizacije. Za punu QR faktorizaciju samo matricu \(Q_0\) nadopunimo do kvadratne ortogonalne.
Ključni razlog da je matrica \(R\) gornjetrokutasta je u tome što je posljedica Gram-Schmidtovog postupka da za svaki \(k=1,2,\dots,n\) vrijedi da je \([\{a_1,a_2, \dots, a_n\}] = [\{q_1,q_2,\dots,q_n\}]\).
Napomenimo još da se u računalu QR faktorizacija najčešće ne računa Gram-Schmidtovim postupkom nego Givensovim rotacijama ili Householderovim reflektorima. Za detalje ovih algoritama, pogledajte članak na Wikipediji.
Rješavanje diskretnog problema najmanjih kvadrata QR faktorizacijom#
Pokažimo sada precizno ono što smo motivirali na početku ovog poglavlja: kako QR faktorizaciju iskoristiti u rješavanju problema najmanjih kvadrata.
Poznato je da je norma \(2\) unitarno invarijantna, odnosno, za svaku ortogonalnu matricu \(U\) i bilo koji vektor \(x\) odgovarajuće duljine vrijedi
Neka su \(A\) i \(b\) matrica i vektor iz problema najmanjih kvadrata i neka je
QR faktorizacija matrice \(A\). Imamo redom
Na drugi član ne možemo utjecati jer ne ovisi o \(x\). U prvom imamo regularnu gornjetrokutastu matricu \(R_0\) reda \(m\), nepoznati vektor \(x\) duljine \(m\) i poznati vektor \(Q_0^Tb\) duljine \(m\). Taj član će biti najmanji moguć kada je on jednak nuli, što je moguće jer sustav \(R_0x = Q_0^T b\) ima jedinstveno rješenje (dapače, jednostavno ga je naći povratnom supstitucijom).
Time smo dokazali da je
te se taj minimum postiže za \(x\) koji je rješenje sustava \(R_0x = Q_0^T b\).
Pokažimo i kod u Pythonu za rješenje Primjera 4.1 korištenjem QR faktorizacije.
Show code cell source
def QRLinearniNajmanjiKvadrati (x,y):
# Izrada sustava jednadžbi
n = len(x)
A = np.zeros((n, 2))
A[:, 0] =x[:]
A[:, 1] = np.ones(n)
B = y
# Rješavanje sustava
Q, R = np.linalg.qr(A, mode='reduced')
rj = solve_triangular(R , Q.T @ B, lower=False)
a = rj[0]
b = rj[1]
return a, b
# Zadani podaci
x = np.array([1, 2, 3, 4, 5])
y = np.array([2.5, 3.7, 3.5, 4.5, 4.9])
a, b = QRLinearniNajmanjiKvadrati(x, y)
# Ispis rezultata
print("Vrijednost a:", a)
print("Vrijednost b:", b)
Vrijednost a: 0.56
Vrijednost b: 2.1399999999999992
Show code cell source
# Dio koda za vizualizaciju
def model(x, a, b):
return a * x + b
x_line = np.linspace(min(x), max(x), 100)
y_line = model(x_line, a, b)
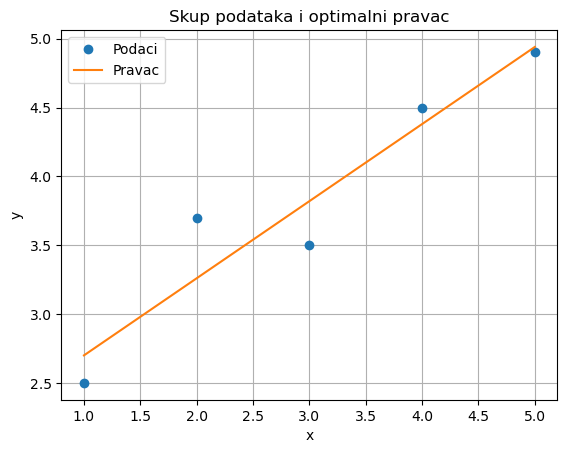
plt.plot(x, y, 'o', label='Podaci')
plt.plot(x_line, y_line, label='Pravac')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Skup podataka i optimalni pravac')
plt.legend()
plt.grid(True)
plt.show()