3. Kriptosustavi s javnim ključem

3.1. Ideja javnog ključa

Godine 1976. Whitfield Diffie i Martin Hellman su ponudili jedno moguće rješenje problema razmjene ključeva, zasnovano na činjenici da je u nekim grupama potenciranje puno jednostavnije od logaritmiranja.

Pretpostavimo da se osobe A i B žele dogovoriti o jednom tajnom slučajnom elementu u cikličkoj grupi G, kojeg bi onda poslije mogli koristi kao ključ za šifriranje u nekom simetričnom kriptosustavu. Oni taj svoj dogovor moraju provesti preko nekog nesigurnog komunikacijskog kanala, bez da su prethodno razmijenili bilo kakvu informaciju. Jedina informacija koju imaju jest grupa G i njezin generator g.

Diffie-Hellmanov protokol za razmjenu ključeva: Osoba A generira slučajan prirodan broj a ∈ {1, 2, ... , |G| - 1}. Ona pošalje osobi B element ga. Osoba B generira slučajan prirodan broj b ∈ {1, 2, ... , |G| - 1}, te pošalje osobi A element gb. Osoba A izračuna (gb)a = gab. Osoba B izračuna (ga)b = gab. Sada je njihov tajni ključ K = gab.

Njihov protivnik koji može prisluškivati njihovu komunikaciju preko nesigurnog komunikacijskog kanala zna sljedeće podatke: G, g, g^a, g^b, te treba iz ovih podataka izračunati g^ab. Ako protivnik iz poznavanja g i g^a može izračunati a (tj. ako može riješiti problem diskretnog logaritma), onda i on može pomoću a i g^b izračunati g^ab.

Diffie i Hellman se smatraju začetnicima kriptografije javnog ključa. Ideja javnog ključa se sastoji u tome da se konstruiraju kriptosustavi kod kojih bi iz poznavanja funkcije šifriranja e_K bilo praktički nemoguće (u nekom razumnom vremenu) izračunati funkciju dešifriranja d_K. Tada bi funkcija e_K mogla biti javna. U provedbi ove ideje ključnu ulogu igraju tzv. osobne jednosmjerne funkcije. Za funkciju f kažemo da je jednosmjerna (one-way) ako je f lako, a f ^-1 teško izračunati. Ako je pritom f ^-1 lako izračunati ukoliko nam je poznat neki dodatni podatak (trapdoor - skriveni ulaz), onda f nazivamo osobna jednosmjerna funkcija. Uočimo da se i u klasičnoj kriptografiji tajnost u suštini zahtijeva samo od funkcije za dešifriranje d_K. Banalan primjer: kod Cezarove šifre nije problem što svi znaju da se slova šifriraju tako da se pomiču za 3 mjesta udesno, već je problem što iz tog podatka baš svatko može zaključiti da se dešifriranje provodi pomicanjem za 3 mjesta ulijevo. No, i kod svih ostalih kriptosustava koje smo dosad susreli, veza funkcija e_K i d_K je bila vrlo jednostavna, pa skrivanje jedne, a otkrivanje druge funkcije nije imalo nikakvog smisla.

Kriptosustav s javnim ključem se sastoji od dviju familija {eK} i {dK} funkcija za šifriranje i dešifriranje (ovdje K prolazi skupom svih mogućih korisnika) sa svojstvom: Za svaki K je dK inverz eK. Za svaki K je eK javan, ali je dK poznat samo osobi K. Za svaki K je eK osobna jednosmjerna funkcija. eK se zove javni ključ, a dK tajni ili osobni ključ.

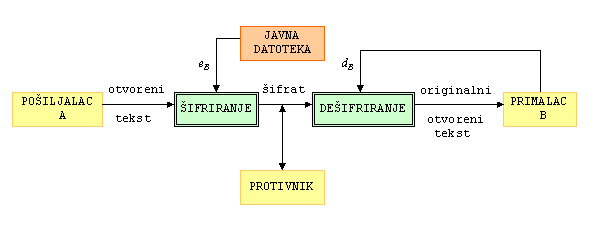
Ako pošiljalac A želi poslati poruku x primaocu B, onda B najprije pošalje A svoj javni ključ e_B. Potom A šifrira svoju poruku pomoću e_B i pošalje primaocu šifrat y = e_B(x). Konačno, B dešifrira šifrat koristeći svoj tajni ključ d_B:   d_B(y) = d_B(e_B(x)) = x.

Ukoliko grupa korisnika želi komunicirati na ovaj način, situacija je još jednostavnija. Naime, tada svi korisnici stave svoje javne ključeve u neku javnu, svima dostupnu datoteku. Sada B ne mora slati svoj javni ključ osobi A, već A jednostavno pročita e_B iz datoteke.

Ovdje se može postaviti pitanje kako osoba B može biti sigurna da joj je upravo osoba A poslala poruku. Naime, svatko ima pristup funkciji e_B, pa se može lažno predstaviti kao osoba A. Dakle, postavlja se pitanje vjerodostojnosti ili autentičnosti poruke. To se može riješiti na sljedeći način:

• A doda svojoj poruci slučajan broj a od recimo 10 znamenaka.
• B generira svoj slučajan 10-znamenkasti broj b, te pošalje osobi A poruku e_A(a + b).
• A izračuna b pomoću formule b = d_A(e_A(a + b)) - a, te sada ponovo pošalje svoju prvu poruku tako da joj doda b, a isto to učini i sa svakom idućom porukom koju će slati osobi B.

Neki kriptosustavi omogućavaju čak da korisnici digitalno potpišu svoju poruku. To je važno zbog toga što tada A ne može kasnije zanijekati da je upravo on poslao konkretnu poruku. Pretpostavimo da je P = C. Tada A može potpisati poruku x tako da osobi B pošalje šifrat z = d_A(y) = d_A(e_B(x)). Kad B primi poruku za koju pretpostavlja da mu je poslao A, on najprije primijeni javni ključ e_A, a potom svoj tajni ključ d_B:

d_B(e_A(z)) = d_B(e_A(d_A(e_B(x)))) = x.

Glavne prednosti kriptosustava s javnim ključem u usporedbi sa simetričnima su:

• nema potrebe za sigurnim komunikacijskim kanalom za razmjenu ključeva
• za komunikaciju grupe od N ljudi treba 2N ključeva, za razliku od N(N-1)/2 ključeva kod simetričnog kriptosustava
• mogućnost potpisa poruke

Pa ipak, u realnom svijetu kriptografija javnog ključa ne predstavlja zamjenu za simetrične kriptosustave. Ona se ne koristi za šifriranje poruka, već za šifriranje ključeva. Naime, osobe A i B komuniciraju pomoću simetričnog kriptosustava s ključem kojeg su razmijenili pomoću kriptosustava s javnim ključem. To se zove hibridni kriptosustav.

Osnovni razlog zašto se javni ključ ne koristi za šifriranje poruka, jest da su algoritmi s javnim ključem puno sporiji (oko 1000 puta) od modernih simetričnih algoritama.

Drugi nedostatak kriptosustava s javnim ključem jest da su slabi na napad "odabrani otvoreni tekst". Ako je y = e(x), gdje otvoreni tekst može poprimiti jednu od n vrijednosti, onda, budući je e javna, kriptoanalitičar treba samo šifrirati svih n mogućih otvorenih tekstova i rezultat usporediti s y. Tako neće otkriti tajni ključ d, ali će otkriti otvoreni tekst x. Jasno, ovaj napad je primjenjiv ako je n mali (npr. ako je x neki iznos u kunama za kojeg je razumno pretpostaviti da je manji od 1000000).

U modernoj kriptografiji, koja se koristi u komercijalnom svijetu (tipična situacija je da osoba A želi kupiti nešto od osobe B preko interneta), pojavljuju se, uz klasične, i neki sasvim novi problemi:

1. POVJERLJIVOST (confidentiality): Poruku koju osoba A šalje osobi B ne može pročitati nitko drugi.
2. VJERODOSTOJNOST (autenticity): Osoba B zna da je samo osoba A mogla poslati poruku koju je ona upravo primila.
3. NETAKNUTOST (integrity): Osoba B zna da poruka koju je poslala osoba A nije promijenjena prilikom slanja.
4. NEPOBITNOST (non-repudiation): Osoba A ne može kasnije zanijekati da je poslala poruku.

Kako smo već rekli, kriptosustavi javnog ključa su mnogo sporiji od simetričnih. Stoga je njihova uporaba u 1. problemu ograničena na razmjenu ključeva za simetrične šifre. S druge strane, "digitalni potpisi", koji se koriste u rješavanju 2., 3. i 4. problema, zahtijevaju uporabu kriptografije javnog ključa.