2.7. Advanced Encryption Standard

1. mora biti simetričan

2. mora biti blokovni

3. treba raditi sa 128-bitnim blokovima i ključevima s tri duljine: 128, 192 i 256 bitova.

• 3DES koristi 48 rundi da bi postigao sigurnost za koju je vjerojatno dovoljno 32 runde.
• Softverske implementacije 3DES-a su prespore za neke primjene, posebno za digitalne video podatke.
• 64-bitni blokovi nisu najefikasniji u nekim primjenama.

Natječaj je zaključen 15.6.1998. Od 21 pristigle prijave, 15 ih je zadovoljilo NIST-ove kriterije. U kolovozu 1999. NIST je objavio 5 finalista: MARS, RC6, RIJNDAEL, SERPENT i TWOFISH. Recimo nekoliko riječi o ovih 5 finalista.

MARS (IBM), RC6 (RSA Security Inc.) i TWOFISH (Counterpane Systems) spadaju u Feistelove šifre. Podsjetimo se da je Feistelova šifra blokovna šifra u kojoj u i-toj rundi koriste formule L_i = R_{i -1}, R_i = L_{i -1} ⊕ f (R_{i -1}, K_i) (dakle, isto kao kod DES-a). MARS spada u nebalansirane Feistelove šifre jer se blokovi ne dijele na 2, već na 4 dijela. MARS ima 32 runde, RC6 ima 20 rundi, dok TWOFISH ima 16 rundi. Specifičnost kriptosustava RC6 (koji je dosta sličan RC5) su korištenje funkcije f(x) = x(2x+1), koja daje difuziju, te rotacija ovisnih o podacima, koje daju otpornost na diferencijalnu i linearnu kriptoanalizu. Specifičnost TWOFISH-a je da se S-kutije dinamički mijenjaju u ovisnosti o ključu, što komplicira diferencijalnu i linearnu kriptoanalizu.

SERPENT su konstruirali kriptografi iz Engleske, Izraela i Danske. Spada u supstitucijsko-permutacijske šifre. Ima 32 runde i, što je za njega specifično, u svakoj rundi paralelno koristi 32 identične S-kutije.

RIJNDAEL su razvili belgijski kriptografi. Razlikuje se od ostalih finalista po tome što se u konstrukciji S-kutija koriste operacije u konačnom polju GF(2⁸).

Konačno, 2.8.2000. objavljeno je da je pobjednik natječaja za AES RIJNDAEL (čitaj: rejn dol). RIJNDAEL su razvili belgijski kriptografi Joan Daemen i Vincent Rijmen s Katoličkog sveučilišta Leuven, po kojima je i dobio ime.

Kako smo već napomenuli, jedna od njegovih specifičnosti je korištenje konačnog polja GF(2⁸) (alternativna oznaka je F_2⁸). Preciznije, elementi od GF(2⁸) su polinomi oblika a₇x⁷ + a₆x⁶ + ... + a₁x + a₀, a_i ∈ {0, 1}, a operacije su zbrajanje i množenje polinoma iz Z₂[X] modulo fiksni ireducibilni polinom g(x) = x⁸ + x⁴ + x³ + x + 1. Dakle, uzimamo da je GF(2⁸) = Z₂[X] / (g(x)). Elemente od GF(2⁸) možemo prikazati i kao bajtove (nizove od 8 bitova). Npr. polinomu x⁶ + x⁴ + x² + x + 1 odgovara bajt 01010111 ili 57 u heksadecimalnom zapisu.

Primjer 7: Pomnožiti polinome x⁶ + x⁴ + x² + x + 1 i x⁷ + x + 1 iz polja GF(2⁸).

Najprije pomnožimo ova dva polinoma u prstenu Z₂[X]:

(x⁶ + x⁴ + x² + x + 1) · (x⁷ + x + 1) = x¹³ + x¹¹ + x⁹ + x⁸ + x⁶ + x⁵ + x⁴ + x³ + 1.

U RIJNDAEL-u se također koriste i operacije na polinomima s koeficijentima iz GF(2⁸) stupnja manjeg od 4. Svaki takav polinom možemo reprezentirati kao 4-bajtni vektor. Zbrajanje takvih polinoma se svodi na zbrajanje koeficijenta uz iste potencije (zbrajanje u GF(2⁸) smo već definirali). Da bi kod množenja dobili kao rezultat polinom stupnja manjeg od 4, moramo produkt reducirati modulo neki polinom četvrtog stupnja. U RIJNDAEL-u je za to izabran polinom X⁴ + 1. Polinom X⁴ + 1 je izabran da bi množenje bilo što jednostavnije za implementirati. Pritom polinom X⁴ + 1 nije ireducibilan nad Z₂[X], jer u Z₂[X] vrijedi: X⁴+1=(X+1)⁴. Stoga neće svi polinomi imati inverz. No, to ovdje nije ni nužno. Zapravo, vidjet ćemo da se postojanje inverza zahtijeva samo za jedan konkretan polinom, za kojeg ćemo postojanje inverza provjeriti u sljedećem primjeru. Uz ovaj izbor, množenje polinoma se može matrično zapisati ovako:

d0 d1 d2 d3

=

a0 a3 a2 a1 a1 a0 a3 a2 a2 a1 a0 a3 a3 a2 a1 a0

b0 b1 b2 b3

Ovdje je polinom d(X) = d₃X³ + d₂X² + d₁X+ d₀ rezultat množenja polinoma a(X) = a₃X³ + a₂X² + a₁X+ a₀ i b(X) = b₃X³ + b₂X² + b₁X+ b₀, u oznaci d(X) = a(X) ⊗ b(X).

Primjer 8: Izračunati:

(03 X³ + 01 X² + 01 X + 02) ⊗ (0B X³ + 0D X² + 09 X + 0E).

d₃ = 03 · 0E + 01 · 09 + 01 · 0D + 02 · 0B.

03 · 0E = (x + 1) · (x³ + x² + x) = x⁴ + x = 12,

01 · 09 = 09,       01 · 0D = 0D,

02 · 0B = x · (x³ + x + 1) = x⁴ + x² + x = 16.

d₃ = 12 + 09 + 0D + 16 = (x⁴ + x) + (x³ + 1) + (x³ + x² + 1) + (x⁴ + x² + x) = 00.

RIJNDAEL šifrira blokove od 128 bitova = 16 bajtova. Svaki takav blok se može shvatiti kao 16 elemenata polja, koji se reprezentiraju pomoću 4 × 4 matrice s elementima iz GF(2⁸). Tu matricu ćemo zvati aes-blok. Ključ također ima 128 bitova (postoje i varijante sa 192 i 256 bitova). RIJNDAEL ima 10 rundi (uz 128-bitni ključ). Svaka runda se sastoji od 4 operacije:

        SubBytes
        ShiftRows
        MixColumns
        AddRoundKey

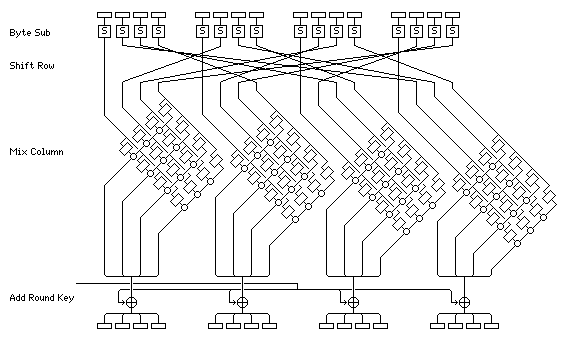
Prije prve runde vrši se inicijalno dodavanje ključa (AddRoundKey), a u posljednjoj rundi se izostavlja transformacija MixColumns. Jedna runda AES-a ilustrirana je na slici (prema [Savard: A Cryptographic Compendium]).

1. svaki element aes-bloka (matrice) se zamjeni svojim inverzom u GF(2⁸) (s time da element 00, jedini koji nema inverz, ostaje nepromijenjen),

2. primjeni se fiksna afina transformacija

   b'_i = b_i ⊕ b_{(i+4) mod 8} ⊕ b_{(i+5) mod 8} ⊕ b_{(i+6) mod 8} ⊕ b_{(i+7) mod 8} ⊕ c_i,

   gdje je c = 01100011.

ShiftRows - ciklički pomiče elemente i-tog retka aes-bloka za i mjesta ulijevo (i = 0,1,2,3).

MixColumns - Stupci matrice se shvate kao polinomi nad GF(2⁸). Dakle, stupac A_i = (a_0i, a_1i, a_2i, a_3i) se shvati kao polinom a_3iX³ + a_2iX² + a_1iX + a_0i. Sada se ti polinomi pomnože s polinomom 03 X³ + 01 X² + 01 X + 02 (u skladu s ranije definiranim operacijama nad polinomima, rezultat se računa modulo X⁴ + 1).

AddRoundKey je XOR aes-bloka s međuključem koji odgovara trenutnoj rundi.

S-kutije (operacija ByteSub) su dizajnirane tako da bi kriptosustav bio što otporniji na diferencijalnu i linearnu kriptoanalizu, dok su ShiftRow i MixColumn zaslužni za difuziju.

U konstrukciji međuključeva se najprije ključ proširi korištenjem XOR-a i cikličkog pomaka. Prošireni ključ se sastoji od 44 riječi (4-bajtnih vektora). Međuključevi se biraju iz proširenog ključa tako da se prvi međuključ sastoji od prve četiri riječi, drugi od sljedeće četiri, itd.

Preostalo je još opisati malo detaljnije postupak proširivanja ključa. Prve 4 riječi proširenog ključa predstavlja zadani ključ. Svaku sljedeću riječ r_i dobijemo iz prethodne riječi r_{i -1} tako da primijenimo XOR s r_{i -4}. Ako je i višekratnik od 4, onda prije operacije XOR izvršimo operacije RotWord (rotira riječ jedno mjesto ulijevo, tj. [r₀r₁r₂r₃] promijeni u [r₁r₂r₃r₀]), SubWord (uzima jedan po jedan bajt iz riječi i na svakog od njih primjeni S-kutiju), te XOR s riječi [02^{(i -4)/4},00,00,00].

Dešifriranje se odvija po istom algoritmu kao i šifriranje, osim što se umjesto transformacija ByteSub, ShiftRow i MixColumn koriste njihovi inverzi. Primijetimo da smo u Primjeru 8 dokazali da polinom 03 X³ + 01 X² + 01 X + 02 ima inverz 0B X³ + 0D X² + 09 X + 0E (svi ostali dijelovi algoritma za šifriranje su očito invertibilni).