 3 + 1 = 22,
1
3 + 1 = 22,
1  120 + 1 = 112,
120 + 1 = 112, 1
 8 + 1 = 32,
3
8 + 1 = 32,
3  120 + 1 = 192,
120 + 1 = 192, 3
 8 + 1 = 52,
8
8 + 1 = 52,
8  120 + 1 = 312.
120 + 1 = 312.
Prvu racionalnu Diofantovu četvorku pronašao je grčki matematičar Diofant, po kome su ovi skupovi i dobili ime. Ta četvorka je bila
{1/16, 33/16, 17/4, 105/16}.
Prvu (cjelobrojnu) Diofantovu četvorku, skup{1, 3, 8, 120},
pronašao je Fermat. Uvjerimo se da je ovaj skup zaista Diofantova četvorka:
1  3 + 1 = 22,
1
3 + 1 = 22,
1  120 + 1 = 112,
120 + 1 = 112,
1  8 + 1 = 32,
3
8 + 1 = 32,
3  120 + 1 = 192,
120 + 1 = 192,
3  8 + 1 = 52,
8
8 + 1 = 52,
8  120 + 1 = 312.
120 + 1 = 312.
{11/192, 35/192, 155/27, 512/27, 1235/48, 180873/16},
koji je pronašao Gibbs.Nedavno je dokazano da ne postoji niti jedna (cjelobrojna) Diofantova šestorka, a slutnja je da ne postoji niti Diofantova petorka. S druge strane, ne zna se nikakva gornja ograda za veličinu racionalnih Diofantovih m-torki.
Recimo nešto o vezi Diofantovih m-torki i eliptičkih krivulja. Pretpostavimo da želimo (cjelobrojnu ili racionalnu) Diofantovu trojku {a, b, c} nadopuniti do Diofantove četvorke. To znači da želimo naći broj d takav da su brojevi ad + 1, bd + 1 i cd + 1 potpuni kvadrati. Ovom problemu na prirodan način možemo pridružiti eliptičku krivulju
E : y2 = (x + ab)(x + ac)(x + bc).
Naime, ako je d rješenje našeg problema, onda je točka s prvom koordinatom x = abcd racionalna točka na krivulji E. Krivulja E ima tri racionalne točke reda 2: (-ab, 0), (-ac, 0), (-bc, 0), a također i trivijalnu racionalnu točku P = (0, abc) za koju nije teško pokazati da je beskonačnog reda. Dakle, na krivulji E postoji beskonačno mnogo racionalnih točaka (x, y). Postavlja se pitanje za koje će od tih točaka broj d = x / abc prestavljati rješenje polaznog problema, tj. imati svojstvo da je {a, b, c, d} racionalna Diofantova četvorka. Odgovor je da su to sve točke oblika P + [2] U, gdje je U proizvoljna racionalna točka na E. Na krivulji E se nalazi još jedna zanimljiva racionalna točka, naime točka s prvom koordinatom jednakom 1. Preciznije, ako jeab + 1 = r2, ac + 1 = s2, bc + 1 = t2,
onda točka S = (1, rst) leži na E. Štoviše, vrijedi da je S = [2] R, gdje jeR = ((rs + rt + st + 1), (r + s)(r + t)(s + t)).
Direktni račun pokazuje da su prve koordinate točaka P - S i P + S jednake
a + b + c
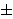 2abc + 2rst,
2abc + 2rst,
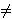 8,
može na točno dva načina proširiti do Diofantove četvorke.
8,
može na točno dva načina proširiti do Diofantove četvorke.
U dokazu da se svaka Diofantova četvorka može nadopuniti do
racionalne Diofantove petorke, ponovo se koristi pribrajanje i
oduzimanje točke S. Neka je T = (x, y)
točka na E takva da broj d = x / abc
zadovoljava uvjet da su ad + 1, bd + 1 i
cd + 1 potpuni kvadrati. Promotrimo točku T
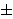 S = (x', y'). Tada broj d' =
x' / abc također zadovoljava isti uvjet kao i d.
No, vrijedi i više. Naime,
d
S = (x', y'). Tada broj d' =
x' / abc također zadovoljava isti uvjet kao i d.
No, vrijedi i više. Naime,
d  d' + 1
je također potpun kvadrat. Drugim riječima, {a, b,
c, d, d'} je racionalna Diofantova petorka.
Primjenom ove konstrukcije na Fermatov skup
{a, b, c, d} = {1, 3, 8, 120},
dobiva se upravo Eulerovo rješenje
d' = 777480 / 8288641.
d' + 1
je također potpun kvadrat. Drugim riječima, {a, b,
c, d, d'} je racionalna Diofantova petorka.
Primjenom ove konstrukcije na Fermatov skup
{a, b, c, d} = {1, 3, 8, 120},
dobiva se upravo Eulerovo rješenje
d' = 777480 / 8288641.
Više informacija o različitim problemima vezanim uz Diofantove m-torke može se naći na web stranici o Diofantovim m-torkama.
| Web stranica seminara | Andrej Dujella - osobna stranica |