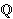 je
Mordell-Weilov teorem.
je
Mordell-Weilov teorem.
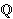 .
Kod takvih krivulja su, po definiciji, koeficijenti kubnog
polinoma racionalni brojevi. Međutim, množenjem s njihovim
zajedničkim nazivnikom možemo postići da su koeficijenti
cijeli brojevi. To znači da možemo pretpostaviti da naša
krivulja ima oblik
.
Kod takvih krivulja su, po definiciji, koeficijenti kubnog
polinoma racionalni brojevi. Međutim, množenjem s njihovim
zajedničkim nazivnikom možemo postići da su koeficijenti
cijeli brojevi. To znači da možemo pretpostaviti da naša
krivulja ima oblik
y2 = x3 + ax + b,
gdje su a, b cijeli brojevi i vrijedi da je 4a3 + 27b2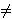 0.
0.
Najvažnija činjenica o eliptičkim krivuljama nad
 je
Mordell-Weilov teorem.
je
Mordell-Weilov teorem.
Teorem: (Mordell -
Weil)
E(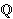 ) je konačno
generirana abelova grupa. ) je konačno
generirana abelova grupa.
|
Drugim riječima, postoji konačan skup racionalnih točaka
P1, ... , Pk iz kojih se
sve ostale racionalne točke na E mogu
dobiti metodom sekante i tangente.
Kako je svaka konačno generirana abelova grupa izomorfna
produktu cikličkih grupa, dobivamo sljedeću neposrednu
posljedicu Mordell-Weilovog teorema.
Korolar:
E(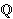 ) )
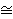 E(
E(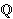 )tors × )tors ×
|
Grupa E(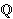 )tors koja se sastoji od svih
točaka konačnog reda naziva se torzijska grupa od E,
a nenegativni cijeli broj r
se naziva rang od E i označava se s rank (E).
)tors koja se sastoji od svih
točaka konačnog reda naziva se torzijska grupa od E,
a nenegativni cijeli broj r
se naziva rang od E i označava se s rank (E).
Korolar nam kaže da postoji r racionalnih točaka
P1, ... , Pr
na krivulji E sa svojstvom da se svaka racionalna
točka P na E može prikazati u obliku
P = T + m1P1 + ... + mrPr,
gdje je T neka točka konačnog reda, a m1, ... , mr cijeli brojevi.
Postavlja se pitanje koje sve vrijednosti mogu poprimiti
E(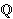 )tors
i rank (E). Nadalje, pitanje je kako izračunati te
vrijednosti za konkretnu krivulju E.
Pokazuje se da je puno lakše dati odgovore na ova pitanja
za torzijsku grupu, nego za rang. Do danas nije poznato koje
sve vrijednosti može poprimiti rang eliptičke krivulje. Vjeruje
se da rang može biti proizvoljno velik, no danas se zna tek da
postoji eliptička krivulja ranga
)tors
i rank (E). Nadalje, pitanje je kako izračunati te
vrijednosti za konkretnu krivulju E.
Pokazuje se da je puno lakše dati odgovore na ova pitanja
za torzijsku grupu, nego za rang. Do danas nije poznato koje
sve vrijednosti može poprimiti rang eliptičke krivulje. Vjeruje
se da rang može biti proizvoljno velik, no danas se zna tek da
postoji eliptička krivulja ranga
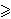 24
(Martin i
McMillen).
Krivulja najvećeg ranga za koju je rang egzaktno izračunan
(a ne samo donja ograda za rang) je krivulja ranga 15
(Dujella). (Naknadna napomena:
Elkies je 2005. godine pronašao
krivulju egzaktnog ranga 17, a 2006. godine krivulju ranga
24
(Martin i
McMillen).
Krivulja najvećeg ranga za koju je rang egzaktno izračunan
(a ne samo donja ograda za rang) je krivulja ranga 15
(Dujella). (Naknadna napomena:
Elkies je 2005. godine pronašao
krivulju egzaktnog ranga 17, a 2006. godine krivulju ranga
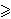 28.)
S druge strane,
Mazur je dokazao da postoji
točno 15 mogućih torzijskih grupa. To su
28.)
S druge strane,
Mazur je dokazao da postoji
točno 15 mogućih torzijskih grupa. To su

 ,
za n = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ili 12;
,
za n = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ili 12;

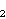 ×
×

 ,
za n = 2, 4, 6 ili 8.
,
za n = 2, 4, 6 ili 8.
 3. Podatci o najvećim poznatim rangovima za svaku od
15 mogućih torzijskih grupa mogu se naći u sljedećoj
tablici.
3. Podatci o najvećim poznatim rangovima za svaku od
15 mogućih torzijskih grupa mogu se naći u sljedećoj
tablici.
Recimo sada nešto o računanju torzijske grupe od E.
Pretpostavimo najprije
da je P = (x, y) točka reda 2
na E. To znači da je [2] P =
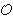 , odnosno
P = -P. No, odavde je (x, y) =
(x, -y), što povlači y = 0. Dakle, točke reda 2
su upravo točke s y-koordinatom jednakom 0. Možemo
imati 0, 1 ili 3 takve točke, što ovisi o broju racionalnih
nultočaka polinoma x3 + ax + b.
Te točke, zajedno s točkom u beskonačnosti
, odnosno
P = -P. No, odavde je (x, y) =
(x, -y), što povlači y = 0. Dakle, točke reda 2
su upravo točke s y-koordinatom jednakom 0. Možemo
imati 0, 1 ili 3 takve točke, što ovisi o broju racionalnih
nultočaka polinoma x3 + ax + b.
Te točke, zajedno s točkom u beskonačnosti
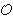 , čine podgrupu od
E(
, čine podgrupu od
E(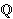 )tors koja je ili trivijalna
ili jednaka
)tors koja je ili trivijalna
ili jednaka 
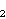 ili jednaka
ili jednaka

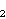 ×
×

 .
Ostale točke konačnog reda možemo naći korištenjem sljedećeg teorema.
.
Ostale točke konačnog reda možemo naći korištenjem sljedećeg teorema.
Teorem: (Lutz -
Nagell)
Ako je P = (x, y)
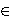 E(
E(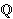 )tors,
onda su x i y cijeli brojevi, te vrijedi da je
ili y = 0 (tada P ima red 2) ili y2
dijeli diskriminantu D = - 4a3 -
27b2. )tors,
onda su x i y cijeli brojevi, te vrijedi da je
ili y = 0 (tada P ima red 2) ili y2
dijeli diskriminantu D = - 4a3 -
27b2.
|
Primjer: Odredite torzijsku grupu eliptičke krivulje
E : y2 = x3 + x.
Imamo D = -4. Stoga svaka torzijska točka P = (x, y) mora zadovoljavati ili y = 0 ili y | 2. Dakle, y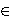 {0, 1, -1, 2, -2}. Lako se vidi da jednadžbe
x3 + x = 1 i x3 + x
= 4 nemaju cjelobrojnih rješenja, dok je x = 0 jedino cjelobrojno
rješenje jednadžbe x3 + x = 0.
To znači da je
{0, 1, -1, 2, -2}. Lako se vidi da jednadžbe
x3 + x = 1 i x3 + x
= 4 nemaju cjelobrojnih rješenja, dok je x = 0 jedino cjelobrojno
rješenje jednadžbe x3 + x = 0.
To znači da je
E( )tors =
{
)tors =
{ , (0,0)}
, (0,0)}

 .
.
y2 = x3 + 17.
Pokažite da se točke P3, P4, P5, P6 i P7 mogu prikazati u obliku [m] P1 + [n] P2, m, n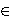

a) y2 = x3 + 4;
b) y2 = x3 + 8;
c) y2 = x3 - 4x;
d) y2 = x3 - 43x + 166.
| Web stranica seminara | Andrej Dujella - osobna stranica |