[Prethodna tema]
[Sljedeća tema]
3.2. Računanje ranga
Računanje ranga eliptičke krivulje nad
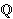 je vrlo težak problem i zapravo ne postoji algoritam
za računanje ranga proizvoljne eliptičke krivulje.
No, postoje metode pomoću kojih se u praksi često može
izračunati rang.
je vrlo težak problem i zapravo ne postoji algoritam
za računanje ranga proizvoljne eliptičke krivulje.
No, postoje metode pomoću kojih se u praksi često može
izračunati rang.
Pretpostavimo da E ima točku reda 2. U tom slučaju je
računanje ranga u pravilu lakše nego u općem slučaju.
Opisat ćemo metodu za računanje ranga koja se naziva
spust pomoću 2-izogenije.
Ako krivulja E dana jednadžbom
y2 = f(x) ima točku reda 2, onda
polinom f(x) ima racionalnu nultočku. Možemo
pretpostaviti da je ta racionalna nultočka upravo jednaka 0.
To znači da E ima jednadžbu oblika
y2 = x3 + ax2
+ bx.
Za krivulju E ' koja ima jednadžbu
y2 = x3 - 2ax2
+ (a2 - 4b)x
kažemo da je 2-izogena krivulji E.
Općenito, izogenijom zovemo homomorfizam između dvije
eliptičke krivulje koji je dan pomoću racionalnih funkcija. U našem
slučaju, radi se o preslikavanju
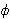 :
E(
:
E(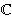 )
)
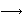 E '(
E '(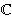 ),
),
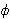 (x,y) =
(y2 / x2,
y(x2 - b) / x2).
(x,y) =
(y2 / x2,
y(x2 - b) / x2).
Zapišimo x i y u obliku x = m /
e2, y = n / e3,
te ih uvrstimo u jednadžbu od E. Dobivamo:
n2 = m(m2 +
ame2 + be4).
Stavimo b1 =
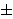 (m,b), gdje je
(m,b) najveći zajednički djelitelj od m i
b, s time da je predznak odabran tako da je
mb1 > 0. Tada je m =
b1m1, b =
b1b2, n =
b1n1, pa dobivamo
(m,b), gdje je
(m,b) najveći zajednički djelitelj od m i
b, s time da je predznak odabran tako da je
mb1 > 0. Tada je m =
b1m1, b =
b1b2, n =
b1n1, pa dobivamo
n12 = m1(b1m12 +
am1e2 +
b2e4).
Budući da je faktori na desnoj strani posljednje jednadžbe relativno
prosti, zaključujemo da postoje cijeli brojevi M i N
tako da vrijedi m1 = M2,
b1m12 +
am1e2 +
b2e4 = N2,
te tako konačno dobivamo jednadžbu
N2 = b1 M4
+ a M2 e2 +
b2 e4
(*)
u kojoj su nepoznanice M, e i N. Pritom
moraju biti ispunjeni sljedeći uvjeti:
(M,e) = (N,e) =
(b1,e) = (b2,M) =
(M,N) = 1.
Rang eliptičke krivulje E može se izračunati na sljedeći način.
Za svaku faktorizaciju b =
b1b2, gdje je b1
kvadratno slobodan broj, napišemo jednadžbu (*).
Pokušamo odrediti ima li ta jednadžba netrivijalnih cjelobrojnih
rješenja.
Svako rješenje (M, e, N) jednadžbe (*) inducira
točku na krivulji E s koordinatama x =
b1 M2 / e2,
y = b1 MN /
e3.
Neka je r1 broj faktorizacija za koje pripadna
jednadžba (*) ima rješenja, te neka je r2 broj
definiran na isti način za krivulju E '. Tada postoje
nenegativni cijeli brojevi e1 i e2
takvi da je r1 =
2e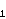 ,
r2 =
2e
,
r2 =
2e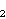 i pritom vrijedi da je
i pritom vrijedi da je
rank (E) = e1 + e2 - 2.
Primjer: Izračunajmo rang eliptičke krivulje
E : y2 = x3 - 5x.
Sada je pripadna 2-izogena krivulja
E ' :
y2 = x3 + 20x.
Za krivulju E, mogućnosti za broj b1 su
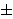 1,
1,
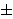 5.
Pripadne diofantske jednadžbe su
5.
Pripadne diofantske jednadžbe su
N2 = M4 -
5e4,
N2 = -M4 +
5e4,
N2 = 5M4 -
e4,
N2 = -5M4 +
e4.
Budući da je 12 = 34 -
5  24 i
22 = -14 + 5
24 i
22 = -14 + 5
 14,
zaključujemo da je r1 = 4 i e1 = 2.
14,
zaključujemo da je r1 = 4 i e1 = 2.
Za E' je b1'
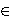 {
{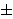 1,
1,
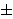 2,
2,
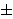 4,
4,
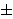 5,
5,
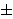 10,
10,
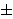 20}.
Međutim, b1' je kvadratno slobodan, a također je
očito da b1' i b2' ne mogu
oba biti negativni. To povlači da je
b1'
20}.
Međutim, b1' je kvadratno slobodan, a također je
očito da b1' i b2' ne mogu
oba biti negativni. To povlači da je
b1'
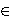 {1, 2, 5, 10}.
Očito je
12 = 14 +
20
{1, 2, 5, 10}.
Očito je
12 = 14 +
20  04 i
22 = 5
04 i
22 = 5  04 + 4.
Moramo odrediti ima li jednadžba
04 + 4.
Moramo odrediti ima li jednadžba
N2 = 2M4 +
10e4
rješenja. Budući da su M i N relativno prosti,
možemo pretpostaviti da je (M, 5) = 1. Tada je po
Malom Fermatovom teoremu M4
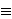 1 (mod 5) i N2
1 (mod 5) i N2
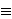 2 (mod 5). No, to je nemoguće jer kvadrati cijelih brojeva pri
djeljenju s 5 daju ostatke 0, 1, ili 4. Zaključujemo da je
r2 = 2, e = 1.
Konačno je rank (E) = 2 + 1 - 2 = 1.
2 (mod 5). No, to je nemoguće jer kvadrati cijelih brojeva pri
djeljenju s 5 daju ostatke 0, 1, ili 4. Zaključujemo da je
r2 = 2, e = 1.
Konačno je rank (E) = 2 + 1 - 2 = 1.
Uočimo da smo kod eliminiranja b1'-ova
za koje pripadna diofantska jednadžba nema rješenja
koristili činjenice da negativan broj ne može biti kvadrat
u 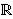 ,
te da broj 2 nije kvadrat u
,
te da broj 2 nije kvadrat u

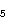 . No, kod diofantskih
jednadžbi stupnja većeg od 2 može se dogoditi da one imaju
rješenja u
. No, kod diofantskih
jednadžbi stupnja većeg od 2 može se dogoditi da one imaju
rješenja u 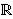 ,
te da imaju rješenja u
,
te da imaju rješenja u 
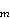 za svaki cijeli broj m, ali da ipak nemaju
netrivijalnih rješenja u
za svaki cijeli broj m, ali da ipak nemaju
netrivijalnih rješenja u  .
Jedan takav primjer je jednadžba
N2 = 17M4 -
4e4 koja se pojavljuje kod računanja ranga
eliptičke krivulje y2 = x3
+ 17x. U takvim slučajevima je određivanje ranga znatno teže.
.
Jedan takav primjer je jednadžba
N2 = 17M4 -
4e4 koja se pojavljuje kod računanja ranga
eliptičke krivulje y2 = x3
+ 17x. U takvim slučajevima je određivanje ranga znatno teže.
U slučaju krivulja bez 2-torzijskih točaka, osnovna ideja je
ponovo pridružiti krivulji E familiju krivulja
četvrtog stupnja. Metoda se naziva opći 2-spust i
puno je manje efikasna od spusta pomoću 2-izogenije.
No, i kad metode za direktno računanje ranga ne daju zadovoljavajući
rezultat, možemo pokušati pronaći što više nezavisnih točaka
na eliptičkoj krivulji, te tako odrediti barem donju ogradu za rang.
Recimo stoga nešto o tome kako se može provjeriti
nezavisnost točaka na eliptičkoj krivulji. To se radi tako da se
provjeri da jedna determinanta ne isčezava. Determinata o kojoj
je riječ je tzv. regulator
R = |det
(h'(Pi, Pj))|.
Ovdje je
h'(P, Q) = (h'(P + Q) -
h'(P) - h'(Q))/2,
dok je h'(P) kanonska visina točke P
definirana sa
h'(P) = lim h(2n P)
/ 4n,
gdje je h(P) naivna visina, tj. ako je
P = (x / z, y / u),
onda je h(P) = log max {|x|, |z|}.
Zadatci:
- Odredite rang sljedećih eliptičkih krivulja
a) y2 = x3 + x;
b) y2 = x3 - 4x;
c) y2 = x3 + 5x;
d) y2 = x3 + 14x;
e) y2 = x3 - 82x.
- Na krivulji
y2 = x3 - x2 - 3225667994796x
+ 2205916672708538820
nađite sve cjelobrojne točke P = (x,y)
takve da je |x| < 10000000.
Formulirajte neku hipotezu o rangu ove krivulje.
Provjerite svoju hipotezu koristeći neki od programa
za računanje ranga
(mwrank,
apecs,
simath)
[Prethodna tema]
[Sljedeća tema]
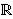 ,
te da broj 2 nije kvadrat u
,
te da broj 2 nije kvadrat u

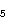 . No, kod diofantskih
jednadžbi stupnja većeg od 2 može se dogoditi da one imaju
rješenja u
. No, kod diofantskih
jednadžbi stupnja većeg od 2 može se dogoditi da one imaju
rješenja u 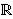 ,
te da imaju rješenja u
,
te da imaju rješenja u 
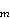 za svaki cijeli broj m, ali da ipak nemaju
netrivijalnih rješenja u
za svaki cijeli broj m, ali da ipak nemaju
netrivijalnih rješenja u  .
Jedan takav primjer je jednadžba
N2 = 17M4 -
4e4 koja se pojavljuje kod računanja ranga
eliptičke krivulje y2 = x3
+ 17x. U takvim slučajevima je određivanje ranga znatno teže.
.
Jedan takav primjer je jednadžba
N2 = 17M4 -
4e4 koja se pojavljuje kod računanja ranga
eliptičke krivulje y2 = x3
+ 17x. U takvim slučajevima je određivanje ranga znatno teže.
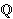 je vrlo težak problem i zapravo ne postoji algoritam
za računanje ranga proizvoljne eliptičke krivulje.
No, postoje metode pomoću kojih se u praksi često može
izračunati rang.
je vrlo težak problem i zapravo ne postoji algoritam
za računanje ranga proizvoljne eliptičke krivulje.
No, postoje metode pomoću kojih se u praksi često može
izračunati rang.
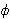 :
E(
:
E(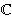 )
)
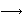 E '(
E '(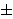 (m,b), gdje je
(m,b) najveći zajednički djelitelj od m i
b, s time da je predznak odabran tako da je
mb1 > 0. Tada je m =
b1m1, b =
b1b2, n =
b1n1, pa dobivamo
(m,b), gdje je
(m,b) najveći zajednički djelitelj od m i
b, s time da je predznak odabran tako da je
mb1 > 0. Tada je m =
b1m1, b =
b1b2, n =
b1n1, pa dobivamo
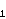 ,
r2 =
2e
,
r2 =
2e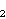 i pritom vrijedi da je
i pritom vrijedi da je
 24 i
22 = -14 + 5
24 i
22 = -14 + 5
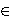 {
{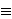 1 (mod 5) i N2
1 (mod 5) i N2