
 ,
,

 .
.

 ,
,

 .
.
Među poljima 
 ,
da bi se minimiziralo vrijeme potrebno za modularno
množenje, preporuča se da p ima oblik 2k
,
da bi se minimiziralo vrijeme potrebno za modularno
množenje, preporuča se da p ima oblik 2k
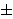 c
za neki mali prirodni broj c (npr. Mersenneovi
prosti brojevi oblika 2k - 1,
2160 + 7, 2255 + 95, i sl.).
c
za neki mali prirodni broj c (npr. Mersenneovi
prosti brojevi oblika 2k - 1,
2160 + 7, 2255 + 95, i sl.).
Kod polja karakteristike 2, osim broja elemenata, moramo odabrati i način reprezentacije elemenata. Najčešće se koriste trinomijalne i optimalne normalne baze. Kao što smo ranije napomenuli, izbor takvih baza omogućuje efikasniju implementaciju. No, takve baze ne postoje za svako konačno polje karakteristike 2, pa i to utječe na izbor polja. Neki popularni izbori su npr. 2163, 2191, 2239 i 2431.
Kod izbora eliptičke krivulje trebamo paziti da problem
diskretnog logaritma bude "težak". Kako smo već više puta
napomenuli, ECDLP je, prema svemu što vam je danas poznato,
vrlo težak problem. Međutim, postoje tipovi eliptičkih krivulja
kod kojih je taj problem nešto (ali čak puno) lakši.
Zato takve krivulje treba izbjegavati. Situacija je vrlo
slična kao kod kriptosustava koji svoju sigurnost
zasnivaju na teškoći faktorizacije velikih prirodnih brojeva
(npr. RSA ili Rabinov). I tamo je tvrdnja da je broj
oblika pq, gdje su p i q veliki prosti brojevi,
teško rastaviti na faktore
točna samo ako se p i q odaberu pažljivo
(npr. p i q ne smiju biti jako bliski;
brojevi p - 1 i q - 1 moraju imati barem jedan
veliki prosti faktor).
Navest ćemo sada tipove eliptičkih krivulja koje treba izbjegavati:

 )
nema niti jedan veliki prosti faktor. Preciznije,
#E(
)
nema niti jedan veliki prosti faktor. Preciznije,
#E(
 )
bi trebao imati barem jedan prosti faktor n veći od
2160, jer bi o protivnom protivnom ECDLP mogli
riješiti BSGS metodom. Obično se krivulja E odabire tako
da broj
#E(
)
bi trebao imati barem jedan prosti faktor n veći od
2160, jer bi o protivnom protivnom ECDLP mogli
riješiti BSGS metodom. Obično se krivulja E odabire tako
da broj
#E(
 )
oblika h
)
oblika h
 r,
gdje je r prost broj, a h = 1, 2 ili 4.
r,
gdje je r prost broj, a h = 1, 2 ili 4.

 ) = q.
Za takve krivulje postoji polinomijalni algoritam za ECDLP
koji su otkrili Smart,
Satoh, Araki i
Semaev. Stoga se analomalne
krivulje nikako ne bi smjele koristiti.
) = q.
Za takve krivulje postoji polinomijalni algoritam za ECDLP
koji su otkrili Smart,
Satoh, Araki i
Semaev. Stoga se analomalne
krivulje nikako ne bi smjele koristiti.

 ,
gdje je q = pk,
kažemo da je supersingularna ako p dijeli t.
Za krivulje nad
,
gdje je q = pk,
kažemo da je supersingularna ako p dijeli t.
Za krivulje nad

 za p
za p 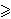 5
to znači da je t = 0, tj.
#E(
5
to znači da je t = 0, tj.
#E(
 ) = p + 1.
Za takve krivulje postoji tzv. MOV-napad
(Menezes, Okamoto,
Vanstone) koji u polinomijalnom vremenu
reducira ECDLP u polju
#E(
) = p + 1.
Za takve krivulje postoji tzv. MOV-napad
(Menezes, Okamoto,
Vanstone) koji u polinomijalnom vremenu
reducira ECDLP u polju
#E(
 )
na DLP u polju
)
na DLP u polju


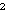 .
Zbog toga bi supersingularne krivulje trebalo izbjegavati.
Nadalje, trebalo bi izbjegavati sve krivulje za koje
postoji mali prirodni broj k (recimo k
.
Zbog toga bi supersingularne krivulje trebalo izbjegavati.
Nadalje, trebalo bi izbjegavati sve krivulje za koje
postoji mali prirodni broj k (recimo k
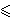 20)
takav da je qk
20)
takav da je qk
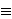 1
(mod #E(
1
(mod #E(
 )),
zato što u tom slučaju MOV-napad reducira ECDLP na DLP u polju
)),
zato što u tom slučaju MOV-napad reducira ECDLP na DLP u polju


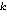 .
.

 ).
).
Primjer: Navest ćemo jedan primjer koji zadovoljava sve gore
navedene savjete i zahtjeve na izbor polja i eliptičke krivulje.
Neka je krivulja E zadana jednadžbom
y2 = x3 + x + 1010685925500572430206879608558642904226772615919
nad poljem E(
 ),
gdje je p = 2160 + 7.
Tada je
#E(
),
gdje je p = 2160 + 7.
Tada je
#E(
 ) =
1461501637330902918203683038630093524408650319587.
Može se dokazati (npr. metodom dokazivanja prostosti pomoću
eliptičkih krivulja!) da su brojevi p i
#E(
) =
1461501637330902918203683038630093524408650319587.
Može se dokazati (npr. metodom dokazivanja prostosti pomoću
eliptičkih krivulja!) da su brojevi p i
#E(
 )
prosti.
)
prosti.
 17.
17.
 23
sa svojstvom da je
#E(
23
sa svojstvom da je
#E( 23)
prost broj.
23)
prost broj.
| Web stranica seminara | Andrej Dujella - osobna stranica |