
 )
do točaka iz E(
)
do točaka iz E(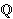 ).
).

 )
do točaka iz E(
)
do točaka iz E(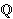 ).
).
Zbog toga možemo očekivati da ćemo kod kriptosustava zasnovanih na eliptičkim krivuljama postići zadovoljavajuću sigurnost s (puno) kraćim ključem nego kod kriptosustava zasnovanih na faktorizaciji ili običnom problemu diskretnog logaritma. Sada ćemo pokušati malo precizirati ovo razmatranje.
Pretpostavimo da imamo jedan kriptosutav zasnovan na DLP u
grupi 
 *,
te drugi zasnovan na ECDLP u grupi
E(
*,
te drugi zasnovan na ECDLP u grupi
E(
 ).
Ovdje su p i q prosti brojevi. Neka je M broj
bitova od p, a N broj bitova od q.
Brojeve M i N možemo interpretirati kao duljine
ključeva u pripadnim kriptosustavima. Stoga želimo naći odnos između
M i N, uz pretpostavku da su pripadni kriptosustavi
podjednako sigurni, tj. da su pripadni problemi diskretnog
logaritma podjednako teški.
).
Ovdje su p i q prosti brojevi. Neka je M broj
bitova od p, a N broj bitova od q.
Brojeve M i N možemo interpretirati kao duljine
ključeva u pripadnim kriptosustavima. Stoga želimo naći odnos između
M i N, uz pretpostavku da su pripadni kriptosustavi
podjednako sigurni, tj. da su pripadni problemi diskretnog
logaritma podjednako teški.
Najbolji poznati algoritmi za problem eliptičkog diskretnog logiritma
trebaju O(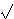 n)
operacija, gdje je n red grupe
E(
n)
operacija, gdje je n red grupe
E(
 *).
Kako je n vrlo blizu q, zaključujemo da je kompleksnost
promatranog ECDLP proporcionalna s 2N/2.
S druge strane, kompleksnog najboljeg poznatog algoritma za
problem običnog DLP je približno
*).
Kako je n vrlo blizu q, zaključujemo da je kompleksnost
promatranog ECDLP proporcionalna s 2N/2.
S druge strane, kompleksnog najboljeg poznatog algoritma za
problem običnog DLP je približno
exp(1.92 M1/3 (ln(M ln 2))2/3).
Primjetimo da je najbolji poznati algoritmi za faktorizaciju velikih brojeva imaju vrlo sličnu kompleksnost. Stoga će zaključci koje ćemo dobiti biti primjenjivi i na usporedbu kriptosustava zasnovanih eliptičkim krivuljama s onima zasnovanima na faktorizaciji (kao što je npr. RSA).Usporedbom gore navedenih kompleksnosti (zanemarujući konstante), dobivamo sljedeći odnos između M i N:
N 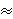 4.91 M1/3 (ln(M ln 2))2/3.
4.91 M1/3 (ln(M ln 2))2/3.
U članku iz 2001. godine, Lenstra i Verheul su dali preporuke za duljine ključeva koje bi trebalo koristiti da bi se postigla zadovoljavajuća sigurnost. Također su dali predviđanja o tome kako bi se te duljine ključeva trebale kretati u budućnosti. U svojim preporukama su uzeli u obzir više varijabilnih parametara. Jedan od osnovnih parametara uzima u obzir razumnu pretpostavku da najbolji javno objavljeni rezultati u razbijanju pojedinih kriptosustava ne predstavljaju garanciju da ne postoje i bolji (neobjavljeni) rezultati. Za parametar koji uzima ovu pretpostavku u obzir, uzeli su zadnju godinu u kojoj se smatra da je najpopularniji simetrični kriptosustav DES bio siguran. DES je kao standard prihvaćen 1976. godine. Kod njega je duljina ključa 56 bitova. Već tada je bilo mišljenja da je ta duljina ključa premala, međutim to javnog razbijanja DES-a došlo je tek 1997. godine. U podatcima u sljedećoj tablici koristi se pretpostavka da je zadnja godina u kojoj je DES bio siguran bila 1982. godina. Napomenimo da njihova predviđanja ne uzimaju u obzir moguću konstrukciju kvantnih računala, koja bi sve kriptostave javnog ključa koji su danas u uporabi učinila nesigurnima.
U tablici su dane preporučene duljine ključa u bitovima za simetrične kriptosustave (DES, AES), kriptosustave zasnovane na faktorizaciji ili diskretnom logaritmu u konačnom polju (RSA, ElGamal), te kriptosustave zasnovane na eliptičkim krivuljama. Uz to, dana je procjena kompjuterskog vremena potrebnog za razbijanje šifre u MIPS-godinama. Jedna MIPS (million-instructions-per-second) godina se definira kao količina računanja koje se može provesti u godinu dana na računalu sposobnom provesti milijun instrukcija u sekundi.
| Godina | DES duljina ključa | RSA duljina ključa | ECC duljina ključa | MIPS godina |
| 1990 | 63 | 622 | 117 | 3.51
 107
107 |
| 2000 | 70 | 952 | 132 | 7.13
 109
109 |
| 2010 | 78 | 1369 | 146 | 1.45
 1012
1012 |
| 2020 | 86 | 1881 | 161 | 2.94
 1014
1014 |
| 2030 | 93 | 2493 | 176 | 5.98
 1016
1016 |
| 2040 | 101 | 3214 | 191 | 1.22
 1019
1019 |
Možemo zaključiti da kriposustavi zasnovani na eliptičkim krivuljama, trenutno, uz 7 puta manju duljinu ključa pružaju istu sigurnost kao RSA kriptosustav, a u budućnosti se može očekivati da će taj omjer biti još povoljniji za ECC. To je osobito važno kod onih primjena (kao što su tzv. "pametne kartice") kod kojih je prostor za pohranu ključeva vrlo ograničen. Jasno je da su zbog toga eliptičke krivulje u posljednje vrijeme predmet velikog interesa kriptografa. Njihovim intenzivnijim proučavanjem može se očekivati da će otpasti i jedan od rijetkih argumenata protiv njihove uporabe u kriptografiji, a to je da su problemi na kojima je zasnovana uporaba eliptčkih krivulja u kriptografiji slabije istraženi, i puno kraće u žiži interesa kriptografa, od recimo problema faktorizacije.
No, u isto vrijeme interes za eliptičke krivulje raste i zbog njihove uloge u rješavanju važnih matematičkih problema, kao što je npr. Zadnji Fermatov teorem. Imajući u vidu sve navedeno, možemo očekivati da će i u godinama pred nama eliptičke krivulje predstavljati važan dio i čiste i primjenjene matematike.
| Web stranica seminara | Andrej Dujella - osobna stranica |