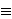 mi (mod pi).
Tada je m = mi
+ kpi), za neki cijeli broj k.
Tako dobivamo problem
mi (mod pi).
Tada je m = mi
+ kpi), za neki cijeli broj k.
Tako dobivamo problem
Opisat ćemo najprije Pohlig - Hellmanov algoritam redukcije kojim se određivanje broja m svodi na određivanje od m modulo svaki prosti faktor od n. Direktna posljedica postojanja ovog algoritma jest da ako želimo da kriptosustav zasnovan na ECDLP bude siguran, onda n mora imati veliki prosti faktor.
Pohlig - Hellmanov algoritam se može primijeniti u bilo kojoj abelovoj grupi G. Neka je red n od G djeljiv s prostim brojem p, te pretpostavimo da želimo riješiti problem diskretnog logaritma
Q = m P.
Problem se može reducirati na podgrupu od G reda p tako da se rješava problemQ' = n' Q = m0 (n' P) = m0 P',
gdje je n' = n / p i m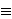 m0 (mod p). Stoga je P' točka reda
p. Rješenjem ovog novog problema određujemo vrijednost
m0, tj. određujemo m modulo p.
m0 (mod p). Stoga je P' točka reda
p. Rješenjem ovog novog problema određujemo vrijednost
m0, tj. određujemo m modulo p.
Vrijednosti od m modulo p2,
p3, ... , pc
(gdje je pc najveća potencija od p
koja dijeli n) određuju se na sljedeći način.
Pretpostavimo da je poznato da je m
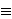 mi (mod pi).
Tada je m = mi
+ kpi), za neki cijeli broj k.
Tako dobivamo problem
mi (mod pi).
Tada je m = mi
+ kpi), za neki cijeli broj k.
Tako dobivamo problem
R = Q - mi P = k(pi P) = k S,
gdje su R i S poznati i S ima red s = n / pi. Vrijednost od k modulo p određuje se na isti način kao što je gore određena vrijednost od m modulo p.Nastavljajući ovaj postupak, rješavanjem problema diskretnog logaritma u podgrupama reda p, mi na kraju određujemo vrijednost m modulo pc. Nakon što izračunamo ovu vrijednost za sve proste djelitelje od m, sam broj m, tj. rješenje originalnog problema diskretnog logaritma, nalazimo primjenom Kineskog teorema o ostatcima.
Primjer: Neka je dana eliptička krivulja
E : y2 = x3 + 71x + 602
nad poljem 1009.
Red grupe E(
1009.
Red grupe E( 1009)
je 1060 = 22
1009)
je 1060 = 22  5
5  53.
Zadane su točke P = (1, 237), Q = (190, 271).
Treba riješiti problem eliptičkog diskretnog logaritma
Q = [m] P.
53.
Zadane su točke P = (1, 237), Q = (190, 271).
Treba riješiti problem eliptičkog diskretnog logaritma
Q = [m] P.
Točka P ima red 530 = 2  5
5  53
u grupi
53
u grupi  1009.
Dakle, kod nas je n = 530 i pomoću Pohlig-Hellmanovog
algoritma računanje broja m se reducira na računanje
od m modulo 2, 5 i 53.
1009.
Dakle, kod nas je n = 530 i pomoću Pohlig-Hellmanovog
algoritma računanje broja m se reducira na računanje
od m modulo 2, 5 i 53.
Modulo 2: Množeći točke P i Q s 530/2 = 265, dobivamo točke P2 = [265] P = (50, 0) i Q2 = [265] Q = (50, 0). Dobivamo problem
Q2 = (m mod 2) P2,
otkud očito slijedi da je m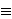 1 (mod 2).
1 (mod 2).
Modulo 5: Množeći točke P i Q s
530/5 = 106, dobivamo točke P5 = [106] P
= (639, 160) i Q5 = [106] Q = (639, 849).
Očito je Q5 = -P5,
što povlači m
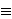 -1
-1
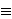 4 (mod 5).
4 (mod 5).
Modulo 53: Sada se točke množe s 530/53 = 10. Tako se dobivaju točke P53 = [10] P = (32, 737) i Q53 = [10] Q = (592, 97). Dobili smo problem diskretnog logaritma u grupi reda 53, koji ćemo riješiti malo kasnije kao ilustraciju BSGS metode.
Poznato je nekoliko metoda za rješavanje ECDLP koje imaju
kompleksnost
O(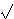 n).
Danas se najboljim smatra Pollardova
n).
Danas se najboljim smatra Pollardova
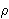 -metoda,
kod koje je za određivanje diskretmog logaritma potrebno
-metoda,
kod koje je za određivanje diskretmog logaritma potrebno
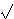 (
(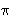 n)/2 zbrajanja
točaka na eliptičkoj krivulji. Mi ćemo ovdje opisati tzv.
baby step / giant step (BSGS) metodu čiji je autor
Daniel Shanks. Ova metoda je primjenjiva
na problem diskretnog logaritma u proizvoljnoj abelovoj grupi
G. Njezina kompleksnost je također
O(
n)/2 zbrajanja
točaka na eliptičkoj krivulji. Mi ćemo ovdje opisati tzv.
baby step / giant step (BSGS) metodu čiji je autor
Daniel Shanks. Ova metoda je primjenjiva
na problem diskretnog logaritma u proizvoljnoj abelovoj grupi
G. Njezina kompleksnost je također
O(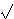 n),
gdje je n red grupe G, a pripadna konstanta je čak
i nešto bolja nego kod
n),
gdje je n red grupe G, a pripadna konstanta je čak
i nešto bolja nego kod 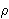 -metode. No, za razliku od
-metode. No, za razliku od
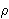 -metode,
BSGS metoda zahtjeva i pohranjivanje u memoriju
O(
-metode,
BSGS metoda zahtjeva i pohranjivanje u memoriju
O(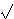 n)
elemenata grupe.
n)
elemenata grupe.
Slijedi opis BSGS metode. Neka su P, Q elementi grupe G, te neka je Q = m P. Po teoremu o dijeljenju s ostatkom, znamo da se m može zapisati u obliku
m = 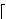
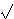 n
n![]](symbols/rceil.gif) a + b, gdje je 0
a + b, gdje je 0
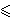 a, b <
a, b <
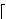
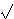 n
n![]](symbols/rceil.gif) .
.
(Q - b P) = a (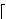
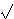 n
n![]](symbols/rceil.gif) P).
P).
Najprije izračunamo tablicu "baby stepova". Ta se tablica sastoji od svih vrijednosti
Rb = Q - b P,
za b = 0, 1, ... ,
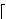
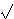 n
n![]](symbols/rceil.gif) - 1.
- 1.
Nakon toga računamo redom "giant stepove":
Sa = a (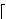
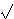 n
n![]](symbols/rceil.gif) P). ,
za a = 0, 1, ... ,
P). ,
za a = 0, 1, ... ,
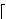
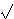 n
n![]](symbols/rceil.gif) - 1.
- 1.
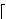
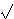 n
n![]](symbols/rceil.gif) .
.
Nastavak primjera: U gornjem primjeru, promatrali smo eliptičku krivulju
E : y2 = x3 + 71x + 602
nad 1009.
Nakon primjene Pohlig-Hellmanovog algoritma, originalni problem
smo sveli na određivanje broja m0 za kojeg vrijedi
Q' = [m0] P', gdje je
1009.
Nakon primjene Pohlig-Hellmanovog algoritma, originalni problem
smo sveli na određivanje broja m0 za kojeg vrijedi
Q' = [m0] P', gdje je
Q' = (592,97), P' = (32,737).
Znamo da je red od P' jednak 53. Kako je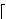
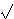 53
53![]](symbols/rceil.gif) = 8, trebamo napraviti osam "baby stepova". Dobivamo sljedeću
tablicu
= 8, trebamo napraviti osam "baby stepova". Dobivamo sljedeću
tablicu
| b | Rb = Q' - [b] P' |
| 0 | (592, 97) |
| 1 | (728, 450) |
| 2 | (537, 344) |
| 3 | (996, 154) |
| 4 | (817, 136) |
| 5 | (365, 715) |
| 6 | (627, 606) |
| 7 | (150, 413) |
Sada računamo "giant stepove":
| a | [a] ([8] P') |
| 1 | (996, 855) |
| 2 | (200, 652) |
| 3 | (378, 304) |
| 4 | (609, 357) |
| 5 | (304, 583) |
| 6 | (592, 97) |
Primjećujemo poklapanje za a = 6 i b = 0, što povlači m0 = 8a + b = 48. (Već iz a = 1 smo mogli zaključiti da je S1 = - R3, otkud je [8] P' = -Q + [3] P', što ponovo povlači da je m = -5 = 48 (mod 53).)
Vratimo li se sada na originalni problem Q = [m] P, za P = (1, 237), Q = (190, 271), dobivamo sustav kongruencija
m 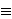 1 (mod 2),
m
1 (mod 2),
m 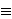 4 (mod 5),
m
4 (mod 5),
m 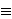 48 (mod 53),
48 (mod 53),
Napomenimo da za eliptičke krivulje specijalnih oblika postoje
i efikasniji algoritmi za ECDLP od gore navedenih.
Neke od tih algoritama ćemo spomenuti u idućem poglavlju.
Poznavanje tih algoritama je važno jer nam oni pokazuju
koje eliptičke krivulje trebamo izbjegavati u kriptografskim
primjenama.
 41*.
41*.
E : y2 = x3 + 71x + 602
nad poljem 1009 riješite problem diskretnog
logaritma Q = [m] P, gdje je
P = (32, 737), Q = (699, 888).
1009 riješite problem diskretnog
logaritma Q = [m] P, gdje je
P = (32, 737), Q = (699, 888).
| Web stranica seminara | Andrej Dujella - osobna stranica |