Declarations

So long as the value of lda is known, the following are valid:

    REAL, DIMENSION(100)       :: R
    REAL, DIMENSION(1:10,1:10) :: S
    REAL                       :: T(10,10)
    REAL, DIMENSION(-10:-1)    :: X
    INTEGER, PARAMETER :: lda = 5
    REAL, DIMENSION(0:lda-1)   :: Y
    REAL, DIMENSION(1+lda*lda,10) :: Z

The above example demonstrates:

• bounds can begin and end anywhere, (the array X),
• default lower bound is 1,
• there is a shorthand form of declaration, see T,
• arrays can be zero-sized. If lda were set to be zero,

      INTEGER, PARAMETER :: lda = 0

  then the array Y would be zero sized.

  Zero-sized arrays are useful when programming degenerate cases especially when invoking procedures (in this case we would expect lda to be a dummy argument which determines the size of some local (or automatic) array); no extra code has to be added to test for zero extents in any of the dimensions -- statements including references to zero sized arrays are simply ignored.

Now try this question

Return to corresponding overview page  

Consider the following declarations,

    REAL, DIMENSION(15)       :: A
    REAL, DIMENSION(-4:0,0:2) :: B
    REAL, DIMENSION(5,3)      :: C
    REAL, DIMENSION(0:4,0:2)  :: D

Individual array elements are denoted by subscripting the array name by an INTEGER, for example, A(7) element of A, or C(3,2), 3 elements down, 2 across.

The arrays can be visualised as below:

 
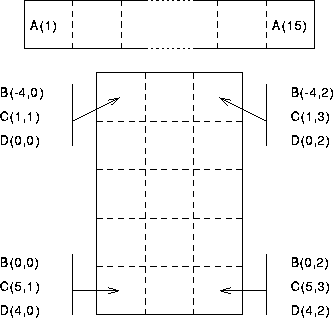
Figure 8: Visualisation of Arrays

The first dimension runs up and down the page and the second dimensions runs across the page.

Now try this question

Return to corresponding overview page