Consider,
DO i = 1, n
DO j = 1, m
x = A(j)
y = B(j)
C(i,j) = x+y
END DO
END DO
with a nested loop such as this, it is the inner loops that must be examined first. Inspection of the j loop reveals that if copies were made of x and y for each iteration the loop would be INDEPENDENT. In order to parallelise, the directive:
!HPF$ INDEPENDENT, NEW (x,y)
should prefix the inner loop.
Attention can now turn to the outermost loop. We could perform all the i iterations at the same time if there was a separate DO j loop for each iteration. Specifying j to be a NEW variable would do exactly this, viz:
!HPF$ INDEPENDENT, NEW (j)
DO i = 1, n
!HPF$ INDEPENDENT, NEW (x,y)
DO j = 1, m
x = A(j)
y = B(j)
C(i,j) = x+y
END DO
END DO
After the loop x, y and j will have an undetermined value so cannot be used before being assigned a new value. (In regular Fortran they could be.)
Looking at the outermost leaves of Figure 55 will illustrate what
can
be performed in parallel. It can be seen that all ![]() iterations can be performed independently. There is no interaction
between any iterations.
iterations can be performed independently. There is no interaction
between any iterations.
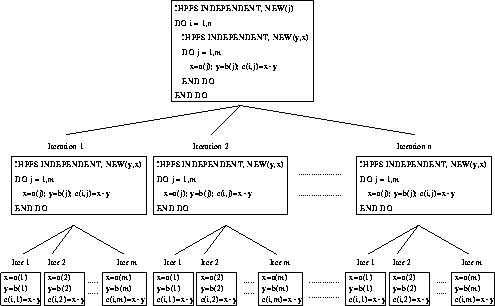
Figure 55: Visualisation of Double Nested Independent New Loop
Return to corresponding overview page ![]()