Nastava na daljinu

• Prezentacije za nastavu sukcesivno ću nadograđivati sa komentarima koje inače kažem na predavanju.
• Za svaki termin predavanja navest ću što je u planu napraviti od predavanja, a što od zadataka.
• Za izradu zadataka instalirajte si open source software Scilab ili Octave.
• Kada napravite zadatke, možete mi ih poslati mailom ili me pitati putem maila ukoliko imate bilo kakvih problema u implementaciji.
• U terminu predavanja, ponedjeljkom od 12.00 do 15.00 bit ću uz laptop i odgovarat ću promptno na vaša pitanja, tako da iskoristite to vrijeme za naš kolegij.

Obavijesti i zadaci uz konkretne termine

• 16.3.2020. - Iz prezentacije Sustavi linearnih jednadžbi: dovršite izradu zadataka za SOR metodu str. 67-73, proučite predavanja o Iteracijama iz Krylovljevih potprostora i o Metodi konjugiranih gradijenata str. 74-95., te izradite zadatak za Metodu najbržeg silaska str. 82-83.
  
  • Zadatak na str. 71, nakon unosa matrice A, vektora b i početnog vektora x0=zeros(4,1), rješavate na sljedeći način:
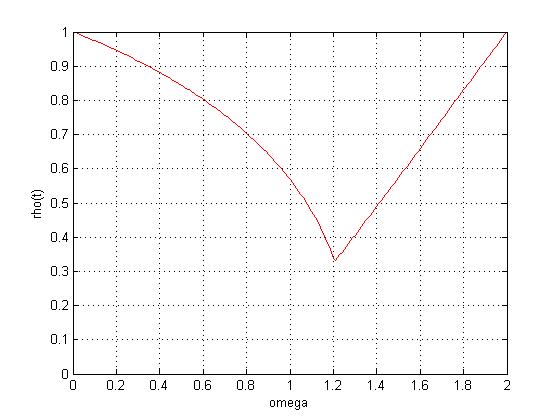
    >> sor_konvergencija(A)
>> [xgs,kgs,rgs]=sor(A,b,x0,1e-8,1) %za Gauss-Seidelovu metodu
>> [xsor,ksor,rsor]=sor(A,b,x0,1e-8,1.21) %za SOR metodu
>> semilogy(0:kgs,rgs,'r-',0:ksor,rsor,'g-')
>> xlabel('br. iteracija k')
>> ylabel('|| r_k ||/|| b|| ');
>> legend('Gauss-Seidel','SOR')
>> xlabel('br. iteracija k')
>> grid on
    Za Gauss-Seidelovu metodu dobije se aproksimacija rješenja u 28 iteracija, a za SOR metodu sa parametrom omega=1.21 17 iteracija. Egzaktno rješenje je x=[1 1 1 1]'. Grafovi su prikazani ispod.
    
    
    
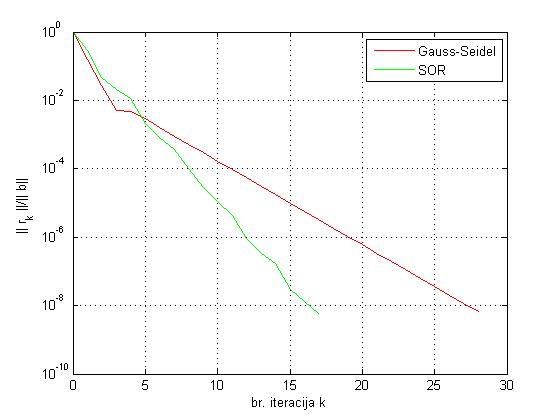
  • Zadatak na str. 72-73 rješava se na sličan način kao prethodne ali za dvije desne strane e i mu koji se zajedno sam matricom C nalazi u datoteci primjer_sustav_portfelj.m, pa ih iskopirajte od tamo. Optimalni parametar za SOR metodu je jako blizu 1, meni je ispao 1.01 pa nema velike razlike u odnosu na Gauss-Seidelovu metodu. Graf relativnih normi reziduala je ispod.
    
    
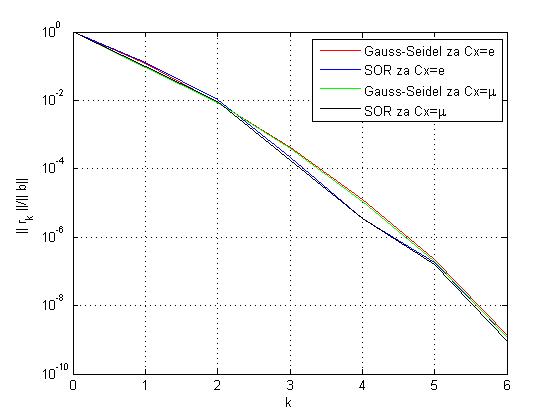
    Aproksimacije ješenja sustava SOR metodom ispadaju: xesor = %za sustav Cx=e

2.823984530396347
5.390070931236329
4.500322371250808

xmsor = %za sustav Cx=mu

0.250676982717219
0.117730496953165
0.244229529266018
    
    Težine portfelja sa najmanjom varijancom i sa očekivanim povratom mup=0.05 su
    omegamup =

0.255250404043139
0.382875606081094
0.361873989875767
    
    
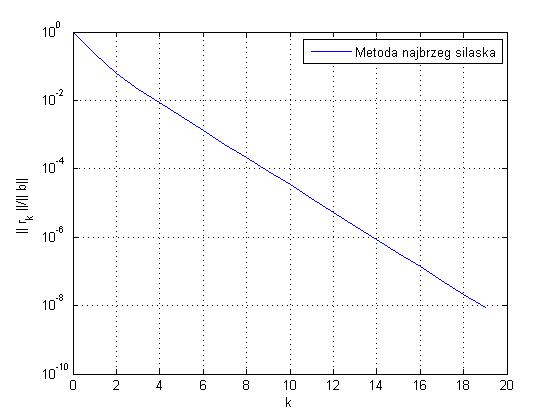
  • Zadatak na str. 83 daje aproksimaciju rješenja u 19 iteracija
    xns =

2.823984565133430
5.390070856851994
4.500322418015527
    
    Graf relativnih normi reziduala je ispod.
    
    
    
• 23.3.2020. - Iz prezentacije Sustavi linearnih jednadžbi: proučite predavanja o Metodi konjugiranih gradijenata str. 95-110., te izradite zadatke za Metodu konjugiranih gradijenata str. 103-110.
  - Iz prezentacije Problem svojstvenih vrijednosti: proučite uvodni Primjer str. 2-10, uvodne definicije i svojstva str. 11-14, te predavanja o Metodi potencija str. 15-25 i o Inverznim iteracijama str 26-31.
• 30.3.2020. - Iz prezentacije Problem svojstvenih vrijednosti: izradite zadatke za Metodu potencija i Inverznih iteracija str. 32-36, i proučite predavanja o Schurovoj dekompoziciji str. 37-68, i početak predavanja o Numeričkom računanju Schurove dekompozicije str. 69-84.
  • Zadatak na str. 32-33 dao je sljedeći rezultat:
    xk =

0.000028842621837
0.000220011986855
0.000595963053599
0.000451010517503
0.000232596587204
0.000204696356781
0.000033282270041
0.999999647535388
    
    Rayleighev koeficijent iznosi 1.000020857351191, broj iteracija potreban za postizanje zadane točnosti je 570, a kvocijent o kojem ovisi konvergencija iznosi 0.988177766265914 (što je blizu 1 pa je konvergencija spora). Graf normi reziduala je ispod.
    
    
    
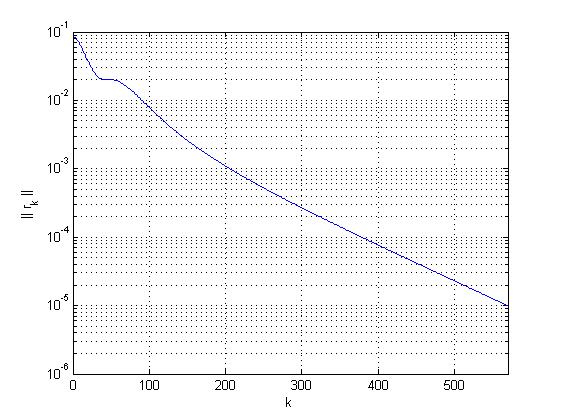
  • Zadatak na str. 34-36 dao je sljedeći rezultat:
    xk =

-0.000013521224454
-0.000094185757979
-0.000247756436143
-0.000185149040475
-0.000094737467292
-0.000082958874769
-0.000013470774431
-0.999999939621986
    
    Primijetite da je ovdje algoritam konvergirao prema vektoru [-1 0 0 0 0 0 0 0]', što je sasvim u redu jer zapravo tražimo jednodimenzionalni svojstveni potprostor i u njemu imamo dva moguća vektora norme 1. Rayleighev koeficijent iznosi 1.000008464483821, broj iteracija potreban za postizanje zadane točnosti je 3, a kvocijent o kojem ovisi konvergencija iznosi 0.077989531367031 (što je blizu 0 pa je konvergencija brza). Graf normi reziduala je ispod.
    
    
    
• 6.4.2020. - Iz prezentacije Problem svojstvenih vrijednosti: proučite predavanja o QR metodi str. 85-98. Izradite zadatke za svođenje matrice na Hessenebergov oblik str. 99 (pogledajte i podsjetnik na str. 100-102), i za QR metodu str. 103-108 (pogledajte i podsjetnik na str. 109-113). Počnite raditi zadatke za 1. Domaću zadaću str. 114-118. Proučite predavanja o Dekompoziciji singularnih vrijednosti str. 119-143 (radi se samo o kratkom opisu metode, samo da znate osnove, a detalji nisu važni).
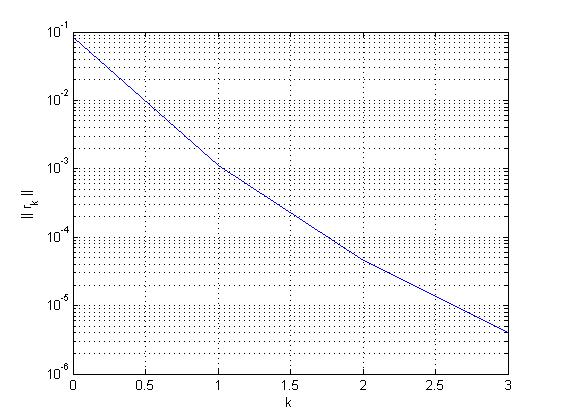
  • Zadatke iz ovog djela predavanja primijenite na računanju Schurove dekompozicije matrice za koju znate svojstvene vrijednosti, ili da ih izračunate pomoću funkcije eig(), ili je generirate kao A=X*D/X gdje je X neka slučajna matrica koja je gotovo uvijek regularna a D je dijagonalna matrica sa željenim svojstvenim vrijednostima.
  • Sa ovim predavanjima na red nam dolazi i prva domaća zadaća, molim da dobro pročitate upute i držite ih se kod izrade zadataka. Za predaju zadaće na e-mail ćete mi poslati
    • M-file funkcije sa svim traženim metodama i skripte koje provode testove na primjerima zajedno sa eventualnim .mat dadotekama koje sadrže ulazne i izlazne podatke (matrice neka budu minimalno dimenzije 10),
    • pismeni dio zadaće u obliku seminara koji sadrži sve što se traži, nemojte ispisivati same matrice nego navedite njihova bitna svojstva koja se traže,
    • svaka grupa svoje zadatke zajedno za oba partnera,
    • i to najkasnije do srijede 22.4.2020..
    Još jedna bitna stvar kod MATLAB programa koje ćete mi poslati je originalnost. Tolerirat ću samo da partneri iz grupe imaju slične ili iste kodove, ali svaka grupa mora imati jedinstvene programe. Međutim, svaki student mora imati svoje primjere, to znači da i partneri u grupi moraju imati različite primjere. Obzirom da ću imati sve vaše programe na jednom mjestu, vrlo lako ću to moći provjeriti. Isti programi u više od jedne grupe rezultirat će sa 0 bodova za sve partnere involviranih grupa, čime nećete ispuniti minimalne uvjete za ovaj kolegij. Osim toga, iz mog iskustva oni koji su prepisali zadatke i nisu se snalazili s njima, nisu bili u stanju riješiti praktični dio kolokvija. Zato vam preporučam da se potrudite oko ovih zadataka.
• 13.4.2020. - Iz prezentacije Problem najmanjih kvadrata: proučite uvodni Primjer str. 2-10, predavanja o Regresiji str. 11-14, Opis linearnog problema najmanjih kvadrata 15-25, predavanje o Numeričkom rješavanju problema najmanjih kvadrata str. 26-73, pri čemu
  • posebno obratite pažnju na Rješavanje problema najmanjih kvadrata pomoću QR faktorizacija str. 29-55, te izradite zadatak str. 56-57, rješenje tog zadatka je beta0=0.269449624506978 i beta1=0.799935398710618,
    • Dio ovog predavanja na str. 32-47 je samo podsjetnik, ali ga pogledajte, naročito dio o pivotiranju QR faktorizacije str. 39-41.
  • posebno obratite pažnju na Rješavanje problema najmanjih kvadrata pomoću dekompozicije singularnih vrijednosti str 58-71, te izradite zadatak str. 72-73, rješenje tog zadatka je beta0=0.269449624506978 i beta1=0.799935398710618, isto kao u prethodnom slučaju,
  te proučite predavanje o Problemu određivanja numeričkog ranga str. 74-78, i pogledajte zadatak na str. 78.
• 20.4.2020. - Iz prezentacije Problem najmanjih kvadrata: proučite primjer o Osjetljivosti numeričkog rješenja problema najmanjih kvadrata str. 79-84 i predavanja o Regularizaciji str. 85-93, o Krnjoj dekompoziciji singularnih vrijednosti (TSVD) str. 94-106, i o Generaliziranom problemu najmanjih kvadrata str. 107.
  - Iz prezentacije Interpolacija i aproksimacija splajnovima: proučite uvodni primjer str. 2-7, proučite predavanje o Interpolaciji po dijelovima polinomima str. 8-11, o Po dijelovima linearnoj interpolaciji str. 12-18, i Primjer str. 19-21, te izradite zadatak za Po dijelovima linearnoj interpolaciju str. 22-23. Napomena: Ova prezentacija bavi se po dijelovima polinomima, i sve ste to već čuli na kolegiju Numerička matematika. Zato se teorija bazira na ponavljanju gradiva sa tog kolegija, a mi ćemo se sad samo pozabaviti sa konkretnom implementacijom navedenih algoritama, i njihovom primjenom na probleme iz financijske matematike.
  • Zadatak na str. 22-23 daje sljedeći rezultat sa traženim grafom ispod.
    
    
    
• 27.4.2020. - Iz prezentacije Interpolacija i aproksimacija splajnovima: proučite predavanja o Po dijelovima kvadratnoj interpolaciji str. 24, o Po dijelovima kubičnoj interpolaciji str. 25-34, o Po dijelovima kubičnoj Hermiteovoj interpolaciji str. 35-39 i o Kubičnoj splajn interpolaciji str. 40-52, te izradite zadatke za Prirodni kubični splajn str. 53-60. Zatim proučite predavanja o Po dijelovima polinomnoj aproksimaciji pomoću diskretne metode najmanjih kvadrata str. 61-65, i o Po dijelovima linearnoj aproksimaciji pomoću diskretne metode najmanjih kvadrata str. 66-70, te izradite zadatke za Po dijelovima linearnu aproksimaciju pomoću diskretne metode najmanjih kvadrata str. 71-75.
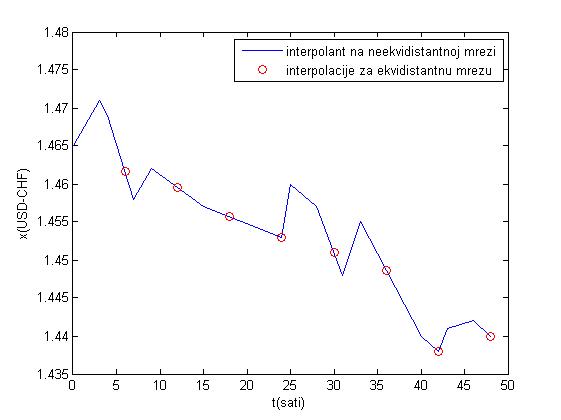
  • Zadatak na str. 71-75 daje sljedeći rezultat:

    alpha1 =

    0.2486 0.3733 0.4180 0.3700 0.6175 0.7381 0.9114 0.6742 0.9860 0.3323 1.1849

    alpha2 =

    0.2486 0.3733 0.4180 0.3704 0.6166 0.7448 0.8635 0.7546 1.0549

    alpha3 =

    0.3123 0.2291 0.3849 0.4432 0.5242 0.2969 0.4240 0.4229 0.4514 0.6888 0.5463 0.7163 0.6557 0.7915 0.6859 0.8973 0.7508 0.9640 0.7809 1.0490

    sa traženim grafovima ispod.
    
    
    
• 4.5.2020. - Iz prezentacije Interpolacija i aproksimacija splajnovima: proučite predavanja o Po dijelovima polinomnoj aproksimaciji pomoću neprekidne metode najmanjih kvadrata str. 76-85, i o Po dijelovima linearnoj aproksimaciji pomoću neprekidne metode najmanjih kvadrata str. 86-91, te izradite zadatke za Po dijelovima linearnu aproksimaciju pomoću neprekidne metode najmanjih kvadrata str. 92-95.
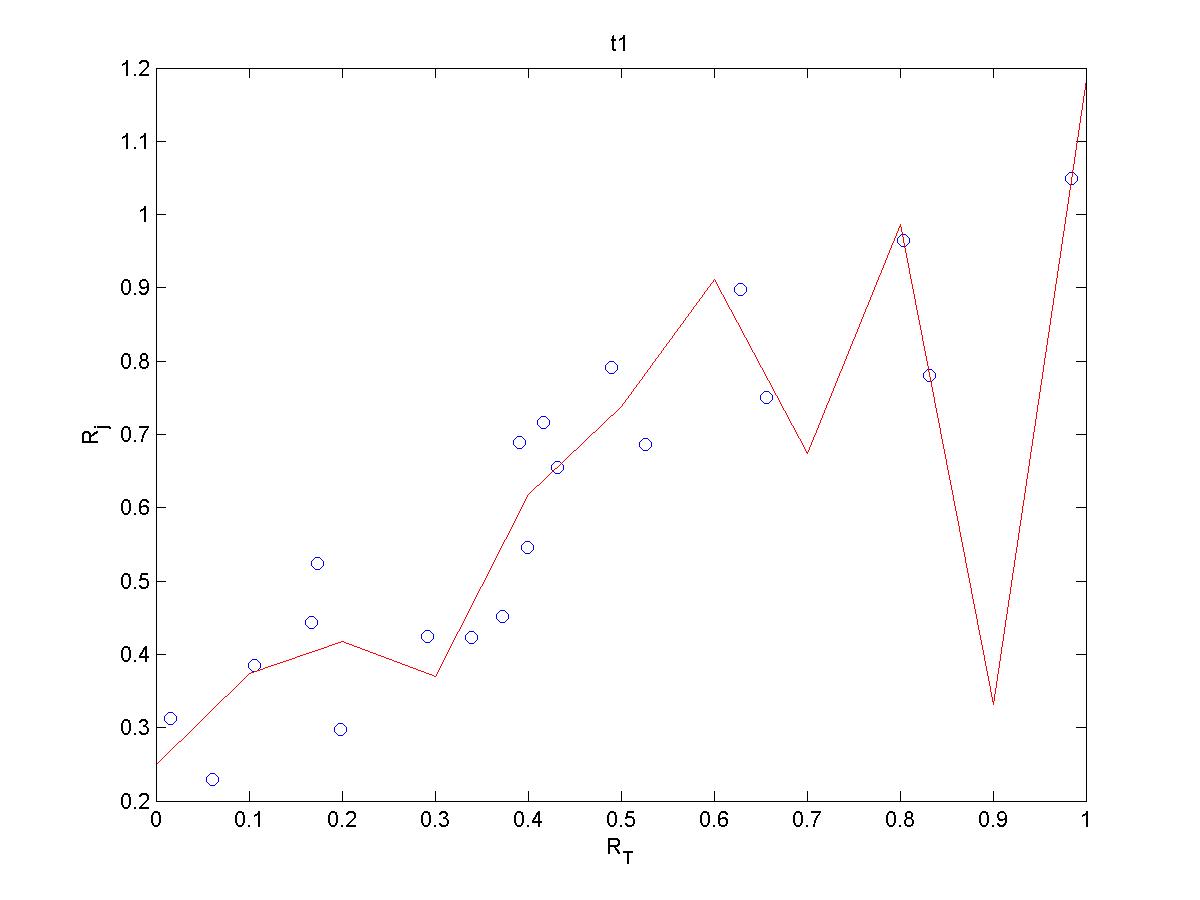
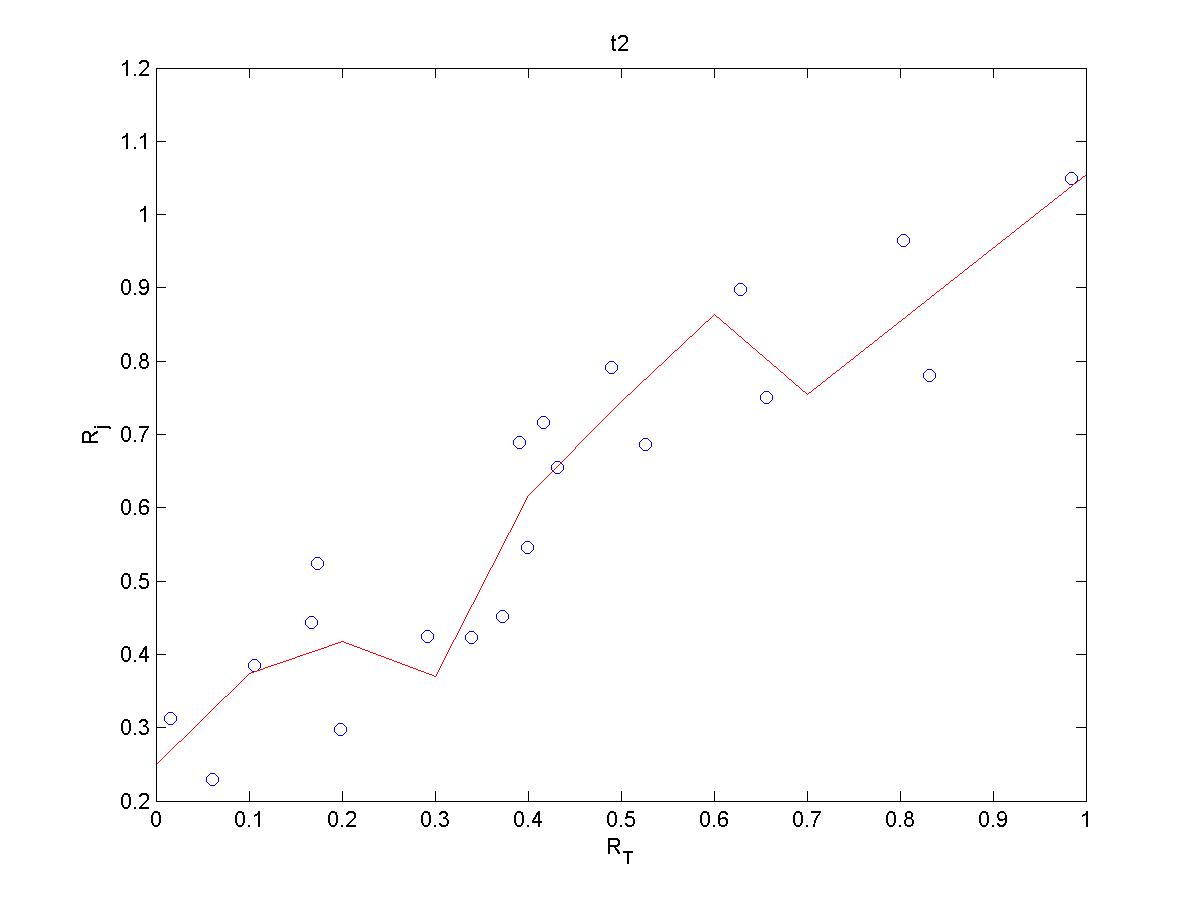
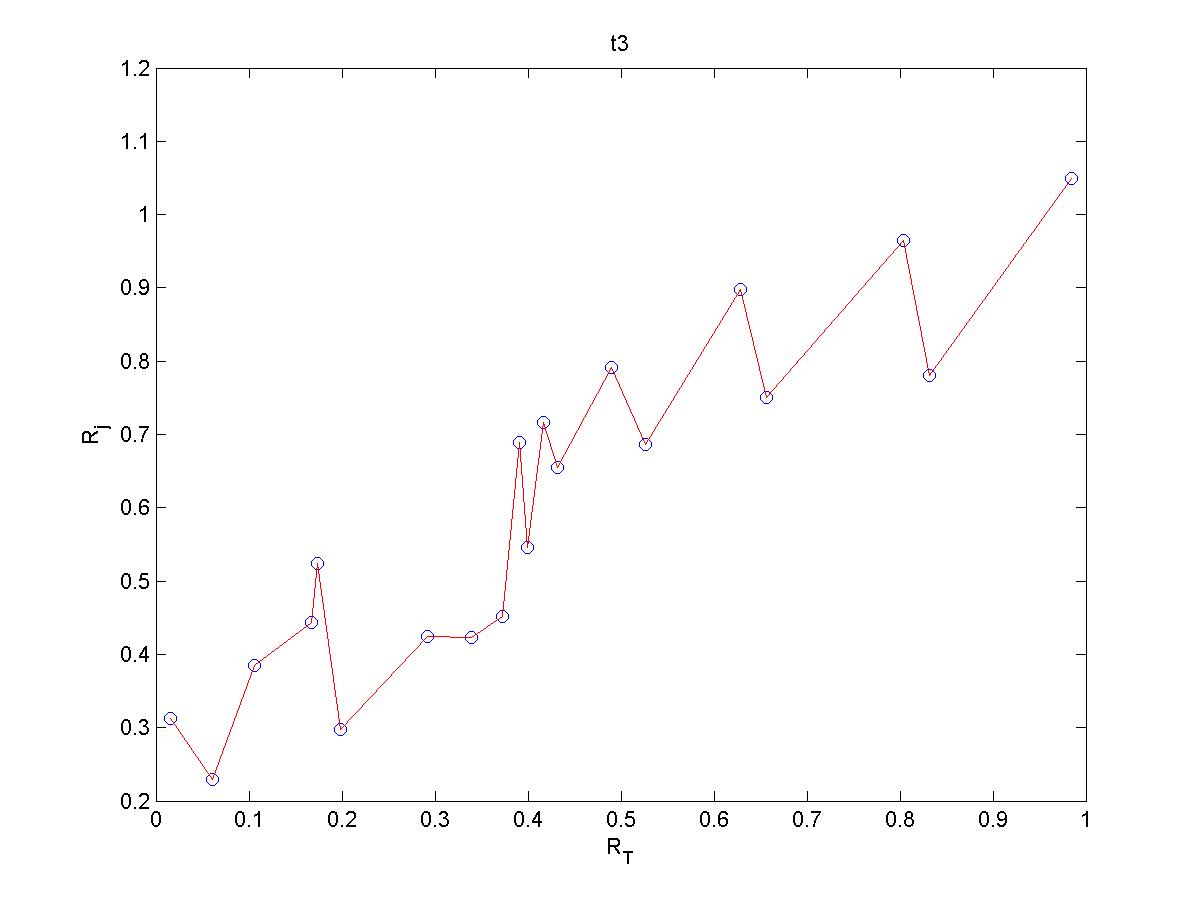
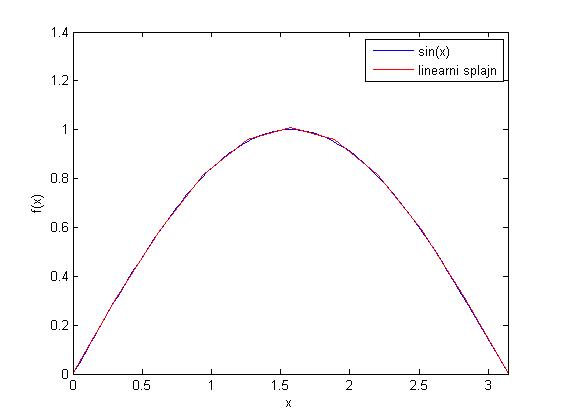
  • Zadatak na str. 92-95 daje sljedeći rezultat za koeficijente:
    alpha = [ 0.0006 0.3114 0.5927 0.8157 0.9589 1.0082 0.9589 0.8157 0.5927 0.3114 0.0006 ]'
    sa grafom funkcije i njene aproksimacije ispod.
    
    
    
  - Iz prezentacije Diskretna Fourierova transformacija: proučite uvodni primjer str. 2-4, i predavanje o Trigonometrijskoj interpolaciji str. 5-37.
• 11.5.2020. - Iz prezentacije Diskretna Fourierova transformacija: proučite predavanje o Brzoj Fourierovoj transformaciji (FFT) str. 38-54, i izradite zadatke za FFT str. 55-60. Počnite raditi zadatke za 2. Domaću zadaću str. 61-63.
  • Zadatak na str. 59-60 daje koeficijente faznog polinoma
    beta = [ 0.3133, 0.1350 - 0.1692i, 0.0364 - 0.0918i, 0.0313 - 0.0504i, 0.0312 - 0.0326i, 0.0312 - 0.0215i, 0.0312 - 0.0133i, 0.0312 - 0.0063i, 0.0312, 0.0312 + 0.0063i, 0.0312 + 0.0133i, 0.0312 + 0.0215i, 0.0312 + 0.0326i, 0.0313 + 0.0504i, 0.0364 + 0.0918i, 0.1350 + 0.1692i ]
    i koeficijente trigonometrijskog polinoma
    A = [ 0.6267 0.2700 0.0728 0.0626 0.0625 0.0625 0.0625 0.0625 0.0625 ]
    B = [ 0 0.3384 0.1835 0.1009 0.0652 0.0430 0.0265 0.0127 ]
    te maksimalna greške faznog polinoma u interpolacijskim točkama iznosi e = 3.2789e-015. Graf funkcije i interpolacijskih točaka na faznom polinomu prikazan je ispod.
    
    
    
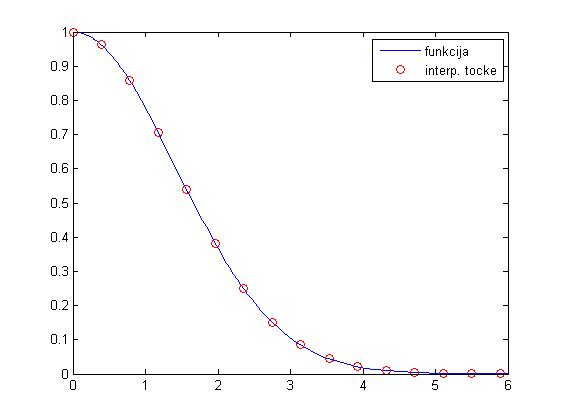
  • Sa ovim predavanjima na red nam dolazi i druga domaća zadaća, molim da dobro pročitate upute i držite ih se kod izrade zadataka. Za predaju zadaće na e-mail ćete mi poslati
    • M-file funkcije sa svim traženim metodama i skripte koje provode testove na primjerima zajedno sa eventualnim .mat dadotekama koje sadrže ulazne i izlazne podatke,
    • pismeni dio zadaće u obliku seminara koji sadrži sve što se traži,
    • svaka grupa svoje zadatke zajedno za oba partnera,
    • i to najkasnije do srijede 27.5.2020..
    Preporuka za ovu zadaću je ista kao i za prvu.
  - Iz prezentacije Numeričko rješavanje diferencijalnih jednadžbi proučite uvodni primjer str. 2-12 i predavanja o Numeričkom rješavanju paraboličke parcijalne diferencijalne jednadžbe str. 13, o Metodi konačnih razlika str. 14-21, i o Eksplicitnoj metodi konačnih razlika str. 22-28, te izradite zadatak za rješavanje difuzijske jednadžbe eksplicitnom metodom konačnih razlika str. 29-31 i zadatak za rješavanje Black-Scholesove jednadžbe eksplicitnom metodom konačnih razlika str. 32-36.
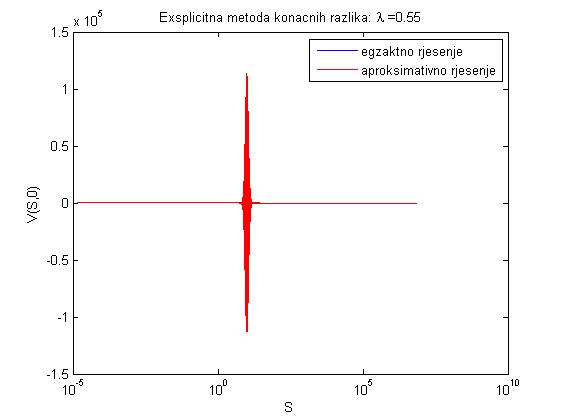
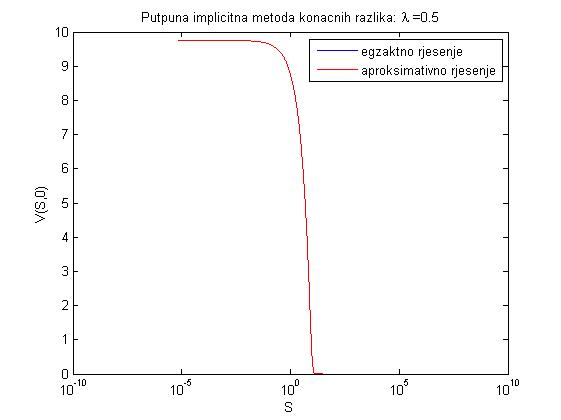
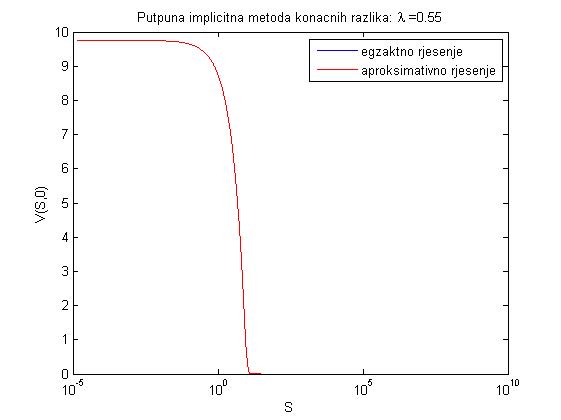
  • Zadatak na str. 29-31 daje grafove egzaktnog i aproksimativnog rješenja prikazanih ispod.
    
    
    
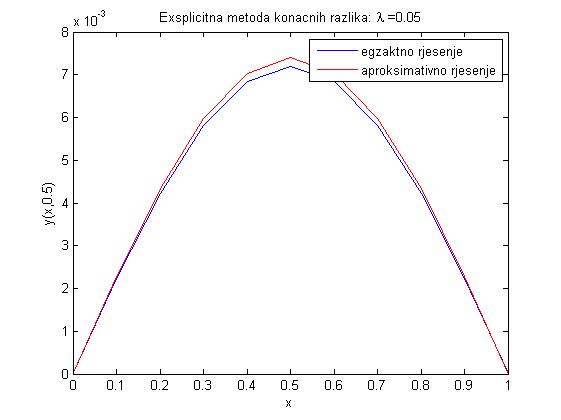
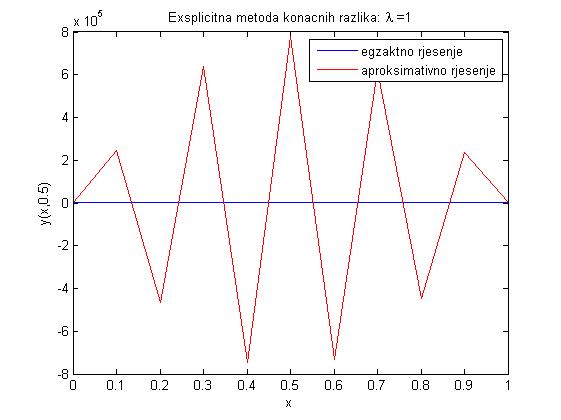
  • Zadatak na str. 32-36 daje sljedeće parametre, pri čemu maxe predstavlja maksimalnu grešku u čvorovima mreže, a kao egzaktno rješenje uzimamo ono što je vratila MATLAB-ova funkcija blsprice()
    • za lambda = 0.25: dtau = 1.0000e-004, dx = 0.0200, xmin = -20, xmax = 20, maxe = 7.3916e-004
    • za lambda = 0.5: dtau = 1.0000e-004, dx = 0.0141, xmin = -14.1421, xmax = 14.1421, maxe = 0.0015
    • za lambda = 0.55: dtau = 1.0000e-004, dx = 0.0135, xmin = -13.4840, xmax = 13.4840, maxe = 1.1339e+005
    Grafovi egzaktnog i aproksimativnog rješenja prikazani su ispod.
    
    
    
• 18.5.2020. - Iz prezentacije Numeričko rješavanje diferencijalnih jednadžbi proučite predavanja o Stabilnosti exsplicitne metode konačnih razlika str. 37-46, o Potpunoj implicitnoj metodi konačnih razlika str. 47-54, o Stabilnosti potpune implicitne metode konačnih razlika str. 55-59, izradite zadatak za rješavanje difuzijske jednadžbe potpunom implicitnom metodom konačnih razlika str. 60-63 i zadatak za rješavanje Black-Scholesove jednadžbe potpunom implicitnom metodom konačnih razlika str. 64-66, proučite predavanja o Crank–Nicolsonovoj metodi str. 68-77, o Stabilnosti Crank–Nicolsonove metode str. 78-84, te zadatak za rješavanje difuzijske jednadžbe Crank-Nicolsonovom metodom str. 85-88 i zadatak za rješavanje Black-Scholesove jednadžbe Crank-Nicolsonovom metodom str. 89-92.
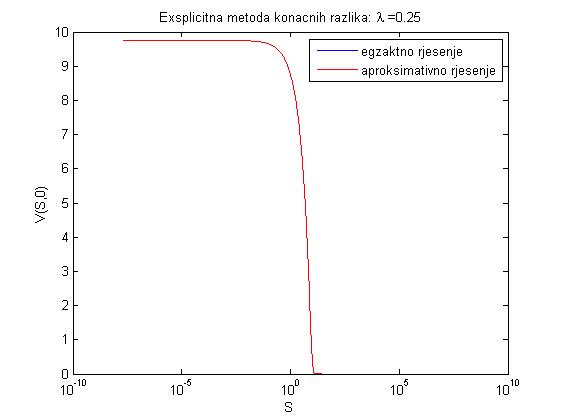
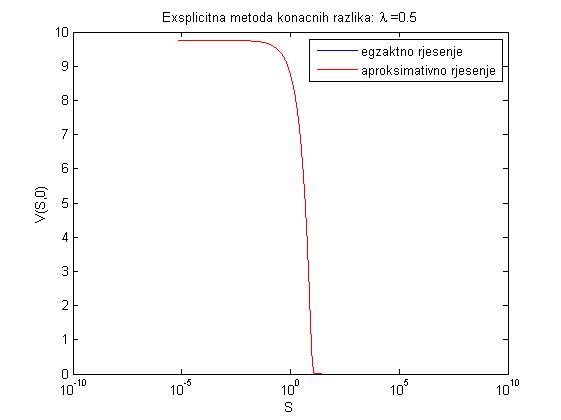
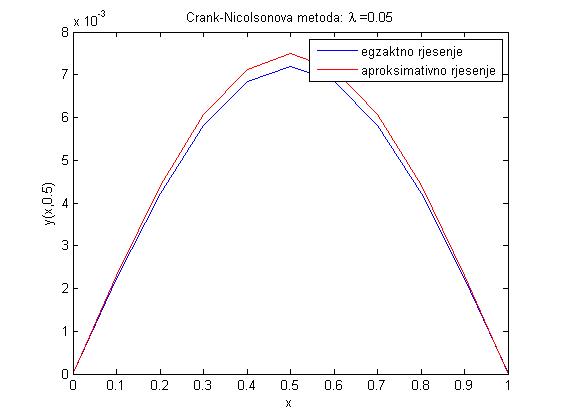
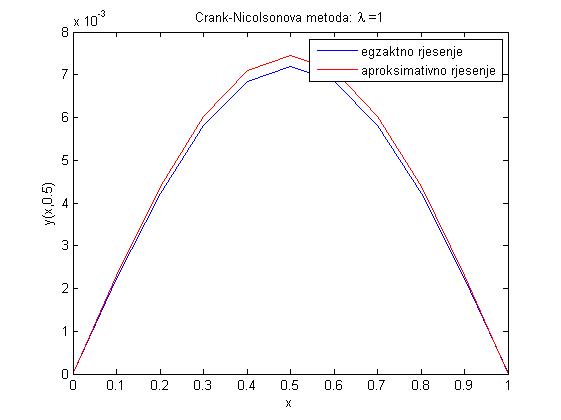
  • Zadatak na str. 60-63 daje grafove egzaktnog i aproksimativnog rješenja prikazanih ispod.
    
    
    
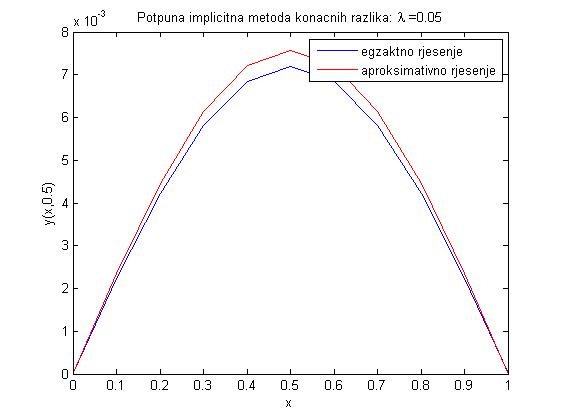
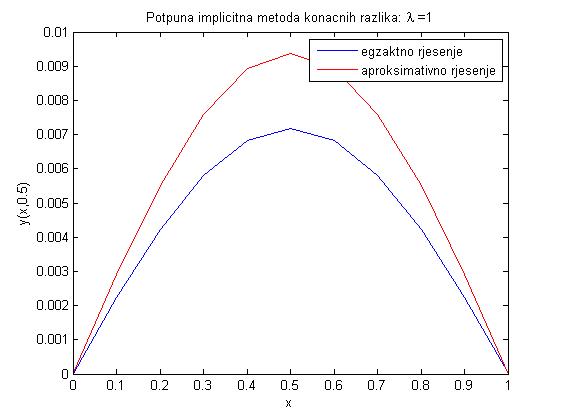
  • Zadatak na str. 64-66 daje sljedeće parametre, pri čemu maxe predstavlja maksimalnu grešku u čvorovima mreže, a kao egzaktno rješenje uzimamo ono što je vratila MATLAB-ova funkcija blsprice()
    • za lambda = 0.25: dtau = 1.0000e-004, dx = 0.0200, xmin = -20, xmax = 20, maxe = 0.0020
    • za lambda = 0.5: dtau = 1.0000e-004, dx = 0.0141, xmin = -14.1421, xmax = 14.1421, maxe = 0.0013
    • za lambda = 0.55: dtau = 1.0000e-004, dx = 0.0135, xmin = -13.4840, xmax = 13.4840, maxe = 0.0012
    Grafovi egzaktnog i aproksimativnog rješenja prikazani su ispod.
    
    
    
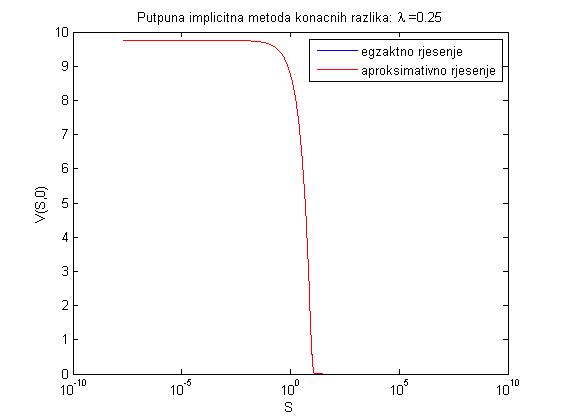
  • Zadatak na str. 85-8 daje grafove egzaktnog i aproksimativnog rješenja prikazanih ispod.
    
    
    
  • Zadatak na str. 89-92 daje sljedeće parametre, pri čemu maxe predstavlja maksimalnu grešku u čvorovima mreže, a kao egzaktno rješenje uzimamo ono što je vratila MATLAB-ova funkcija blsprice()
    • za lambda = 0.25: dtau = 1.0000e-004, dx = 0.0200, xmin = -20, xmax = 20, maxe = 0.0013
    • za lambda = 0.5: dtau = 1.0000e-004, dx = 0.0141, xmin = -14.1421, xmax = 14.1421, maxe = 6.6724e-004
    • za lambda = 0.55: dtau = 1.0000e-004, dx = 0.0135, xmin = -13.4840, xmax = 13.4840, maxe = 6.0637e-004
    Grafovi egzaktnog i aproksimativnog rješenja prikazani su ispod.
    
    
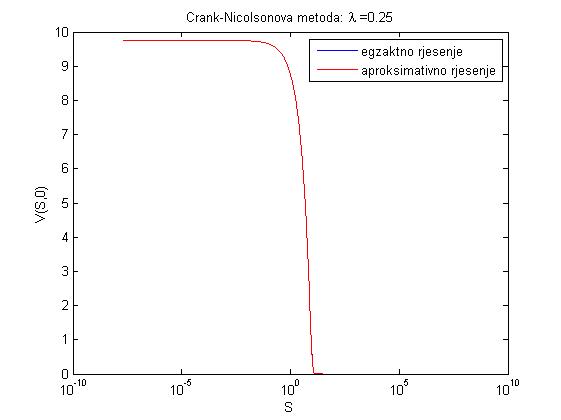
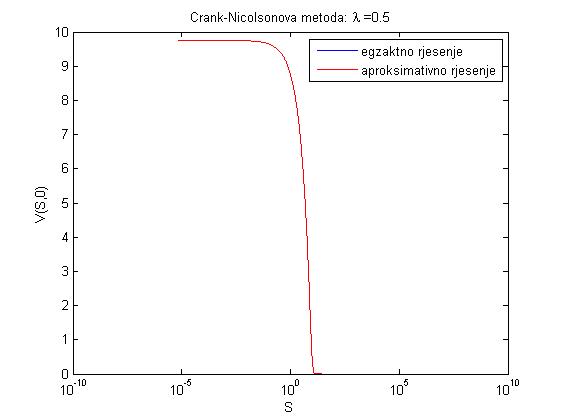
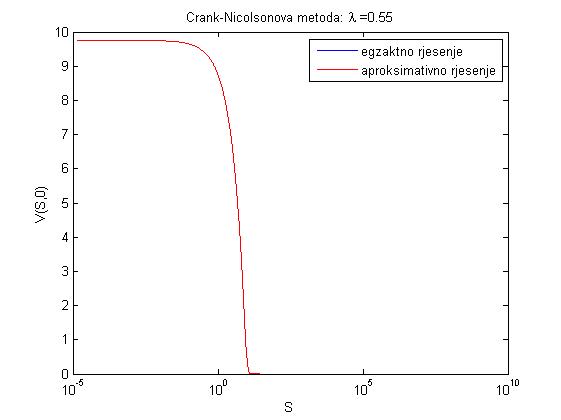
    Iz ovih primjera možemo primijetiti da je Crank-Nicolsonova metoda točnija od potpune implicitne metode konačnih razlika.

1. Točan odgovor je b) A1, jer ta matrica ma manje različitih svojstvenih vrijednosti.
2. Točne vrijednosti varijabli nosile su sljedeće bodove:
   • osor2 = 1
   • xe2 = 1
   • ke2 i re2 = 1
   • xmi2 = 1
   • kmi2 i rmi2 = 1
   • omega_minp2 = 2
3. Točne vrijednosti varijabli nosile su sljedeće bodove:
   • x3 = 2
   • k3 i r3 = 1
   • rk3 = 1
   • brzina_konvergencije3 = 1
4. Točne vrijednosti varijabli nosile su sljedeće bodove:
   • x4 = 3
   • r4 = 1
   • Sp4 = 1
5. Točne vrijednosti varijabli nosile su sljedeće bodove:
   • x5 = 0 (samo kontrola)
   • f5 = 1
   • s5 = 2
   • t5 = 0 (samo kontrola)
   • y5 = 2
6. Točne vrijednosti varijabli nosile su sljedeće bodove:
   • x6 = 0 (samo kontrola)
   • f6 = 1
   • beta6 = 2
   • A6 = 1
   • B6 = 1
7. Točne vrijednosti varijabli nosile su sljedeće bodove:
   • x7, nmin7 i nmax7 = 1
   • y7 = 3
   • m7 = 1
   • nmin7 = već uračunato sa x7
   • nmax7 = već uračunato sa x7
   • lambda7 = 1
   • Komentar točnosti aproksimacije rješenja = 1
8. Točne vrijednosti varijabli nosile su sljedeće bodove:
   • S8 = 1
   • V08 = 3

• Organizirajte se tako da mogu vidjeti što pišete na papir, možda da eventualno zalijepite nekoliko papira na zid, ili kako god vama odgovara samo da je vidljivo na kameri.