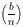 definira sa
definira sa
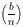 =
=
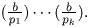 Ako je n prost, onda se Jacobijev i Legendreov simbol
podudaraju. Važno svojstvo Legendreovog simbola je
Eulerov kriterij:
Ako je n prost, onda se Jacobijev i Legendreov simbol
podudaraju. Važno svojstvo Legendreovog simbola je
Eulerov kriterij:
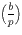 se definira ovako:
se definira ovako:
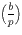 = 1 ako je b
kvadratni ostatak modulo p;
= 1 ako je b
kvadratni ostatak modulo p;
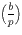 = -1 ako je b
kvadratni neostatak modulo p;
= -1 ako je b
kvadratni neostatak modulo p;
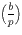 = 0 ako p dijeli
b.
= 0 ako p dijeli
b.
Neka je n neparan broj i n = p1
· · · pk njegov rastav na
(ne nužno različite) proste faktore.
Tada se Jacobijev simbol
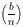 definira sa
definira sa
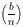 =
=
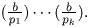 Ako je n prost, onda se Jacobijev i Legendreov simbol
podudaraju. Važno svojstvo Legendreovog simbola je
Eulerov kriterij:
Ako je n prost, onda se Jacobijev i Legendreov simbol
podudaraju. Važno svojstvo Legendreovog simbola je
Eulerov kriterij:
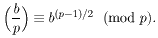
|
Definicija: Ako je n neparan složen broj, te b
cijeli broj takav da je (b,n) = 1 i vrijedi
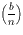 Jacobijev simbol, onda n zovemo
Eulerov pseudoprosti broj u bazi b (ili
epsp(b)).
Jacobijev simbol, onda n zovemo
Eulerov pseudoprosti broj u bazi b (ili
epsp(b)).
|
Kvadriranjem relacije (**) dobivamo bn -1 ≡ 1 (mod n), tj. relaciju (*). To znači da je svaki epsp(b) ujedno i psp(b). Međutim , obrat ove tvrdnje ne vrijedi.
Primjer 4.2: Vidjeli smo u Primjeru 4.1 da je 91 pseudoprost u bazi 3. Međutim,
345 ≡ 7297 . 27 ≡ 27 (mod 91),
pa 91 nije Eulerov pseudoprost broj u bazi 3. Ipak, 91 jest Eulerov pseudoprost u bazi 10 jer je1045 ≡ 100015 ≡ (-1)15 ≡ -1 (mod 91) i (10 / 91) = -1.
Pn = { b ∈
Zn* :
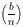 ≡
b(n -1)/2 (mod n) }.
≡
b(n -1)/2 (mod n) }.
| Teorem 4.2: Za sve neparne složene brojeve n vrijedi |Pn| ≤ φ(n)/2. |
Uočimo važnu razliku između Teorema 4.1.3) i 4.2. Naime, kod Eulerovih pseudoprostih brojeva nema analogona Carmichaelovih brojeva, već za svaki složen broj n, relacija (**) nije zadovoljena za barem pola mogućih baza.
Prije dokaza Teorema 4.2, dokažimo dvije leme. Koristit ćemo oznaku: νm(t) = najveći cijeli broj k takav da mk dijeli t.
Lema 4.1: Neka je n =
p1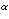  . . .
pr
. . .
pr  neparan broj,
te neka je
ν = min {
ν2
(pi-1) : i = 1, ... , r },
s = ∏i
(m, φ(pi neparan broj,
te neka je
ν = min {
ν2
(pi-1) : i = 1, ... , r },
s = ∏i
(m, φ(pi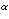 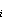 ).
Tada vrijedi: ).
Tada vrijedi:
(1) Kongruencija xm ≡ 1 (mod n) ima točno s rješenja. (2) Kongruencija xm ≡ -1 (mod n) ima rješenja ako i samo ako je ν2(m) < ν. (3) Ako kongruencija xm ≡ -1 (mod n) ima rješenja, onda ih ima točno s. |
Dokaz: Neka je gi primitivni korijen modulo
pi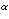
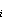 ,
tj. gia
≢
1 (mod pi
,
tj. gia
≢
1 (mod pi
 )
za a < φ(pi
)
za a < φ(pi
 ) =
pi
) =
pi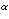
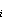 (1 - 1/pi ).
To znači da za svaki x
∈
{ 1, ... ,
pi
(1 - 1/pi ).
To znači da za svaki x
∈
{ 1, ... ,
pi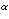
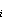 - 1 }
postoji j takav da je
gij
≡ x
(mod pi
- 1 }
postoji j takav da je
gij
≡ x
(mod pi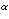
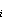 ).
Označimo taj j s
indi x.
Sada je kongruencija
xm
≡ c (mod n)
ekvivalentna sustavu kongruencija
).
Označimo taj j s
indi x.
Sada je kongruencija
xm
≡ c (mod n)
ekvivalentna sustavu kongruencija
m · indi x
≡
indi c (mod
φ(pi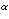
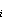 )),
za i = 1, ... , r.
(4.1)
)),
za i = 1, ... , r.
(4.1)
m · indi x
≡
0 (mod
φ(pi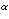
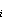 )),
za i = 1, ... , r.
)),
za i = 1, ... , r.
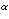
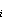 ))
rješenja. Stoga je ukupan broj rješenja sustava jednak s.
))
rješenja. Stoga je ukupan broj rješenja sustava jednak s.
Za c = -1 je indi (-1) =
φ(pi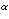
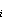 )/2,
pa sustav (4.1) postaje
)/2,
pa sustav (4.1) postaje
m . indi x
≡
φ(pi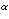
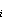 )/2 (mod
φ(pi
)/2 (mod
φ(pi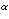
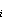 )),
za i = 1, ... , r.
)),
za i = 1, ... , r.
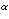
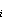 ))
dijeli φ(pi
))
dijeli φ(pi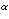
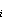 )/2.
Odavde imamo da
(2
)/2.
Odavde imamo da
(2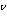 2(m) m1,
pi
2(m) m1,
pi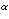 i -1 .
2
i -1 .
2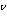 2(pi -1) q1) dijeli
pi
2(pi -1) q1) dijeli
pi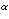 i -1 .
2
i -1 .
2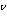 2(pi -1)-1 q1,
gdje su m1 i q1 neparni brojevi.
No, ovo je očito ekvivalentno s
ν2(m)
< ν2(pi-1) za
i = 1, ... , r, tj. s
ν2(m)
< ν.
2(pi -1)-1 q1,
gdje su m1 i q1 neparni brojevi.
No, ovo je očito ekvivalentno s
ν2(m)
< ν2(pi-1) za
i = 1, ... , r, tj. s
ν2(m)
< ν.
■
|
Lema 4.2: Neka je n neparan broj, te
p1, ..., pr
svi različiti prosti faktori od n. Tada je
|
Dokaz: Neka je
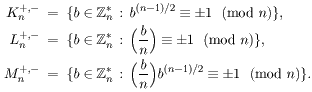
■
Dokaz Teorema 4.1: Neka je n =
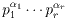 .
Iz Leme 4.2 slijedi
.
Iz Leme 4.2 slijedi
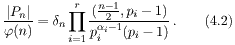
Sada možemo pretpostaviti da je αi = 1, tj. n = p1 · · · pr, r ≥ 2. Pretpostavimo da tvrdnja teorema ne vrijedi. Tada bi bilo Pn = Zn*. Neka je g primitivni korijen modulo p1 (ili bilo koji kvadratni neostatak modulo p1). Po Kineskom teoremu o ostatcima, možemo naći a ∈ Zn* takav da je a ≡ g (mod p1) i a ≡ 1 (mod n/p1). Budući da je Zn* = Pn, to je a(n-1)/2 ≡ (a/n) (mod n). Međutim, (a/n) = (a/p1) (a/(n/p1)) = (g/p1) = -1. Zato je a(n-1)/2 ≡ -1 (mod n/p1), što je u suprotnosti s a ≡ 1 (mod n/p1).
■
|
Korolar 4.1: Neka je
n ≡ 3
(mod 4) složen broj s r različitih prostih faktora. Tada je
|Pn| ≤ φ(n)/2r -1. |
Dokaz: Iz relacije (4.2) imamo:
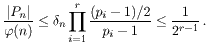
■
Solovay-Strassenov test je primjer tzv. Monte Carlo algoritma koji uvijek daje odgovor, ali on može biti netočan. Drugi tip vjerojatnosnog algoritma je Las Vegas algoritam koji ne daje uvijek odgovor, ali kada ga da, onda je odgovor sigurno točan. Primjer takvog algoritma smo vidjeli kod faktorizacije RSA modula n ako je poznat tajni eksponent d.
Napomena: Navest ćemo svojstva Jacobijevog simbola koja se
koriste u njegovom računanju:
(1) a ≡ b (mod n) ⇒ (a/n) = (b/n)
(2)
(-1/n) = (-1)(n -1)/2,
(2/n) = (-1)(n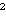 -1)/8
-1)/8
(3) (ab/n) = (a/n) (b/n)
(4) (m/n) = - (n/m) ako je m ≡ n ≡ 3 (mod 4), a (m/n) = (n/m) inače.
| Web stranica kolegija Kriptografija | Andrej Dujella - osobna stranica |