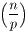[Prethodno poglavlje]   [Literatura]   [Sadržaj]

4.7. Metoda kvadratnog sita

Kvadratno sito je varijanta metode faktorske baze. Ovdje za faktorsku bazu B uzimamo

B = {p : p neparan prost broj, p ≤ P, 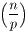(n/p) = 1} ∪ {2},

gdje je P broj odabran na neki optimalan način. Skup S u kojem tražimo B-brojeve (to su oni koji su djeljivi samo s prostim brojevima iz B bit će isti kao u Fermatovoj faktorizaciji, tj.

S = {t2 - n : ⌊√n⌋ + 1 ≤ t ≤ ⌊√n⌋ + A},

za neki prikladno odabrani A.

Glavna ideja ove metode je da umjesto da za svaki s ∈ S djeljeći ga s prostim brojevima p ∈ B provjeravamo da li je B-broj, mi uzimamo jedan po jedan p ∈ B i ispitujemo djeljivost sa p za sve s ∈ S. Odavde dolazi i naziv "sito", po analogiji s Eratostenovim sitom za generiranje tablice prostih brojeva. Opisat ćemo glavne korake u faktorizaciji neparnog složenog broja n metodom kvadratnog sita (QS), slijedeći [Koblitz: A Course in Number Theory and Cryptography, Poglavlje V.5].


Algoritam kvadratnog sita:

1. Odaberimo brojeve P i A, oba reda veličine exp(√(log n log log n)) = L(n). Obično se uzima da je P < A < P2. Funkcija L(n) ima red veličine između polinoma u log n i polinoma u n. Za n = 106 je L(n) ≈ 400; za n = 10200 je L(n) = 1023.

2. Za t = ⌊√n⌋ + 1, ⌊√n⌋ + 2, ... , ⌊√n⌋ + A, napravimo listu brojeva t2 - n (i stavimo ih u jedan stupac).

3. Za svaki prost broj p ≤ P, provjerimo da li je (n/p) = 1. Ako nije, izbacimo p iz faktorske baze.

4. Za neparan prost broj p takav da je (n/p) = 1, rješavamo kongruenciju t2 ≡ n (mod pβ) za β = 1, 2, ... . Neka je β najveći prirodan broj za kojeg postoji t, ⌊√n⌋ + 1 ≤ t ≤ ⌊√n⌋ + A takav da je t2 ≡ n (mod pβ). Neka su t1 i t2 dva rješenja od t2 ≡ n (mod pβ) takva da je t2 ≡ -t1 (mod pβ)   (t1 i t2 nisu nužno iz S).

5. Za p iz točke 4., pogledamo listu iz točke 2. U stupcu ispod p stavimo broj 1 kod svih vrijednosti od t2 - n kod kojih p|(t - t1); promijenimo 1 u 2 kod onih kod kojih p2|(t - t1); promijenimo 2 u 3 ako p3|(t - t1), itd. sve do pβ. Potom napravimo sve isto s t2 umjesto t1. Najveći broj koji će se pojaviti u ovom stupcu bit će β.

6. Svaki put kad u točki 5. stavimo broj 1 ili promijenimo 1 u 2, ili 2 u 3, ili itd., podijelimo odgovarajući t2 - n sa p i zabilježimo rezultat.

7. U stupcu ispod p = 2, ako n ≢ 1 (mod 8), onda stavimo broj 1 kod svih t2 - n u kojima je t neparan, te podijelimo t2 - n s 2. Ako je n ≡ 1 (mod 8), onda rješavamo kongruenciju t2 ≡ n (mod 2β) i radimo sve isto kao za neparne p (osim što će za β ≥ 3 biti 4 različita rješenja t1, t2, t3, t4 modulo 2β).

8. Kad završimo sa svim prostim brojevima p ≤ P, odbacimo sve t2 - n, osim onih koji su postali jednaki 1 nakon dijeljenja sa svim potencijama prostih brojeva p ≤ P. Dobit ćemo tako tablicu kao u Primjeru 4.5, u kojoj će stupac koji odgovara bi imati vrijednosti elemenata t2 - n iz S koji su B-brojevi, a ostali stupci će odgovarati vrijednostima p ∈ P za koje je (n/p) = 1.

9. Ostatak postupka je isti kao kod Fermatove faktorizacije.


Primjer 4.7: Neka je n = 1042387. Uzmimo P = 50 i A = 500. Ovdje je ⌊√n⌋ = 1020. Naša faktorska baza se sastoji od 8 prostih brojeva {2, 3, 11, 17, 19, 23, 43, 47}. Budući da je n ≢ 1 (mod 8), u stupcu pod p = 2 stavljamo 1 kod svih neparnih brojeva između 1021 i 1520.

Opisat ćemo detaljno formiranje stupca pod p = 3. Želimo naći rješenje t1 = t1,0 + t1,1 . 3 + t1,2 . 32 + ... + t1,β-1 . 3β-1 kongruencije t12 ≡ 1042387 (mod 3β), t1,j ∈ {0, 1, 2}. Možemo uzeti t1,0 =1. Modulo 9 imamo: (1 + 3t1,1)2 ≡ 7 (mod 9), odakle je t1,1 = 1. Modulo 27 imamo: (1 + 3 + 9t1,2)2 ≡ 25 (mod 27), odakle je t1,2 = 2. Nastavljajući ovaj postupak do 37, dobivamo t1 = (210211)3 = 589 mod 37. Budući da je 589 < 1021, a 37 - 589 = 1598 > 1520, zaključujemo da je β = 6 i možemo uzeti t1 = 589 ≡ 1318 (mod 36) i t2 = 36 - 589 = 140   (t2 ≡ 1112 (mod 35)).

Sada konstruiramo "sito" za p = 3. Krenuvši od 1318, skačemo za po 3 broja na dolje do 1021 i na gore do 1519, te svaki put stavimo broj 1 u stupac i podijelimo odgovarajući t2 - n sa 3. Tada napravimo sve isto sa skokovima po 9, 27, 81, 243 i 729 brojeva (u stvari, za 729 nemamo skokova, već samo promijenimo 5 u 6 kod 1318 i podijelimo 13182 - 1042387 još jednom sa 3). Nakon toga ponovimo sve krenuvši u skokove od 1112, umjesto 1318. Ovaj put se zaustavljamo kod skoka za 243 brojeva.
Nakon što ovaj postupak primijenimo na preostalih 6 brojeva u faktorskoj bazi, dobit ćemo tablicu 500 × 8 u kojoj retci odgovaraju t-ovima između 1021 i 1520. Izbacimo li sve retke za koje se t2 - n nije reducirao na 1, tj. zadržimo li samo one retke za koje je t2 - n B-broj, dobivamo sljedeću tablicu:
t   t2 - n   2 3 11 17 19 23 43 47
1021   54   1 3            
1027   12342   1 1 2 1        
1030   18513     2 2 1        
1061   83334   1 1   1 1   1  
1112   194157     5   1       1
1129   232254   1 3 1 1   1    
1148   275517     2 3     1    
1175   338238   1 2     1 1 1  
1217   438702   1 1 1 2   1    
1390   889713     2 2   1   1  
1520   1268013     1   1   2   1

Sada tražimo relacije modulo 2 između redaka u ovoj matrici. Jedan takav slučaj nalazimo u prva tri retka. Tako dobivamo

(1021 · 1027 · 1030)2 ≡ (2 · 33 · 112 · 17)2 (mod 1042387).

Nažalost, brojevi pod kvadratom na obje strane ove kongruencije su ≡ 111078 (mod 1042387), tako da ne dobivamo ništa korisno. Međutim, ako kombiniramo peti i zadnji redak, dobivamo

(1112 · 1520)2 ≡ (33 · 17 · 23 · 47)2 (mod 1042387),   tj.

6478532 ≡ 4961792 (mod 1042387),

odakle dobivamo netrivijalni faktor (647853 - 496179, 1042387) = 1487. (Drugi faktor je 701.)


Očekivani broj operacija metodom kvadratnog sita je

O(exp())

dakle, isto kao kod metode eliptičkih krivulja. Spomenimo da je 1996. godine metodom kvadratnog sita faktoriziran tzv. RSA-129. To je broj od 129 znamenaka koji je produkt dva prosta broja od 64 i 65 znamenaka.


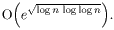
Trenutno najbolja poznata metoda faktorizacije je metoda sita polja brojeva (number field sieve) koja kombinira ideje iz metode kvadratnog sita i algebarsku teoriju brojeva. Kod ove metode je očekivani broj operacija

O(exp())

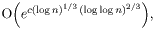
gdje je c = 3√(64/9) ≈ 1.92. Metodu je prvi put upotrijebio Pollard 1990. godine za faktorizaciju Fermatovog broja 229 + 1. Ovom su metodom faktorizirani brojevi iz natječaja RSA Factoring Challenge: RSA-130 (1996. godine), RSA-140, RSA-155 (oba 1999.), RSA-160, RSA-576 (oba 2003.), RSA-200, RSA-640 (oba 2005.). Npr. broj RSA-200 ima 200 znamenaka, dok broj RSA-640 ima 640 bitova (193 znamenke) (terminologija sa znamenaka na bitove je promijenjena 2001. godine). Brojevi su dizajnirani tako da slijede pravila za odabir modula u RSA algoritmu, te uspjesi u njihovoj faktorizaciji daju dobru informaciju o tome koliko velik RSA modul bi trebalo birati da bi nam komunikacija bila sigurna (danas, ali i u skoroj budućnosti). Broj RSA-640 je u studenom 2005. godine faktorizirala grupa njemačkih istraživača (Bahr, Boehm, Franke, Kleinjung). Evo tog broja i njegove faktorizacije:

3107418240490043721350750035888567930037346022842727545720161948823206440518081504556346829671723\
286782437916272838033415471073108501919548529007337724822783525742386454014691736602477652346609 =
1634733645809253848443133883865090859841783670033092312181110852389333100104508151212118167511579
× 1900871281664822113126851573935413975471896789968515493666638539088027103802104498957191261465571.

Broj RSA-240 (795 bitova) je u studenom 2019. faktorizirala grupa francuskih istraživača (Boudot, Gaudry, Guillevic, Heninger, Thomé, Zimmermann). Evo i tog broja i njegove faktorizacije:

124620366781718784065835044608106590434820374651678805754818788883289666801188210855036039570272508747509864768438458621\
054865537970253930571891217684318286362846948405301614416430468066875699415246993185704183030512549594371372159029236099 =
509435952285839914555051023580843714132648382024111473186660296521821206469746700620316443478873837606252372049619334517
× 244624208838318150567813139024002896653802092578931401452041221336558477095178155258218897735030590669041302045908071447.

[Prethodno poglavlje]   [Literatura]   [Sadržaj]
Web stranica kolegija Kriptografija Andrej Dujella - osobna stranica