3.4. Ostali kriptosustavi s javnim ključem

Neka je n = p . q, gdje su p i q prosti brojevi takvi da je p ≡ q ≡ 3 (mod 4). Neka je P = C = Zn i definiramo K = { (n, p, q) : n = pq }. Za K ∈ K definiramo eK(x) = x2 mod n, dK(y) = √y mod n. Vrijednost n je javna, a vrijednosti p i q su tajne.

Ovdje a = √b mod n znači da je a² ≡ b (mod n). Uvjet p ≡ q ≡ 3 (mod 4) se može izostaviti. No, uz ovaj uvjet je dešifriranje jednostavnije i efikasnije. Postoji i varijanta Rabinovog kriptosustava u kojoj se za šifriranje koristi općenitija kvadratna funkcija x(x + B), gdje je vrijednost B javna. Važno je uočiti da funkcija e_K nije injekcija. Naime, ako je w neki od 4 druga korijena iz 1 modulo n (dobiju se primjenom Kineskog teorema o ostatcima na kongruencije x ≡ ± 1 (mod p), x ≡ ± 1 (mod q), onda imamo:

e_K(wx) ≡ w² x² ≡ x² ≡ e_K(x) mod n.

Primjer 3.4: U Rabinovom kriptosustavu s parametrima

(n, p, q) = (437, 19, 23)

Najprije trebamo naći kvadratne korijene od 35 modulo 19 i modulo 23. Budući da je 19 ≡ 23 ≡ 3 (mod 4), možemo ih naći po formuli ± a^(p+1)/4 (mod p). Za p = 19, dobivamo 35⁵ ≡ 4 (mod 19), a za p = 23, 35⁶ ≡ 9 (mod 23). Sada koristimo Kineski teorem o ostacima da bi našli kvadratne korijene od 35 modulo 437 = 19 · 23, rješavajući 4 sustava linearnih kongruencija:

x ≡ ± 4 (mod 19),     x ≡ ± 9 (mod 23).

x ≡ a₁ (mod m₁),     x ≡ a₂ (mod m₂)

ElGamalov kriptosustav (Taher ElGamal, 1985) je zasnovan na teškoći računanja diskretnog logaritma u konačnim poljima.

Problem diskretnog logaritma: Neka je (G, *) konačna grupa, α ∈ G, H = { αi : i ≥ 0 } grupa generirana s α, te β ∈ H. Naći jedinstveni cijeli broj a takav da je 0 ≤ a ≤ |H| - 1 i αa = β, gdje je αa = α * α * ... * α (a puta). Taj cijeli broj a se zove diskretni logaritam i označava se s logα β.

U originalnom ElGamalovom kriptosustavu je (G, *) = (Z_p*, ·_p), dok je α primitivni korijen modulo p, tj. α ima svojstvo da je { αⁱ : i = 0, 1, ... , p - 1 } = Z_p*. To znači da je u ovom slučaju H = G. Najbolji poznati algoritmi za problem diskretnog logaritma u Z_p* trebaju

exp(O((log p)^1/3 (log log p)^2/3))

Definicija ElGamalovog kriptosustava:

Neka je p prost broj i α ∈ Zp* primitivni korijen modulo p. Neka je P = Zp*, C = Zp* × Zp* i K = { (p, α, a, β) : β ≡ αa (mod p) }. Vrijednosti p, α, i β su javne, a vrijednost a je tajna. Za K = (p, α, a, β) ∈ K i tajni slučajni broj k ∈ Zp -1 definiramo eK(x, k) = (y1, y2), gdje je y1 = αk mod p i y2 = x βk mod p. Za y1, y2 ∈ Zp* definiramo dK(y1, y2) = y2(y1a)-1 mod p.

Mogli bi reći da se otvoreni tekst x "zamaskira" množeći s β^k. Onaj tko poznaje tajni eksponent a može iz α^k izračunati β^k i "ukloniti masku".

Da bi eksponent a stvarno bio tajan, prost broj p mora biti dovoljno velik da bi u Z_p* problem diskretnog logaritma bio praktički nerješiv. Stoga se danas preporuča korištenje prostih brojeva od oko 1024 bita. Takoder bi red grupe, tj. broj p - 1, trebao imati barem jedan veliki prosti faktor (od barem 160 bitova).

Primjer 3.5: Neka je u ElGamalovom kriptosustavu p = 23, α = 5, a = 17, β = 15. Dešifrirati šifrat (y₁, y₂) = (17, 6).

Računamo y₁^a = 17¹⁷ ≡ 11 (mod 23). Potom nademo inverz od 11 modulo 23. Dobivamo da je inverz -2 ≡ 21 (mod 23). Konačno izračunamo 6 · 21 mod 23 i dobivamo otvoreni tekst x = 11.

Pored grupa Z_p*, u ovom kontekstu od interesa su i sljedeće grupe:

• multiplikativne grupe konačnih polja karakteristike 2:   GF(2ⁿ)
• grupe eliptičkih krivulja nad konačnim poljima:   EC(F)

ElGamalov kriptosustav u GF(2ⁿ)^* definira se na sasvim isti način kao u Z_p*. Naime, multiplikativna grupa svakog konačnog polja je ciklička. Najbolji poznati algoritmi za problem diskretnog logaritma u GF(2ⁿ) trebaju

exp(O(n^{1/4 + ε}))

Neka je p > 3 prost broj. Eliptička krivulja

E :       y² = x³ + ax + b

x₃ = m² - x₁ - x₂,       y₃ = m(x₁ - x₃) - y₁,

m = (y₂ - y₁) / (x₂ - x₁),   ako je P ≠ Q;
m = (3x₁² + a) / (2y₁),   ako je P = Q.

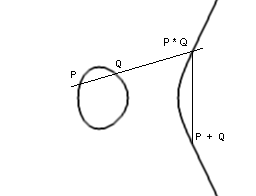
Geometrijski, zbrajanje možemo interpretirati tako da povučemo pravac kroz P i Q (ako je P = Q, onda povučemo tangentu). Taj pravac siječe E u tri točke: P, Q i recimo P * Q. Tada je P + Q osnosimetrična točka točki P * Q s obzirom na os x.

Kako je polovica elemenata iz Z_p* jednaka kvadratu nekog elementa iz Z_p*, za očekivati je da E ima približno p točaka (ako je točka (x, y) u E, onda je također i točka (x, -y) u E). Preciznije, po Hasseovom teoremu, vrijedi:

p + 1 - 2√p ≤ |E| ≤ p + 1 + 2√p.

Navest ćemo jednu varijantu ElGamalovog kriptosustava koja koristi eliptičke krivulje. Zove se Menezes - Vanstoneov kriptosustav. U njemu se eliptičke krivulje koriste samo za "maskiranje", dok su otvoreni tekstovi i šifrati proizvoljni uređeni parovi elemenata iz polja (a ne nužno parovi koji odgovaraju točkama na eliptičkoj krivulji). Kod ovog kriptosustava, šifrirana poruka je (samo) 2 puta dulja od originalne poruke, a ne 4 puta, koliko bi bila kod direktnog prevođenja ElGamalovog kriptusustava na grupu eliptičkih krivulja.

Neka je E eliptička krivulja nad Zp (p > 3 prost), te H ciklička podgrupa od E generirana s α. Neka je P = Zp* × Zp*, C = E × Zp* × Zp* i K = { (E, α, a, β) : β = aα }. Vrijednosti E, α, i β su javne, a vrijednost a je tajna. Za K = (E, α, a, β) ∈ K i tajni slučajni broj k ∈ Z|H|, te za x = (x1, x2) ∈ Zp* × Zp* definiramo eK(x, k) = (y0, y1, y2), gdje je y0 = kα, (c1, c2) = kβ, y1 = c1x1 mod p, y2 = c2x2 mod p. Za šifrat y = (y0, y1, y2) definiramo dK(y) = (y1(c1)-1 mod p, y2(c2)-1 mod p), gdje je ay0 = (c1, c2).

Najbolji poznati algoritmi za problem eliptičkog diskretnog logaritma trebaju O(√p) operacija. To pokazuje prednost kriptosustava zasnovanih na eliptičkim krivuljama u odnosu na RSA i ElGamalov kriptosustav. Naime, za postizanje iste sigurnosti kao kod RSA kriptosustava (a za ElGamalov vrijedi isto) s duljinom ključa od 1024 ili 4096 bita (a to su uobičajene vrijednosti), kod eliptičkih krivulja dovoljno je uzeti ključ duljine 160, odnosno 320 bitova. To je osobito važno kod onih primjena (kao što su npr. čip-kartice) kod kojih je prostor za pohranu ključeva vrlo ograničen.

Slično kao kod ElGamalovog kriptosustava, za primjene u kriptografiji, uz eliptičke krivulje nad poljima Z_p, važne su i krivulje nad poljima GF(2ⁿ). Napomenimo da ovdje (i općenito kod polja karakteristike 2), treba promatrati malo drugačiju jednadžbu, naime

E :       y² + xy = x³ + ax² + b.

Merkle-Hellmanov kriptosustav (Ralph Merkle i Martin Hellman, 1978) za osnovu ima tzv. problem ruksaka. Pretpostavimo da imamo n predmeta s volumenima v₁, v₂, ... , v_n koje želimo staviti u ruksak volumena V. Dakle, želimo naći podskup J ⊆ {1, 2, ... , n} tako da je ∑_j v_j = V, gdje suma ide po svim j ∈ J. Ekvivalentna formulacija je:

Za dani skup {v1, v2, ... , vn} od n prirodnih brojeva i prirodan broj V, naći niz m = (ε1, ε2, ... , εn) od n binarnih znamenaka (εi ∈ {0,1}) tako da je ε1v1 + ε2v2 + ... + εnvn = V, ako takav m postoji.

Poznato je da je ovaj opći problem ruksaka vrlo težak. On spada u tzv. NP-potpune probleme. To, pored ostalog, znači da nije poznat polinomijalni algoritam za njegovo rješavanje. Međutim, specijalni slučaj, tzv. superrastući problem ruksaka, je puno lakši. To je slučaj kad je niz v₁, v₂, ... , v_n rastući i vrijedi v_j > v₁ + ... + v_{j -1} za j = 2, 3, ... , n. Primjer superrastućeg niza je niz v_i = 2^{i -1}. Tada su ε_i-ovi upravo binarne znamenke broja V. Jasno je da u slučaju superrastućeg niza, u svakom koraku u ruksak moramo staviti najveći predmet koji u njega stane. Ova činjenica je osnova za Merkle-Hellmanov kriptosustav. Ideja Merkle-Hellmanovog kriptosustava je "zamaskirati" superrastući niz tako da izgleda kao sasvim slučajan niz. Onaj kome je poruka namjenjena zna kako ukloniti masku, pa može pročitati poruku rješavajući supperrastući problem ruksaka. Svi drugi moraju rješavati, puno teži, opći problem ruksaka, pa ne mogu pročitati poruku. "Maskiranje" se provodi modularnim množenjem.

Neka je v = (v1, v2, ... , vn) superrastući niz prirodnih brojeva, te neka je p > v1 + ... + vn prost broj i 1 ≤ a ≤ p - 1. Za 1 ≤ i ≤ n definiramo ti = a vi mod p i označimo t = (t1, ... , tn). Neka je P = {0,1}n, C = {0, 1, ... , n(p-1)} i K = {(v, p, a, t)}, gdje su v, p, a i t konstruirani na gore opisani način. Za K = (v, p, a, t) definiramo eK(x1, ... , xn) = x1t1 + x2t2 + ... + xntn. Za 0 ≤ y ≤ n(p-1) definiramo z = a-1y mod p, riješimo (superrastući) problem ruksaka za skup {v1, ... , vn, z} i tako dobivamo dK(y) = (x1, ... , xn). Vrijednost t je javna, dok su vrijednosti p, a i v tajne.

Primjer 3.6: Zadan je Merkle-Hellmanov kriptosustav s parametrima

v = (2, 5, 11, 23, 45, 91),   p = 181,   a = 111,   t = (41, 12, 135, 19, 108, 146).

Najprije izračunamo inverz od a modulo p (Euklidovim algoritmom). Dobivamo da je inverz 106. Zatim računamo z = 106 · 296 mod 181 = 63. Sada riješimo superrastući problem ruksaka za v i z. Dobivamo da je 63 = 45 + 11 + 5 + 2, pa je otvoreni tekst

(x₁, x₂, x₃, x₄, x₅, x₆) = (1, 1, 1, 0, 1, 0).

Merkle-Hellmanov kriptosustav je imao jednu vrlo veliku prednost u odnosu na ostale kriptosustave s javnim ključem. Naime, šifranje njime je znatno brže, te je on po brzini bio usporediv s najboljim simetričnim kriptosustavima. No, godine 1982. je uslijedilo razočaranje, kad je Adi Shamir pronašao polinomijalni algoritam za razbijanje Merkle-Hellmanovog kriptosustava. Pokazalo se da se ovako jednostavnim maskiranjem vrlo specijanog niza ipak ne dobiva sasvim slučajan niz. U razbijanju se koriste algoritmi za diofantske aproksimacije (verižni razlomci i LLL-algoritam). Prema tome, ovaj sustav se ne može više smatrati sigurnim kriptosustavom. Ipak, ideja na kojoj je zasnovan je vrlo zanimljiva. Ta ideja je korištenje u dešifriranju nekog jednostavnog specijalnog slučaja nekog teškog (NP-potpunog) problema, s time da se taj specijalni slučaj prikrije tako da izgleda kao opći.