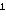
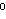 + 1 i
22
+ 1 i
22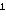
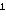 + 1.
+ 1.
Metode faktorizacije možemo podijeliti na opće i specijalne. Kod općih metoda očekivani broj operacija ovisi samo o veličini broja n, dok kod specijalnih ovisi također i o svojstvima faktora od n. Kod ocjene sigurnosti kriptosustava zasnovanih na faktorizaciji možemo se usredotočiti na opće metode.
Od specijalnih metoda spomenimo samo Pollardovu p-1 metodu iz 1974. godine. Neka je p prosti faktor od n.
Tada za svaki višekratnik m od p - 1 vrijedi
am ≡
1 (mod p). Pollardova p-1 metoda se sastoji u
računanju broja d = (am - 1, n).
Obično se uzima a = 2. Ako je 1 < d < n, onda smo
našli netrivijalni faktor od n.
No, pitanje je kako naći višekratnik od p-1 kad ne znamo p.
To možemo efikasno
napraviti u slučaju kada broj p-1 ima samo male proste faktore. Za prirodan broj
kažemo da je B-gladak ako su mu svi prosti faktori ≤ B. Pretpostavimo dodatno
da su sve potencije prostih brojeva, koje dijele p-1, manje ili jednake B. Tada
za m možemo uzeti najmanji zajednički višekratnik brojeva 1, 2, ... , B.
Za ovakav
m, broj operacija za računanje am - 1
mod n je ugrubo proporcionalan s B (preciznije
O(B log B (log n)2 +
(log n)3)). U najgorem slučaju, a to je kada je broj
Primjer 4.3: Neka je n = 540143.
Izaberimo B = 8 i
a = 2. Tada je m = 840. Imamo da je
2840 mod n = 53047 i (53046,n) = 421.
Zaista, n = 421 · 1283.
H. W. Lenstra je 1987. ideju Pollardove metode
primijenio na eliptičke krivulje. Naime, umjesto grupe
Zp* čiji je red p - 1, on je
koristio grupe E(Zp)
čiji redovi variraju između
exp(O((log n)1/2 (log log n)1/2))
(dakle, to je subeksponencijalni algoritam).
Spomenimo da su ovom metodom faktorizirani Fermatovi brojevi
22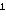
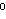 + 1 i
22
+ 1 i
22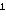
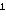 + 1.
+ 1.
| Web stranica kolegija Kriptografija | Andrej Dujella - osobna stranica |