Probability, Analysis, and Applications |
Workshop on the occasion of the 60th birthday of Professors Hrvoje Šikić and Zoran Vondraček
June 12-14, 2019
Abstracts |
Invited talks
|
Steven Bassnett (Washington University in St. Louis):
A stochastic engine controls eye growth To focus light sharply on the retina, the ocular lens must be a particular size and shape. Perhaps surprisingly, in view of the evident precision of eye growth, the underlying process appears to be stochastic. We show how a stochastic growth engine, operating within the unique geometry of the eye, is able to generate structures with the necessary precision. We also present recent work aimed at identifying the biological governors that regulate engine speed. |
|
Zhen-Qing Chen (University of Washington):
Jump diffusions and non-local operators In this talk, I will give a brief survey on heat kernel estimates for jump diffusions and non-local operators, including some recent progress on the stability of these estimates for pure jump Markov processes and for diffusions with jumps on metric measure spaces. |
|
Jakša Cvitanić (California Institute of Technology):
Large Tournament Games We consider a stochastic tournament game in which each player is rewarded based on her rank in terms of the completion time of her own task and is subject to cost of effort. When players are homogeneous and the rewards are purely rank dependent, the equilibrium has an explicit characterization, which allows us to conduct comparative statics and obtain explicit solution to several optimal reward design problems. In the general case when the players are heterogenous and payoffs are not purely rank dependent, we prove the existence, uniqueness and stability of the Nash equilibrium of the associated mean field game, and the existence of an approximate Nash equilibrium of the finite-player game. (Joint work with E. Bayraktar and Y. Zhang.) |
|
Joseph Glover (University of Florida):
Problems in Raw Time Changes of Markov Processes Let X(t) be a time-homogeneous Markov process, and let A(t) be a non-adapted (or raw) additive functional of X(t). Let T(t) be the right continuous inverse of A(t). In general T(t) is not a stopping time for each t. We will review conditions that assure X(T(t)) is once again a time-homogeneous Markov process and explore various open questions connected with this type of transformation. |
|
Eugenio Hernández (Universidad Autónoma de Madrid):
Extra invariance of PSI spaces and the Zak transfrom Let 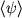 be the closure of the set of integer translations of be the closure of the set of integer translations of 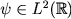 .
The space .
The space 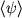 is clearly invariant under integer translations.
When is is clearly invariant under integer translations.
When is 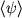 also invariant under translations by the elements of the group also invariant under translations by the elements of the group 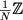 , , 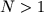 ?
We answer this question by giving a necessary and sufficient condition in terms of the Zak transform of ?
We answer this question by giving a necessary and sufficient condition in terms of the Zak transform of 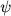 with respect to the group with respect to the group 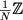 .
This result is extended to Principal Shift Invariant (PSI) spaces generated by a uniform lattice in a general locally compact abelian (LCA) group.
Joint work with D. Barbieri (Universidad Autónoma de Madrid) and C. Mosquera (Universidad de Buenos Aires). .
This result is extended to Principal Shift Invariant (PSI) spaces generated by a uniform lattice in a general locally compact abelian (LCA) group.
Joint work with D. Barbieri (Universidad Autónoma de Madrid) and C. Mosquera (Universidad de Buenos Aires).
|
|
Miljenko Huzak (University of Zagreb):
Approximate maximum likelihood estimation of drift parameters in a diffusion model A simple approximate maximum likelihood method of estimation of nonlinear drift parameters based on discrete observations of a diffusion path is analyzed asymptotically. In case of an ergodic diffusion and an equidistant sampling such that the maximal time of observation tends to infinity and size of time interval subdivision tends to zero in a way that their product tends to zero too, it is proved that approximate maximum likelihood estimator (AMLE) is consistent and asymptotically efficient and normally distributed. Moreover it turns out that under the same sampling the difference between AMLE and MLE based on continuous observation of the same path and over the same time interval goes to zero with rate equals to square root of time subdivision size. These properties can be used, for example, in proving asymptotic mixed normality of AMLE and hence for estimation of standard error of AMLE or for interval estimation of drift parameters that accounts effect of discretization. |
|
Moritz Kassmann (Universität Bielefeld):
Coercivity estimates for nonlocal quadratic forms We discuss the notions of ellipticity, non-degeneracy and coercivity for integro-differential operators generating Markov jump processes. We focus on operators generating nonlocal symmetric Dirichlet forms. In particular, implications of coercivity estimates for the corresponding regularity theory are explained. Throughout the talk we try to relate both probabilistic and analytic viewpoints on the subject. |
|
Panki Kim (Seoul National University):
Boundary potential theory for jump process: stable and beyond In this talk, we will take a journey on some boundary potential theories for jump processes. This talk is mainly based on 12 years joint works with Renming Song and Zoran Vondraček. |
|
Morten Nielsen (Aalborg University):
Muckenhoupt weights and shift invariant spaces Systems of translates of a single square integrable function are the basis of shift invariant subspaces and are used in the construction of wavelets and Gabor systems. In this talk we discuss some connections between stability of integer translates and certain Muckenhoupt conditions imposed on the corresponding periodization function. We are particularly interested in the borderline case where the system fails to form a Riesz basis, but still retains some stability. A factorisation of the periodization function related to the Garnett-Jones distance is used to identify some of the subclasses in this family. This is joint work with Hrvoje Šikić. |
|
Mihael Perman (University of Ljubljana):
Sampling excursions with some applications Brownian motion or, more generally, Markov processes can be decomposed into excursions. Labelling the excursions produces new and independent Poisson processes. This simple trick can be applied in many different situations. In the talk I will give several applications ranging from deriving the distribution of the Kolomogorov-Smirnov statistic, decompositions of Markov processes, Ray-Knight theorems and risk processes. |
|
Dražen Prelec (Massachusetts Institute of Technology):
Finding truth in a post-truth world The question whether to trust the judgments of a few experts or the wisdom-of-the-crowd is not just of scientific but also of political and philosophical interest. Crowd wisdom is usually defined as consensus — the majority vote or the median estimate or forecast. This principle seems fair and simple, but it has a blind spot for information that is new or unfamiliar. The cost of wrong collective decisions can be high in terms of environmental risks underestimated, or promising ideas ignored. The challenge is to combine the virtues of a 'democratic' procedure, which allows anyone, irrespective of credentials, to register an opinion, with an 'elitist' outcome that associates truth with the judgments of a select few. I will discuss alternatives to democratic averaging, based on asking crowd to 'self-reflect,' that is, asking people to predict how their peers will vote. |
|
Murali Rao (University of Florida):
On the notion of fractional derivative This note is one attempt to put the notion of fractional derivatives as a natural part of semigroup theory. R. Schilling, R. Song, and Z. Vondraček's book led the way for me. Many use the Riemann-Liouville integral for this. We use (as some others do) the Weyl transforms. These are actually in 'duality'. Using the Weyl integral one introduces another strongly continuous semigroup 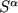 .
The Weyl integral is a fractional integral and naturally leads to fractional derivatives.
A Taylor's formula for the fractional integral .
The Weyl integral is a fractional integral and naturally leads to fractional derivatives.
A Taylor's formula for the fractional integral 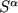 will also be derived.
There has been much work attempting to explaining memory using fractional integrals. None has gained universal acceptance.
In probability theory the exponential distribution is the only distribution without memory.
We will show that the exponential is the only survival function left invariant by will also be derived.
There has been much work attempting to explaining memory using fractional integrals. None has gained universal acceptance.
In probability theory the exponential distribution is the only distribution without memory.
We will show that the exponential is the only survival function left invariant by 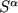 .
Simple examples will show that this subject is worth more study. .
Simple examples will show that this subject is worth more study.
|
|
Yan-Xia Ren (Peking University):
Stable Central Limit Theorems for Super Ornstein-Uhlenbeck Processes Let 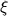 be an Ornstein-Uhlenbeck process on be an Ornstein-Uhlenbeck process on 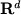 with generator with generator
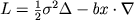 ,
where ,
where 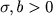 . Let . Let  be a branching mechanism which is close to a function of the form be a branching mechanism which is close to a function of the form
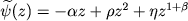 with with
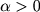 , , 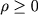 , , 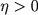 and and 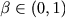 ,
in some sense.
We study asymptotic behaviors of ,
in some sense.
We study asymptotic behaviors of
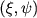 -superprocesses -superprocesses 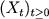 . For any testing function f of polynomial growth,
denote by . For any testing function f of polynomial growth,
denote by 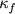 the order of f in the spectral decomposition of f in terms of the spectrum of the mean semigroup
of X.
Conditioned on non-extinction, we establish some stable central limit theorems for the order of f in the spectral decomposition of f in terms of the spectrum of the mean semigroup
of X.
Conditioned on non-extinction, we establish some stable central limit theorems for 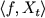 in three different regimes:
the small branching rate regime in three different regimes:
the small branching rate regime 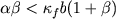 ;
the critical branching rate regime ;
the critical branching rate regime 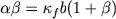 ;
and the large branching rate regime ;
and the large branching rate regime 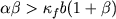 .
The talk is based on a joint work with Renming Song, Zhenyao Sun and Jianjie Zhao. .
The talk is based on a joint work with Renming Song, Zhenyao Sun and Jianjie Zhao.
|
|
René Schilling (Technische Universität Dresden):
The dimension walk and Schönberg's theorem revisited Schönberg's theorem asserts that a function 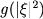 which is in any dimension the characteristic
function of an infinitely divisible random variable is of the form which is in any dimension the characteristic
function of an infinitely divisible random variable is of the form 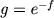 where f is a Bernstein function.
We give an elementary proof of this fact which is based on the "dimension walk",
that is concrete formulae which connect the transition densities and Lévy measures of subordinated
Brownian motions across different dimensions. As a by-product of our proof we obtain a gradient estimate
for the transition semigroup of a subordinated Brownian motion. where f is a Bernstein function.
We give an elementary proof of this fact which is based on the "dimension walk",
that is concrete formulae which connect the transition densities and Lévy measures of subordinated
Brownian motions across different dimensions. As a by-product of our proof we obtain a gradient estimate
for the transition semigroup of a subordinated Brownian motion.
|
|
Renming Song (University of Illinois):
Potential theory: subordination and killing In this talk I will survey some recent progress in the potential theory of Markov processes, with an emphasis on results related to subordination and killing, and results that Hrvoje and Zoran are part of. |
|
Fernando Soria (Universidad Autónoma de Madrid):
Dimension free estimates in Euclidean spaces In Analysis there are many inequalities in which finding the best constant for them to hold becomes a crucial issue. Examples of these are Hardy's and Sobolev's inequalities. In some other cases, when the problem may be stated in N-dimensional Euclidean space, the important thing is to know how the constants grow with (or, more precisely, depend on) the dimension. In this talk I will address a particular type of these problems, those in which the different constants are absolutely bounded, independent of the dimension. I will also present applications in some concrete examples as well as open problems and conjectures. |
|
Mladen Victor Wickerhauser (Washington University in St. Louis):
Wavelet Transform Factorization and Daubechies Filter Asymptotics Factorization of discrete wavelet transforms into lifting steps often exhibits the beneficial "nearest neighbor" property, with each factor affecting only adjacent signal samples. This property holds for the first factor of all sufficiently long Daubechies wavelets, and is conjectured to hold for all lifting factors of all Daubechies wavelets, but does not hold in general. The known results follow from careful asymptotic estimates on roots of Daubechies' polynomials. We will derive the estimates and show the behavior of the roots using computer graphics. (This is joint work with David Meyer and Matthew Stone.) |
Contributed talks
|
Ivana Geček Tuđen (University of Zagreb):
Generalized risk processes - a distributional equality for suprema of spectrally positive Lévy processes We are inspired by some interesting results for distribution of the supremum of the generalized risk process. Namely, if we observe a spectrally positive Lévy process Y with 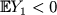 , an independent subordinator C with finite expectation
and the general process , an independent subordinator C with finite expectation
and the general process 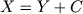 such that such that 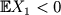 , then , then 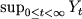 and the supremum of X just before the first time its new supremum is reached by a jump of C have the same distribution.
Using the Takács' formula, a fluctuation identity for spectrally one-sided Lévy processes and certain approximations of functions in Skorohod's
space
and the supremum of X just before the first time its new supremum is reached by a jump of C have the same distribution.
Using the Takács' formula, a fluctuation identity for spectrally one-sided Lévy processes and certain approximations of functions in Skorohod's
space 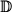 , we extend this result and explain why it is true. , we extend this result and explain why it is true.
|
|
Snježana Lubura Strunjak (University of Zagreb):
Local asymptotic mixed normality of approximate maximum likelihood estimator of drift parameters in diffusion model Let X be a diffusion which satisfies a stochastic differential equation of the form: 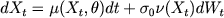 ,
where drift parameter ,
where drift parameter 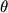 is unknown and diffusion coefficient parameter is unknown and diffusion coefficient parameter 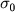 is known.
We have discrete observations is known.
We have discrete observations 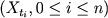 along fixed time interval [0,T].
Let along fixed time interval [0,T].
Let 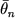 be approximate maximum likelihood estimator of drift parameter obtained
from discrete observations and let be approximate maximum likelihood estimator of drift parameter obtained
from discrete observations and let 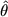 be maximum likelihood estimator obtained
from continuous observations be maximum likelihood estimator obtained
from continuous observations 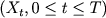 along fixed time interval [0,T].
We proved that along fixed time interval [0,T].
We proved that 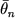 , when , when 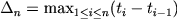 tends to zero,
is locally asymptotic mixed normal, with covariance matrix which depends on MLE tends to zero,
is locally asymptotic mixed normal, with covariance matrix which depends on MLE 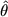 and on path
and on path 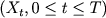 . .
|
|
Ivana Slamić (University of Rijeka):
Linear independence for systems generated by dual integrable representations Various important systems in harmonic analysis arise from an action of a countable discrete group. If the group acts on a Hilbert space via dual integrable representation, then, given any element of that Hilbert space, many properties of the corresponding system can be completely described in terms of the associated bracket. We consider the problem of finding characterizations of various levels of linear independence. In this talk, we mainly focus on the case of abelian groups. |
|
Stjepan Šebek (University of Zagreb):
CLT for the capacity of the range of stable random walks In this talk, we will establish a central limit theorem for the capacity of the range process for a class of d-dimensional symmetric alpha-stable random walks with the index satisfying 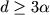 .
Our approach is based on controlling the limit behavior of the variance of the capacity of the range
process which then allows us to apply the Lindeberg-Feller theorem.
(The talk is based on the joint work with Wojciech Cygan and Nikola Sandrić.) .
Our approach is based on controlling the limit behavior of the variance of the capacity of the range
process which then allows us to apply the Lindeberg-Feller theorem.
(The talk is based on the joint work with Wojciech Cygan and Nikola Sandrić.)
|
|
Vanja Wagner (University of Zagreb):
Boundary behaviour of Markov processes corresponding to regional Dirichlet forms Let D be an open set in 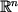 and
and 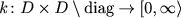 a symmetric measurable function such that a symmetric measurable function such that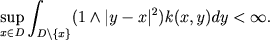 Let 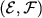 be a Dirichlet form on be a Dirichlet form on 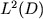 defined by defined by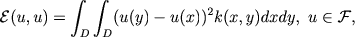 where 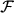 is the closure of is the closure of 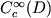 with respect to the norm
with respect to the norm 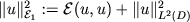 .
Since the Dirichlet form .
Since the Dirichlet form 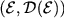 is regular by construction,
there exists a symmetric Hunt process Y corresponding to is regular by construction,
there exists a symmetric Hunt process Y corresponding to 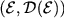 .
In order to analyze the boundary behaviour of Y, we consider the extended Dirichlet space .
In order to analyze the boundary behaviour of Y, we consider the extended Dirichlet space
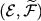 , ,
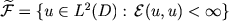 .
Since .
Since 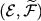 is a maximal Silverstein extension of the Dirichlet form is a maximal Silverstein extension of the Dirichlet form
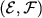 on on 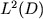 ,
there exists a symmetric Hunt process ,
there exists a symmetric Hunt process 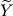 associated with associated with
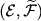 that extends Y to some state space that extends Y to some state space 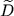 .
By using a trace theorem for Besov spaces of generalized smoothness we can show that,
for special types of kernels k and n-sets D, the extended process .
By using a trace theorem for Besov spaces of generalized smoothness we can show that,
for special types of kernels k and n-sets D, the extended process 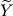 has state space
has state space 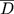 .
This means that we can interpret the symmetric Hunt process Y as the process .
This means that we can interpret the symmetric Hunt process Y as the process 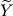 killed upon hitting the boundary
killed upon hitting the boundary 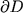 .
We will discuss the question of Y approaching the boundary .
We will discuss the question of Y approaching the boundary 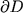 in finite time in terms of the polarity
of the boundary for the extended process in finite time in terms of the polarity
of the boundary for the extended process 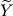 , as well as give conditions under
which , as well as give conditions under
which 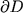 is polar for is polar for 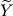 . .
|
Sponsors
 Croatian Science Foundation Research project UIP-2017-05-4129 Research project UIP-2017-05-8958 |
 Department of Mathematics Faculty of Science |
 Croatian Academy of Sciences and Arts |