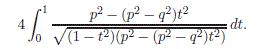
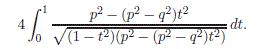
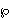 -funkcije.
Ova funkcija zadovoljava diferencijalnu jednadžbu oblika
-funkcije.
Ova funkcija zadovoljava diferencijalnu jednadžbu oblika
(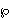 ')
') / 4 =
/ 4 =
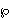
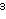 +
a
+
a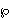 + b.
+ b.
Slično kao što jediničnu kružnicu možemo parametrizirati
pomoću (cos t, sin t), tako se kompleksne točke
na eliptičkoj krivulji y2 = x3 +
ax + b mogu parametrizirati pomoću
(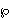 (t),
(t),
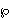 '(t)/2).
Štoviše, pokazuje se da ako je
P = (
'(t)/2).
Štoviše, pokazuje se da ako je
P = (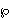 (t),
(t),
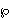 '(t)/2) i
Q = (
'(t)/2) i
Q = (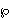 (u),
(u),
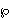 '(u)/2),
onda je P + Q =
(
'(u)/2),
onda je P + Q =
(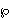 (t+u),
(t+u),
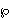 '(t+u)/2).
To znači da zbrajanje točaka na
E(
'(t+u)/2).
To znači da zbrajanje točaka na
E(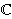 )
odgovara zbrajanju kompleksnih brojeva. Poznavanje te činjenice daje
elegantni dokaz asocijativnosti zbrajanja točaka na eliptičkoj
krivulji.
)
odgovara zbrajanju kompleksnih brojeva. Poznavanje te činjenice daje
elegantni dokaz asocijativnosti zbrajanja točaka na eliptičkoj
krivulji.
Kad se promatra nad poljem 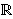 , eliptička krivulja je stvarno "krivulja", tj.
1-dimenzionalni objekt. No, promatrana nad
, eliptička krivulja je stvarno "krivulja", tj.
1-dimenzionalni objekt. No, promatrana nad
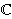 ona postaje
2-dimenzionalni objekt ("ploha") u 4-dimenzionalnom prostoru.
Pokušajmo vizualizirati tu plohu.
ona postaje
2-dimenzionalni objekt ("ploha") u 4-dimenzionalnom prostoru.
Pokušajmo vizualizirati tu plohu.
Tu nam može pomoći funkcija 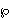 .
Ona posjeduje mnoga važna svojstva. Jedno njih jest da je
dvostruko periodična, tj. postoje kompleksni
brojevi
.
Ona posjeduje mnoga važna svojstva. Jedno njih jest da je
dvostruko periodična, tj. postoje kompleksni
brojevi 
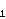 i
i

 (takvi da
(takvi da

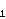 /
/

 nije realan broj) sa svojstvom
nije realan broj) sa svojstvom
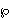 (z + m
(z + m

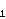 + n
+ n

 )
=
)
= 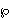 (z)
za sve cijele brojeve m, n.
Označimo s L "rešetku" svih točaka oblika
m
(z)
za sve cijele brojeve m, n.
Označimo s L "rešetku" svih točaka oblika
m

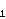 + n
+ n

 . Funkcija
. Funkcija
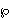 je analitička
u svim točkama kompleksne ravnine, osim u točkama iz
rešetke L u kojima ima pol drugog reda
(tj.
je analitička
u svim točkama kompleksne ravnine, osim u točkama iz
rešetke L u kojima ima pol drugog reda
(tj. 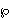 je
meromorfna funkcija). Općenito se meromorfne dvostruko
periodične funkcije nazivaju eliptičke funkcije.
je
meromorfna funkcija). Općenito se meromorfne dvostruko
periodične funkcije nazivaju eliptičke funkcije.
Gore navedena parametrizacija
točaka na eliptičkoj krivulji pomoću funkcije
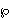 predstavlja zapravo
izomorfizam grupa
E(
predstavlja zapravo
izomorfizam grupa
E(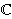 ) i
) i
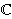 / L.
Funkcija
/ L.
Funkcija 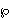 je u potpunosti određena svojim vrijednostima u "fundamentalnom
paralelogramu" koji se sastoji od svih kompleksnih brojeva
oblika m
je u potpunosti određena svojim vrijednostima u "fundamentalnom
paralelogramu" koji se sastoji od svih kompleksnih brojeva
oblika m

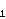 + n
+ n

 ,
0
,
0  m, n < 1.
m, n < 1.
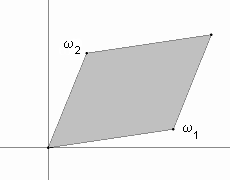
 / L.
Da bi vizualizirali taj skup,
možemo zamisliti da smo najprije "slijepili" dvije suprotne
stranice paralelograma. Tako dobivamo valjak. Nakon toga
"slijepimo" baze toga valjka. Tako dobivamo torus:
/ L.
Da bi vizualizirali taj skup,
možemo zamisliti da smo najprije "slijepili" dvije suprotne
stranice paralelograma. Tako dobivamo valjak. Nakon toga
"slijepimo" baze toga valjka. Tako dobivamo torus:


Ako krivulja ima stupanj n, onda je njezin genus
 (n - 1)(n - 2) / 2, s time da ako je
krivulja nesingularna, onda joj je genus upravo jednak
(n - 1)(n - 2) / 2.
Poznato je da takozvane hipereliptičke
krivulje čija je jednadžba y2 =
f(x), gdje je f(x) polinom stupnja
n
(n - 1)(n - 2) / 2, s time da ako je
krivulja nesingularna, onda joj je genus upravo jednak
(n - 1)(n - 2) / 2.
Poznato je da takozvane hipereliptičke
krivulje čija je jednadžba y2 =
f(x), gdje je f(x) polinom stupnja
n  3
bez višestrukih korijena, imaju genus
3
bez višestrukih korijena, imaju genus
 (n - 1)/2
(n - 1)/2![]](symbols/rfloor.gif) .
To posebno znači da, pored slučaja kada je n = 3,
i u slučaju kad je n = 4 također imamo eliptičku krivulju.
Uvjerimo se u to na jednom primjeru.
Neka je C krivulja zadana jednadžbom
.
To posebno znači da, pored slučaja kada je n = 3,
i u slučaju kad je n = 4 također imamo eliptičku krivulju.
Uvjerimo se u to na jednom primjeru.
Neka je C krivulja zadana jednadžbom
y2 = x4 + 3x2 + 2x.
Uvedimo supstituciju x = 2 / (s - 1), y = 2t / (s - 1)2. Inverzna transformacija je s = (x + 2) / x, t = 2y / x2. Stoga je ovo biracionalna transformacija. Ona prevodi krivulju C u eliptičku krivulju danu jednadžbomt2 = s3 - 3s + 6.
Krivulje genusa 0 su upravo one koje posjeduju parametrizaciju pomoću racionalnih funkcija. Svaka krivulja drugog stupnja (konika) ima genus 0. Npr. krivulja x2 + y2 = 1 ima racionalnu parametrizaciju
x = 2t / (t2 + 1), y = (t2 - 1) / (t2 + 1).
Kubne singularne krivulje također imaju genus 0. Npr. krivulja y2 = x3 ima singularnu točku (0,0). Stoga ova kubna krivulja nije eliptička. Njezina racionalna parametrizacija je x = t2, y = t3. Kao drugi primjer navedimo krivulju y2 = x3 + 2x2. Ona je također singularna i ima racionalnu parametrizaciju x = t2 - 2, y = t3 - 2t.
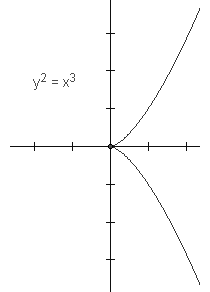
|
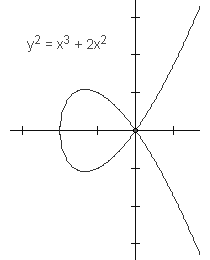
|
Očito je da ove dvije kubne krivulje imaju
beskonačno mnogo cjelobrojnih točaka. Pellova jednadžba
x2 - dy2 = 1
(d prirodan broj koji nije potpun kvadrat)
je primjer krivulje drugog stupnja koja ima beskonačno mnogo
cjelobrojnih točaka.
Krivulja genusa 1 može imati samo konačno mnogo cjelobrojnih točaka. Racionalnih točaka može biti beskonačno mnogo, ali su "konačno generirane" (sve se mogu dobiti iz konačno točaka primjenom grupovne operacije na eliptičkoj krivulji).
Krivulja genusa većeg od 1 može imati samo konačno mnogo racionalnih točaka. Ova tvrdnja je poznata Mordellova slutnja koju je 1983. godine dokazao Faltings.
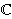 , a koliko
eliptička krivulja definirana nad
, a koliko
eliptička krivulja definirana nad
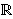 ?
O čemu sve ovisi odgovor za krivulje nad
?
O čemu sve ovisi odgovor za krivulje nad
 ?
?
y2 = x3 - 2x2 + x
ima genus 0, te nađite jednu njezinu racionalnu parametrizaciju.
| Web stranica seminara | Andrej Dujella - osobna stranica |