


Next: Array Sections
Up: Arrays
Previous: Whole Array Expressions
Consider the declaration
REAL, DIMENSION(1:6,1:8) :: P
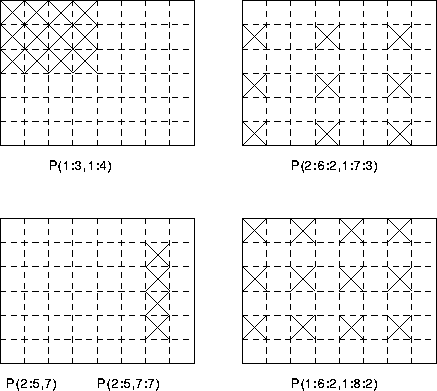
Figure 11: Visualisation of Array Sections
The sections:
- P(1:3,1:4) is a
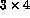 section; the missing stride
implies a value of 1,
section; the missing stride
implies a value of 1, - P(2:6:2,1:7:3), which could be written: P(2::2,:7:3))
is a
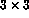 section.
section.
(A missing upper
bound (in the first dimension) means assume the upper bound as declared, (6),
A missing lower bound is the lower bound as declared, (1).)
- P(2:5,7) is a 1D array with 4 elements;
P(2:5,7:7) is a
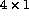 2D array,
2D array, - P(1:6:2,1:8:2) is a
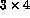 section. This could also be
written as P(::2,::2), here both upper and lower
bounds are missing so the values are taken to be the bounds as declared,
section. This could also be
written as P(::2,::2), here both upper and lower
bounds are missing so the values are taken to be the bounds as declared,
Conformance:
- P(1:3,1:4) = P(1:6:2,1:8:2) is a valid assignment; both LHS
and RHS are
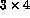 sections.
sections. - P(1:3,1:4) = 1.0 is a valid assignment; a scalar on the
RHS conforms to any array on the LHS of an assignment.
- P(2:6:2,1:7:3) = P(1:3,1:4) is not a valid assignment;
an attempt is made to equate a
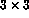 section with a
section with a 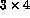 section, the array sections do not
conform.
section, the array sections do not
conform. - P(2:6:2,1:7:3) = P(2:5,7) is not a valid assignment;
an attempt is made to equate a
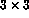 section with a 4 element 1D array.
section with a 4 element 1D array.
It is important to recognise the difference between an n element 1D
array and a 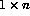 2D array:
2D array:
- P(2:5,7) is a 1D section -- the scalar in the second
dimension `collapses' the dimension.
- P(2:5,7:7) is a 2D section -- the second dimension is
specified with a section (a range) not a scalar so the resultant
sub-object is still two dimensional.
Return to corresponding overview page 



Next: Array Sections
Up: Arrays
Previous: Whole Array Expressions
©University of Liverpool, 1997
Wed May 28 20:20:27 BST 1997Not for commercial use.


![]() 2D array:
2D array:
![]()