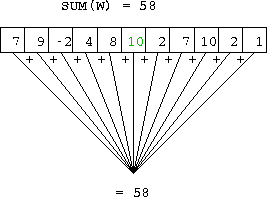
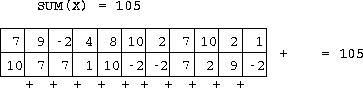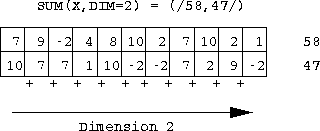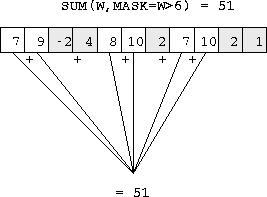- SUM returns the sum of array elements, along an optionally specified dimension under an optionally specified mask.
- if DIM is absent the whole array is considered and the result is
a scalar.
If DIM is not specified for the SUM of a 2D array then the result is obtained by adding all the elements together
- if DIM is specified the
result is an array of rank n-1 of sums, for example, summing down the
columns

Figure 19: Summing along Dimension 1 of a 2D Array
or along the rows,
- if MASK is present then the sum only involves elements
of SOURCE which correspond to .TRUE. elements of MASK, for example,
only the highlighted elements are considered,
- if the array is zero sized then the sum is 0
- PRODUCT returns the product of all array elements, along an optionally specified dimension under an optionally specified mask,
- if DIM is absent the whole array is considered and the result is a scalar.
- if DIM is specified the
result is an array of rank n-1 of products, for example,
if

PRINT*, PRODUCT(A,DIM=1) PRINT*, PRODUCT(A,DIM=2)
gives
2 12 30 15 48
- if MASK is present then the product only involves elements
of SOURCE which correspond to .TRUE. elements of MASK, for example,
PRINT*, PRODUCT(A,MASK=A.LT.4)
gives
6
- if the array is zero sized then the product is 1.
- ALL returns .TRUE. if all values of the mask
are .TRUE. (along an optionally specified) dimension DIM.
If DIM is specified then
the result is an array of rank n-1, otherwise a scalar is returned.
For example, consider a 2D array, if DIM=2 then the function returns a 1D vector with the result being as if the ALL function has been applied to each column in turn. If DIM=1 the result is as if the ALL function had been applied to each row in turn.
If A is as before, and

then the following
PRINT*, ALL(A.NE.B,DIM=1)
gives
T F F
recall that dimension 1 runs up and down the page.
Similarly
PRINT*, ALL(A.NE.B,DIM=2)
gives,
F F
where dimension 2 run across the page.
- if DIM is absent then the whole array is considered, for example,
PRINT*, ALL(A.NE.B)
gives the scalar value,
F
- if the array is zero sized then ALL returns .TRUE.,
- ANY returns .TRUE. if any values of the mask are
.TRUE. (along an optionally specified dimension DIM). If DIM is
given then the result is an array of rank n-1, for example,
PRINT*, ANY(A.NE.B,DIM=1) PRINT*, ANY(A.NE.B,DIM=2)
gives
T F T T T
- if DIM is absent then the whole array is considered, for
example,
PRINT*, ANY(A.NE.B)
gives the scalar value,
T
- if the array is zero sized then ANY returns .FALSE..
- COUNT returns the number of .TRUE. elements in a specified
LOGICAL array along
dimension DIM. The result is an array of rank n-1, for example,
PRINT*, COUNT(A.NE.B,DIM=1) PRINT*, COUNT(A.NE.B,DIM=2)
gives
2 0 1 1 2 - if DIM is absent then the whole array is considered, for
example,
PRINT*, COUNT(A.NE.B)
gives the scalar,
3
- if the array is zero sized then COUNT returns zero.
- MAXVAL returns the maximum values in an array along an optionally specified dimension under an optionally specified mask,
- if DIM is specified the
result is an array of rank n-1 of maximum values in other dimensions,
for example,
PRINT*, MAXVAL(A,DIM=1) PRINT*, MAXVAL(A,DIM=2)
gives
2 4 6 5 6 - if DIM is absent the whole array is considered and the result is a scalar.
- if MASK is present then the survey is only performed on elements
of SOURCE which correspond to .TRUE. elements of MASK, for example,
PRINT*, MAXVAL(A,MASK=A.LT.4)
only considers elements of A that are less than 4 and gives
3
- the largest negative number of the appropriate kind is returned if
the array is zero sized.
- MINVAL returns the minimum value in an array along an optionally specified dimension under an optionally specified mask,
- if DIM is specified the
result is an array of rank n-1 of minimum values in other dimensions,
for example,
PRINT*, MINVAL(A,DIM=1) PRINT*, MINVAL(A,DIM=2)
gives
1 3 5 1 2 - if DIM is absent the whole array is considered and the result is a scalar.
- if MASK is present then the survey is only performed on elements
of SOURCE which correspond to .TRUE. elements of MASK, for example,
PRINT*, MINVAL(A,MASK=A.GT.4)
gives
5
- the smallest positive number of the appropriate kind is returned if
the array is zero sized.