Grafovi dobiveni od konačnih ravnina
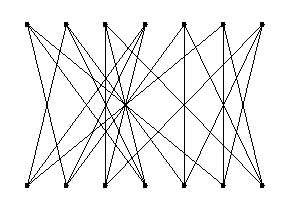
Konačnoj (projektivnoj) ravni možemo pridružiti graf na sljedeći način:
Vrhovi grafa neka su točke i pravci ravnine. Vrhovi A i b spojeni su bridom
akko je A točka koja leži na pravcu b. Ova konstrukcija je provediva i na
blok dizajnima, ne samo na ravninama.
Ako na opisani način pridružimo graf G konačnoj projektivnoj ravnini P
reda n, on će biti (n+1)-regularan, bipartitan i imat će "struk" (girth) 6.
Ukupan broj vrhova grafa G je 2(n^2+n+1). Grupa automorfizama od G izomorfna
je punoj grupi kolineacija i korelacija ravnine P. Ako izbacimo automorfizme
koji preslikavaju točke na pravce ("korelacije"), dobivamo grupu kolineacija
od P.
Posljednje svojstvo posebno je zgodno, jer postoji program koji brzo računa
automorfizme grafa: nauty
(autor je B.D.McKay).
Evo nekoliko primjera grafova dobivenih od ravnina, u formatu za Mathematica
paket Combinatorica (učitavanje sa ReadGraph) i za dreadnaut, korisnički
interface za nauty:
Program nauty je izuzetno efikasan za Desarguesove ravnine. Npr. za ravninu
reda devet generatori pune grupe kolineacija dobiju se za oko 30 sekundi
(na HP 9000/800). Ta grupa je reda 84913920 !
Vedran Krcadinac, 5.6.1996.
