Predgovor

Steinerovi 2-dizajni proučavaju se više od 150 godina. Njihovo ime donekle je nepravedno vezano uz švicarskog geometričara J.Steinera, jer ih je prije njega uveo engleski matematičar T.P.Kirkman. Da nepravda bude veća, Kirkman je u članku iz 1847. riješio problem egzistencije za k = 3, dok je Steiner samo postavio problem 1853. godine (ne znajući za Kirkmanov rad).

Sredinom 20. stoljeća ponovo oživljava interes za slične konačne strukture. Poticaj djelomično dolazi iz biologije i drugih eksperimentalnih znanosti, gdje se dizajni koriste za planiranje eksperimenata. U šezdesetim godinama H.Hanani riješio je problem egzistencije Steinerovih 2-dizajna za k = 4 i k = 5. Najveći napredak ostvaren je u sedamdesetim godinama, kad je R.M.Wilson dokazao da su nužni uvjeti egzistencije ujedno i ``asimptotički dovoljni'', za svaki k ł 3.

Tema ovog rada su Steinerovi 2-dizajni s parametrima S(k,2k²-2k+1). Oni su među Steinerovim 2-dizajnima karakterizirani svojstvom da pravaca ima dvostruko više nego točaka, ili određenom ``hiperboličkom negacijom'' Euklidovog petog postulata. Mogli bi ih stoga zvati konačne hiperboličke ravnine. Problem egzistencije tih dizajna otvoren je za svaki k ł 6, jer su parametri izvan dosega Wilsonove asimptotičke teorije. Danas su poznata svega 34 primjera s k = 3, 4 i 5.

U prvom dijelu rada detaljno proučavamo poznate primjere. Promatramo njihove pune grupe automorfizama, poddizajne i skoro-rezolucije. Osim toga dokazujemo neka svojstva zajednička svim S(k,2k²-2k+1) dizajnima, posebno njihove veze s drugim konačnim strukturama - simetričnim (2k²-3k+1)_k konfiguracijama i eliptičkim poluravninama.

U sklopu rada razvijamo algoritam za klasifikaciju konačnih objekata do na izomorfizam. Algoritam su E.Spence i drugi koristili u mnogim posebnim slučajevima. U radu algoritam opisujemo i dokazujemo na općenit način. Razvijamo niz programskih alata za provedbu algoritma i primjenjujemo ga na klasifikaciju Steinerovih 2-dizajna S(3,13), S(3,15) i S(4,25). Osim toga razrađujemo primjenu algoritma na orbitne strukture, što nam kasnije omogućuje konstrukciju novih S(5,41) dizajna.

Najveći dio rada posvećen je upravo pokušajima konstrukcije novih S(k, 2k²-2k+1) dizajna. Koristimo dvije osnovne metode, konstrukciju pomoću diferencijskih familija i konstrukciju pomoću grupa automorfizama. Prvom metodom dobivamo uglavnom negativne rezultate. Među njima su dva nova, nepostojanje (113,8,1) diferencijske familije i nepostojanje radikalnih (2k²-2k+1,k,1) diferencijskih familija za 6 Ł k Ł 2000. Drugom metodom dobivamo devet novih S(5,41) dizajna, pretpostavivši djelovanje grupe automorfizama reda 3. U dokazu je algoritam za klasifikaciju odigrao ključnu ulogu, zbog izuzetno velikog broja neizomorfnih orbitnih struktura. Također dobivamo niz negativnih rezultata za k = 6, 7 i 8, na primjer nepostojanje S(6,61) dizajna s grupom automorfizama reda 25.

Velik broj dokaza u radu zasniva se na proračunima na računalu. Radu je priložen CD koji sadrži korištene programe, pisane u programskom jeziku C. Na CD-u su pohranjeni rezultati i međurezultati proračuna, često preveliki da bi ih u cijelosti reproducirali na papiru. Na CD-u se nalazi i tekst rada u PDF i HTML formatu, koji sadrži veze (linkove) na relevantne datoteke. Na primjer, kad govorimo o dizajnu S3.1, ime je vezano uz tablicu u kojoj su sabrana njegova svojstva. Preko tablice možemo pristupiti mjestu gdje je dizajn pohranjen u obliku incidencijske matrice ili u drugom obliku.

Za nastanak rada zaslužni su mnogi pojedinci, kojima bih na ovom mjestu želio izraziti zahvalnost. Prvenstveno zahvaljujem voditelju rada, dr. Jurju Šiftaru na pozornom praćenju mog rada još od studentskih dana. Pod njegovim sam vodstvom napisao diplomski rad, kao i studentski rad nagrađen Rektorovom nagradom. Zahvaljujem dr. Mariu Pavčeviću na velikom interesu koji je pokazao za rad i na mnogim korisnim sugestijama i primjedbama. Dio rada nastao je za vrijeme studijskog boravka na Sveučilištu u Glasgowu. Zahvaljujem dr. Tedu Spenceu na ljubaznosti i gostoprimstvu, a British Scholarship Trust-u i Ministarstvu znanosti i tehnologije na financiranju boravka. Zahvaljujem članovima Geometrijskog seminara, na kojem sam u obliku predavanja izložio velik dio rada.

Na ``prženju'' CD-a zahvaljujem dr. Goranu Igalyju, a na pomoći pri tiskanju rada Matiji Baliću. Zahvaljujem voditelju i osoblju Računskog centra na pruženoj podršci, kao i cjelokupnom ``računalno orijentiranom'' dijelu Matematičkog odjela na toleriranju mojih sveprisutnih programa koji usporavaju sustav. Zahvaljujem supruzi Jeleni na strpljivom podnošenju tipkanja po tastaturi u kasne sate, a roditeljima i bratu na žustrom bodrenju bez kojeg bi rad sigurno nastao puno kasnije.

Sadržaj

1  Uvod

1.1  Osnovni rezultati teorije dizajna

Definicija 1 Incidencijska struktura sastoji se od skupa točaka P, skupa pravaca L i relacije incidencije I Í P ×L. Ako je (T,l) Î I kažemo da točka T leži na pravcu l, odnosno da l prolazi kroz T i pišemo T I l.

Napomena 2 Skup svih točaka koje leže na pravcu l označavamo (l). Za incidencijsku strukturu kod koje su skupovi tog oblika međusobno različiti kažemo da je jednostavna. Pravce jednostavne incidencijske strukture možemo identificirati s pripadnim skupovima točaka, a I s relacijom ``biti element''  Î . U daljnjem ćemo pod incidencijskom strukturom uvijek razumijevati jednostavnu incidencijsku strukturu.

Definicija 3 Za incidencijsku strukturu kažemo da je t-(v,k,l) dizajn ako ima svojstva:

(1)

Ukupni broj točaka je v.

(2)

Svaki pravac sadrži k točaka.

(3)

Svaki t-člani skup točaka sadržan je u l pravaca.

Napomena 4 Da bi izbjegli trivijalne primjere u ovom radu promatramo samo dizajne s t < k < v. Dizajni se najviše proučavaju u dva specijalna slučaja, t = 2 i l = 1. Dizajne s t = 2 zovemo 2-dizajni ili blok dizajni. U tom slučaju pravci se obično nazivaju blokovi, a parametri bilježe (v,k,l). Dizajne s l = 1 zovemo Steinerovi sistemi, a parametre zapisujemo u obliku S(t,k,v). Dizajne koji pripadaju jednoj i drugoj familiji (s parametrima 2-(v,k,1)) zovemo Steinerovi 2-dizajni S(k,v).

Propozicija 5 Ako je incidencijska struktura t-(v,k,l) dizajn, onda je i s-(v,k,l_s) dizajn, za

Dokaz. Neka je (P,L, Î ) t-(v,k,l) dizajn, a S Í P bilo koji s-člani skup točaka. Prebrojimo na dva načina elemente skupa

Napomena 6 l₀ je broj pravaca koji sadrže prazan skup, dakle ukupan broj pravaca. Označavamo ga b. l₁ je broj pravaca kroz bilo koju točku, koji označavamo r.

Korolar 7 Za (v,k,l) blok dizajn vrijedi

Definicija 8 Neka su P = { T₁,...,T_v } točke, a L = {l₁,...,l_b} pravci incidencijske strukture. Incidencijska matrica te strukture je v ×b matrica

Propozicija 9 Neka je A Î M_vb({0,1}) v ×b matrica s unosima 0 ili 1. A je incidencijska matrica (v,k,l) blok dizajna ako i samo ako zadovoljava

(1)

A ·A^t = (r-l) I_v + lJ_v

(2)

J_v ·A = k J_v,b

Pritom je I_v jedinična matrica reda v, a J_v i J_v,b matrice čiji su svi unosi jedinice, dimenzija v×v i v ×b.

Dokaz. Uvjet (2) ekvivalentan je svojstvu da pravci sadrže po k točaka. Uvjet (1) ekvivalentan je svojstvima da je svaka točka sadržana u r pravaca, a svaki par točaka u l pravaca.

Propozicija 10 [Fisherova nejednakost] Broj točaka (v,k,l) blok dizajna nije veći od broja pravaca, v Ł b.

Dokaz. Incidencijska matrica A blok dizajna zadovoljava

Korolar 11 Parametri Steinerovog 2-dizajna S(k,v) zadovoljavaju

Dokaz. Slijedi iz Fisherove nejednakosti i korolara 1.7.

Napomena 12 Fisherova nejednakost je nuždan uvjet za postojanje
t-(v,k,l) dizajna (t ł 2). Drugi nuždan uvjet je da su brojevi

1.2  Djelovanje grupa

Definicija 13 Neka je G grupa s neutralnim elementom 1, a X skup. Kažemo da G djeluje na X ako je zadana funkcija G×X --> X, (g,x) --> gx takva da za svaki x Î X i g,h Î G vrijedi 1x = x i g(hx) = (gh)x.

Napomena 14 Točnije, kažemo da grupa G djeluje na skup X s lijeva. Djelovanje zdesna je funkcija X ×G --> X sa svojstvima x 1 = x i x(gh) = (xg)h, za svaki x Î X, g,h Î G. Pod pojmom djelovanja razumijevamo djelovanje s lijeva, osim ako naglasimo suprotno.

Napomena 15 Ako je g = 1 jedini element sa svojstvom gx = x, za svaki x Î X, kažemo da je djelovanje vjerno. U suprotnom možemo definirati normalnu podgrupu N = { g Î G | gx = x, za svaki x Î X } i zamijeniti G s kvocijentnom grupom. G/N uz prirodnu definiciju također djeluje na X, i to vjerno. U ovom radu sva djelovanja bit će vjerna.

Primjer 16 Svaka grupa (G,·) djeluje na samu sebe, uz definiciju (g,h) --> g ·h. Takvo djelovanje zovemo lijevim translacijama. G djeluje lijevim translacijama i na partitivni skup P(G). Budući da se pritom čuva kardinalni broj, G također djeluje na skup k-članih podskupova P_k(G).

Definicija 17 Neka G djeluje na X i neka je x Î X. Stabilizator od x je podgrupa G_x = { g Î G | gx = x } < G. Staza ili orbita od x je skup x^G = { gx | g Î G } Í X.

Propozicija 18 Kardinalni broj orbite jednak je indeksu stabilizatora, |x^G| = [G:G_x]. U konačnom slučaju to je ekvivalentno s |G| = |G_x|·|x^G|.

Dokaz. Vrijedi gx = hx Ű (h^-1g)x = x Ű h^-1g Î G_x Űg i h pripadaju istoj lijevoj klasi modulo G_x. Zato je gG_x ® gx dobro definirana bijekcija sa skupa lijevih klasa na orbitu x^G.

Lema 19 [Burnside] Neka G djeluje na konačan skup X. Ako s n označimo broj orbita, a s f(g) broj elemenata skupa { x Î X | gx = x }, onda vrijedi

Dokaz. Prebrojimo na dva načina članove skupa

Definicija 20 Neka je S = (P,L,I) incidencijska struktura. Za grupu G koja djeluje na točke i pravce tako da vrijedi T I lŰ gT I gl, za g Î G, T Î P, l Î L kažemo da je grupa automorfizama od S.

Definicija 21 Incidencijske strukture S₁ = (P₁,L₁,I₁), S₂ = (P₂, L₂,I₂) su izomorfne ako postoje bijekcije j: P₁ -->P₂, y: L₁ -->L₂ koje čuvaju incidenciju, tj. takve da za P Î P₁, l Î L₁ vrijedi P I₁ lŰ j(P) I₂ y(l). Par (j,y) zovemo izomorfizam. Skup svih izomorfizama s incidencijske strukture S na samu sebe zovemo puna grupa automorfizama od S i označavamo Aut(S).

Propozicija 22 Aut(S) je grupa automorfizama od S. Svaka grupa automorfizama od S ulaže se u Aut(S).

Dokaz. Aut(S) djeluje na točke i pravce na prirodan način,

2  Steinerovi 2-dizajni S(k,2k²-2k+1)

2.1  Osnovna svojstva i primjeri

Tema ovog rada je jedna familija Steinerovih 2-dizajna. Na slici 1 prikazani su dopustivi parametri S(k,v) za 3 Ł k Ł 15 i 5 Ł v Ł 215.

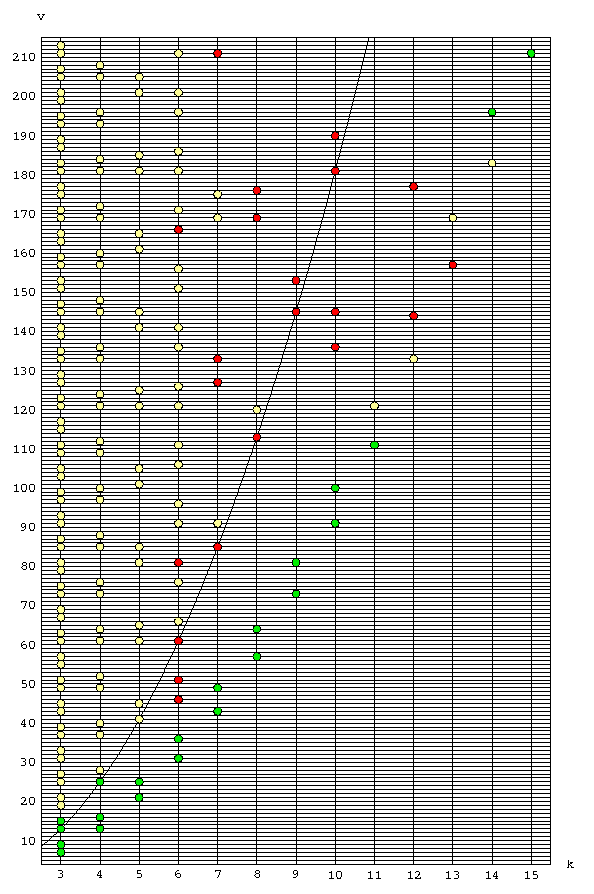
Zelenom bojom označeni su parametri za koje je provedena klasifikacija (tj. poznat je točan broj dizajna s tim parametrima). Žutom bojom označeni su parametri za koje dizajni postoje, a crvenom parametri za koje je problem egzistencije otvoren.

Parametri dizajna koje proučavamo leže na paraboli v = 2k²-2k+1. Dopustivi su za svaki k ł 3. Vidimo da su dizajni klasificirani za k = 3 i 4, postoje za k = 5, a za k ł 6 ne zna se da li postoje. Osim preko parametara možemo ih karakterizirati na još nekoliko načina.

Propozicija 1 Steinerov 2-dizajn ima parametre oblika S(k,2k²-2k+1) ako i samo ako je ispunjen bilo koji od sljedećih uvjeta:

(1)

Broj pravaca dvostruko je veći od broja točaka (b = 2v).

(2)

Broj pravaca kroz bilo koju točku dvostruko je veći od broja točaka na bilo kojem pravcu (r = 2k).

(3)

Za bilo koju točku T i pravac l koji nisu incidentni, broj pravaca kroz T koji sijeku l jednak je broju pravaca kroz T disjunktnih s l.

Dokaz. Parametri Steinerovog 2-dizajna zadovoljavaju

U sljedećoj tablici navedeni su svi poznati Steinerovi 2-dizajni S(k,2k²-2k+1). U elektroničkoj verziji ovog dokumenta unosi u tablici ujedno su linkovi na odgovarajuće objekte.

Prvi stupac sadrži oznaku dizajna i njegov prikaz u tri formata: kao skup pravaca (m), kao incidencijska matrica (inc) i kao bipartitni graf (dre). Graf je zapisan u obliku koji prepoznaje dreadnaut, sučelje za nauty. To je program pomoću kojeg možemo izračunati punu grupu automorfizama dizajna (vidi str. 31).

Drugi stupac sadrži apstraktan prikaz pune grupe automorfizama i njezin red. Grupe su analizirane pomoću programa GAP [17], sustava za računalnu algebru specijaliziranog za diskretne algebarske strukture. Unos u drugom stupcu vezan je uz datoteku u GAP-formatu koja sadrži grupu.

U trećem i četvrtom stupcu navedeni su multiskupovi duljina staza na točkama, odnosno pravcima (pod djelovanjem pune grupe automorfizama). Izračunati su također pomoću programa dreadnaut.

U tablici smo za opis strukture pune grupe automorfizama koristili niz oznaka. Direktan produkt grupa označavamo križićem `×', a semidirektan produkt točkom. Slijede oznake za grupe korištene u tablici:

Zn	-	ciklička grupa reda n
D2n	-	diedralna grupa reda 2n
PSLn(q)	-	projektivna specijalna linearna grupa (kvocijent grupe n×n
		matrica determinante 1 nad GF(q) s njezinim centrom, ska-
		larnim matricama)
An	-	alternirajuća grupa stupnja n (na n slova)
Q8	-	kvaternionska grupa reda 8

2.2  Podstrukture

Definicija 2 Neka je S = (P,L,I) incidencijska struktura. Za S˘ = (P˘,L˘,I˘) kažemo da je podstruktura od S ako je P˘ Í P, L˘ Í L i I˘ = I Ç(P˘×L˘). Ako je P˘ Ě P kažemo da je S˘ prava podstruktura od S.

U situaciji kad je zadana incidencijska struktura S i njezina podstruktura S˘ točke i pravce podstrukture zovemo nutarnjim. Pravce koji ne pripadaju podstrukturi ali prolaze kroz neku nutarnju točku zovemo rubni pravci, a preostale vanjski pravci. Dualno, točku koja ne pripada podstrukturi zovemo rubna točka ako leži na nekom pravcu podstrukture, a inače vanjska točka.

Definicija 3 Za podstrukturu dizajna kažemo da je poddizajn ako je i sama dizajn.

Poddizajni Steinerovih 2-dizajna također su Steinerovi 2-dizajni. Neka su v, b, r, k parametri Steinerovog 2-dizajna, a v˘, b˘, r˘, k˘ njegovog poddizajna. Očito vrijedi v˘ Ł v i k˘ Ł k. Promotrimo najprije slučaj k = k˘.

Propozicija 4 Ako Steinerov 2-dizajn S(k,v) ima pravi poddizajn S(k,v˘), onda je v˘ Ł r.

Dokaz. Promotrimo pravce kroz točku T koja ne pripada poddizajnu. Na svakom od njih leži najviše jedna točka poddizajna. U suprotnom bi pravac bio nutarnji, pa bi zbog k = k˘ točka T pripadala poddizajnu. Zato broj točaka poddizajna nije veći od broja pravaca kroz T, v˘ Ł r.

Propozicija 5 Steinerov 2-dizajn S(k,2k²-2k+1) ne može imati pravi poddizajn s parametrima S(k,v˘).

Dokaz. Pretpostavimo da postoji poddizajn S(k,v˘). Iz korolara 1.11 primjenjenog na poddizajn i iz prethodne propozicije dobivamo

U općenitoj situaciji (k˘ Ł k) vrijede sljedeće ocjene za broj točaka pravog poddizajna.

Lema 6 Neka je S˘ pravi poddizajn Steinerovog 2-dizajna S. Tada vrijedi:

Dokaz. Označimo broj nutarnjih, rubnih i vanjskih pravaca redom s b_N, b_R i b_V. Prema korolaru 1.7 vrijedi

Pomoću prethodne leme možemo odrediti koji su poddizajni načelno mogući u dizajnima sa zadanim parametrima. Promotrimo pobliže poznate dizajne iz serije koju proučavamo, S(3,13), S(4,25) i S(5,41).

Propozicija 7 Steinerovi 2-dizajni S(3,13) nemaju pravih poddizajna.

Dokaz. Slijedi iz propozicije 2.5.

Propozicija 8 Ako Steinerov 2-dizajn S(4,25) ima pravi poddizajn, njegovi parametri su S(3,7) (tj. radi se o projektivnoj ravnini reda dva).

Dokaz. Poddizajni S(4,v˘) nisu mogući zbog 2.5. Za poddizajne S(3,v˘) iz leme 2.6 dobivamo ocjene v˘ Ł 17 i (v˘)²-25v˘+150 ł 0. Nejednakosti zadovoljavaju tri dopustiva v˘, 7, 9 i 15.

U slučaju poddizajna S(3,15) broj vanjskih pravaca bio bi b_V = 0 (vidi dokaz leme 2.6). Neka je T točka koja ne pripada poddizajnu. Označimo broj nutarnjih pravaca kroz T s r_N, a rubnih s r_R. Vanjskih pravaca nema, pa je r_N + r_R = r = 8. Rubni pravci sadrže po jednu točku poddizajna, a nutarnji po tri, iz čega slijedi 3r_N + r_R = v˘ = 15. Rješavanjem jednadžbi dobivamo kontradikciju, r_N = ⁷/₂ i r_R = ⁹/₂. Dakle, ne postoje S(3,15) poddizajni.

Za poddizajn S(3,9) ukupni broj vanjskih pravaca je b_V = 2. Neka su r_N, r_R i r_V broj nutarnjih, rubnih i vanjskih pravaca kroz točku T koja ne pripada poddizajnu. Brojevi zadovoljavaju r_N + r_R + r_V = r = 8 i 3r_N + r_V = v˘ = 9, iz čega oduzimanjem slijedi 2r_N = 1+r_V. Očito je 0 Ł r_V Ł b_V = 2; broj r_N je prirodan samo za r_R = 1. Dakle, kroz proizvoljnu ne-nutarnju točku prolazi točno jedan vanjski pravac. To je kontradikcija, jer dva vanjska pravca mogu pokriti najviše 8 od ukupno v-v˘ = 16 točaka izvan poddizajna.

Preostaje jedino mogućnost poddizajna S(3,7).

U tablici 2 vidimo koliko stvarno ima poddizajna u pojedinim S(4,25) dizajnima. Rezultati su dobiveni programom subsearch, koji sustavno traži poddizajne sa zadanim parametrima.

Propozicija 9 Ako Steinerov 2-dizajn S(5,41) ima pravi poddizajn, njegovi parametri su S(3,7), S(3,9), S(3,19) ili S(3,21).

Dokaz. Zbog propozicije 2.5 ne postoje poddizajni S(5,v˘). Lema 2.6 za S(4,v˘) daje ocjene v˘ Ł 31 i (v˘)²-41v˘+328 ł 0, koje ne zadovoljava ni jedan dopustivi v˘. Za poddizajne S(3,v˘) dobivamo samo jedan uvjet, v˘ Ł 21. Dolaze u obzir v˘ = 7,9,13,15,19 i 21.

Obzirom na poddizajn S(3,15) dva pravca su vanjska (b_V = 2). Kao i u dokazu propozicije 2.8, neka su r_N, r_R i r_V broj nutarnjih, rubnih i vanjskih pravaca kroz neku točku izvan poddizajna. Vrijedi r_N + r_R + r_V = r = 10 i 3r_N + r_R = v˘ = 15. Oduzimanjem dobivamo 2r_N = 5 + r_V, iz čega slijedi r_V = 1 (jer r_N mora biti prirodan i 0 Ł r_V Ł b_V = 2). Dakle, kroz svaku točku koja ne pripada poddizajnu prolazi jedan vanjski pravac. To je kontradikcija jer dva vanjska pravca pokrivaju najviše 10 točaka.

U slučaju poddizajna S(3,13) broj vanjskih pravaca je b_V = 4. Brojevi r_N, r_R i r_V zadovoljavaju r_N + r_R + r_V = 10 i 3r_N + r_R = 13, iz čega slijedi 2r_N = 3 + r_V. Sad je 0 Ł r_V Ł 4, pa imamo dvije mogućnosti: r_V = 1 ili r_V = 3. Označimo s v₁ broj točaka izvan poddizajna kroz koje prolazi jedan vanjski pravac, a s v₂ broj točaka kroz koje prolaze tri vanjska pravca. Očito je v₁ + v₂ = v - v˘ = 28. Prebrojavanjem incidentnih parova (točka izvan poddizajna, vanjski pravac) slijedi v₁ + 3v₂ = b_V ·k = 20. Rješavanjem dobivamo kontradikciju, v₂ = -4. Dakle, ne postoje niti S(3,13) poddizajni.

U tablici 3 vidimo broj S(3,7) i S(3,9) poddizajna u poznatim S(5,41) dizajnima. Program subsearch nažalost nije dovoljno brz za prebrojavanje S(3,19) i S(3,21) poddizajna.

Među podstrukturama Steinerovog 2-dizajna poddizajni su karakterizirani sljedećim uvjetima:

(a)

Na pravcima podstrukture leži konstantan broj točaka podstrukture.

(b)

Kroz točke podstrukture prolazi konstantan broj pravaca podstrukture.

(c)

Svake dvije točke podstrukture spojene su pravcem koji pripada podstrukturi.

Zanemarivanjem posljednjeg uvjeta dolazimo do podstruktura koje su konfiguracije.

Definicija 10 Za incidencijsku strukturu od v točaka i b pravaca kažemo da je (v_r,b_k) konfiguracija ako zadovoljava:

(1)

Na svakom pravcu leži k točaka.

(2)

Kroz svaku točku prolazi r pravaca.

(3)

Svake dvije točke spojene su najviše jednim pravcem.

Nužni uvjeti postojanja (v_r,b_k) konfiguracije su vr = bk i v ł r(k-1)+1. Ako je v = b (ili ekvivalentno r = k) kažemo da je konfiguracija simetrična i parametre bilježimo v_r.

Definicija 11 Neka je S = (P,L,I) incidencijska struktura, a l Î L pravac. Podstruktura S^(l) sastoji se od točaka P˘ = P \(l) i pravaca L˘ = { l˘ Î L | l i l˘ su disjunktni }.

Propozicija 12 U Steinerovom 2-dizajnu S s parametrima v, b, r, k podstruktura S^(l) je ((v-k)_r-k, (b-k(r-1)-1)_k) konfiguracija.

Dokaz. Broj točaka u S^(l) očito je |P| - |(l)| = v-k. Kroz svaku točku na l prolazi još r-1 pravaca, pa l siječe ukupno k(r-1) pravaca (i naravno sam sebe). Pravci podstrukture su oni koji ne sijeku l; ima ih b-k(r-1)-1.

Kroz svaku točku podstrukture prolazi r-k pravaca podstrukture (od ukupno r pravaca njih k su spojnice s točkama na l). Pravci podstrukture disjunktni su s l, pa sve točke na njima pripadaju podstrukturi. Dakle, svaki pravac podstrukture sadrži k točaka podstrukture.

Konačno, uvjet (3) iz definicije konfiguracije zadovoljen je u svakoj podstrukturi Steinerovog 2-dizajna.

Korolar 13 Steinerov 2-dizajn S ima parametre oblika S(k,2k²-2k+1) ako i samo ako su konfiguracije S^(l) simetrične. Parametri tih konfiguracija su (2k²-3k+1)_k.

Propozicija 14 Neka pravci l₁ i l₂ incidencijske strukture S pripadaju istoj orbiti pod djelovanjem pune grupe automorfizama Aut(S). Tada su konfiguracije S^(l₁) i S^(l₂) izomorfne.

Dokaz. Neka je S^(l₁) = (P₁,L₁,I₁) i S^(l₂) = (P₂,L₂,I₂). Po pretpostavci postoji automorfizam a Î Aut(S) takav da je l₂ = a(l₁). Funkcije a|_P1 :P₁ --> P₂ i a|_L1 : L₁ --> L₂ su dobro definirane bijekcije, a par (a|_P1,a|_L1) izomorfizam između S^(l₁) i S^(l₂).

Obrat propozicije ne vrijedi. U dizajnu S3.2 postoje pravci koji induciraju izomorfne konfiguracije, ali pripadaju različitim orbitama.

Definicija 15 Neka je C (v_r,b_k) konfiguracija. Konfiguracijski graf G(C) ima za vrhove točke od C, a za bridove parove točaka koje nisu spojene pravcem u C.

Graf (v_r,b_k) konfiguracije je d-regularan, za d = v-r(k-1)-1. Parametar d naziva se defekt. Konfiguracije defekta nula podudaraju se sa Steinerovim 2-dizajnima.

Definicija 16 Neka je C simetrična (2k²-3k+1)_k konfiguracija. Rastav na klike konfiguracijskog grafa G(C) je particija skupa vrhova na potpune podgrafove K_k-1. Za dva rastava na klike kažemo da su ortogonalni ako ne sadrže isti brid od G(C).

Teorem 17 [Gropp] Simetrična (2k²-3k+1)_k konfiguracija C je oblika C = S^(l) za neki Steinerov 2-dizajn S ako i samo ako graf G(C) dopušta k međusobno ortogonalnih rastava na klike.

Dokaz. Pretpostavimo da je C = S^(l) za pravac l Steinerovog 2-dizajna S(k,2k²-2k+1). Svakoj točki T na l odgovara rastav na klike grafa G(C): pravci kroz T (različiti od l) čine particiju konfiguracije na 2k-1 blokova od po k-1 točaka. Unutar jednog bloka točke nisu spojene pravcima konfiguracije, jer su spojene pravcem koji siječe l (u točki T). Prema tome, blokovi su potpuni podgrafovi grafa G(C).

Rastavi na klike koji odgovaraju dvjema različitim točkama su ortogonalni. U suprotnom bi sadržali isti brid grafa G(C), tj. neki blok prvog rastava i neki blok drugog rastava imali bi dvije zajedničke točke. To bi značilo da se odgovarajući pravci sijeku u dvije točke, što u Steinerovom 2-dizajnu nije moguće.

Za obrat neka su R⁽ⁱ⁾ = { B⁽ⁱ⁾₁,..., B⁽ⁱ⁾_2k-1 }, i = 1,...,k međusobno ortogonalni rastavi na klike grafa G(C). Proširujemo konfiguraciju točkama 1,2,...,k, pravcem l = {1,...,k} i pravcima B⁽ⁱ⁾_j Č{ i }. Za nove pravce incidencija je relacija pripadanja  Î . Pokazuje se da je proširena struktura S Steinerov 2-dizajn S(k,2k²-2k+1) i da je C = S^(l).

Napomena 18 Prema [6], H.Gropp je teorem izložio 1986. na kombinatoričkoj konferenciji u Cataniji (Italija). Predložio je klasifikaciju S(4,25) dizajna pomoću simetričnih konfiguracija 21₄.

Gropp je proveo klasifikaciju za k = 3. Najprije je klasificirao konfiguracije 10₃, kojih ima ukupno 10 (među njima je Desarguesova konfiguracija). Zatim ih je, koristeći teorem 2.17 proširivao do S(3,13) dizajna. Jednu od konfiguracija moguće je proširiti do S3.1 i S3.2, jedna se proširuje samo do S3.1, šest samo do S3.2, a dvije (uključujući Desarguesovu) nije moguće proširiti. Zaključujemo da su S3.1 i S3.2 jedini S(3,13) dizajni.

Međutim, čini se da ideja nije provediva za k = 4, zbog prevelikog broja neizomorfnih 21₄ konfiguracija. Dizajne S(4,25) klasificirao je E.Spence 1996. godine, na drugi način (vidi 3.26).

Steinerove 2-dizajne S(k,2k²-2k+1) možemo pomoću (2k²-3k+1)_k konfiguracija organizirati u graf G. Vrhovi grafa su neizomorfni S(k,2k²-2k+1) dizajni. Vrhovi S₁ i S₂ spojeni su bridom ako postoje pravci l₁ u S₁ i l₂ u S₂ takvi da su konfiguracije S₁^(l₁) i S₂^(l₂) izomorfne. Očito je svaki vrh spojen sam sa sobom, tj. graf G sadrži sve petlje. Nadalje, povezani mogu biti samo dizajni s istim parametrima. Poznati dio grafa prikazan je na slici 2.

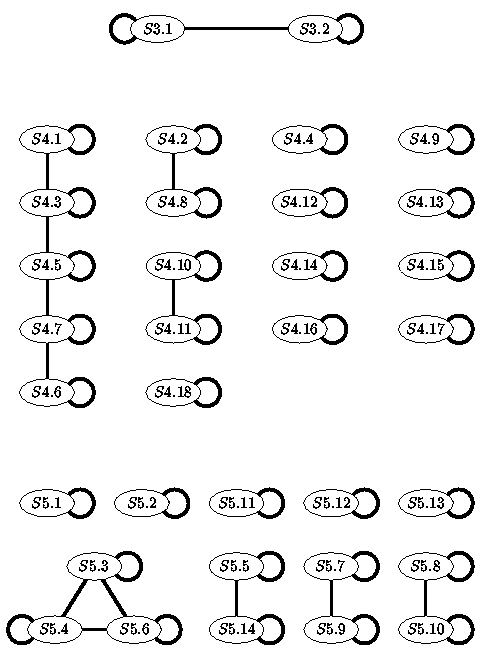
Na sličan način definiramo graf G^d. Vrhovi S₁ i S₂ spojeni su bridom ako su konfiguracije S₁^(l₁) i (S₂^(l₂))^d izomorfne, za pravce l₁ iz S₁ i l₂ iz S₂. Pritom je C^d dualna konfiguracija od C, dobivena zamjenom uloge točaka i pravaca (transponiranjem incidencijske matrice). Poznati dio grafa vidimo na slici 3.

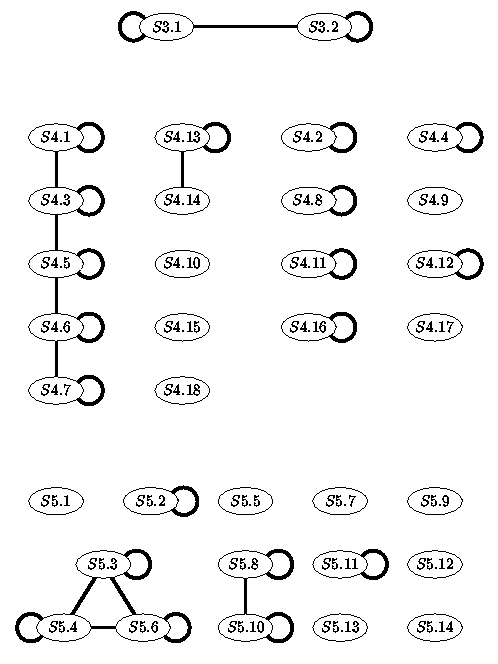
Od poznatog dizajna S možemo konstruirati sve dizajne u istoj komponenti povezanosti grafa G ili G^d. Konstruiramo konfiguracije S^(l) (ili njima dualne), eliminiramo izomorfne i preostale konfiguracije proširujemo na sve moguće načine do S(k,2k²-2k+1) dizajna. Tako dobivamo dizajne koji su sa S povezani bridom u G ili G^d. Postupak ponavljamo dok ne prijeđemo čitavu komponentu povezanosti.

Napisao sam niz programa za provedbu tog postupka. Program extract konstruira incidencijske matrice konfiguracija, a incfilter propušta samo neizomorfne (vidi str. 32). Za proširivanje konfiguracija napisao sam program embed. Program traži ortogonalne rastave na klike konfiguracijskog grafa i primjenjuje konstrukciju iz teorema 2.17. S algoritamskog stanovišta problem se svodi na višestruko traženje klika (potpunih podgrafova) u prikladno definiranim grafovima. Prvo tražimo (k-1)-klike u konfiguracijskom grafu. U drugom koraku definiramo graf čiji su vrhovi pronađene (k-1)-klike, pri čemu su bridom spojene one koje su disjunktne. Klika od 2k-1 vrhova u tom grafu ekvivalentna je rastavu na klike konfiguracijskog grafa. Konačno, definiramo graf čiji su vrhovi rastavi na klike, a bridovi parovi međusobno ortogonalnih rastava na klike. U trećem koraku tražimo k-klike u tom grafu, što nam daje skupove od k međusobno ortogonalnih rastava na klike konfiguracijskog grafa.

Postupak je već za k = 5 prilično dugotrajan, ali broj konfiguracija koje treba proširivati nije prevelik. Od dizajna S možemo dobiti najviše onoliko neizomorfnih konfiguracija koliko je Aut(S)-orbita na pravcima, i isto toliko dualnih (propozicija 2.14).

Na ovaj način prvi put su konstruirani neki od S(4,25) dizajna. Prema [8], A.Y.Petrenyuk je konstruirao dizajne povezane sa S4.1, S4.2 i S4.3 i tako dobio četiri nova dizajna. A.Rosa i R.Mathon konstruirali su jedan novi S(5,41) dizajn. Krenuli su od dizajna koji posjeduju automorfizam reda 5 (vidi teorem 5.31) i dobili dizajn S5.4. Primjenom transformacije na dizajne prvi put konstruirane u ovom radu (teorem 5.33) ne dobivaju se novi S(5,41) dizajni.

2.3  Paralelizam i rezolucije

Za pravce incidencijske strukture kažemo da su paralelni ako se podudaraju ili ako nemaju zajedničkih točaka. Dualno, točke su paralelne ako se podudaraju ili ako nisu spojene pravcem. U Steinerovom 2-dizajnu ne postoje parovi paralelnih točaka, ali mogu postojati parovi paralelnih pravaca.

Definicija 19 Neka je S = (P,L,I) incidencijska struktura. Klasa paralelizma u S je skup međusobno paralelnih pravaca koji čine particiju skupa P (tj. pokrivaju sve točke). Rezolucija od S je particija skupa pravaca L na međusobno disjunktne klase paralelizma. Za incidencijsku strukturu koja dopušta rezoluciju kažemo da je rješiva.

Pretpostavimo da u Steinerovom 2-dizajnu S(k,v) postoji klasa paralelizma. Očito tada k dijeli v. Ako postoji rezolucija, broj pravaca u klasi paralelizma  v/k dijeli ukupni broj pravaca b. Tako dobivamo nužne uvjete za postojanje rješivog S(k,v) dizajna, v ş 0 (mod k) i v ş 1 (mod k-1). Parametri ih zadovoljavaju ako i samo ako su oblika S(k,k(mk-m+1)).

Uvrštavanjem m = 1 dobivamo parametre afinih ravnina S(k,k²). Poznato je da svaka afina ravnina ima jedinstvenu rezoluciju. Najmanji dopustivi parametri za rješivi Steinerov 2-dizajn koji nije afina ravnina su S(3,15). Postoji 80 takvih dizajna (primjer 3.25), od čega je 4 rješivo. T.P.Kirkman je u svom poznatom problemu 15 djevojčica zapravo tražio rješive S(3,15) dizajne.

Parametri dizajna koje proučavamo, S(k,2k²-2k+1) ne zadovoljavaju nužne uvjete za rješivost. Modificirat ćemo pojam rezolucije tako da bude prikladan za naše dizajne.

Definicija 20 Neka je S = ( P,L,I) incidencijska struktura, a T Î P točka. Skoro-klasa paralelizma u S je skup međusobno paralelnih pravaca koji čine particiju skupa P\{ T} (tj. pokrivaju sve točke osim T). Skoro-rezolucija od S obzirom na T je particija skupa pravaca koji ne sadrže T (L\(T)) na međusobno disjunktne skoro-klase paralelizma. Za incidencijsku strukturu koja dopušta skoro-rezoluciju kažemo da je skoro-rješiva (obzirom na T).

Ako u Steinerovom 2-dizajnu postoji skoro-klasa paralelizma, k dijeli v-1. Ako postoji skoro-rezolucija, (v-1)/k dijeli b-r. Slijede nužni uvjeti za skoro-rješivost Steinerovog 2-dizajna, v ş 1 (mod k) i v ş 1 (mod k-1). Parametri ih zadovoljavaju ako i samo ako su oblika S(k,mk²-mk+1).

Uvrštavanjem m = 1 dobivamo parametre projektivnih ravnina S(k,k²-k+1). Za razliku od afinih ravnina koje su rješive, projektivne ravnine nisu skoro-rješive. Svaka dva pravca projektivne ravnine sijeku se u jednoj točki, pa uopće ne postoje parovi paralelnih pravaca.

Za m = 2 dobivamo parametre dizajna koje proučavamo, S(k,2k²-2k+1). Tablica 4 sadrži podatke o broju skoro-klasa paralelizma i skoro-rezolucija u svim poznatim primjerima.

Vidimo da je jedino dizajn S4.1 skoro-rješiv, i to samo obzirom na specijalnu točku koja je orbita pune grupe automorfizama. Podaci u tablici dobiveni su pomoću programa nrsearch. Problem pronalaženja (skoro) rezolucija svodi se na dvostruko traženje klika, slično kao u programu embed. Da bi našli sve (skoro) klase paralelizma tražimo klike u grafu čiji su vrhovi pravci, a bridovi parovi paralelnih pravaca. Drugi put tražimo klike u grafu čiji su vrhovi (skoro) klase paralelizma. Bridom su spojene klase koje su međusobno disjunktne.

Definicija 21 Neka su R = {P₁,...,P_n} i R˘ = {P˘₁,...,P˘_n} (skoro) rezolucije incidencijske strukture S, pri čemu su P_i, P˘_j (skoro) klase paralelizma. Kažemo da su R i R˘ ortogonalne ako vrijedi |P_i ÇP˘_j| Ł 1, za sve i,j = 1,...,n.

Steinerovi 2-dizajni S(k,2k²-2k+1) s dovoljnim brojem međusobno ortogonalnih skoro-rezolucija u vezi su s vrlo zanimljivim konačnim strukturama, tzv. eliptičkim poluravninama.

Definicija 22 Eliptička (v,k) poluravnina je incidencijska struktura koja zadovoljava aksiome:

(1)

Ukupni broj točaka je v.

(2)

Na svakom pravcu leži k točaka i kroz svaku točku prolazi k pravaca.

(3)

Svake dvije točke spojene su najviše jednim pravcem.

(4)

Za svaku točku T i pravac l koji nisu incidentni najviše jedan pravac kroz T paralelan je s l i najviše jedna točka na l paralelna je s T.

Napomena 23 Prebrojavanjem incidentnih parova vidimo da je ukupni broj pravaca također v. Očito vrijedi i dual aksioma (3) (svaka dva pravca sijeku se najviše u jednoj točki). Prema tome, dualna struktura je također eliptička (v,k) poluravnina. Eliptičke poluravnine mogli smo kraće definirati kao simetrične v_k konfiguracije koje zadovoljavaju samodualni aksiom (4). Primjeri eliptičkih poluravnina su konačne projektivne ravnine i strukture koje od njih dobivamo izbacivanjem Baerovih (gustih) zatvorenih podstruktura.

Napomena 24 U incidencijskoj strukturi pod stupnjem točke (pravca) podrazumijevamo broj s njom incidentnih pravaca (točaka). Red strukture je maksimalni stupanj umanjen za jedan. P.Dembowski je u knjizi [5] definirao poluravninu kao incidencijsku strukturu koja zadovoljava aksiome (3) i (4) i u kojoj je svaki element stupnja bar tri. Pokazao je da u konačnoj poluravnini reda n skup stupnjeva svih elemenata može biti samo { n-1,n,n+1}, {n,n+1} ili {n+1}. U prvom slučaju poluravnine je nazvao hiperboličkim, u drugom paraboličkim, a u trećem eliptičkim. Red eliptičke (v,k) poluravnine je n = k-1.

Važnu ulogu pri rasvjetljavanju veze eliptičkih poluravnina i S(k, 2k²-2k+1) dizajna igra vrlo općenita klasa incidencijskih struktura, koje se na engleskom zovu ``group divisible designs''. U hrvatskom se još nije ustalio naziv, pa ćemo koristiti samo njihove parametre GDD_l(k,g,v). Nažalost način zapisivanja parametara nije kod svih autora isti. Koristimo oblik iz knjige [2].

Definicija 25 Za incidencijsku strukturu kažemo da je GDD_l(k,g,v) ako vrijedi:

(1)

Ukupni broj točaka je v.

(2)

Svaki pravac sadrži k točaka.

(3)

Postoji particija skupa točaka na blokove duljine g takva da su parovi točaka iz različitih blokova spojeni s l pravaca, a parovi točaka iz istog bloka nisu spojeni pravcem.

Blokove particije iz (3) zovemo grupe. Ako je l = 1, parametre bilježimo GDD(k,g,v). Ako je ukupni broj pravaca također v, govorimo o simetričnom GDD_l(k,g,v).

Primjer 26 Promotrimo incidencijsku strukturu dobivenu punktiranjem Steinerovog 2-dizajna, tj. uklanjanjem jedne točke i svih pravaca koji kroz nju prolaze. Ukupni broj točaka smanjen je na v-1, ali broj točaka na svakom od preostalih pravaca i dalje je k. Uklonjeni pravci particioniraju preostale točke na r grupa duljine k-1, tako da je zadovoljeno svojstvo (3) za l = 1. Prema tome, radi se o GDD(k,k-1,v-1).

Obrnuto, ako krenemo od strukture GDD(k,k-1,v-1), nadodamo jednu novu točku, te grupe proširimo novom točkom i proglasimo novim pravcima, dobit ćemo Steinerov 2-dizajn S(k,v). Klasama paralelizma i rezolucijama strukture GDD(k,k-1,v-1) odgovaraju skoro-klase paralelizma i skoro-rezolucije dizajna S(k,v) obzirom na uklonjenu/nadodanu točku.

Teorem 27 Incidencijska struktura je eliptička (v,k) poluravnina ako i samo ako je simetrični GDD(k,g,v). Pritom je g = v-k(k-1).

Dokaz. Prvo dokazujemo da je eliptička (v,k) poluravnina simetrični GDD(k,g,v). Treba samo provjeriti svojstvo (3), postojanje particije skupa točaka na grupe. Zbog aksioma (4) iz definicije eliptičke poluravnine paralelizam je relacija ekvivalencije. Za grupe uzmimo klase ekvivalencije na točkama. Kroz bilo koju točku T prolazi k pravaca, a na svakom leži još k-1 točaka. Znači, k(k-1) točaka nije paralelno s T, tj. proizvoljna grupa sadrži g = v - k(k-1) točaka. Točke iz iste grupe nisu spojene pravcima (jer su paralelne), a točke iz različitih grupa u parovima su spojene po jednim pravcem (jer nisu paralelne). Dakle, imamo simetrični GDD(k,g,v).

Dokazujemo obrat, da je simetrični GDD(k,g,v) eliptička (v,k) poluravnina. Očito su ispunjeni aksiomi (1) i (3). Za aksiom (2) treba vidjeti da kroz svaku točku prolazi k pravaca. Proizvoljna točka T spojena je pravcem sa svim točkama koje nisu u istoj grupi, njih v-g. Na svakom pravcu kroz T leži osim T još k-1 točaka. Dakle, kroz T prolazi (v-g)/(k-1) pravaca. Prebrojavanjem incidentnih parova slijedi

Još treba provjeriti aksiom (4). Neka je zadana točka T i pravac l koji nisu incidentni. Dvije točke koje nisu spojene pravcem s T leže u istoj grupi, pa ni međusobno nisu spojene pravcem. Zato najviše jedna od njih može ležati na l. Dakle, najviše jedna točka na l paralelna je s T, pa je najmanje k-1 točaka na l spojeno s T. Drugačije rečeno, bar k-1 pravaca kroz T siječe l, a to opet znači da je najviše jedan pravac kroz T paralelan s l. Dakle, struktura je eliptička (v,k) poluravnina.

Teorem 28 [Lamken, Vanstone] Eliptička (v,k) poluravnina s g < k-1 postoji ako i samo ako postoji GDD(k-g,g,(k-1)(k-g)) s g međusobno ortogonalnih rezolucija, za g = v-k(k-1).

Dokaz. Neka je S eliptička (v,k) poluravnina i g < k-1. Primjenom prethodnog teorema na dualnu strukturu (koja je također eliptička (v,k) poluravnina) slijedi da pravce možemo podijeliti na grupe duljine g unutar kojih su međusobno paralelni pravci. Odaberimo jednu grupu {l₁,...,l_g}. Neka je S˘ podstruktura od S dobivena brisanjem odabranih pravaca i točaka koje na njima leže. Tvrdimo da je S˘ GDD(k-g,g,(k-1)(k-g)).

Izbrisali smo kg točaka, pa je u S˘ ostalo v-kg = k(k-1)+g-kg = (k-1)(k-g) točaka. Pravci iz S˘ sijeku svaki od izbrisanih pravaca, jer ne pripadaju odabranoj grupi. Slijedi da na svakom pravcu iz S˘ leži k-g točaka iz S˘. Nadalje, točka podstrukture spojena je sa svim izbrisanim točkama, pa grupa kojoj pripada leži cijela u S˘. Dakle, S˘ je GDD(k-g,g,(k-1)(k-g)).

Pramen pravaca kroz svaku od izbrisanih točaka (bez pripadnog izbrisanog pravca) je klasa paralelizma u S˘. Klase paralelizma koje odgovaraju izbrisanim točkama na istom izbrisanom pravcu međusobno su disjunktne. Slijedi da svaki izbrisani pravac određuje rezoluciju podstrukture S˘. Tako dobivenih g rezolucija u parovima je ortogonalno. Dvije točke s dva različita izbrisana pravca spojene su najviše jednim pravcem, pa pripadne klase paralelizma imaju najviše jedan zajednički pravac.

Obrnuto, neka je S GDD(k-g,g,(k-1)(k-g)) i neka su R⁽ⁱ⁾ = { P⁽ⁱ⁾₁,..., P⁽ⁱ⁾_k }, i = 1,...,g međusobno ortogonalne rezolucije (P⁽ⁱ⁾_j su klase paralelizma). Proširimo S točkama P⁽ⁱ⁾_j, uz definiciju P⁽ⁱ⁾_j I l Ű l Î P⁽ⁱ⁾_j. Nadodajmo još R⁽¹⁾,...,R^(g) kao nove pravce, uz `` Î '' kao relaciju incidencije. Pokazuje se da je proširena struktura simetrični GDD(k,g,v), odnosno eliptička (v,k) poluravnina.

Prethodni teorem dokazan je u [11]. Jedan smjer dokazali su još prije R.D.Baker i G.L.Ebert.

Korolar 29 Steinerov 2-dizajn S(k,2k²-2k+1) s k-1 međusobno ortogonalnih skoro-rezolucija (obzirom na istu točku) postoji ako i samo ako postoji eliptička ((4k-1)(k-1),2k-1) poluravnina.

Dokaz. Prema teoremu 2.28 postojanje eliptičke ((4k-1)(k-1),2k-1) poluravnine ekvivalentno je postojanju GDD(k,k-1,2k²-2k) s k-1 međusobno ortogonalnih rezolucija. U primjeru 2.26 vidjeli smo da je to ekvivalentno postojanju S(k,2k²-2k+1) dizajna s k-1 međusobno ortogonalnih skoro-rezolucija.

Primjer 30 Dizajn S4.1 posjeduje 11 skoro-rezolucija, među njima 3 ortogonalne. Punktiranjem u specijalnoj točki dobivamo GDD(4,3,24) s 3 međusobno ortogonalne rezolucije. Prema teoremu 2.28, iz njega možemo konstruirati eliptičku (45,7) poluravninu s g = 3. Poluravnina je samodualna i ima A₇ . Z₃ kao punu grupu automorfizama (reda 7560). Ta grupa djeluje tranzitivno na točke i pravce.

Napomena 31 Glavno pitanje o poluravninama kojim se bavio Dembowski u [5] tiče se njihovog ulaganja u projektivne ravnine. Za hiperboličke i paraboličke poluravnine Dembowski je dokazao da se uvijek ulažu u odgovarajuću projektivnu ravninu. Za eliptičke (v,k) poluravnine dokazao je da vrijedi g = k, g = k-1 ili g Ł k - Ök. U prva dva slučaja i ako se u trećem slučaju dostiže jednakost uspio je dokazati da se poluravnina ulaže u projektivnu ravninu reda k. Dembowski je postavio hipotezu da eliptičke poluravnine s 1 < g < k - Ök ne postoje.

R.D.Baker [1] je 1977. godine konstruirao protuprimjer, eliptičku (45,7) poluravninu. Njegova poluravnina izomorfna je poluravnini iz primjera 2.30, iako nije dobivena na isti način. Osim Bakerovog primjera poznata je samo još jedna eliptička poluravnina s 1 < g < k-Ök. Radi se o eliptičkoj (135,12) poluravnini, a konstruirao ju je R.Mathon.

3  Klasifikacija

U ovom poglavlju dokazujemo pomoću računala da Steinerovih 2-dizajna S(k,2k²-2k+1) ima točno dva za k = 3 i točno osamnaest za k = 4. Algoritam za klasifikaciju je objašnjen u općenitom kontekstu jer na analogan način u petom poglavlju konstruiramo orbitne strukture. Prvi dio poglavlja posvećen je kanonskom preslikavanju, koje igra ključnu ulogu u algoritmu. Opisani su alati za računanje kanonskih predstavnika i pune grupe automorfizama. U drugom dijelu opisan je algoritam za klasifikaciju i njegova primjena na Steinerove 2-dizajne i orbitne strukture.

3.1  Kanonsko preslikavanje

Na početku uvodimo nazive i oznake koje ćemo koristiti u cijelom poglavlju. Neka je X skup objekata na kojem djeluje grupa G. Za objekte A, B Î X kažemo da su izomorfni i pišemo A @ B ako postoji g Î G takav da je B = gA, tj. ako pripadaju istoj stazi. Stabilizator G_A = { g Î G | gA = A } zovemo puna grupa automorfizama objekta A i označavamo Aut(A).

Primjer 1 Neka je X skup svih incidencijskih struktura sa skupom točaka P = {1,...,v} i skupom pravaca L = {1,...,b}. Na njemu djeluje direktni produkt simetričnih grupa G = S_v×S_b, tako da relaciju incidencije I Í P ×L preslika u (p,s)I = { (p(i),s(j)) | (i,j) Î I }, za (p,s) Î G. Izomorfnost i puna grupa automorfizama obzirom na ovo djelovanje podudaraju se s pojmovima definiranim u uvodu (1.21). Umjesto X možemo uzeti G-invarijantan podskup X˘ Í X, na primjer Steinerove 2-dizajne S(k,v).

Primjer 2 Neka je X = M_mn(N₀) skup svih m×n matrica nad N₀. Grupa G = S_m ×S_n na njemu djeluje permutiranjem redaka i stupaca. Za (p,s) Î G i A = [ a_ij ] Î X slika (p,s)A = B = [b_ij ] definirana je s b_p(i)s(j) = a_ij. Umjesto X možemo uzeti manji, G-invarijantan skup matrica, na primjer incidencijske matrice Steinerovih 2-dizajna S(k,v).

Primjer 3 Obojani graf sastoji se od konačnog skupa V, familije dvočlanih podskupova B Í P₂(V) i funkcije b : V --> N. Elemente iz V zovemo vrhovi, elemente iz B bridovi, a b bojanje. Neka je X skup svih obojanih grafova sa skupom vrhova V = {1,...,n}, a G simetrična grupa S_n. Djelovanje G na X definiramo formulom p(B,b) = (pB,b °p^-1), gdje je pB = { {p(i),p(j)} | {i,j} Î B }. Tako dobivamo uobičajene pojmove izomorfnosti i pune grupe automorfizama za grafove, uz uvjet da se samo vrhovi iste boje smiju preslikati jedni na druge.

Definicija 4 Kanonsko preslikavanje je svaka funkcija c:X --> X koja ima svojstva

(1)

c(A) @ A, za svaki A Î X

(2)

c(gA) = c(A), za svaki g Î G, A Î X

Fiksne točke kanonskog preslikavanja zovemo kanonski objekti ili kanonski predstavnici obzirom na c.

Propozicija 5 Ako je c : X --> X kanonsko preslikavanje, vrijedi

Dokaz. (Ţ) Ako je A izomorfan s B, postoji g Î G takav da je B = gA. Slijedi c(A) = c(gA) = c(B).

(Ü) Ako je c(A) = c(B), vrijedi A @ c(A) = c(B) @ B.

Propozicija 6 Neka je zadan totalni uređaj na skupu objekata X na kojem djeluje konačna grupa G. Tada je funkcija c:X --> X, c(A) = max { gA | g Î G } kanonsko preslikavanje.

Dokaz. Funkcija je dobro definirana jer su staze { gA | g Î G } konačni skupovi, pa maksimumi postoje. Očito c zadovoljava svojstva (1) i (2) iz definicije 3.4.

Cilj ove točke je razviti algoritam za računanje kanonskog preslikavanja iz prethodne propozicije. Najjednostavniji algoritam je petlja koja prelazi po svim g Î G i pamti najveći među objektima gA. U praksi to nije provedivo jer grupa G ima previše elemenata. Razvit ćemo brži algoritam u specijalnom slučaju matrica nad N₀ (primjer 3.2). Treba nam totalni uređaj na skupu matrica X = M_mn(N₀).

Definicija 7 Neka su A = [a_ij], B = [b_ij] Î M_mn(N₀). Kažemo da je matrica A manja od matrice B i pišemo A < B ako postoji par indeksa (i₀,j₀) Î {1,...,m} ×{1,...,n} takav da vrijedi a_{i0 j0} < b_{i0 j0} i a_ij = b_ij, za i = 1,...,i₀-1, j = 1,...,n i za i = i₀, j = 1,...,j₀-1. Ako je A < B ili A = B kažemo da je A manja ili jednaka od B i pišemo A Ł B.

Drugim riječima, uspoređujemo obzirom na leksikografski uređaj vektore dobivene spajanjem redaka matrice. Nije teško provjeriti da je definirana relacija totalni uređaj na skupu X = M_mn(N₀).

Da bismo opisali algoritam i dokazali njegovu valjanost trebaju nam neke oznake i činjenice. Neka je V_i skup svih injekcija sa skupa {1,...,i} u skup {1,...,m}. Elemente iz V_i bilježimo kao uređene i-torke; (p₁,...,p_i) je injekcija koja pridružuje k --> p_k, k = 1,...,i. Elementi iz V_m su permutacije stupnja m, tj. V_m = S_m. Definiramo preslikavanje (A,p) --> Ap Î M_in(N₀),

Propozicija 8 Neka su A,B Î M_mn(N₀). Ako je A Ł B, onda je A(1,...,i) Ł B(1,...,i), za svaki i = 1,...,m.

Dokaz. Slijedi iz definicije uređaja među matricama 3.7.

Propozicija 9 Kad god je za p Î V_i, s Î V_j definirana kompozicija p°s, vrijedi A(p°s) = (Ap)s.

Dokaz. Označimo

Iz propozicije 3.9 slijedi da je (A,p) --> Ap djelovanje grupe V_m = S_m na skup X = M_mn(N₀) zdesna. Veza s djelovanjem grupe G = S_m ×S_n definiranim u 3.2 je Ap = (p^-1,id)A.

Skup

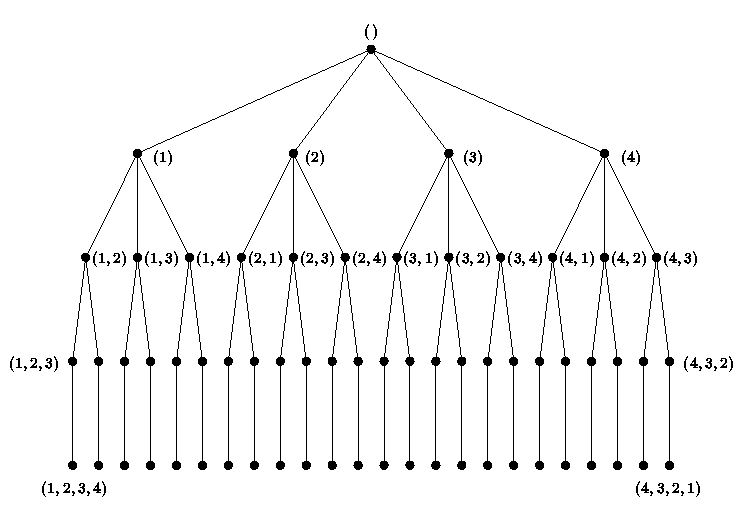
Algoritam za računanje kanonskog predstavnika matrice pretražuje dio tog stabla po širini (breadth-first search). Da bismo formulirali algoritam trebaju nam oznake za roditelja i djecu vrhova stabla.

Neka je r : V --> V funkcija definirana s r(p) = p|_{1,...,i-1} , za p Î V_i. Funkcija pridružuje vrhu p njegovog roditelja u stablu. Neka je d:P(V) --> P(V), d(W) = r^-1(W). Funkcija d skupu W Í V pridružuje skup djece vrhova iz W. Nadalje, neka je sort(A) najveća matrica dobivena permutiranjem stupaca matrice A, tj.  sort(A) = max{ (id,s)A | s Î S_n }. Do nje dolazimo silaznim sortiranjem stupaca od A obzirom na leksikografski uređaj.

Algoritam 10 [kanonsko preslikavanje]

Tvrdimo da je C_m koji se ispisuje na kraju algoritma jednak kanonskom predstavniku c(A). Označimo C_i = max{ sort)(Ap) | p Î V_i }, K_i = { p Î V_i | sort(Ap) = C_i }.

Lema 11 Matrica C_i sastoji se od prvih i redaka kanonske matrice c(A), C_i = c(A)(1,...i).

Dokaz. Primijetimo najprije da je

Da bi dokazali obratnu nejednakost neka je p Î K_i, tj. C_i = sort(Ap). Postoje s Î S_n i r Î S_m takvi da je sort(Ap) = (id,s)Ap i p = r|_{1,...,i}. Znamo da je c(A) ł (r^-1,s)A, iz čega zbog propozicije 3.8 slijedi

Dakle, C_i = c(A)(1,...,i).

Lema 12 Ako je p Î K_i, onda je r(p) Î K_i-1.

Dokaz. Označimo r = r(p) = p°(1,...,i-1). Vrijedi:

Lema 13 Nakon izvođenja algoritma 3.10 vrijedi C_i = C_i i K_i = K_i, za svaki i = 1,Ľ,m.

Dokaz. Indukcijom po i. Za i = 1 algoritam prelazi po svim p Î d( () ) = V₁ i pamti najveću matricu oblika sort(Ap). Zato je C₁ = C₁ i K₁ = K₁.

Pretpostavimo da tvrdnja vrijedi za i-1, tj. C_i-1 = C_i-1 i K_i-1 = K_i-1. Algoritam u i-tom koraku pamti najveću od matrica sort(Ap) za p Î d(K_i-1) = d(K_i-1). Za preostale p Î V_i matrice sort(Ap) su prema lemi 3.12 manje od C_i. Vidimo da se u C_i sprema najveća matrica oblika sort(Ap), pa je C_i = C_i i K_i = K_i.

Teorem 14 Matrica C_m koju ispisuje algoritam 3.10 jednaka je kanonskom predstavniku matrice A.

Dokaz. C_m = (lema 3.13) = C_m = (lema 3.11) = c(A)(1,...,m) = c(A).

Algoritam 3.10 realiziran je u programu canonmat, pisanom u programskom jeziku C. Osim za računanje kanonskog predstavnika možemo ga upotrijebiti za određivanje pune grupe automorfizama matrice.

Propozicija 15 Neka su stupci matrice A međusobno različiti. Tada je skup K_m = { p Î S_m | sort(Ap) = c(A) } definiran algoritmom 3.10 u bijektivnom odnosu s punom grupom automorfizama  Aut(A).

Dokaz. Za matricu A postoji jedinstveni s Î S_n takav da je sort(A) = (id,s)A. Ista tvrdnja vrijedi za matrice Ap, p Î S_m, jer su i njihovi stupci međusobno različiti. Definiramo bijekciju između K_m i skupa K = { (p,s) Î S_m ×S_n | (p,s)A = c(A) }. Elementu p Î K_m pridružujemo par (p^-1,s), gdje je s Î S_n jedinstvena permutacija za koju je sort(Ap) = (id,s)Ap. Skup K je lijeva klasa pune grupe automorfizama Aut(A) (vrijedi K = (p₀,s₀)Aut(A), za bilo koji (p₀,s₀) Î K). Vidimo da je K_m bijektivan s lijevom klasom K, koja je bijektivna s Aut(A).

Glavni nedostatak algoritma 3.10 je što stablo pretražuje po širini. Zato je potrebno pamtiti skupove K₁,...,K_m, koji za pravilne matrice (kao što su incidencijske matrice dizajna) vrlo brzo postaju preveliki za memoriju računala. Postoje algoritmi koji stablo pretražuju po dubini (depth-first search, backtracking), na primjer [12] i [13]. Na taj način ne moraju se pamtiti veliki skupovi vrhova. Osim toga automorfizmi se pronalaze u ranijoj fazi potrage, pa ih se može upotrijebiti za smanjivanje dijela stabla kojeg treba pretražiti. Takvi algoritmi pamte skup generatora pune grupe automorfizama, a ne sve njezine elemente.

Jedan od najbržih programa tog tipa je nauty B.D.McKay-a [14]. Program računa kanonskog predstavnika i punu grupu automorfizama obojanog grafa (primjer 3.3). Možemo ga primijeniti na incidencijske strukture (primjer 3.1) i matrice (primjer 3.2) tako da im pridružimo grafove koji imaju izomorfne pune grupe automorfizama.

Incidencijskoj strukturi S = (P,L,I) pridružujemo bipartitni graf G(S) sa skupom vrhova V = P ČL (disjunktna unija). Točke su obojane bojom 1, a pravci bojom 2. Bridovi su { { P, l} | P Î P, l Î L, P I l }. Pokazuje se da je Aut(S) @ Aut(G(S)). Slično postupamo za matrice.

Međutim, u sklopu algoritma za klasifikaciju kojeg opisujemo u idućoj točki ipak ćemo koristiti algoritam 3.10. Treba nam kanonsko preslikavanje s nekim dodatnim svojstvima, koje za nauty ne možemo provjeriti. Za naše potrebe program canonmat je dovoljno brz.

Na kraju ovog odjeljka opisujemo jednu primjenu za koju možemo upotrijebiti bilo koje kanonsko preslikavanje, dakle i nauty. Radi se o problemu ``filtriranja''. Neka je S Í X skup objekata. Treba naći skup predstavnika za S, tj. P Í S sa svojstvima:

(1)

Svaki objekt iz S izomorfan je nekom iz P.

(2)

Objekti iz P međusobno su neizomorfni.

Problem se, na primjer javlja kod konstrukcije dizajna pomoću grupa automorfizama, kojom se bavimo u petom poglavlju. Dobivaju se skupovi dizajna među kojima može biti izomorfnih. Treba odrediti koliko ih ima do na izomorfizam i naći po jednog predstavnika iz svake klase.

Algoritam 16 [filter]
Na ulazu se nalaze objekti iz S. Objekti iz P ispisuju se na izlaz.

Prethodni algoritam realiziran je u programu incfilter . Program ``filtrira'' skupove 0-1 matrica. Za kanonsko preslikavanje koristi nauty. Skup T implementiran je kao stablo, da bi se upit C Î| T izvodio što brže.

3.2  Algoritam za klasifikaciju

Kao i dosad, X označava skup objekata na kojem djeluje grupa G. Pod klasifikacijom podrazumijevamo određivanje broja staza pri tom djelovanju i pronalaženje po jednog predstavnika iz svake staze.

Naivan pristup problemu klasifikacije bio bi generiranje pomoću računala svih objekata iz X i njihovo filtriranje algoritmom 3.16. To nije provedivo jer u praksi skup X ima previše elemenata. Na primjer, neka je X skup svih Steinerovih 2-dizajna S(3,13) na kojem djeluje grupa G = S₁₃ ×S₂₆. Do na izomorfizam postoje dva takva dizajna, S3.1 i S3.2. Korištenjem propozicije 1.18 možemo izračunati ukupan broj objekata u X:

Neka je zadana funkcija ord:X --> N. Kažemo da je objekt A reda ord(A). Skup svih objekata reda l označavamo X^(l) = { A Î X | ord(A) = l }. Algoritmom klasificiramo objekte reda m tako da prvo klasificiramo objekte manjeg reda l = 1,2,3,...

Neka na svakom nepraznom X^(l) djeluje grupa G^(l). Direktni produkt G = G⁽¹⁾ ×G⁽²⁾ ×... na prirodan način djeluje na X, (g₁,g₂,...)A = g_ord(A) A za A Î X i (g₁,g₂,...) Î G. U ovoj situaciji prirodno je definirati punu grupu automorfizama objekta A Î X^(l) kao njegov G^(l)-stabilizator, jer grupa G⁽¹⁾×...×G^(l-1) ×G^(l+1) ×... stabilizira sve objekte reda l.

Neka je c:X --> X kanonsko preslikavanje. Budući da izomorfni objekti imaju isti red, c čuva red objekata. Skup svih kanonskih objekata reda l označavamo C^(l) = { A Î X^(l) | c(A) = A }. Algoritmom konstruiramo C^(m), skup predstavnika za X^(m).

Najvažnija dodatna struktura na skupu X je veza između objekata različitog reda. Formalno, zahtjevamo postojanje funkcije p:X\X⁽¹⁾ --> X sa svojstvima:

(1)

p(X^(l+1)) Í X^(l), za svaki l (p smanjuje red objekata za jedan)

(2)

p(C^(l+1)) Í C^(l), za svaki l (p čuva kanonske objekte)

Primjer 17 Klasificiramo Steinerove 2-dizajne s parametrima v, b, r, k. Parcijalna incidencijska matrica je svaka matrica A = [a_ij] Î M_{l b}({0,1}) (1 Ł l Ł v) koja zadovoljava:

(1)

A·A^t = (r-1)I_l + J_l

(2)

ĺ_{i = 1}^l a_ij Ł k, za j = 1,...,b

Neka je X^(l) skup svih parcijalnih incidencijskih l×b matrica. Ako je l = v svojstva (1) i (2) povlače jednakost u (2), pa prema 1.9 skup X^(v) sadrži incidencijske matrice S(k,v) dizajna.

Neka je X = X⁽¹⁾Č...ČX^(v) i ord(A) = broj redaka matrice A. Na X^(l) djeluje grupa G^(l) = S_l ×S_b kao u primjeru 3.2. Za kanonsko preslikavanje uzmimo funkciju c(A) = max{ gA | g Î G }, pri čemu je G direktni produkt G⁽¹⁾ ×...×G^(b). Računamo ga pomoću algoritma 3.10, odnosno programa canonmat. Funkcija p neka je brisanje zadnjeg retka matrice,

Propozicija 18 Neka je A Î M_mn(N₀) kanonska matrica obzirom na funkciju c iz propozicije 3.6, tj. c(A) = A. Tada su i matrice A(1,...,i), i = 1,...,m kanonske, tj. c(A(1,...,i)) = A(1,...,i).

Dokaz. A(1,...,i) = c(A)(1,...,i) = (lema 3.11) =

Algoritam 19

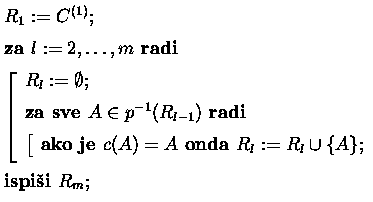
Propozicija 20 Nakon izvođenja algoritma 3.19 vrijedi R_l = C^(l), za l = 1,...,m.

Dokaz. Indukcijom po l. Za l = 1 tvrdnja vrijedi zbog inicijalizacije na početku algoritma. Pretpostavimo da je R_l-1 = C^(l-1). Nakon izvođenja l-tog koraka petlje očito je R_l = p^-1(R_l-1) ÇC^(l) = p^-1(C^(l-1)) ÇC^(l). Zbog svojstva (2) funkcije p vrijedi p^-1(C^(l-1)) Ę C^(l), pa je presjek jednak C^(l). Dakle, R_l = C^(l).

Algoritam realiziramo tako da se skupovi R₁,...,R_m pamte na vanjskoj memoriji računala (disku). Treba nam program za računanje praslike p^-1(R_l-1). U slučaju klasifikacije Steinerovih 2-dizajna proširujemo parcijalne incidencijske (l-1)×b matrice jednim retkom, do parcijalnih incidencijskih l×b matrica. Problem rješava program p-1, za proizvoljne parametre S(k,v). Treba nam još program koji iz niza objekata izbacuje one koji nisu kanonski. Za matrice nad N₀ koristimo program canonfilter, napisan na osnovu algoritma 3.10. Prilikom klasifikacije S(k,v) dizajna primjenjujemo ga na parcijalne incidencijske matrice.

Primjer 21 Klasificiramo Steinerove 2-dizajne S(3,13) algoritmom 3.19. Krećemo od jedinstvene parcijalne incidencijske 1×26 matrice u kanonskom obliku:

Programom p-1 proširujemo je do parcijalnih incidencijskih 2×26 matrica i pomoću canonfilter-a izbacujemo nekanonske. Tako dobivamo skup R₂ = C⁽²⁾, a analogno konstruiramo skupove R₃,...,R₁₃. Točan redoslijed pozivanja programa vidljiv je iz shell-skripte klas1. Rezultati su sabrani u tablici 5. Skup R₁₃ sadrži dvije incidencijske matrice, koje pripadaju dizajnima S3.1 i S3.2. Zaključujemo da do na izomorfizam postoje točno dva S(3,13) dizajna.

U primjeru vidimo glavni nedostatak algoritma 3.19. Skup R₁ proširivali smo do ukupno 93024 parcijalnih incidencijskih 2×26 matrica i zatim izbacivali nekanonske, a sasvim je jasno da je među njima samo jedna kanonska:

Štoviše, kanonske incidencijske matrice S(3,13) dizajna očito su oblika prikazanog na slici 5. Matrice koje nisu tog oblika ne treba ni razmatrati.

1 11111 00000 00000 000 000 0000
1 00000 11111 00000 000 000 0000
1 00000 00000 11111 000 000 0000

0 10000 10000 10000 111 000 0000
0 10000 01000 01000 000 111 0000

0 01000 1.... ..... ... ... ....
0 01000 0.... ..... ... ... ....

0 00100 0.... ..... ... ... ....
0 00100 0.... ..... ... ... ....

0 00010 0.... ..... ... ... ....
0 00010 0.... ..... ... ... ....

0 00001 0.... ..... ... ... ....
0 00001 0.... ..... ... ... ....

Općenito, neka je Y^(m) skup objekata reda m koji sadrži sve kanonske objekte (C^(m) Í Y^(m) Í X^(m)). Definiramo

Algoritam 22

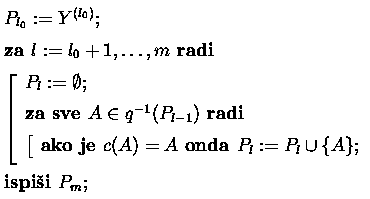
Propozicija 23 Nakon izvođenja algoritma 3.22 vrijedi P_m = C^(m).

Dokaz. Označimo Z^(m) = C^(m) i neka je Z^(l) = p(Z^(l+1)), za l = m-1, m-2,...,1. Silaznom indukcijom lako se pokazuje da za svaki l vrijedi C^(l) Ę Z^(l) i Y^(l) Ę Z^(l). Dokazujemo uzlaznom indukcijom da ista tvrdnja vrijedi za skupove definirane algoritmom, P_l Ę Z^(l) za l = l₀,...,m.

Zbog inicijalizacije na početku algoritma je P_l0 = Y^(l₀), pa tvrdnja vrijedi za l = l₀. Pretpostavimo P_l-1 Ę Z^(l-1). Iz toga slijedi p^-1(P_l-1) Ę p^-1(Z^(l-1)) Ę Z^(l). Algoritam definira skup P_l kao presjek

Primjer 24 Klasificiramo Steinerove 2-dizajne S(3,13) algoritmom 3.22. Neka je Y^(m) skup incidencijskih matrica za S(3,13) koje su oblika kao na slici 5. Među njima su sve kanonske incidencijske matrice. Skup Y^(l) sadrži parcijalne incidencijske matrice dobivene odbacivanjem v-l redaka matrica iz Y^(m). One su oblika kao prvih l redaka sa slike 5. Klasifikaciju započinjemo od jednočlanog skupa Y⁽⁵⁾, koji sadrži matricu:

Kod provedbe algoritma 3.22 jedina razlika u odnosu na algoritam 3.19 je što treba računati praslike q^-1(P_l-1) umjesto p^-1(R_l-1). Konkretno, to znači da (l-1)×b matrice proširujemo samo do l×b matrica iz skupa Y^(l), tj. do parcijalnih incidencijskih matrica oblika kao prvih l redaka sa slike 5. Koristimo program q-1 umjesto programa p-1. Točan redoslijed u kojem pozivamo programe vidljiv je iz shell-skripte klas2, a rezultati su sabrani u tablici 6.

Osnovni zahtjev koji postavljamo na algoritam za klasifikaciju je što manji broj objekata na koje primjenjujemo kanonsko preslikavanje. Vidimo da po tom kriteriju možemo spretnim odabirom skupa Y^(m) postići znatno poboljšanje algoritma 3.22 u odnosu na algoritam 3.19. U primjeru 3.21 ``filtrirali'' smo ukupno ĺ_{l = 1}¹² |p^-1(R_l)| = 186797 matrica, a u primjeru 3.24 samo ĺ_{l = 5}¹² |q^-1(P_l)| = 859.

Drugi problem koji se javlja prilikom klasifikacije je pohranjivanje međurezultata. U tipičnoj situaciji parcijalnih objekata ima znatno više nego potpunih, što je vidljivo i iz tablice 5. Kod klasifikacije S(3,13) dizajna skupovi R_l i P_l su zanemarivo mali i pohranjivanje ne predstavlja problem. Za veće dizajne skupovi mogu doseći kapacitet današnjih diskova čak i kad potpunih objekata nema puno. Vidimo da je i u tom pogledu algoritam 3.22 bolji od algoritma 3.19, jer ne pohranjuje sve parcijalne objekte. Na primjer, skup P₉ sadrži samo 10 od ukupno 33 parcijalnih incidencijskih 9×26 matrica.

Spomenimo da je B.D.McKay [15] razvio algoritam za klasifikaciju kod kojeg se ne pojavljuje taj problem. Ideja je klase ekvivalencije objekata organizirati u stablo, s potpunim objektima na posljednjem nivou. Stablo se pretražuje po dubini, za što je potrebno pamtiti samo po jedan objekt sa svakog nivoa. McKayev algoritam zahtjeva više strukture na skupu objekata X.

Primjer 25 Steinerove 2-dizajne S(3,15) klasificirali su 1983. godine R.Mathon, K.T.Phelps i A.Rosa (prema [4]). Dobili su ukupno 80 neizomorfnih dizajna. Ponavljamo klasifikaciju korištenjem algoritma 3.22 primjenjenog na incidencijske matrice oblika sa slike 6.

1 111111 000000 000000 0000 0000 00000000
1 000000 111111 000000 0000 0000 00000000
1 000000 000000 111111 0000 0000 00000000

0 100000 100000 100000 1111 0000 00000000
0 100000 010000 010000 0000 1111 00000000

0 010000 1..... ...... .... .... ........
0 010000 0..... ...... .... .... ........

0 001000 0..... ...... .... .... ........
0 001000 0..... ...... .... .... ........

0 000100 0..... ...... .... .... ........
0 000100 0..... ...... .... .... ........

0 000010 0..... ...... .... .... ........
0 000010 0..... ...... .... .... ........

0 000001 0..... ...... .... .... ........
0 000001 0..... ...... .... .... ........

Klasifikaciju započinjemo od skupa P₅ i programima q-1 i canonfilter konstruiramo skupove P₆,...,P₁₅. Kao što je vidljivo iz tablice 7, također dobivamo 80 dizajna S(3,15).

Primjer 26 Steinerove 2-dizajne S(4,25) klasificirao je E.Spence [18] 1996. godine. Spence je algoritmom 3.22 konstruirao parcijalne incidencijske 13×50 matrice oblika sa slike 7.

1 1111111 0000000 0000000 0000000 0000 0000 0000 000000000
1 0000000 1111111 0000000 0000000 0000 0000 0000 000000000
1 0000000 0000000 1111111 0000000 0000 0000 0000 000000000
1 0000000 0000000 0000000 1111111 0000 0000 0000 000000000

0 1000000 1000000 1000000 1000000 1111 0000 0000 000000000
0 1000000 0100000 0100000 0100000 0000 1111 0000 000000000
0 1000000 0010000 0010000 0010000 0000 0000 1111 000000000

0 0100000 1...... ....... ....... .... .... .... .........
0 0100000 0...... ....... ....... .... .... .... .........
0 0100000 0...... ....... ....... .... .... .... .........

0 0010000 1...... ....... ....... .... .... .... .........
0 0010000 0...... ....... ....... .... .... .... .........
0 0010000 0...... ....... ....... .... .... .... .........

0 0001000 0...... ....... ....... .... .... .... .........
0 0001000 0...... ....... ....... .... .... .... .........
0 0001000 0...... ....... ....... .... .... .... .........

0 0000100 0...... ....... ....... .... .... .... .........
0 0000100 0...... ....... ....... .... .... .... .........
0 0000100 0...... ....... ....... .... .... .... .........

0 0000010 0...... ....... ....... .... .... .... .........
0 0000010 0...... ....... ....... .... .... .... .........
0 0000010 0...... ....... ....... .... .... .... .........

0 0000001 0...... ....... ....... .... .... .... .........
0 0000001 0...... ....... ....... .... .... .... .........
0 0000001 0...... ....... ....... .... .... .... .........

Dobio je 120014 kanonskih matrica. U nastavku klasifikacije više se ne isplati izbacivati nekanonske matrice nakon proširivanja jednim retkom, nego tek kad ih proširimo do potpunih incidencijskih matrica. Za konstrukciju skupa P₁₄ trebalo bi filtrirati znatno više matrica nego što ih dobivamo proširivanjem matrica iz P₁₃ do kraja. Spence je na taj način dobio 18 neizomorfnih S(4,25) dizajna.

Ovdje klasifikaciju ponavljamo samo djelomično. Pomoću programa q-1 i canonfilter konstruiramo skupove P₇,...,P₁₁ (tablica 8). Spence je za računanje kanonskih predstavnika koristio program F.Bussemakera, koji je osjetno brži od programa canonmat. Postupak proširivanja matrica iz P₁₃ do potpunih incidencijskih matrica također je vrlo dugotrajan. Spenceovi programi trebali su više mjeseci procesorskog vremena.

Vidimo da su algoritmom 3.22 klasificirani dizajni S(3,13), S(3,15) i S(4,25). Izuzevši projektivne i afine ravnine, to su jedini parametri za koje je poznat točan broj Steinerovih 2-dizajna. Projektivne i afine ravnine, S(n+1,n²+n+1) i S(n,n²) klasificirane su pomoću računala sve do n = 10. Korišene su veze s latinskim kvadratima (za n Ł 9) i binarnim kodovima (za n = 10). Više o tome može se pročitati u diplomskom radu [10].

Primjer 27 Na kraju objašnjavamo primjenu algoritma za klasifikaciju na orbitne strukture. Neka su zadani vektori n = (n₁,...,n_m) Î N^m i b = (b₁,...,b_n) Î Nⁿ (zovemo ih marginalni vektori). Označimo v = ĺ_{i = 1}^mn_i, b = ĺ_{j = 1}ⁿ b_j i neka su r,k,l Î N. Orbitna struktura je svaka matrica A = [ a_ij ] Î M_mn(N₀) koja zadovoljava:

(1)

0 Ł a_ij Ł b_j, za 1 Ł i Ł m, 1 Ł j Ł n

(2)

ĺ_{j = 1}ⁿ a_ij = r, za 1 Ł i Ł m

(3)

ĺ_{i = 1}^m (n_i/b_j) a_ij = k, za 1 Ł j Ł n

(4)

n ĺ j = 1  (ni / bj) aij ai˘j = ě ď í ď î lni, ako je i =|= i˘ l(ni-1)+r, ako je i = i˘ , za 1 Ł i,i˘ Ł m

Takve matrice javljaju se prilikom konstrukcije (v,k,l) blok dizajna sa zadanom grupom automorfizama (vidi poglavlje 5.1). Pretpostavljamo da su parametri v, b, r, k, l dopustivi.

Parcijalna orbitna struktura je matrica A = [a_ij] Î M_ln(N₀), 1 Ł l Ł m, koja ima svojstva (1), (2), (4) i

(3˘)

ĺ_{i = 1}^l (n_i/b_j) a_ij Ł k, za 1 Ł j Ł n

Neka je X skup svih parcijalnih orbitnih struktura. Red ord(A) je broj redaka matrice A, pa je X^(l) skup parcijalnih l×n orbitnih struktura. Matrice u X^(m) su orbitne strukture, jer uvjeti (2) i (3˘) zajedno s l = m impliciraju uvjet (3). Računamo:

Pri definiciji izomorfizma (parcijalnih) orbitnih stuktura treba paziti da svojstva (1) - (4) ostanu sačuvana. Dopuštamo samo permutacije redaka i stupaca koje ostavljaju marginalne vektore invarijantnim:

Kao i prije, definiramo G = G⁽¹⁾ ×...×G^(m). Za kanonsko preslikavanje uzimamo funkciju c(A) = max{ (p,s)A | (p,s) Î G }, obzirom na uređaj među matricama definiran u 3.7. Uz male modifikacije funkciju c možemo računati algoritmom 3.10, odnosno programom canonmat.

Veza među matricama različitog reda neka je brisanje zadnjeg retka:

Ako imamo informaciju o obliku kanonskih orbitnih struktura možemo dodatno ubrzati klasifikaciju korištenjem algoritma 3.22. Računanje praslike q^-1(P_l-1) je proširivanje parcijalnih orbitnih struktura jednim retkom, na sve dozvoljene načine. Treba poštivati zadani oblik, a proširene matrice također trebaju biti parcijalne orbitne strukture. Zadatak rješava program t-1.

Proširene matrice nisu sve u kanonskom obliku, pa ih treba ``filtrirati''. To radimo programom canonfilter s opcijom -t. Navođenjem opcije razmatraju se samo permutacije redaka i stupaca koje ostavljaju marginalne vektore invarijantnim. Klasifikacija orbitnih struktura bit će ilustrirana nizom konkretnih primjera u petom poglavlju.

4  Konstrukcija pomoću diferencijskih familija

4.1  Diferencijske familije

U ovom poglavlju G označava konačnu grupu reda v. Binarnu operaciju zapisujemo aditivno, iako G ne mora biti Abelova.

Definicija 1 Neka grupa (G,+) djeluje na skup X. Kažemo da je djelovanje regularno ako za bilo koje x,y Î X postoji jedinstveni g Î G takav da je g+x = y.

Regularno djelovanje omogućuje identifikaciju elemenata skupa X s elementima grupe G. Odaberemo čvrsti x₀ Î X i definiramo funkciju j: X --> G, j(x) = jedinstveni g Î G sa svojstvom g + x₀ = x. Zbog regularnosti j je dobro definirana bijekcija. Uz identifikaciju x ş j(x) djelovanje se podudara s lijevim translacijama u grupi G. Obrnuto, djelovanje bilo koje grupe na samu sebe lijevim translacijama je regularno.

Definicija 2 Neka je F = { D₁,..., D_n } familija k-članih podskupova od G. Razvoj familije F je incidencijska struktura dev F = (G, G+F, Î ), pri čemu je G + F = { g+D_i | g Î G, i = 1,...,n }, g+D_i = { g+x | x Î D_i }. Elemente iz F zovemo temeljni blokovi razvoja dev F.

Razvoj familije F je uniformna incidencijska struktura, tj. svaki blok sadrži točno k točaka. Ukoliko F sadrži dva bloka koji pripadaju istoj G-orbiti, recimo D₁ = g+D₂ za neki g Î G, tada je dev {D₁,D₂,...,D_n} = dev {D₂,..., D_n}. Stoga možemo pretpostaviti da temeljni blokovi pripadaju različitim stazama pri djelovanju G na P_k(G).

Propozicija 3 G je grupa automorfizama incidencijske strukture dev F, koja djeluje regularno na točke.

Dokaz. G djeluje na točke i pravce od dev F lijevim translacijama. Očito vrijedi x Î y+D_i Ű g+x Î g+y+D_i, pa je G grupa automorfizama. Djelovanje na točke je regularno jer se radi o lijevim translacijama u G.

Definicija 4 Multiskup m na G je funkcija m:G --> N₀. Kažemo da je element g Î G sadržan m(g) puta u m. Lista u G je funkcija l:S --> G, pri čemu je S konačan skup.

Poseban slučaj liste je uređena n-torka (konačan niz) s elementima iz G. (g₁,...,g_n) je funkcija g:{1,...,n} --> G, g(i) = g_i. Svaka lista na prirodan način definira multiskup: m(g) = | l^-1(g) |, za g Î G. Svaki multiskup možemo definirati listom, ali ne jedinstvenom.

Definicija 5 Neka je D Í G podskup grupe G. Lista razlika skupa D je funkcija

Da bi definirali listu i multiskup razlika za familiju podskupova od G treba nam pojam unije lista, odnosno multiskupova.

Definicija 6 Unija multiskupova je njihov zbroj, m₁ Č...Čm_n = m₁+...+m_n. Disjunktna unija skupova S₁,...,S_n je skup

Iz definicije slijedi da je multiskup pridružen uniji lista jednak uniji multiskupova pridruženih tim listama.

Definicija 7 Lista razlika familije F = {D₁,...,D_n} podskupova od G je unija njihovih lista razlika, DF = DD₁ Č...ČDD_n. Pripadni multiskup također označavamo DF.

Teorem 8 Neka je F = {D₁,...,D_n} familija k-članih podskupova grupe G koji imaju trivijalne stabilizatore i pripadaju različitim stazama pri djelovanju G na P_k(G). Tada je ekvivalentno:

(1)

Multiskup razlika DF sadrži svaki element iz G\{0} točno l puta.

(2)

Razvoj devF je (v,k,l) blok dizajn.

Dokaz. Neka je zadan dvočlani podskup {a,b} Í G. Dokazat ćemo da je broj blokova od dev
F koji ga sadrže jednak broju pojavljivanja elementa (-a)+b u multiskupu DF. Iz toga će slijediti tvrdnja teorema.

Blokove razvoja dev F možemo identificirati sa skupom

Definicija 9 Neka F zadovoljava pretpostavke teorema 4.8 i bilo koju od ekvivalentnih tvrdnji (1), (2). Tada F zovemo (v,k,l) diferencijska familija.

Propozicija 10 Ako postoji (v,k,l) diferencijska familija, onda je l(v-1) ş 0 (mod k(k-1)).

Dokaz. Neka je F = { D₁,...,D_n} (v,k,l) diferencijska familija. Domena liste razlika DF ima nk(k-1) elemenata. Razlike pokrivaju skup G\{0} točno l puta, pa je taj broj jednak l·|G\{0}| = l(v-1).

Korolar 11 Ako je F = {D₁,...,D_n} (v,k,1) diferencijska familija, onda je v = nk²-nk+1.

Vidimo da Steinerovi 2-dizajni konstruirani pomoću (v,k,1) diferencijskih familija imaju parametre oblika S(k,nk²-nk+1) i dopuštaju grupu automorfizama regularnu na točkama. Sljedeći cilj je dokazati obrat: ako Steinerov 2-dizajn S(k,nk²-nk+1) ima grupu automorfizama regularnu na točkama, može se konstruirati pomoću diferencijske familije.

Lema 12 Neka Steinerov 2-dizajn S(k,nk²-nk+1) ima grupu automorfizama G regularnu na točkama. Tada su G-stabilizatori pravaca trivijalni.

Dokaz. Pretpostavimo suprotno, da postoji pravac l = {T₁,...,T_k} invarijantan obzirom na netrivijalni automorfizam a Î G. Možemo pretpostaviti da je a prostog reda p. U suprotnom, ako je a reda p·r za r > 1, zamijenimo ga s a^r. Zbog regularnosti a nema fiksnih točaka, pa iz a({T₁,...,T_k}) = {T₁,...,T_k} slijedi p | k. No p dijeli i v = |G|, što je kontradikcija jer su k i v = nk²-nk+1 relativno prosti.

Propozicija 13 Neka Steinerov 2-dizajn S s parametrima S(k,nk²-nk+1) ima grupu automorfizama G regularnu na točkama. Tada postoji diferencijska familija F u G takva da je devF @ S.

Dokaz. Zbog regularnosti možemo identificirati točke s automorfizmima. To znači da je G skup točaka od S, a pravci su neki k-člani podskupovi od G. Broj pravaca je

Napomena 14 Uvjet da su parametri oblika S(k,nk²-nk+1) je nuždan, kao što pokazuje sljedeći primjer. Neka je G = Z₁₅ i F = { {0,1,4}, {0,2,9}, {0,5,10}}. Razvoj dev F je Steinerov 2-dizajn S(3,15). On prema propoziciji 4.3 ima Z₁₅ kao grupu automorfizama koja djeluje regularno na točke. Međutim, v = 15 nije oblika nk²-nk+1 = 6n+1, pa se dev F ne može konstruirati pomoću diferencijske familije (korolar 4.11). Zaista, temeljni blok {0,5,10} ima netrivijalni stabilizator, a 5 i 10 mogu se na više načina prikazati kao razlike (DF sadrži svakog po tri puta). Stoga F nije diferencijska familija, prema definiciji 4.9. Ponekad se u definiciji diferencijske familije dozvoljavaju blokovi s netrivijalnim stabilizatorom, koji se nazivaju kratki blokovi.

Steinerovi 2-dizajni koje proučavamo u ovom radu imaju parametre oblika S(k,2k²-2k+1), prikladne za konstrukciju pomoću diferencijskih familija s dva temeljna bloka (n = 2).

Teorem 15 Steinerovi 2-dizajni S(k,2k²-2k+1) s grupom automorfizama regularnom na točkama postoje i jedinstveni su za k = 3,4,5, a ne postoje za k = 6,7,8.

Dokaz. Za k = 3 postoje dva dizajna S(3,13). Dizajn S3.1 ima Z₁₃ kao regularnu grupu automorfizama. Puna grupa automorfizama dizajna S3.2 ne djeluje tranzitivno, pa ne može imati regularnu podgrupu (vidi tablicu 1).

Za k = 4 postoji osamnaest dizajna S(4,25). Od toga jedino dizajn S4.2 ima punu grupu automorfizama tranzitivnu na točkama. Ona ima podgrupu koja djeluje regularno, izomorfnu sa Z₅ ×Z₅. Ostali S(4,25) dizajni ne mogu se konstruirati pomoću diferencijske familije.

Za k = 5 dizajni S(5,41) nisu potpuno klasificirani. Od poznatih primjera jedino S5.1 dopušta grupu automorfizama regularnu na točkama. To dokazuje samo egzistenciju, pa treba još dokazati jedinstvenost za k = 5 i nepostojanje za k = 6,7,8.

Primijetimo najprije da su grupe reda 41, 61, 85 i 113 jedinstvene. Radi se naravno o cikličkim grupama. Problem rješavamo računalom, pomoću programa dfsearch koji sustavno traži diferencijske familije u cikličkim grupama. U grupi Z₄₁ dobivamo nekoliko diferencijskih familija s n = 2, čiji su razvoji izomorfni dizajnu S5.1. Zaključujemo da je to jedini S(5,41) dizajn s regularnom grupom automorfizama. U grupama Z₆₁, Z₈₅ i Z₁₁₃ program ne nalazi diferencijske familije s n = 2. Prema tome, ne postoje dizajni S(6,61), S(7,85) i S(8,113) s regularnim grupama automorfizama.

Napomena 16 Potraga za (113,8,1) diferencijskim familijama trajala je na računalima koja su mi bila dostupna oko tjedan dana. Njihovo nepostojanje je nov rezultat.

4.2  Wilsonov teorem

Vidjeli smo da su poznata tri Steinerova 2-dizajna S(k,2k²-2k+1) koje je moguće konstruirati pomoću diferencijske familije. Egzistencija pripadnih diferencijskih familija slijedi iz teorema R.M.Wilsona [21]. U tom teoremu ulogu grupe G igra zbrajanje u konačnom polju. Osnovna svojstva konačnih polja sabrana su u sljedećem teoremu.

Teorem 17

(1)

Konačno polje s q elemenata postoji ako i samo ako je q prim potencija. Ako postoji, jedinstveno je do na izomorfizam i označavamo ga s GF(q).

(2)

Aditivna grupa polja GF(q) je elementarno Abelova, reda q. Multiplikativna grupa je ciklička, reda q-1. Svaki generator multiplikativne grupe nazivamo primitivni element polja GF(q).

(3)

Ako je q-1 = m·n, multiplikativna grupa ima jedinstvenu podgrupu reda n i indeksa m, koju označavamo H^m. Radi se o n-tim korijenima jedinice, odnosno m-tim potencijama ne-nul elemenata:

Hm = { x Î GF(q) | xn = 1 } = { xm | x Î GF(q)\{0} }.

(4)

Ako je q paran, -1 = 1 pa sve podgrupe H^m sadrže -1. Ako je q neparan, -1 Î H^m ako i samo ako je n = (q-1)/m paran.

Definicija 18 Ako liste l₁ : S --> G i l₂ : T --> G definiraju isti multiskup na G kažemo da su ekvivalentne i pišemo l₁ ş l₂.

Lema 19 Liste l₁ : S --> G, l₂ : T --> G su ekvivalentne ako i samo ako postoji bijekcija j: T --> S sa svojstvom l₂ = l₁ °j.

Dokaz. (Ţ) Za svaki g Î G skupovi S_g = l₁^-1(g) i T_g = l₂^-1(g) su jednakobrojni, pa postoji bijekcija j_g : T_g --> S_g. Traženu bijekciju j: T --> S dobivamo proširivanjem, j(x) = j_l2(x)(x).

(Ü) Iz l₂ = l₁ °j slijedi l₂^-1(g) = (l₁ °j)^-1(g) = j^-1(l₁^-1(g)). Zbog bijektivnosti od j to povlači |l₂^-1(g)| = |l₁^-1(g)|, za svaki g Î G.

Definicija 20 Produkt lista l₁ : S --> GF(q) i l₂ : T --> GF(q) je lista l₁ ·l₂ : S×T --> GF(q), (l₁ ·l₂)(x,y) = l₁(x) ·l₂(y).

Lema 21 Množenje lista u GF(q) je do na ekvivalenciju distributivno obzirom na uniju,
(l₁ Č l₂) ·l₃ ş (l₁ ·l₃) Č(l₂ ·l₃).

Dokaz. Ako domenu od l_i označimo sa S_i, domena liste (l₁ Čl₂) ·l₃ je

Teorem 22 [Wilson, 1972.] Neka je q = nk²-nk+1 prim potencija, a w primitivni element konačnog polja GF(q).

(1)

Ukoliko je k = 2m+1 neparan, neka je e = w^2mn i D = {1,e,...,e^k-1}. Ako elementi e-1, e²-1,...,e^m-1 pripadaju različitim klasama modulo H^m, onda je F = { D,w^m D,...,w^(n-1)m D} (q,k,1) diferencijska familija.

(2)

Ukoliko je k = 2m paran, neka je e = w^2mn i D = {0,1,e,...,e^k-2}. Ako elementi 1,e-1,...,e^m-1-1 pripadaju različitim klasama modulo H^m, onda je F = { D,w^m D,...,w^(n-1)m D} (q,k,1) diferencijska familija.

Dokaz. (1) Prvo dokazujemo teorem za neparni k. U tom slučaju e je primitivni k-ti korijen jedinice, tj. generator podgrupe D = H^2mn. Vidjet ćemo da multiskup DF sadrži svaki ne-nul element točno jednom. Iz toga slijedi da temeljni blokovi leže u različitim stazama i imaju trivijalne stabilizatore obzirom na djelovanje aditivne grupe. Kad bi dva temeljna bloka pripadala istoj orbiti, pripadne liste razlika bile bi jednake pa bi DF neke elemente sadržao bar dva puta. Nadalje, kad bi za neki a =|= 0 vrijedilo a+ w^imD = w^imD, taj bi se a na više načina mogao prikazati kao razlika elemenata iz w^imD.

Preostaje dokazati da DF pokriva GF(q)\{0} točno jednom. Dokaz se sastoji od tri koraka.

Korak 1. DD ş +-D ·(e-1,e²-1,...,e^m-1)

Na lijevoj strani je lista razlika skupa D. To je funkcija

Korak 2. +-D = H^mn

Znamo da je D = H^2mn podgrupa reda k. Skup +-D je zatvoren obzirom na množenje i invertiranje, pa je i to podgrupa. Ona je reda 2k, jer su D i -D disjunktni. Zbog jedinstvenosti u teoremu 4.17(3) +-D se podudara s H^mn.

Korak 3. DF ş H^m ·(e-1,e²-1,...,e^m-1)

U prva dva koraka dokazali smo DD ş H^mn ·(e-1,...,e^m-1). Lako se provjeri D(w^imD) ş w^imDD, pa slijedi

Time je i treći korak dokazan. Ako e-1,...,e^m-1 pripadaju različitim klasama modulo H^m, skupovi H^m(e-1),...,H^m(e^m-1) su međusobno disjunktni. Zajedno s tvrdnjom trećeg koraka to povlači DF ş GF(q)\{0}.

(2) Za parni k dokaz je sličan. e je primitivni (k-1)-vi korijen jedinice (generator od H^2mn), a D = {0} ČH^2mn. Temeljni blokovi pripadaju različitim stazama i imaju trivijalne stabilizatore. To slijedi iz DF ş GF(q)\{0}, što ponovo dokazujemo u tri koraka.

Korak 1. DD ş +-H^2mn ·(1,e-1,...,e^m-1-1)

Korak 2. +-H^2mn = H^mn

Korak 3. DF ş H^m ·(1,e-1,...,e^m-1-1)

Dokazi ovih triju tvrdnji analogni su dokazima iz slučaja (1), pa ih nećemo ponavljati.

Propozicija 23 Steinerov 2-dizajn konstruiran pomoću teorema 4.22 ima kao grupu automorfizama semidirektan produkt grupe H^2mn s aditivnom grupom od GF(q), pri čemu H^2mn djeluje množenjem na GF(q).

Dokaz. Neka je G = H^2mn ×GF(q). Operaciju u G definiramo s

Primjer 24 Nas prvenstveno zanima primjena teorema za n = 2, jer tako dobivamo Steinerove 2-dizajne S(k,2k²-2k+1). Pogledajmo najprije slučaj k = 3, u kojem je q = 13 primbroj. Konačno polje GF(13) čine cijeli brojevi sa zbrajanjem i množenjem modulo 13, (Z₁₃,+₁₃,·₁₃). Za primitivni element možemo uzeti w = 2. k je neparan, m = 1, e = w^2mn = 3 i D = {1,3,9}. Skup elemenata za koje treba provjeriti da leže u različitim klasama modulo H^m je jednočlan, pa je uvjet ispunjen. Prema teoremu 4.22 F₃ = {D, wD} = { {1,3,9}, {2,6,5}} je (13,3,1) diferencijska familija. Razvoj dev F₃ izomorfan je sa S3.1 i prema 4.23 ima grupu automorfizama Z₃.Z₁₃. To je ujedno puna grupa automorfizama.

Primjer 25 Za n = 2, k = 4 dobivamo prim potenciju q = 25. Konačno polje GF(25) konstruiramo kao kvocijent Z₅[x] / (x²+2) prstena polinoma nad Z₅. Polinom x²+2 je ireducibilan, pa je ideal (x²+2) maksimalan. To znači da je kvocijentni prsten polje, koje očito ima 25 elemenata. Kao primitivni element w uzmimo polinom x+1. U ovom slučaju k je paran, m = 2, e = w^2mn = (x+1)⁸ ş x+2 (mod x²+2) i D = {0,1,x+2,4x+2}. Treba provjeriti da 1 i e-1 = x+1 leže u različitim klasama modulo H² = áw² ń. To vrijedi jer je 1 Î H², a e-1 = w Î| H². Wilsonov teorem nam daje (25,4,1) diferencijsku familiju F₄ = { D, w² D} = {{0,1,x+2,4x+2}, {0,2x+4,3x+4,2}}. Razvoj dev F₄ izomorfan je sa S4.2. Na njemu prema 4.23 djeluje G = Z₃ . (Z₅ ×Z₅), ali to nije puna grupa automorfizama. Involucija ax +b --> -ax + b ostavlja temeljne blokove invarijantnim. Zato je ona također automorfizam, koji s G tvori semidirektan produkt. Tako dobivamo punu grupu automorfizama od dev F₄, Z₂ . G.

Primjer 26 Za n = 2 i k = 5 dobivamo primbroj q = 41. w = 6 je primitivni element polja GF(41) = (Z₄₁,+₄₁,·₄₁). k je neparan, m = 2, e = 10 i D = {1,10,18,16,37}. Brojevi e-1 = 9 i e²-1 = 17 leže u različitim klasama modulo H² jer 9 jest, a 17 nije dvadeseti korijen jedinice (tj. 9 Î H², 17 Î| H²). Zato je F₅ = {D,w² D} = {{1,10,18,16,37}, {36,32,33,2,20}} (41,5,1) diferencijska familija u Z₄₁. Razvoj dev F₅ je izomorfan sa S5.1, a propozicija 4.23 ponovo daje punu grupu automorfizama Z₅ . Z₄₁.

Definicija 27 Neka je q = nk²-nk+1 prim potencija. Za (q,k,1) diferencijsku familiju u GF(q) kažemo da je radikalna ako:
- za neparni k, temeljni blokovi su klase modulo H^(k-1)n
- za parni k, temeljni blokovi su unije klasa modulo H^kn s nulom.
`Radikalna diferencijska familija' kratko pišemo RDF.

Teorem 4.22 daje dovoljan uvjet za postojanje radikalne diferencijske familije. Ako za neparni k elementi e-1,...,e^m-1, a za parni 1,e-1,...,e^m-1-1 pripadaju različitim klasama modulo H^m, onda je F = { w^imD | i = 0,...,n-1 } RDF.

Uvjet teorema nije nuždan. Neka je k = 2m = 4, n = 16, q = 193. Primitivni element polja GF(193) je w = 5. Označimo e = w^2mn = 84, D = {0} ČH^kn = {0,1,84,108}. Budući da 1 i e-1 = 83 oba leže u H^m, familija F = { w²ⁱD | i = 0,...,15 } iz 4.22 nije diferencijska. Međutim, u GF(193) ipak postoji RDF: F˘ = { w^i+4jD | i = 0,1, j = 0,...,7 }.

M. Buratti je u [3] dao slabiji uvjet za postojanje radikalne diferencijske familije. Uz oznake teorema 4.22, kvocijente iz skupa A Í GF(q)\{0} označimo F(A) = { xy^-1 | x,y Î A }. Neka postoji niz djelitelja d₀ = 1 | d₂ | d₃ | ...| d_2s+1 = mn takav da:

(1)

n = Ő_{i = 0}^s d_2i+1 / d_2i

(2)

Za neparni k skup F(e-1,...,e^m-1), a za parni F(1,e-1,...,e^m-1-1) sadržan je u

s Č i = 1  ( Hd2i+1 \Hd2i ) Č {1}

Tada je F˘ = { wⁱ D | i Î I },

Wilsonov uvjet implicira Burattijev, a ako su m i n relativno prosti s njim je ekvivalentan. Burattijev uvjet je i nuždan za k Ł 7. Radikalna diferencijska familija u GF(193) dobivena je pomoću niza djelitelja 1 | 2 | 4 | 8 | 8 | 16 | 16 | 32.

U sljedećoj propoziciji dan je jedan nuždan uvjet za postojanje RDF.

Propozicija 28 Neka je q = nk²-nk+1 prim potencija, w primitivni element u GF(q), m = [^k/₂], e = w^2mn. Ako postoji radikalna (q,k,1) diferencijska familija, onda za neparni k elementi e-1,...,e^m-1, a za parni 1,e-1,...,e^m-1-1 leže u različitim klasama modulo H^mn.

Dokaz. Neka je k = 2m+1 neparan. Uvjet da e-1,...,e^m-1 pripadaju različitim klasama modulo H^mn ne ovisi o izboru primitivnog elementa w, iako je e = w^2mn definiran pomoću njega. Naime, vrijedi

U dokazu teorema 4.22 vidjeli smo da je D(aH^2mn) ş aH^mn ·(e-1,...,e^m-1). Ako dva elementa među e-1,...,e^m-1 pripadaju istoj klasi modulo H^mn, multiskupovi razlika klasa aH^2mn sadrže neke elemente dva ili više puta. Tada klase ne mogu biti temeljni blokovi diferencijske familije.

Dokaz je za parni k sličan.

Pomoću propozicije 4.28 možemo ustanoviti nepostojanje radikalnih diferencijskih familija. Zanima nas slučaj n = 2; promotrimo u kojim je od polja GF(q), q = 2k²-2k+1 ispunjen nužni uvjet. Za k = 3,4,5,6,8,10 elementi e-1,...,e^m-1, odnosno 1,e-1,...,e^m-1-1 pripadaju različitim klasama modulo H^mn. Znamo da RDF postoje za k = 3,4,5. Za k = 6,8,10 liste razlika skupova oblika {0} ČaH^2mn imaju u parovima neprazne presjeke, pa ne mogu tvoriti diferencijske familije. Nužni uvjet nije zadovoljen za 11 Ł k Ł 2000, kad god je q = 2k²-2k+1 prim potencija. To sam provjerio pomoću sustava za računalnu algebru Mathematica (Wilson.nb). Time je dokazan sljedeći rezultat.

Propozicija 29 Radikalne (2k²-2k+1,k,1) diferencijske familije postoje za k = 3,4,5, a ne postoje za 6 Ł k Ł 2000.

5  Konstrukcija pomoću grupa automorfizama

5.1  Metoda konstrukcije

U ovom poglavlju koristimo poznatu metodu za konstrukciju blok dizajna sa zadanim parametrima i grupom automorfizama. Metodu je među prvima uspješno upotrebljavao hrvatski matematičar Z.Janko, pa je kod nas poznata kao ``Jankova metoda''. Centralnu ulogu igra pojam taktičke dekompozicije.

Definicija 1 Neka je (P,L,I) incidencijska struktura. Taktička dekompozicija sastoji se od particije skupa točaka

(1)

Broj točaka iz P_i incidentnih s pravcem l Î L_j ne ovisi o izboru tog pravca.

(2)

Broj pravaca iz L_j incidentnih s točkom T Î P_i ne ovisi o izboru te točke.

Propozicija 2 Neka je G grupa automorfizama incidencijske strukture. Particija skupa točaka i pravaca na G-orbite čini taktičku dekompoziciju.

Dokaz. Neka su l, l˘ pravci iz iste G-orbite L_j, tj. l˘ = g l za neki g Î G. Neka je P_i orbita na točkama. Djelovanje grupe G na točke i pravce čuva incidenciju. Stoga je T --> gT bijekcija između skupa točaka iz P_i incidentnih s l, odnosno l˘. Svojstvo (2) dokazuje se analogno.

Taktička dekompozicija dizajna ima dodatne pravilnosti. Neka je (P,L,I) blok dizajn s parametrima v, b, r, k, l, a

Označimo nadalje

Lema 3

Dokaz. ĺ_{j = 1}ⁿ a_ij = ĺ_{j = 1}ⁿ | { l Î L_j | T I l }| = |{ l Î L | T I l }| = r. Druga tvrdnja dokazuje se analogno.

Lema 4 Za svaki 1 Ł i Ł m, 1 Ł j Ł n vrijedi n_i a_ij = b_j b_ij.

Dokaz. Dvostrukim prebrojavanjem incidentnih parova iz P_i ×L_j.

Lema 5 Za sve 1 Ł i, i˘ Ł m vrijedi

Dokaz. Neka je T Î P_i˘ bilo koja točka. Skup svih pravaca koji prolaze kroz T označavamo (T). Računamo:

Ako je i =|= i˘ točke P i T pripadaju različitim blokovima particije, pa su različite. Tada ih spaja točno l pravaca, tj. |(T)Ç(P)| = l. Vidimo da je u ovom slučaju ĺ_{j = 1}ⁿ a_i˘j b_ij = ĺ_{P Î Pi}l = ln_i.

Ako je i = i˘ točke P i T mogu biti jednake. Vrijedi

Propozicija 6 Matrica A = [a_ij] ima svojstva:

(1)

0 Ł a_ij Ł b_j, za 1 Ł i Ł m, 1 Ł j Ł n

(2)

ĺ_{j = 1}ⁿ a_ij = r, za 1 Ł i Ł m

(3)

ĺ_{i = 1}^m (n_i / b_j) a_ij = k, za 1 Ł j Ł n

(4)

n ĺ j = 1  (ni / bj) aij ai˘j = ě ď í ď î lni, ako je i =|= i˘ l(ni-1)+r, ako je i = i˘ , za 1 Ł i,i˘ Ł m

Dokaz. Svojstvo (1) slijedi direktno iz definicije brojeva a_ij, a svojstvo (2) dokazali smo u lemi 5.3. Svojstvo (3) slijedi iz lema 5.3 i 5.4, a svojstvo (4) iz lema 5.4 i 5.5.

Slično dokazujemo svojstva matrice B.

Propozicija 7 Matrica B = [b_ij] ima svojstva:

(1)

0 Ł b_ij Ł n_i, za 1 Ł i Ł m, 1 Ł j Ł n

(2)

ĺ_{i = 1}^m b_ij = k, za 1 Ł j Ł n

(3)

ĺ_{j = 1}ⁿ (b_j / n_i) b_ij = r, za 1 Ł i Ł m

(4)

n ĺ j = 1  (bj / ni˘) bij bi˘j = ě ď í ď î lni, ako je i =|= i˘ l(ni-1)+r, ako je i = i˘ , za 1 Ł i,i˘ Ł m

Definicija 8 Svaku matricu A = [a_ij] Î M_mn(N₀) koja ima svojstva iz propozicije 5.6 zovemo orbitna struktura (ili matrica taktičke dekompozicije) (v,k,l) dizajna obzirom na marginalne vektore n, b.

Napomena 9 Točnije bi bilo matricu A zvati točkovna orbitna struktura, a matricu B pravčasta orbitna struktura. U ovom radu za konstrukciju dizajna koristimo isključivo točkovne orbitne strukture.

Postupak za konstrukciju (v,k,l) dizajna s grupom automorfizama G sastoji se od dva koraka.

1. Pronalaženje svih orbitnih struktura, do na izomorfizam. Izomorfizam orbitnih struktura je permutacija redaka i stupaca koja čuva marginalne vektore. Koristimo algoritam za klasifikaciju, kao što je opisano u 3.27.

2. Indeksiranje orbitnih struktura. Unose u orbitnoj strukturi zamjenjujemo na sve moguće načine odgovarajućim 0-1 matricama, tako da dobijemo incidencijsku matricu (v,k,l) dizajna. Unos a_ij zamjenjujemo 0-1 matricom dimenzije n_i ×b_j. Matrica ima a_ij jedinica u svakom retku i invarijantna je obzirom na djelovanje grupe G.

Ako postupak indeksiranja primjenimo na sve orbitne strukture dobit ćemo incidencijske matrice svih (v,k,l) dizajna s grupom automorfizama G.

Treba naglasiti da osim strukture grupe G moramo znati način na koji ona djeluje na točke i pravce dizajna. Najteži dio posla upravo je odabir prikladne grupe i konzistentnog djelovanja. U ovom radu bavimo se isključivo konstrukcijom S(k,2k²-2k+1) dizajna s cikličkim grupama prostog reda Z_p. U tom slučaju orbite su duljine 1 ili p, jer Z_p nema pravih podgrupa. Stoga su marginalni vektori jedinstveno određeni brojem fiksnih točaka i pravaca. U idućem odjeljku bavimo se fiksnim strukturama automorfizma prostog reda.