Mario Bukal: Ocjena greške za metodu konačnih volumnih elemenata, travanj 2008. (pdf)
FreeFem++ can also handle other numerical techniques for partial differential equations but it requires programming.
Here we present the finite volume element method for the following elliptic boundary value problem:
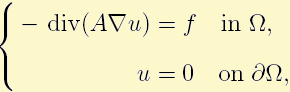
where 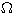 is a bounded convex polygonal domain, A is a symmetric and uniformly positive definite matrix in
is a bounded convex polygonal domain, A is a symmetric and uniformly positive definite matrix in 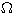 , and function f has enough regularity so that this boundary value problem has a unique
solution in a certain Sobolev space.
, and function f has enough regularity so that this boundary value problem has a unique
solution in a certain Sobolev space.
Let 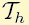 be regular triangulation on
be regular triangulation on  consisting of triangles. Dual mesh
consisting of triangles. Dual mesh 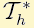 , based on
, based on 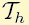 , is then introduced as Donald diagram.
, is then introduced as Donald diagram.
We seek approximate solution 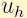 in space of functions that are linear on every
in space of functions that are linear on every  , vanish on the boundary and are globaly continuous. Integrating upper equation over an arbitrary
, vanish on the boundary and are globaly continuous. Integrating upper equation over an arbitrary 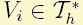 and using Gauss's divergence theorem we have
and using Gauss's divergence theorem we have
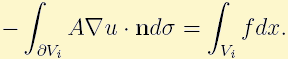
Discretization of left hand side in last equation leads to a linear equation. Repeating the above procedure for every control volume, we obtain a system of linear equations with values of 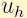 in vertices of
in vertices of 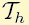 as unknowns.
as unknowns.
We have to program an external C++ functions for FreeFem++. This is done as explained in manual for FreeFem++ (Appendix A). Stiffnes matrix in FVEM is assebled by an external C++ function MatrixFVEM() and right hand side vector is computed by an external C++ function RHS(). MatrixFVEM() is programmed as follows:
This code is inserted into a larger .cpp file mat_fvm.cpp which is the load module linked to FreeFem++.
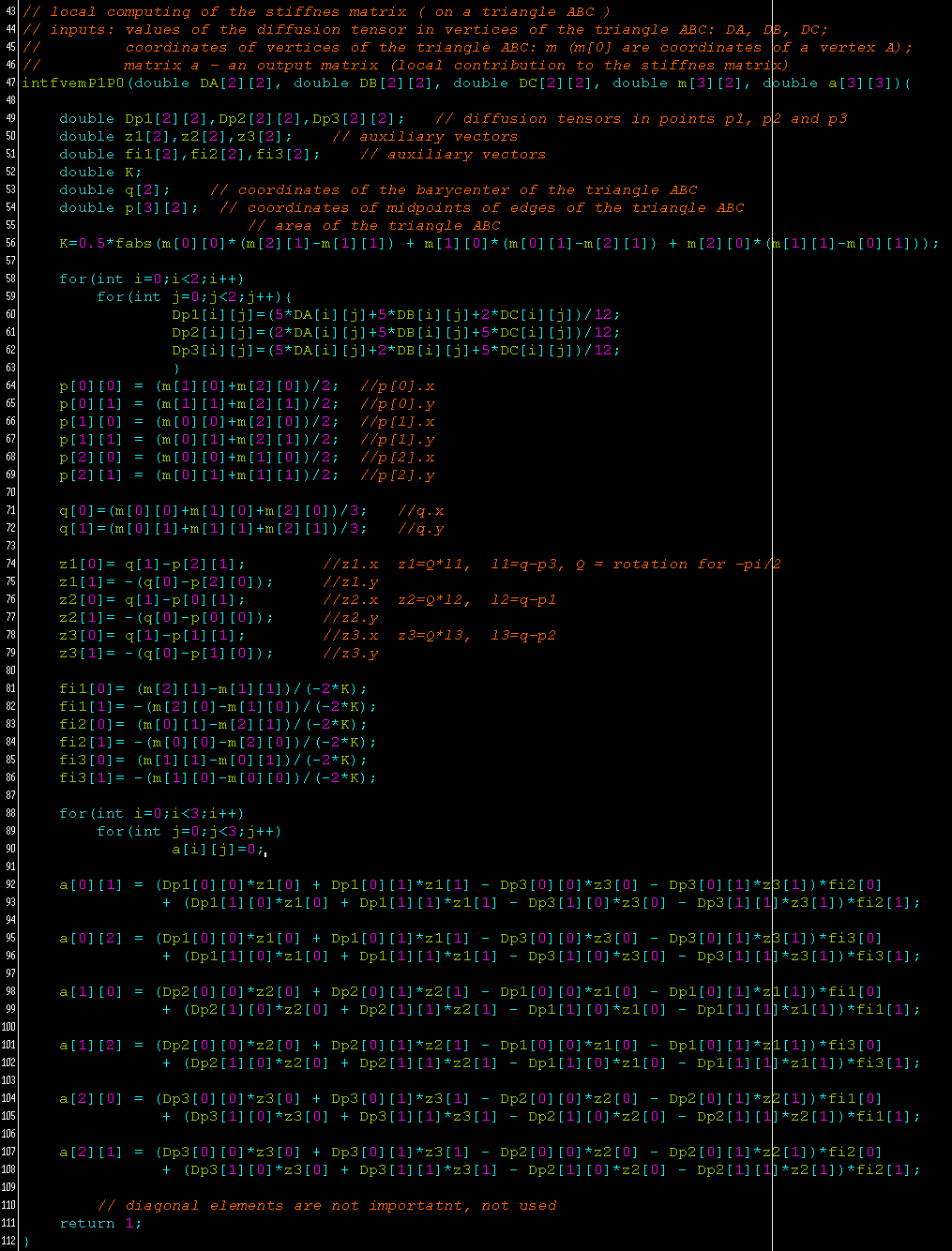
Next, function RHS() is programmed as:
In a similar way, this code is inserted into .cpp file mat_source.cpp which is also the load module linked to FreeFem++.
./load.link mat_fvm.cpp ./load.link mat_source.cpp
load "mat_fvm"; load "mat_source";
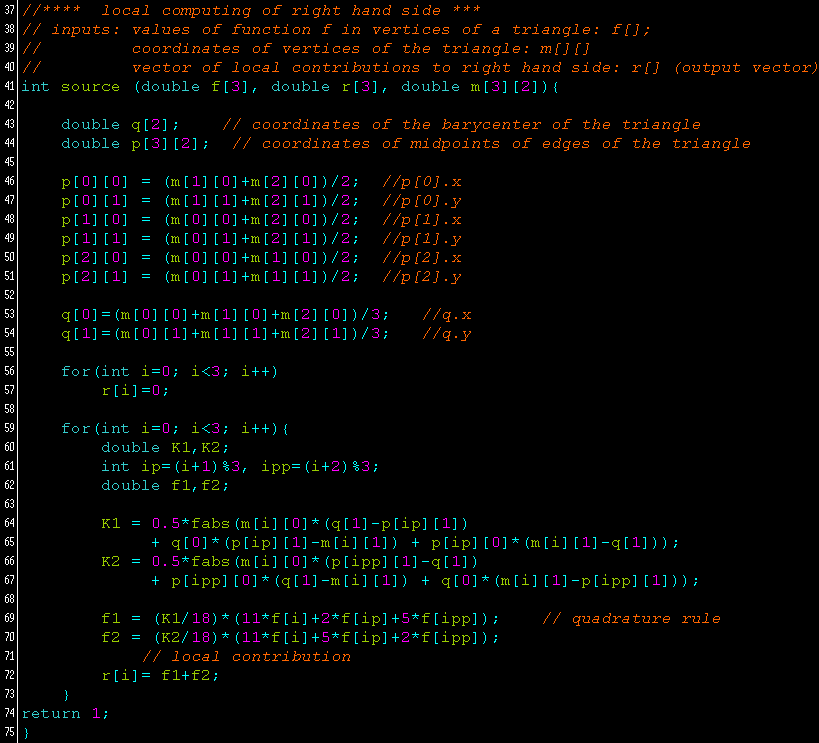
Let  be the unit square. Solve the following Dirichlet problem:
be the unit square. Solve the following Dirichlet problem:
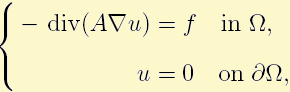
where matrix 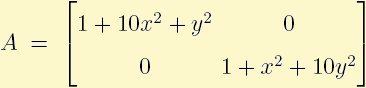 and function f
is computed bay taking the exact solution
and function f
is computed bay taking the exact solution 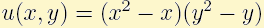 .
.

Complete .edp file of the example can be downloaded from here.