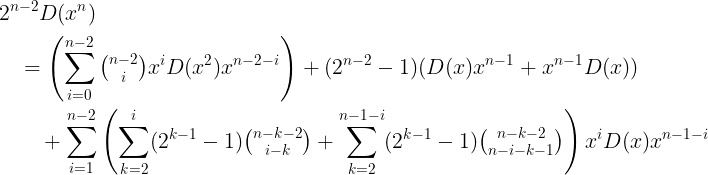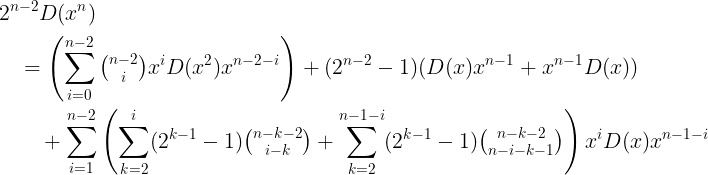Glasnik Matematicki, Vol. 56, No. 1 (2021), 95-106.

A RESULT RELATED TO DERIVATIONS ON UNITAL SEMIPRIME RINGS

Irena Kosi-Ulbl, Nejc Širovnik and Joso Vukman

Faculty of Mechanical Engineering, University of Maribor, Smetanova 17, 2000 Maribor, Slovenia
e-mail: irena.kosi@um.si

WinSystems, Global Gaming Solutions Partner
e-mail: nejc.sirovnik@gmail.com

Faculty of Natural Sciences and Mathematics, Department of Mathematics and Computer Science, University of Maribor, Koroška 160, 2000 Maribor, Slovenia
e-mail: joso.vukman@guest.um.si

Abstract.   The purpose of this paper is to prove the following result. Let n≥3 be some fixed integer and let R be a (n+1)!2n-2-torsion free semiprime unital ring. Suppose there exists an additive mapping D: R→ R satisfying the relation


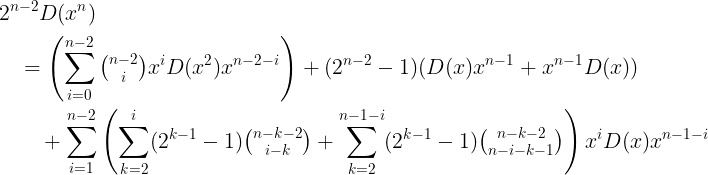
for all x ∈ R. In this case D is a derivation. The history of this result goes back to a classical result of Herstein, which states that any Jordan derivation on a 2-torsion free prime ring is a derivation.

2010 Mathematics Subject Classification.   16N60, 39B52

Key words and phrases.   Prime ring, semiprime ring, derivation, Jordan derivation

Full text (PDF) (access from subscribing institutions only)

https://doi.org/10.3336/gm.56.1.07

References:

  1. D. Alvo and R. Pellicer, Modified Pascal triangle and Pascal surfaces, http://www.academia.edu/956605.

  2. K. I. Beidar, M. Brešar, M. A. Chebotar and W. S. Martindale 3rd, On Herstein's Lie map conjectures II, J. Algebra 238 (2001), 239-264.
    MathSciNet     CrossRef

  3. M. Brešar and J. Vukman, Jordan derivations on prime rings, Bull. Austral. Math. Soc. 37 (1988), 321-322.
    MathSciNet     CrossRef

  4. M. Brešar, Jordan derivations on semiprime rings, Proc. Amer. Math. Soc. 104 (1988), 1003-1006.
    MathSciNet     CrossRef

  5. M. Brešar, Jordan mappings of semiprime rings, J. Algebra 127 (1989), 218-228.
    MathSciNet     CrossRef

  6. J. Cusack, Jordan derivations on rings, Proc. Amer. Math. Soc. 53 (1975), 321-324.
    MathSciNet     CrossRef

  7. B. Ebanks, Characterizing ring derivations of all orders via functional equations: results and open problems, Aequationes Math. 89 (2015), 685-718.
    MathSciNet     CrossRef

  8. B. Ebanks, T. Riedel and P. K. Sahoo, On the order of a derivation, Aequationes Math. 90 (2016), 335-340.
    MathSciNet     CrossRef

  9. B. Ebanks, Functional equations characterizing derivations: a synthesis, Results Math. 73 (2018), No. 120, 13 pp.
    MathSciNet     CrossRef

  10. D. Eremita, I. Kosi-Ulbl and J. Vukman, On certain equations in rings, Bull. Austral. Math. Soc. 71 (2005), 53-60.
    MathSciNet     CrossRef

  11. M. Fošner, N. Širovnik and J.Vukman, A result related to Herstein theorem, Bull. Malays. Math. Sci. Soc. 39 (2016), 885-899.
    MathSciNet     CrossRef

  12. E. Gselmann, G. Kiss and Cs. Vincze, On functional equations characterizing derivations: methods and examples, Results Math. 73 (2018), No. 74, 27 pp.
    MathSciNet     CrossRef

  13. I. N. Herstein, Jordan derivations of prime rings, Proc. Amer. Math. Soc. 8 (1957), 1104-1120.
    MathSciNet     CrossRef

  14. I. Kosi-Ulbl and J. Vukman, An equation related to centralizers in semiprime rings, Glas. Mat. Ser. III 38(58) (2003), 253-261.
    MathSciNet     CrossRef

  15. I. Kosi-Ulbl and J. Vukman, A note on derivations in semiprime rings, Int. J. Math. Math. Sci. 20 (2005), 3347-3350.
    MathSciNet     CrossRef

  16. C.-K. Liu and W.-K. Shiue, Generalized Jordan triple (θ,φ)-derivations on semiprime rings, Taiwanese J. Math. 11 (2007), 1397-1406.
    MathSciNet     CrossRef

  17. J. Vukman, Centralizers on semiprime rings, Comment. Math. Univ. Carolin. 42 (2001), 237-245.
    MathSciNet    

  18. J. Vukman, Some remarks on derivations in semiprime rings and standard operator algebras, Glas. Mat. Ser. III 46(66) (2011), 43-48.
    MathSciNet     CrossRef
Glasnik Matematicki Home Page