Glasnik Matematicki, Vol. 54, No. 2 (2019), 369-407.
TWISTED HEISENBERG-VIRASORO VERTEX OPERATOR ALGEBRA
Hongyan Guo and Qing Wang
School of Mathematics and Statistics,
Central China Normal University,
Wuhan 430079,
China
School of Mathematical Sciences,
Xiamen University,
Xiamen 361005,
China
Abstract.
In this paper, we study a new kind of vertex operator algebras related to twisted Heisenberg-Virasoro algebra.
We showed that there exist one-to-one correspondences between the restricted module categories of twisted Heisenberg-Virasoro algebras of rank one and rank two
and several different kinds of module categories of their corresponding vertex algebras. We also study in detail the structures of the twisted Heisenberg-Virasoro vertex operator algebra and
give a characterization
of it as a tensor product of two well-known vertex operator algebras.
2010 Mathematics Subject Classification. 17B69
Key words and phrases. Twisted Heisenberg-Virasoro algebra, vertex operator algebra, modules
Full text (PDF) (free access)
https://doi.org/10.3336/gm.54.2.06
References:
- T. Abe, G. Buhl and C. Dong, Rationality, regularity, and C2-cofiniteness,
Trans. Amer. Math. Soc. 356 (2004), 3391-3402.
MathSciNet
CrossRef
- E. Arbarello, C. De Concini, V. Kac and C. Procesi, Moduli spaces of curves and representation theory,
Comm. Math. Phys. 117 (1988), 1-36.
MathSciNet
CrossRef
-
D. Adamović and G. Radobolja, Free field realization of the twisted Heisenberg-Virasoro algebra at level zero and its applications,
J. Pure and Appl. Algebra 219 (2015), 4322-4342.
MathSciNet
CrossRef
-
D. Adamović and G. Radobolja, Self-dual and logarithmic representations of the twisted Heisenberg-Virasoro algebra at level zero,
Commun. Contemp. Math. 21 (2019), 1850008, 26pp.
MathSciNet
CrossRef
- Y. Billig, Representations of the twisted Heisenberg-Virasoro algebra at level zero,
Canad. Math. Bull. 46 (2003), 529-537.
MathSciNet
CrossRef
- Y. Billig, A category of modules for the full toroidal Lie algebra,
Int. Math. Res. Not. 2006, Art. ID. 68395, 46pp.
MathSciNet
CrossRef
-
S. Berman, Y. Billig and J. Szmigielski, Vertex operator algebras and the representation theory of toroidal algebras,
Contemporary Math. 297, Amer. Math. Soc., Providence, 2002, 1-26.
MathSciNet
CrossRef
-
C. Dong and J. Lepowsky, Generalized vertex algebras and relative vertex operators,
Birkhauser Boston, Inc., Boston, 1993.
MathSciNet
CrossRef
- C. Dong and X.Lin, Unitary vertex operator algebras,
J. Algebra 397 (2014), 252-277.
MathSciNet
CrossRef
-
C. Dong and Q. Wang, The structure of parafermion vertex operator algebras,
Commun. Math. Phys. 299 (2010), 783-792.
MathSciNet
CrossRef
-
C. Dong, H. Li and G. Mason, Regularity of rational vertex operator algebra,
Adv. Math. 312 (1997), 148-166.
MathSciNet
CrossRef
-
C. Dong, H. Li and G. Mason, Twisted representations of vertex operator algebras,
Math. Ann. 310 (1998), 571-600.
MathSciNet
CrossRef
-
I. Frenkel, Y. Huang and J. Lepowsky, On axiomatic approaches to vertex operator algebras and modules,
Mem. Amer. Math. Soc. 104 (1993), no. 494, Viii+64 pp.
MathSciNet
CrossRef
- I. Frenkel, J. Lepowsky and A. Meurman, Vertex operator algebras and the Monster,
Academic Press, Inc., Boston, 1988.
MathSciNet
-
I. B. Frenkel and Y. Zhu, Vertex operator algebras associated to representations
of affine and Virasoro algebras, Duke Math. J. 66 (1992), 123-168.
MathSciNet
CrossRef
- M. Golenishcheva-Kutuzova and V. Kac, γ-conformal algebras,
J. Math. Phys. 39 (1998), 2290-2305.
MathSciNet
CrossRef
- P. Goddard, A. Kent and D. Olive, Virasoro algebras and coset space models,
Phys. Lett. B 152 (1985), 88-92.
MathSciNet
CrossRef
-
H. Guo, H. Li, S. Tan and Q. Wang, q-Virasoro algebra and vertex algebras, J. Pure Appl. Algebra 219 (2015), 1258-1277.
MathSciNet
CrossRef
-
H. Guo and Q. Wang, Associating vertex algebras to the unitary Lie algebra, J. Algebra 424 (2015), 126-146.
MathSciNet
CrossRef
-
C. Jiang and H. Li, Associating quantum vertex algebras to Lie algebra 𝔤𝔩∞,
J. Algebra 399 (2014), 1086-1106.
MathSciNet
CrossRef
-
C. Jiang and Z. Lin, The commutant of L
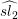 (n,0) in the vertex operator algebra L
(n,0) in the vertex operator algebra L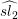 (1,0)⊗ n,
Adv. Math. 301 (2016), 227-257.
(1,0)⊗ n,
Adv. Math. 301 (2016), 227-257.
MathSciNet
CrossRef
-
V. Kac and D. Peterson, Infinite-dimensional Lie algebra, theta functions and modular forms,
Adv. Math. 53 (1984), 125-264.
MathSciNet
CrossRef
-
B. Lian and A. Linshaw, Howe pairs in the theory of vertex algebras,
J. Algebra 317 (2007), 111-152.
MathSciNet
CrossRef
- J. Lepowsky and H. Li, Introduction to vertex operator algebras
and their representations, Birkhäuser, Inc., Boston, 2004.
MathSciNet
CrossRef
- H. Li, A new construction of vertex algebras and quasi modules
for vertex algebras, Adv. Math. 202 (2006), 232-286.
MathSciNet
CrossRef
- H. Li, On certain generalizations of twisted affine Lie algebras and quasimodules for γ-vertex algebras, J. Pure Appl. Algebra 209 (2007), 853-871.
MathSciNet
CrossRef
- H. Li, Local systems of vertex operators, vertex superalgebras and modules,
J. Pure Appl. Algebra 109 (1996), 143-195.
MathSciNet
CrossRef
- H. Li, φ-coordinated quasi-modules for quantum vertex algebras,
Comm. Math. Phys. 308 (2011), 703-741.
MathSciNet
CrossRef
- H. Li, G-equivariant φ-coordinated quasi-modules for quantum vertex algebras,
J. Math. Phys. 54 (2013), 051704, 26 pp.
MathSciNet
CrossRef
- H. Li, Nonlocal vertex algebras generated by formal vertex operators,
Selecta Math. (N.S.) 11 (2005), 349-397.
MathSciNet
CrossRef
- H. Li, Some finiteness properties of regular vertex operator algebras,
J. Algebra 212 (1999), 495-514.
MathSciNet
CrossRef
- H. Li, S. Tan and Q. Wang, Toroidal vertex algebras and their modules,
J. Algebra 365 (2012) 50-82.
MathSciNet
CrossRef
- M. Xue, W. Lin and S. Tan, Central extension, derivations and automorphism group for
Lie algebras arising from 2-dimensional torus, J. Lie Theory 16 (2006), 139-153.
MathSciNet
- V. Kac and Rehana, Bombay lectures on highest weight representation of infinite dimensional Lie algebras, World Scientific Publishing Co., Inc., Teaneck, 1987.
MathSciNet
- W. Wang, Rationality of Virasoro vertex operator algebras,
Internat. Math. Res. Notices 1993, 197-211.
MathSciNet
CrossRef
- Y. Zhu, Modular invariance of characters of vertex operator algebras,
J. Amer. Math. Soc 9 (1996), 237-302.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
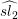 (n,0) in the vertex operator algebra L
(n,0) in the vertex operator algebra L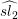 (1,0)⊗ n,
Adv. Math. 301 (2016), 227-257.
(1,0)⊗ n,
Adv. Math. 301 (2016), 227-257.