Glasnik Matematicki, Vol. 54, No. 1 (2019), 133-178.
AUBERT DUALS OF DISCRETE SERIES: THE FIRST INDUCTIVE STEP
Ivan Matić
Department of Mathematics, University of Osijek, Trg Ljudevita Gaja 6, 31 000 Osijek, Croatia
e-mail: imatic@mathos.hr
Abstract.
Let Gn denote either symplectic or odd special orthogonal group of rank n over a non-archimedean local field F. We provide an explicit description of the Aubert duals of irreducible representations of Gn which occur in the first inductive step in the realization of discrete series representations starting from the strongly positive ones. Our results might serve as a pattern for determination of Aubert duals of general discrete series of Gn and should produce an interesting part of the unitary dual of this group. Furthermore, we obtain an explicit form of some representations which are known to be unitarizable.
2010 Mathematics Subject Classification. 22E35, 22E50, 11F70
Key words and phrases. Aubert dual, discrete series, classical p-adic groups
Full text (PDF) (free access)
https://doi.org/10.3336/gm.54.1.07
References:
-
J. Arthur, The endoscopic classification of representations. Orthogonal and
symplectic groups, American Mathematical Society, Providence, 2013.
MathSciNet
CrossRef
-
A.-M. Aubert, Dualité dans le groupe de Grothendieck de la catégorie
des représentations lisses de longueur finie d'un groupe réductif
p-adique, Trans. Amer. Math. Soc. 347 (1995), 2179-2189.
MathSciNet
CrossRef
-
A.-M. Aubert, Erratum: ``Duality in the Grothendieck group of the
category of finite-length smooth representations of a p-adic reductive
group'' [Trans. Amer. Math. Soc. 347 (1995), no. 6,
2179-2189; MR1285969 (95i:22025)], Trans. Amer. Math. Soc. 348 (1996), 4687-4690.
MathSciNet
CrossRef
-
W. T. Gan and L. Lomelí, Globalization of supercuspidal
representations over function fields and applications, J. Eur. Math. Soc.
(JEMS) 20 (2018), 2813-2858.
MathSciNet
CrossRef
-
M. Hanzer, Unitarizability of a certain class of irreducible
representations of classical groups, Manuscripta Math. 127
(2008), 275-307.
MathSciNet
CrossRef
-
M. Hanzer, The unitarizability of the Aubert dual of strongly positive
square integrable representations, Israel J. Math. 169 (2009),
251-294.
MathSciNet
CrossRef
-
C. Jantzen, Reducibility of certain representations for symplectic and
odd-orthogonal groups, Compositio Math. 104 (1996), 55-63.
MathSciNet
CrossRef
-
C. Jantzen, Duality for classical p-adic groups: the half-integral
case, Represent. Theory 22 (2018), 160-201.
MathSciNet
CrossRef
-
Y. Kim and I. Matić, Discrete series of odd general spin groups,
preprint, 2018.
-
H. Knight and A. Zelevinsky, Representations of quivers of type A and
the multisegment duality, Adv. Math. 117 (1996), 273-293.
MathSciNet
CrossRef
-
A. Kret and E. Lapid, Jacquet modules of ladder representations, C. R.
Math. Acad. Sci. Paris 350 (2012), 937-940.
MathSciNet
CrossRef
-
I. Matić, Strongly positive representations of metaplectic groups, J.
Algebra 334 (2011), 255-274.
MathSciNet
CrossRef
-
I. Matić, The conservation relation for discrete series
representations of metaplectic groups, Int. Math. Res. Not. IMRN 2013,
5227-5269.
MathSciNet
CrossRef
-
I. Matić, Jacquet modules of strongly positive representations of the
metaplectic group
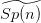 , Trans. Amer. Math. Soc. 365 (2013), 2755-2778.
, Trans. Amer. Math. Soc. 365 (2013), 2755-2778.
MathSciNet
CrossRef
-
I. Matić, On discrete series subrepresentations of the generalized
principal series, Glas. Mat. Ser. III 51(71) (2016), 125-152.
MathSciNet
CrossRef
-
I. Matić, On Jacquet modules of discrete series: the first inductive
step, J. Lie Theory 26 (2016), 135-168.
MathSciNet
-
I. Matić, Aubert duals of strongly positive discrete series and a
class of unitarizable representations, Proc. Amer. Math. Soc. 145 (2017), 3561-3570.
MathSciNet
CrossRef
-
I. Matić, On Langlands quotients of the generalized principal series
isomorphic to their Aubert duals, Pacific J. Math. 289 (2017),
395-415.
MathSciNet
CrossRef
-
I. Matić and M. Tadić, On Jacquet modules of representations of
segment type, Manuscripta Math. 147 (2015), 437-476.
MathSciNet
CrossRef
-
C. Mœglin, Sur la classification des séries discrètes des groupes
classiques p-adiques: paramètres de Langlands et exhaustivité, J.
Eur. Math. Soc. (JEMS) 4 (2002), 143-200.
MathSciNet
CrossRef
-
C. Mœglin, Paquets stables des séries discrètes accessibles par
endoscopie tordue; leur paramètre de Langlands, in: Automorphic forms and
related geometry: assessing the legacy of I. I. Piatetski-Shapiro,
Amer. Math. Soc., Providence, 2014,
295-336.
MathSciNet
CrossRef
-
C. Mœglin and M. Tadić, Construction of discrete series for
classical p-adic groups, J. Amer. Math. Soc. 15 (2002), 715-786.
MathSciNet
CrossRef
-
C. Mœglin and J.-L. Waldspurger, Sur l'involution de Zelevinski, J.
Reine Angew. Math. 372 (1986), 136-177.
MathSciNet
CrossRef
-
G. Muić, Composition series of generalized principal series; the case
of strongly positive discrete series, Israel J. Math. 140
(2004), 157-202.
MathSciNet
CrossRef
-
G. Muić, On certain classes of unitary representations for split
classical groups, Canad. J. Math. 59 (2007), 148-185.
MathSciNet
CrossRef
-
M. Tadić, Structure arising from induction and Jacquet modules of
representations of classical p-adic groups, J. Algebra 177
(1995), 1-33.
MathSciNet
CrossRef
-
M. Tadić, On reducibility of parabolic induction, Israel J. Math.
107 (1998), 29-91.
-
M. Tadić, On tempered and square integrable representations of
classical p-adic groups, Sci. China Math. 56 (2013), 2273-2313.
MathSciNet
CrossRef
-
A. V. Zelevinsky, Induced representations of reductive p-adic groups.
II. On irreducible representations of GL(n), Ann. Sci. École
Norm. Sup. (4) 13 (1980), 165-210.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
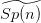 , Trans. Amer. Math. Soc. 365 (2013), 2755-2778.
, Trans. Amer. Math. Soc. 365 (2013), 2755-2778.