Glasnik Matematicki, Vol. 54, No. 1 (2019), 11-20.
EXPLICIT BOUNDS FOR COMPOSITE LACUNARY POLYNOMIALS
Christina Karolus
Department of Mathematics, University of Salzburg, 5020 Salzburg, Austria
e-mail: christina.karolus@sbg.ac.at
Abstract.
Let f, g, h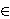 ℂ [x] be non-constant complex polynomials satisfying f(x)=g(h(x)) and let f be lacunary in the sense that it has at most l non-constant terms. Zannier proved in [9] that there exists a function B1(l) on ℕ, depending only on l and with the property that h(x) can be written as the ratio of two polynomials having each at most B1(l) terms. Here, we give explicit estimates for this function or, more precisely, we prove that one may take for instance
ℂ [x] be non-constant complex polynomials satisfying f(x)=g(h(x)) and let f be lacunary in the sense that it has at most l non-constant terms. Zannier proved in [9] that there exists a function B1(l) on ℕ, depending only on l and with the property that h(x) can be written as the ratio of two polynomials having each at most B1(l) terms. Here, we give explicit estimates for this function or, more precisely, we prove that one may take for instance
B1(l)=(4l)(2l)(3l)l+1.
Moreover, in the case l=2, a better bound is obtained using the same strategy.
2010 Mathematics Subject Classification. 11C08, 11R09
Key words and phrases. Decomposable polynomials, lacunary polynomials
Full text (PDF) (free access)
https://doi.org/10.3336/gm.54.1.02
References:
- D. Dona, On lacunary polynomials and a generalization of Schinzel's conjecture, Master thesis, Concordia University/Université de Bordeaux, 2015.
- C. Fuchs and L. Hajdu, 30 years of collaboration, Period. Math. Hung. 74 (2017), 255-274.
MathSciNet
CrossRef
- C. Fuchs, V. Mantova and U. Zannier, On fewnomials, integral points and a toric version of Bertini's theorem J. Amer. Math. Soc. 31 (2018), 107-134.
MathSciNet
CrossRef
- C. Fuchs and A. Pethö , Composite rational functions having a bounded number of zeros and poles, Proc. Amer. Math. Soc. 139 (2011), 31-38.
MathSciNet
CrossRef
- C. Fuchs and U. Zannier, Composite rational functions expressible with few terms, J. Eur. Math. Soc. 14 (2012), 175-208.
MathSciNet
CrossRef
- A. Pethö and S. Tengely, On composite rational functions, in: Number theory, analysis, and combinatorics, De Gruyter Proc. Math., De Gruyter, Berlin, 2014, 241-259.
MathSciNet
- A. Schinzel, On the number of terms of a power of a polynomial, Acta Arith. 49 (1987), 55-70.
MathSciNet
CrossRef
- U. Zannier, On the number of terms of a composite polynomial, Acta Arith. 127 (2007), 157-167.
MathSciNet
CrossRef
- U. Zannier, On composite lacunary polynomials and the proof of a conjecture of Schinzel, Invent. Math. 174 (2008), 127-138.
MathSciNet
CrossRef
- U. Zannier, Addendum to the paper: On the number of terms of a composite polynomial, Acta Arith. 140 (2009), 93-99.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
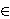 ℂ [x] be non-constant complex polynomials satisfying f(x)=g(h(x)) and let f be lacunary in the sense that it has at most l non-constant terms. Zannier proved in [9] that there exists a function B1(l) on ℕ, depending only on l and with the property that h(x) can be written as the ratio of two polynomials having each at most B1(l) terms. Here, we give explicit estimates for this function or, more precisely, we prove that one may take for instance
ℂ [x] be non-constant complex polynomials satisfying f(x)=g(h(x)) and let f be lacunary in the sense that it has at most l non-constant terms. Zannier proved in [9] that there exists a function B1(l) on ℕ, depending only on l and with the property that h(x) can be written as the ratio of two polynomials having each at most B1(l) terms. Here, we give explicit estimates for this function or, more precisely, we prove that one may take for instance