Glasnik Matematicki, Vol. 53, No. 1 (2018), 143-151.
PROPER INCLUSIONS OF MORREY SPACES
Hendra Gunawan, Denny Ivanal Hakim
and Mochammad Idris
Department of Mathematics, Bandung Institute of Technology,
Bandung 40132, Indonesia
e-mail: hgunawan@math.itb.ac.id
e-mail: dennyivanalhakim@gmail.com
e-mail: idemath@gmail.com
Abstract.
In this paper, we prove that the inclusions between Morrey spaces, between
weak Morrey spaces, and between a Morrey space and a weak Morrey space are all proper.
The proper inclusion between a Morrey space and a weak Morrey space is established
via the unboundedness of the Hardy-Littlewood maximal operator on Morrey spaces
of exponent 1. In addition, we also give a necessary condition for each inclusion.
Our results refine previous inclusion properties studied in [4].
2010 Mathematics Subject Classification.
42B35, 46E30.
Key words and phrases. Morrey spaces, weak Morrey spaces, inclusion properties.
Full text (PDF) (free access)
DOI: 10.3336/gm.53.1.10
References:
-
F. Chiarenza and M. Frasca, Morrey spaces and Hardy-Littlewood
maximal function, Rend. Mat. Appl. (7) 7 (1987), 273-279.
MathSciNet
-
H. Gunawan, A note on the generalized fractional integral
operators, J. Indones. Math. Soc. 9 (2003), 39-43.
MathSciNet
-
H. Gunawan, D. I. Hakim, Y. Sawano and I. Sihwaningrum, Weak type inequalities for some integral operators on generalized nonhomogeneous Morrey spaces, J. Funct. Spaces Appl. 2013, Art. ID 809704, 12 pp.
MathSciNet
-
H. Gunawan, D. I. Hakim, K. M. Limanta and A. A. Masta, Inclusion
properties of generalized Morrey spaces, Math. Nachr. 290
(2017), 332-340.
MathSciNet
CrossRef
-
D. I. Hakim and H. Gunawan, Weak (p,q) inequalities for fractional integral operators on generalized Morrey spaces of non-homogeneous type, Math. Aeterna 3 (2013), 161-168.
MathSciNet
-
D. D. Haroske and L. Skrzypczak, Embeddings of weighted Morrey
spaces, Math. Nachr. 290 (2017), 1066-1086.
MathSciNet
CrossRef
-
C. B. Morrey, Jr., On the solutions of quasi-linear
elliptic partial differential equations, Trans. Amer. Math. Soc.
43 (1938), 126-166.
MathSciNet
CrossRef
-
E. Nakai, Orlicz-Morrey spaces and the Hardy-Littlewood maximal
function, Studia Math. 188 (2008), 193-221.
MathSciNet
CrossRef
-
J. Peetre, On the theory of
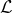 p,Λ spaces,
J. Functional Analysis 4 (1969), 71-87.
p,Λ spaces,
J. Functional Analysis 4 (1969), 71-87.
MathSciNet
-
L. C. Piccinini, Proprietä di Inclusione e Interpolazione tra
Spazi di Morrey e loro Generalizzazioni,
Tesi di perfezionamento, Scuola Normale Superior Pisa, 1969.
-
L. C. Piccinini, Inclusioni tra spazi di Morrey, Boll. Un.
Mat. Ital. (4) 2 (1969), 95-99.
MathSciNet
-
M. Rosenthal, Morrey-Räume aus der Sicht der Harmonischen Analysis,
Master thesis, Friedrich-Schiller-Universität Jena, 2009.
Glasnik Matematicki Home Page
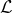 p,Λ spaces,
J. Functional Analysis 4 (1969), 71-87.
p,Λ spaces,
J. Functional Analysis 4 (1969), 71-87.