Glasnik Matematicki, Vol. 53, No. 1 (2018), 115-121.
PRESENTATIONS OF FEIGIN-STOYANOVSKY'S TYPE SUBSPACES OF STANDARD MODULES FOR AFFINE LIE ALGEBRAS OF TYPE Cl(1)
Goran Trupčević
Faculty of Teacher Education, University of Zagreb, 10000 Zagreb, Croatia
e-mail: goran.trupcevic@ufzg.hr
Abstract.
Feigin-Stoyanovsky's type subspace W(Λ) of a standard  -module L(Λ) is a
-module L(Λ) is a  1-submodule of L(Λ) generated by
the highest-weight vector vΛ, where
1-submodule of L(Λ) generated by
the highest-weight vector vΛ, where  1 is a certain commutative subalgebra of
1 is a certain commutative subalgebra of  . Based on the description of basis of
W(Λ) for
. Based on the description of basis of
W(Λ) for  of type Cl(1), we give a presentation of this subspace in terms of generators and relations
W(Λ)≃ U(
of type Cl(1), we give a presentation of this subspace in terms of generators and relations
W(Λ)≃ U( 1-)/J.
1-)/J.
2010 Mathematics Subject Classification.
17B67, 17B69, 05A19.
Key words and phrases. Affine Lie algebras, principal subspaces, generators and relations.
Full text (PDF) (free access)
DOI: 10.3336/gm.53.1.08
References:
- E. Ardonne, R. Kedem and M. Stone, Fermionic characters and arbitrary highest-weight integrable
 r+1-modules,
Comm. Math. Phys. 264 (2006), 427-464.
r+1-modules,
Comm. Math. Phys. 264 (2006), 427-464.
MathSciNet
CrossRef
- I. Baranović, Combinatorial bases of Feigin-Stoyanovsky's type subspaces of level 2 standard modules for D4(1),
Comm. Algebra 39 (2011), 1007-1051.
MathSciNet
CrossRef
- I. Baranović, M. Primc and G. Trupčević, Bases of Feigin-Stoyanovsky's type subspaces for Cl(1), Ramanujan J (2016). doi:10.1007/s11139-016-9840-y 1007-1051.
- M. Butorac, Combinatorial bases of principal subspaces for the affine Lie algebra of type B2(1), J. Pure Appl. Algebra 218 (2014), 424-447.
MathSciNet
CrossRef
- M. Butorac, Quasi particle bases of principal subspaces of the affine Lie algebra of type G2(1),
Glas. Mat. Ser. III 52(72) (2017), 79-98.
MathSciNet
CrossRef
- C. Calinescu, Intertwining vertex operators and certain representations of
 , Commun. Contemp. Math. 10 (2008), 47-79.
, Commun. Contemp. Math. 10 (2008), 47-79.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of the principal subspaces of certain A1(1)-modules, I. Level one case, Internat. J. Math. 19 (2008), 71-92.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of the principal subspaces of certain A1(1)-modules, II. Higher-level case, J. Pure Appl. Algebra 212 (2008), 1928-1950.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of the principal subspaces of level one modules for the untwisted affine Lie algebras of types A, D, E, J. Algebra 323 (2010), 167-192.
MathSciNet
CrossRef
- S. Capparelli, J. Lepowsky and A. Milas,
The Rogers-Ramanujan recursion and intertwining operators,
Commun. Contemp. Math. 5 (2003), 947-966.
MathSciNet
CrossRef
- S. Capparelli, J. Lepowsky and A. Milas,
The Rogers-Selberg recursions, the Gordon-Andrews identities and intertwining operators, Ramanujan J. 12 (2006), 379-397.
MathSciNet
CrossRef
- A. V. Stoyanovsky and B. L. Feigin, Functional models of the representations of current algebras, and semi-infinite Schubert cells, (Russian) Funktsional. Anal. i Prilozhen. 28 (1994), 68-90; translation in Funct. Anal. Appl. 28 (1994), 55-72.
MathSciNet
CrossRef
- B. Feigin, M. Jimbo, S. Loktev, T. Miwa and E. Mukhin, Bosonic formulas for (k,l)-admissible partitions, Ramanujan J. 7 (2003), 485-517.; Addendum to `Bosonic formulas for (k,l)-admissible partitions', Ramanujan J. 7 (2003), 519-530.
MathSciNet
CrossRef
- B. Feigin, M. Jimbo, T. Miwa, E. Mukhin and Y. Takeyama, Fermionic formulas for (k,3)-admissible configurations, Publ. Res. Inst. Math. Sci. 40 (2004), 163-220.
MathSciNet
CrossRef
- G. Georgiev,
Combinatorial constructions of modules for
infinite-dimensional Lie algebras. I. Principal subspace, J. Pure
Appl. Algebra 112 (1996), 247-286.
MathSciNet
CrossRef
- J. Humphreys
Introduction to Lie algebras and representation theory, Springer, New-York, 1978.
MathSciNet
- M. Jerković,
Recurrence relations for characters of affine
Lie algebra Al(1), J. Pure Appl. Algebra 213,
913-926.
MathSciNet
CrossRef
- M. Jerković and M. Primc, Quasi-particle fermionic formulas for (k, 3)-admissible configurations,
Cent. Eur. J. Math. 10 (2012), 703-721.
MathSciNet
CrossRef
- V. G. Kac,
Infinite-dimensional Lie algebras, Cambridge
University Press, Cambridge, 1990.
MathSciNet
CrossRef
- J. Lepowsky and H.-S. Li,
Introduction to vertex operator algebras
and their representations, Birkhäuser, Boston, 2004.
MathSciNet
CrossRef
-
J. Lepowsky and M. Primc,
Structure of the standard modules for
the affine Lie algebra A1(1), Contemporary Mathematics
46, American Mathematical Society, 1985.
MathSciNet
CrossRef
- A. Meurman and M. Primc, Annihilating fields of standard modules of
 (2,ℂ)˜ and combinatorial identities, Mem. Amer. Math. Soc. 652, 1999.
(2,ℂ)˜ and combinatorial identities, Mem. Amer. Math. Soc. 652, 1999.
MathSciNet
CrossRef
- M. Penn, Lattice vertex superalgebras, I: Presentation of the principal subalgebra,
Comm. Algebra 42 (2014), 933-961.
MathSciNet
CrossRef
- M. Primc, Vertex operator construction of standard modules
for An(1), Pacific J. Math. 162 (1994), 143-187.
MathSciNet
CrossRef
- M. Primc, Basic representations for classical
affine Lie algebras, J. Algebra 228 (2000), 1-50.
MathSciNet
CrossRef
- M. Primc, Combinatorial bases of modules
for affine Lie algebra B2(1), Cent. Eur. J. Math. 11 (2013), 197-225.
MathSciNet
CrossRef
- C. Sadowski, Presentations of the principal subspaces of the higher level standard
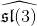 -modules, J. Pure
Appl. Algebra 219 (2015), 2300-2345.
-modules, J. Pure
Appl. Algebra 219 (2015), 2300-2345.
MathSciNet
CrossRef
- A. V. Stoyanovsky, Lie algebra deformations and character formulas
(Russian) Funktsional. Anal. i Prilozhen. 32 (1998), 84-86; translation in Funct. Anal. Appl. 32 (1998), 66-68.
MathSciNet
CrossRef
- G. Trupčević, Bases of standard modules for affine Lie algebras of type Cl(1), Comm. Algebra 46 (2018), 3663-3673.
MathSciNet
CrossRef
- G. Trupčević, Combinatorial bases of Feigin-Stoyanovsky's type subspaces of level 1 standard
 (l+1,ℂ)-modules, Comm. Algebra 38 (2010),
3913-3940.
(l+1,ℂ)-modules, Comm. Algebra 38 (2010),
3913-3940.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
 -module L(Λ) is a
-module L(Λ) is a  1-submodule of L(Λ) generated by
the highest-weight vector vΛ, where
1-submodule of L(Λ) generated by
the highest-weight vector vΛ, where  1 is a certain commutative subalgebra of
1 is a certain commutative subalgebra of  . Based on the description of basis of
W(Λ) for
. Based on the description of basis of
W(Λ) for  of type Cl(1), we give a presentation of this subspace in terms of generators and relations
W(Λ)≃ U(
of type Cl(1), we give a presentation of this subspace in terms of generators and relations
W(Λ)≃ U( 1-)/J.
1-)/J.
 r+1-modules,
Comm. Math. Phys. 264 (2006), 427-464.
r+1-modules,
Comm. Math. Phys. 264 (2006), 427-464.
 , Commun. Contemp. Math. 10 (2008), 47-79.
, Commun. Contemp. Math. 10 (2008), 47-79.
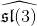 -modules, J. Pure
Appl. Algebra 219 (2015), 2300-2345.
-modules, J. Pure
Appl. Algebra 219 (2015), 2300-2345.
 (l+1,ℂ)-modules, Comm. Algebra 38 (2010),
3913-3940.
(l+1,ℂ)-modules, Comm. Algebra 38 (2010),
3913-3940.