Glasnik Matematicki, Vol. 53, No. 1 (2018), 97-113.
COMMUTATIVE OPERATORS FOR DOUBLE YANGIAN DY( )
)
Slaven Kožić
Department of Mathematics,
Faculty of Science,
University of Zagreb,
Bijenička cesta 30, 10000 Zagreb,
Croatia
e-mail: kslaven@math.hr
Abstract.
We derive explicit formulae for certain commutative vertex operators associated with Iohara's realization of the level 1 DY( )-modules.
As an application, we construct combinatorial bases for the corresponding principal subspaces and recover the classical character formulae. In the end, we discuss the underlying nonlocal vertex algebra theory.
)-modules.
As an application, we construct combinatorial bases for the corresponding principal subspaces and recover the classical character formulae. In the end, we discuss the underlying nonlocal vertex algebra theory.
2010 Mathematics Subject Classification.
17B37, 17B69.
Key words and phrases. Combinatorial basis, double Yangian, principal subspace, quantum vertex algebra.
Full text (PDF) (free access)
DOI: 10.3336/gm.53.1.07
References:
-
M. Butorac,
Combinatorial bases of principal subspaces for the affine Lie algebra of type B2(1),
J. Pure Appl. Algebra 218 (2014), 424-447.
MathSciNet
CrossRef
-
M. Butorac, Quasi-particle bases of principal subspaces for the affine Lie algebras of types
Bl(1) and Cl(1),
Glas. Mat. Ser. III 51(71) (2016), 59-108.
MathSciNet
CrossRef
-
M. Butorac,
Quasi-particle bases of principal subspaces for the affine Lie algebra of type G2(1),
Glas. Mat. Ser. III 52(72) (2017), 79-98.
MathSciNet
CrossRef
-
C. Calinescu, J. Lepowsky and A. Milas,
Vertex-algebraic structure of the principal subspaces of certain A(1)1-modules, I: level one case,
Internat. J. Math. 19, no. 01 (2008), 71-92.
MathSciNet
CrossRef
-
J. Ding and B. Feigin,
Commutative quantum current operators, semi-infinite construction and
functional models,
Represent. Theory 4 (2000), 330-341.
MathSciNet
CrossRef
-
V. G. Drinfeld,
Quantum groups, in: Proc. ICM Berkley (1986), American Mathematical Society, Providence, 1987, 798-820.
-
B. Enriquez and G. Felder,
A construction of Hopf algebra cocycles for the Yangian double DY(
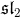 ),
J. Phys. A: Math. Gen. 31 (1998), 2401-2413.
),
J. Phys. A: Math. Gen. 31 (1998), 2401-2413.
MathSciNet
CrossRef
-
P. Etingof and D. Kazhdan,
Quantization of Lie bialgebras. V. Quantum vertex
operator algebras, Selecta Math. (N.S.) 6 (2000), 105-130.
MathSciNet
CrossRef
-
A. V. Stoyanovsky and B. L. Feigin,
Functional models of the representations of current algebras, and semi-infinite Schubert cells, Funktsional. Anal. i Prilozhen. 28 (1994), 68-90, 96;
translation in Funct. Anal. Appl. 28 (1994), 55-72.
MathSciNet
CrossRef
-
I. B. Frenkel and N. Jing,
Vertex representations of quantum affine algebras,
Proc. Natl. Acad. Sci. U.S.A. 85 (1988), 9373-9377.
CrossRef
MathSciNet
-
G. Georgiev,
Combinatorial constructions of modules for infinite-dimensional Lie algebras, I. Principal subspace,
J. Pure Appl. Algebra 112 (1996), 247-286.
MathSciNet
CrossRef
-
K. Iohara,
Bosonic representations of Yangian double DYh(
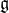 ) with
) with 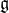 =
=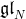 ,
,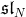 ,
J. Phys. A 29 (1996), 4593-4621.
,
J. Phys. A 29 (1996), 4593-4621.
MathSciNet
CrossRef
-
C. Kassel,
Quantum Groups, Springer-Verlag, New York, 1995.
MathSciNet
CrossRef
-
K. Kawasetsu,
The free generalized vertex algebras and generalized principal subspaces,
J. Algebra 444 (2015), 20-51.
MathSciNet
CrossRef
-
S. M. Khoroshkin and V. N. Tolstoy,
Yangian double,
Lett. Math. Phys. 36 (1996), 373-402.
MathSciNet
CrossRef
-
S. Kožić,
Principal subspaces for double Yangian DY(
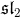 ),
J. Lie Theory 28 (2018), 673-694.
),
J. Lie Theory 28 (2018), 673-694.
MathSciNet
-
J. Lepowsky and M. Primc, Structure of the standard modules for the affine Lie algebra A1(1),
Contemp. Math. 46, Amer. Math. Soc., Providence, 1985.
MathSciNet
CrossRef
-
H.-S. Li,
Modules-at-infinity for quantum vertex algebras,
Commun. Math. Phys. 282 (2008), 819-864.
MathSciNet
CrossRef
-
H.-S. Li,
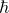 -adic quantum vertex algebras and their modules,
Commun. Math. Phys. 296 (2010), 475-523.
-adic quantum vertex algebras and their modules,
Commun. Math. Phys. 296 (2010), 475-523.
MathSciNet
CrossRef
-
M. Primc,
Vertex operator construction of standard modules for An(1),
Pacific J. Math 162 (1994), 143-187.
MathSciNet
CrossRef
-
M. Primc,
Basic Representations for classical affine Lie algebras,
J. Algebra 228 (2000), 1-50.
MathSciNet
CrossRef
-
C. Sadowski,
Presentations of the principal subspaces of the higher-level standard
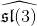 -modules,
J. Pure Appl. Algebra 219 (2015) 2300-2345.
-modules,
J. Pure Appl. Algebra 219 (2015) 2300-2345.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
 )
) )
) )-modules.
As an application, we construct combinatorial bases for the corresponding principal subspaces and recover the classical character formulae. In the end, we discuss the underlying nonlocal vertex algebra theory.
)-modules.
As an application, we construct combinatorial bases for the corresponding principal subspaces and recover the classical character formulae. In the end, we discuss the underlying nonlocal vertex algebra theory.
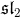 ),
J. Phys. A: Math. Gen. 31 (1998), 2401-2413.
),
J. Phys. A: Math. Gen. 31 (1998), 2401-2413.
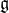 ) with
) with 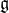 =
=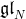 ,
,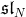 ,
J. Phys. A 29 (1996), 4593-4621.
,
J. Phys. A 29 (1996), 4593-4621.
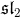 ),
J. Lie Theory 28 (2018), 673-694.
),
J. Lie Theory 28 (2018), 673-694.
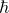 -adic quantum vertex algebras and their modules,
Commun. Math. Phys. 296 (2010), 475-523.
-adic quantum vertex algebras and their modules,
Commun. Math. Phys. 296 (2010), 475-523.
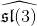 -modules,
J. Pure Appl. Algebra 219 (2015) 2300-2345.
-modules,
J. Pure Appl. Algebra 219 (2015) 2300-2345.