Glasnik Matematicki, Vol. 52, No. 2 (2017), 257-274.
REDUCIBILITY OF SOME GENERALIZED PRINCIPAL SERIES OF THE METAPLECTIC GROUP
Igor Ciganović
Department of Mathematics, University of Zagreb, 10 000 Zagreb, Croatia
e-mail: igor.ciganovic@math.hr
Abstract.
We determine reducibility of the representation of the metaplectic group induced from the tensor product of
an essentially square integrable representation attached to the Zelevinsky segment and a genuine cuspidal representation of the metaplectic group.
2010 Mathematics Subject Classification.
22D12, 22E50, 22D30, 11F85.
Key words and phrases. Metaplectic group, p-adic field, parabolic induction, Jacquet module, generalized principal series.
Full text (PDF) (free access)
DOI: 10.3336/gm.52.2.06
References:
-
I. N. Bernštein and A. V. Zelevinskii, Representations of
the group GL(n,F), where F is a local non-Archimedean field,
Uspehi Mat. Nauk 31 (1976), 5-70.
MathSciNet
-
I. N. Bernstein and A. V. Zelevinsky, Induced representations of
reductive p-adic groups. I, Ann. Sci. École Norm. Sup. (4)
10 (1977), 441-472.
MathSciNet
CrossRef
- I. Ciganović and N. Grbac, The Zelevinsky classification of unramified representations of the metaplectic group, J. Algebra 454 (2016), 357-399.
MathSciNet
CrossRef
-
W. T. Gan and G. Savin, Representations of metaplectic groups I:
epsilon dichotomy and local Langlands correspondence, Compos. Math.
148 (2012), 1655-1694.
MathSciNet
CrossRef
-
W. T. Gan and S. Takeda, A proof of the Howe duality conjecture, J. Amer. Math. Soc. 29 (2016), 473-493.
MathSciNet
CrossRef
-
D. Goldberg,
Reducibility of induced representation for Sp(2n) and SO(n),
Amer. J. Math. 116 (1994), 1101-1151.
MathSciNet
CrossRef
-
M. Hanzer and I. Matić,
The unitary dual of p-adic
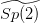 , Pacific J. Math. 248 (2010), 107-137.
, Pacific J. Math. 248 (2010), 107-137.
MathSciNet
CrossRef
-
M. Hanzer and G. Muić, Parabolic induction and Jacquet functors for metaplectic groups, J. Algebra 323 (2010), 241-260.
MathSciNet
CrossRef
-
M. Hanzer and G. Muić, Rank one reducibility for metaplectic groups via theta correspondence,
Canad. J. Math. 63 (2011), 591-615.
MathSciNet
CrossRef
-
S. S. Kudla, On the local theta-correspondence, Invent. Math.
83 (1986), 229-255.
MathSciNet
CrossRef
- I. Matić,
First occurrence indices of tempered representations of metaplectic groups,
Proc. Amer. Math. Soc. 144 (2016), 3157-3172.
MathSciNet
CrossRef
-
I. Matić, Strongly positive representations of metaplectic groups,
J. Algebra 334 (2011), 255-274.
MathSciNet
CrossRef
-
I. Matić, Jacquet modules of strongly positive representations of the metaplectic group
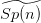 , Trans. Amer. Math. Soc. 365 (2013), 2755-2778.
, Trans. Amer. Math. Soc. 365 (2013), 2755-2778.
MathSciNet
CrossRef
-
I. Matić and M. Tadić, On Jacquet modules of representations of segment type, Manuscripta Math. 147 (2015), 437-476.
MathSciNet
CrossRef
-
C. Mœglin, Paquetes stables des séries discrètes accessibles par endoscopie tordue; leur paramètre de Langlands, in Automorphic forms and related geometry: assessing the Legacy of I. I. Piatetski-Shapiro, Contemp. Math. 614, Amer. Math. Soc., Providence, 2014, 295-336.
MathSciNet
CrossRef
-
C. Mœglin and M. Tadić,
Construction of discrete series for classical p-adic groups,
J. Amer. Math. Soc. 15 (2002), 715-786.
MathSciNet
CrossRef
-
C. Mœglin, M.-F. Vignéras and J.-L. Waldspurger,
Correspondances de Howe sur un corps p-adique, Lecture Notes in Mathematics
1291, Springer-Verlag, Berlin, 1987.
MathSciNet
CrossRef
-
R. Ranga Rao, On some explicit formulas in the theory of Weil
representation, Pacific J. Math. 157 (1993), 335-371.
MathSciNet
CrossRef
-
M. Tadić, On reducibility of parabolic induction, Israel J. Math.
107 (1998), 29-91.
MathSciNet
CrossRef
-
M. Tadić, Structure arising from induction and Jacquet modules of representations of classical p-adic groups, J. Algebra 177 (1995), 1-33.
MathSciNet
CrossRef
-
A. V. Zelevinsky, Induced representations of reductive p-adic groups.
II. On irreducible representations of GL(n), Ann. Sci. École
Norm. Sup. (4) 13 (1980), 165-210.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
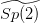 , Pacific J. Math. 248 (2010), 107-137.
, Pacific J. Math. 248 (2010), 107-137.
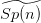 , Trans. Amer. Math. Soc. 365 (2013), 2755-2778.
, Trans. Amer. Math. Soc. 365 (2013), 2755-2778.