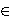 A(X) and some fixed integers m≥1,n≥1. In
this case there exists B
A(X) and some fixed integers m≥1,n≥1. In
this case there exists B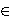 L (X), such that D(A)=AB-BA holds for all A
L (X), such that D(A)=AB-BA holds for all A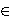 F(X), where F (X) denotes the ideal of all finite rank operators in L (X). Besides, D(Am)=AmB-BAm is fulfilled for all A
F(X), where F (X) denotes the ideal of all finite rank operators in L (X). Besides, D(Am)=AmB-BAm is fulfilled for all A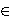 A(X).
A(X).
Abstract.
In this paper we prove the following result, which is related to a
classical result of Chernoff. Let X be a real or complex Banach space,
let A(X) be a standard operator algebra on X and let
L (X) be an algebra of all bounded linear operators on X. Suppose we have a
linear mapping D: A(X) → L (X) satisfying the relation D(Am+n)=D(Am)An+AmD(An) for all
A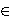 A(X) and some fixed integers m≥1,n≥1. In
this case there exists B
A(X) and some fixed integers m≥1,n≥1. In
this case there exists B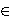 L (X), such that D(A)=AB-BA holds for all A
L (X), such that D(A)=AB-BA holds for all A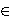 F(X), where F (X) denotes the ideal of all finite rank operators in L (X). Besides, D(Am)=AmB-BAm is fulfilled for all A
F(X), where F (X) denotes the ideal of all finite rank operators in L (X). Besides, D(Am)=AmB-BAm is fulfilled for all A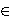 A(X).
A(X).
2010 Mathematics Subject Classification. 16N60, 39B05, 46K15.
Key words and phrases. Prime ring, semiprime ring, Banach space, standard operator algebra, derivation, Jordan derivation.
DOI: 10.3336/gm.52.2.04
References:
MathSciNet
CrossRef
MathSciNet
CrossRef
MathSciNet
CrossRef
MathSciNet
CrossRef
MathSciNet
CrossRef
MathSciNet
CrossRef
MathSciNet