Glasnik Matematicki, Vol. 51, No. 1 (2016), 59-108.
QUASI-PARTICLE BASES OF PRINCIPAL SUBSPACES FOR THE AFFINE LIE ALGEBRAS OF TYPES BL(1) AND CL(1)
Marijana Butorac
Department of Mathematics, University of Rijeka, Radmile Matejčić 2, 51 000 Rijeka, Croatia
e-mail: mbutorac@math.uniri.hr
Abstract.
Generalizing our earlier work, we construct quasi-particle bases of principal subspaces of standard module LXl(1)(kΛ0) and generalized Verma module NXl(1)(kΛ0) at level k≥ 1 in the case of affine Lie algebras of types Bl(1) and Cl(1). As a consequence, from quasi-particle bases, we obtain the graded dimensions of these subspaces.
2010 Mathematics Subject Classification.
17B67, 17B69, 05A19.
Key words and phrases. Affine Lie algebras, vertex operator algebras, principal subspaces, quasi-particle bases.
Full text (PDF) (free access)
DOI: 10.3336/gm.51.1.05
References:
- G. E. Andrews, The theory of partitions, Addison-Wesley, Reading, Mass.-London-Amsterdam, 1976.
MathSciNet
- E. Ardonne, R. Kedem and M. Stone, Fermionic characters of arbitrary highest-weight integrable
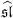 r+1-modules, Comm. Math. Phys. 264 (2006), 427-464.
r+1-modules, Comm. Math. Phys. 264 (2006), 427-464.
MathSciNet
CrossRef
- M. Butorac, Combinatorial bases of principal subspaces for the affine Lie algebra of type B2(1), J. Pure Appl. Algebra 218 (2014), 424-447.
MathSciNet
CrossRef
- C. Calinescu, Intertwining vertex operators and certain representations of
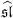 (n),
Commun. Contemp. Math. 10 (2008), 47-79.
(n),
Commun. Contemp. Math. 10 (2008), 47-79.
MathSciNet
CrossRef
- C. Calinescu, Principal subspaces of higher-level standard
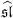 (3)-modules, J. Pure Appl. Algebra 210 (2007), 559-575.
(3)-modules, J. Pure Appl. Algebra 210 (2007), 559-575.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of the principal subspaces of
certain A(1)1-modules, I: level one case, Internat. J. Math. 19 (2008), 71-92.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of the principal subspaces of
certain A(1)1 -modules, II: higher-level case, J. Pure Appl. Algebra 212 (2008), 1928-1950.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of the principal subspaces of
level one modules for the untwisted affine Lie algebras of types A,D,E, J. Algebra 323 (2010), 167-192.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of principal subspaces of standard A2(2)-modules, I, Internat. J. Math. 25 (2014), 1450063, 44 pp.
MathSciNet
CrossRef
- S. Capparelli, J. Lepowsky and A. Milas,The Rogers-Ramanujan recursion and
intertwining operators, Commun. Contemp. Math. 5 (2003), 947-966.
MathSciNet
CrossRef
- S. Capparelli, J. Lepowsky and A. Milas, The Rogers-Selberg recursions, the Gordon-Andrews
identities and intertwining operators, Ramanujan J. 12 (2006), 379-397.
MathSciNet
CrossRef
- S. Dasmahapatra, R. Dedem, T. R. Klassen, B. McCoy and E. Melzer:
Quasi-particles, conformal field theory and q-series, Internat. J. Modern Phys. B7 (1993), 3617-3648.
MathSciNet
CrossRef
- C. Dong and J. Lepowsky, Generalized vertex algebras and relative vertex operators, Birkhäuser, Boston, 1993.
MathSciNet
CrossRef
- C. Dong, H. Li and G. Mason, Simple currents and extensions of vertex operator
algebras, Comm. Math. Phys. 180 (1996), 671-707.
MathSciNet
CrossRef
- E. Feigin, The PBW filtration, Represent. Theory 13 (2009), 165-181.
MathSciNet
CrossRef
- B. L. Feigin and A. V. Stoyanovsky, Functional models of the representations of
current algebras, and semi-infinite Schubert cells, (Russian) Funktsional. Anal. i
Prilozhen. 28 (1994), 68-90, 96; translation in Funct. Anal. Appl. 28 (1994),
55-72;
MathSciNet
CrossRef
- I. B. Frenkel, Y.-Z. Huang and J. Lepowsky, On axiomatic approaches to vertex operator algebras and modules, Mem. Amer. Math. Soc. 104, 1993.
MathSciNet
CrossRef
- B. Frenkel, J. Lepowsky and A. Meurman, Vertex operator algebras and the Monster,
Academic Press, Boston, 1988.
MathSciNet
- G. Georgiev, Combinatorial constructions of modules for infinite-dimensional Lie algebras,
I. Principal subspace, J. Pure Appl. Algebra 112 (1996), 247-286.
MathSciNet
CrossRef
- J. E. Humphreys, Introduction to Lie algebras and representation theory, Springer-Verlag, Berlin-Heidelberg-New York, 1972.
MathSciNet
- M. Jerković and M. Primc, Quasi-particle fermionic formulas for (k, 3) -admissible configurations, Cent. Eur. J. Math. 10 (2012), 703-721.
MathSciNet
CrossRef
- V. G. Kac, Infinite dimensional Lie algebras, 3rd ed., Cambridge University Press, Cambridge,
1990.
MathSciNet
CrossRef
- S. Kožić, Principal subspaces for quantum affine algebra Uq(A(1)n), J. Pure Appl. Algebra 218 (2014), 2119-2148.
MathSciNet
CrossRef
- S. Kožić and M. Primc, Quasi-particles in the principal picture of
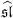 2 and Rogers-Ramanujan-type identities, preprint.
2 and Rogers-Ramanujan-type identities, preprint.
- J. Lepowsky and H.-S. Li, Introduction to vertex operator algebras and
their representations, Birkhäuser,
Boston, 2004.
MathSciNet
CrossRef
- J. Lepowsky and M. Primc, Structure of the standard modules for the affine Lie algebra
A(1)1, American Mathematical Society, Providence, 1985.
MathSciNet
CrossRef
- H.-S. Li, Local systems of vertex operators, vertex superalgebras and modules,
J. Pure Appl. Algebra 109 (1996), 143-195.
MathSciNet
CrossRef
- H.-S. Li, Certain extensions of vertex operator algebras of affine type, Commun.
Math. Phys. 217 (2001), 653-696.
MathSciNet
CrossRef
- A. Meurman and M. Primc, Annihilating fields of standard modules
of
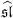 (2, C) and combinatorial identities, Mem. Amer. Math. Soc. 137, (1999), 652, 89 pp.
(2, C) and combinatorial identities, Mem. Amer. Math. Soc. 137, (1999), 652, 89 pp.
MathSciNet
CrossRef
- A. Milas and M. Penn, Lattice vertex algebras and combinatorial bases: general
case and W-algebras, New York J. Math. 18 (2012), 621-650.
MathSciNet
link
- C. Sadowski, Presentations of the principal subspaces of the higher-level standard
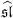 (3)-modules, J. Pure Appl. Algebra 219 (2015) 2300-2345.
(3)-modules, J. Pure Appl. Algebra 219 (2015) 2300-2345.
MathSciNet
CrossRef
- C. Sadowski, Principal subspaces of higher-level standard
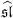 (n)-modules; Internat. J. Math. 26 (2015), 1550053, 35 pp.
(n)-modules; Internat. J. Math. 26 (2015), 1550053, 35 pp.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
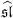 r+1-modules, Comm. Math. Phys. 264 (2006), 427-464.
r+1-modules, Comm. Math. Phys. 264 (2006), 427-464.
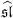 (n),
Commun. Contemp. Math. 10 (2008), 47-79.
(n),
Commun. Contemp. Math. 10 (2008), 47-79.
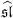 (3)-modules, J. Pure Appl. Algebra 210 (2007), 559-575.
(3)-modules, J. Pure Appl. Algebra 210 (2007), 559-575.
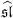 2 and Rogers-Ramanujan-type identities, preprint.
2 and Rogers-Ramanujan-type identities, preprint.
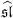 (2, C) and combinatorial identities, Mem. Amer. Math. Soc. 137, (1999), 652, 89 pp.
(2, C) and combinatorial identities, Mem. Amer. Math. Soc. 137, (1999), 652, 89 pp.
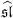 (3)-modules, J. Pure Appl. Algebra 219 (2015) 2300-2345.
(3)-modules, J. Pure Appl. Algebra 219 (2015) 2300-2345.
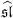 (n)-modules; Internat. J. Math. 26 (2015), 1550053, 35 pp.
(n)-modules; Internat. J. Math. 26 (2015), 1550053, 35 pp.