Glasnik Matematicki, Vol. 50, No. 2 (2015), 453-465.
CLASSIFICATION OF ROTATIONAL SURFACES IN PSEUDO-GALILEAN SPACE
Dae Won Yoon
Department of Mathematics Education and
RINS,
Gyeongsang National University, Jinju 660-701, South
Korea
e-mail: dwyoon@gnu.ac.kr
Abstract.
In the present paper, we study rotational surfaces in
the three dimensional pseudo-Galilean space G31 . Also, we
characterize rotational surfaces in G31 in terms of the
position vector field, Gauss map and Laplacian operator of the
second fundamental form on the surface.
2010 Mathematics Subject Classification.
53A35, 53C25.
Key words and phrases. Pseudo-Galilean space, rotational surface, second
fundamental form.
Full text (PDF) (free access)
DOI: 10.3336/gm.50.2.13
References:
- L. J. Alías, A. Ferrández and P. Lucas,
Surfaces in the 3-dimensional Lorentz-Minkowski space satisfying Δ x = A x +
B, Pacific J. Math. 156 (1992), 201-208.
MathSciNet
CrossRef
- L. J. Alías, A. Ferrández, P. Lucas and M. A.
Meroño, On the Gauss map of B-scrolls,
Tsukuba J. Math. 22 (1998), 371-377.
MathSciNet
- C. Baikoussis and D. E. Blair,
On the Gauss map of ruled surfaces,
Glasgow Math. J. 34 (1992), 355-359.
MathSciNet
CrossRef
- S. M. Choi,
On the Gauss map of surfaces of
revolution in a 3-dimensional Minkowski space,
Tsukuba J. Math.
19 (1995), 351-367.
MathSciNet
- M. Choi, Y. H. Kim and D. W. Yoon,
Some classification of surfaces of
revolution in Minkowski 3-space,
J. Geom. 104 (2013), 85-106.
MathSciNet
CrossRef
- F. Dillen, J. Pas and L. Vertraelen,
On the Gauss map of surfaces of revolution,
Bull. Inst. Math. Acad. Sinica 18 (1990), 239-246.
MathSciNet
- B. Divjak and Ž. Milin Šipuš,
Some special surface in the pseudo-Galilean space,
Acta Math. Hungar. 118 (2008), 209-226.
MathSciNet
CrossRef
- O. J. Garay,
An extension of Takahashi's theorem,
Geom. Dedicata 34 (1990), 105-112.
MathSciNet
CrossRef
- G. Kaimakamis and B, Papantoniou,
Surfaces of revolution in the 3-dimensional Lorentz-Minkowski
space satisfying ΔII
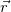 =A
=A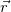 ,
J. Geom. 81 (2004), 81-92.
,
J. Geom. 81 (2004), 81-92.
MathSciNet
CrossRef
- G. Kaimakamis, B. Papantoniou and K.
Petoumenos,
Surfaces of revolution in the 3-dimensional Lorentz-Minkowski space E31
satisfying ΔIII
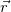 =A
=A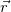 ,
Bull. Greek Math. Soc. 50 (2005), 75-90.
,
Bull. Greek Math. Soc. 50 (2005), 75-90.
MathSciNet
- Y. H. Kim, C. W. Lee and D. W. Yoon,
On the Gauss map of surfaces of revolution without parabolic points,
Bull. Korean Math. Soc. 46 (2009), 1141-1149.
MathSciNet
CrossRef
- C. W. Lee, Y. H. Kim and D. W. Yoon,
Ruled surfaces of non-degenerate third fundamental forms in Minkowski 3-spaces,
Appl. Math. Comput. 216 (2010), 3200-3208.
MathSciNet
CrossRef
- E. Molnár,
The projective interpretation of the eight 3-dimensional homogeneous geometries,
Beiträge Algebra Geom. 38 (1997), 261-288.
MathSciNet
- B. Senoussi and M. Bekkar,
Helicoidal surfaces in the three-dimensional Lorentz-Minkowski space satisfying ΔII r=Ar,
Kyushu J. Math. 67 (2013), 327-338.
MathSciNet
CrossRef
- B. Senoussi and M. Bekkar,
Helicoidal surfaces in the 3-dimensional Lorentz-Minkowski
space E31 satisfying ΔIII r=Ar, Tsukuba J.
Math. 37 (2013), 339-353.
MathSciNet
CrossRef
- Ž. Milin Šipuš and B. Divjak,
Surfaces of constant curvature in the pseudo-Galilean space,
Int. J. Math. Math. Sci. 2012, Art. ID 375264, 28 pp.
MathSciNet
- T. Takahashi,
Minimal immersions of Riemannian manifolds,
J. Math. Soc. Japan 18 (1966), 380-385.
MathSciNet
CrossRef
- D. W. Yoon,
On the Gauss map of translation surfaces in Minkowski
3-space, Taiwanese J. Math. 6 (2002), 389-398.
MathSciNet
- D. W. Yoon,
Surfaces of revolution in the three dimensional pseudo-Galilean space,
Glas. Mat. Ser. III 48(68) (2013), 415-428.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
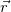 =A
=A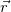 ,
J. Geom. 81 (2004), 81-92.
,
J. Geom. 81 (2004), 81-92.
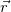 =A
=A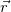 ,
Bull. Greek Math. Soc. 50 (2005), 75-90.
,
Bull. Greek Math. Soc. 50 (2005), 75-90.